DCM Advanced Part II Will Penny Klaas Stephan

DCM Advanced, Part II Will Penny (Klaas Stephan) Wellcome Trust Centre for Neuroimaging Institute of Neurology University College London SPM Course 2014 @ FIL

Overview • Extended DCM for f. MRI: nonlinear, two-state, stochastic • Embedding computational models in DCMs • Clinical Applications

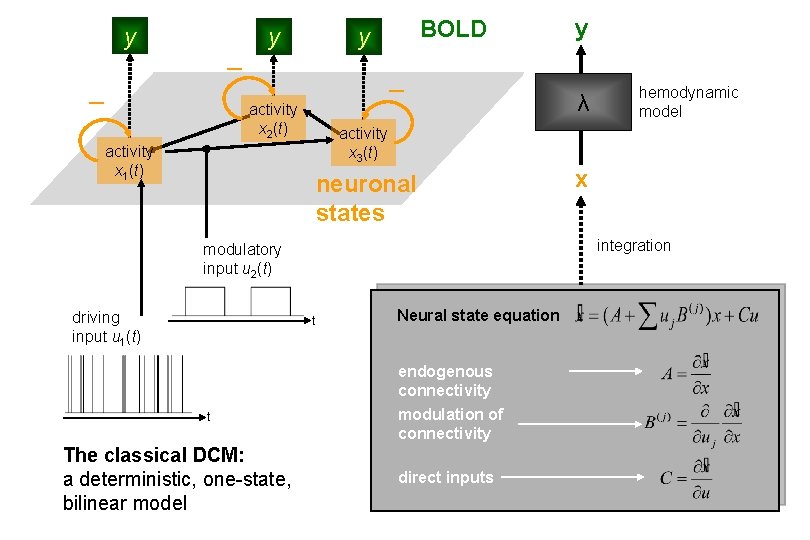
y y BOLD y activity x 2(t) neuronal states t Neural state equation endogenous connectivity The classical DCM: a deterministic, one-state, bilinear model hemodynamic model x integration modulatory input u 2(t) t λ activity x 3(t) activity x 1(t) driving input u 1(t) y modulation of connectivity direct inputs

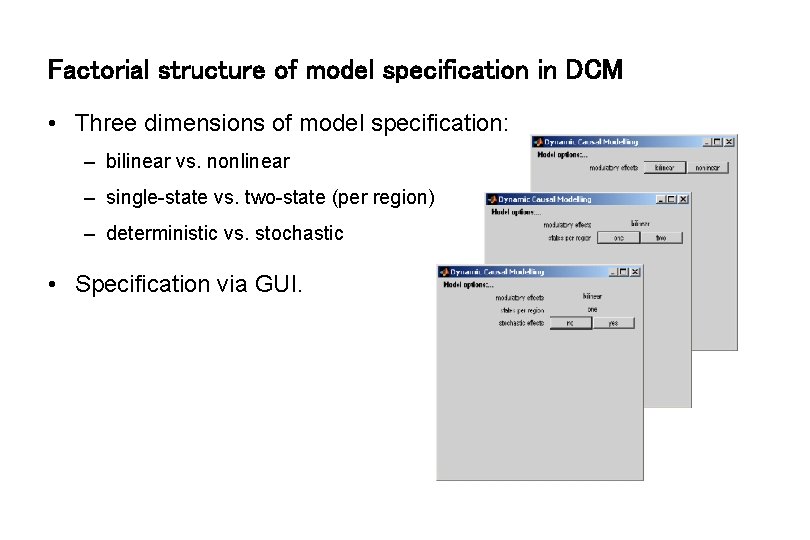
Factorial structure of model specification in DCM • Three dimensions of model specification: – bilinear vs. nonlinear – single-state vs. two-state (per region) – deterministic vs. stochastic • Specification via GUI.

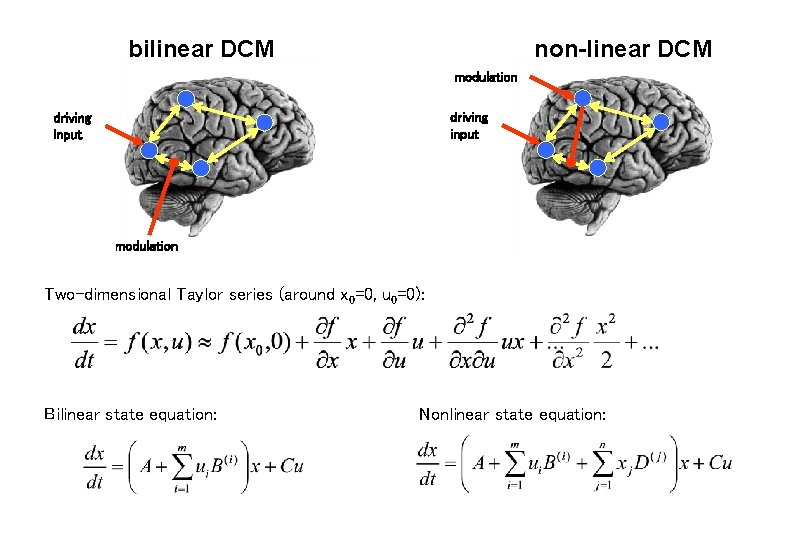
bilinear DCM non-linear DCM modulation driving input modulation Two-dimensional Taylor series (around x 0=0, u 0=0): Bilinear state equation: Nonlinear state equation:

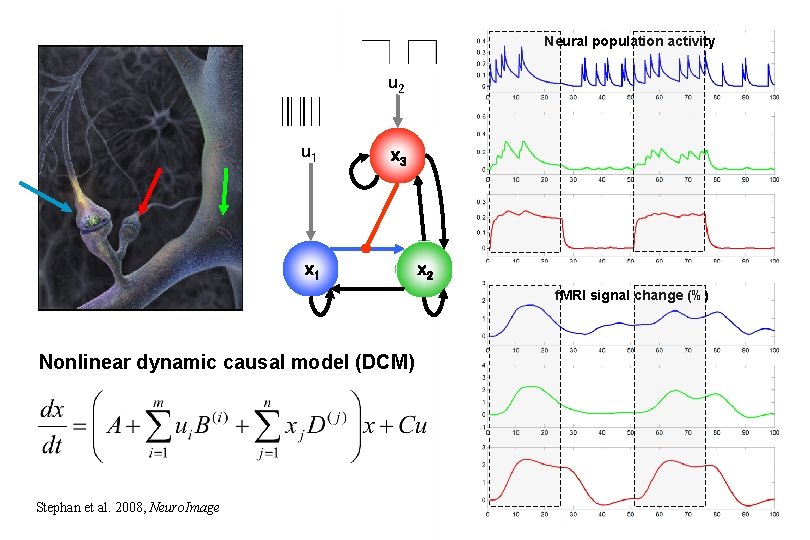
Neural population activity u 2 u 1 x 3 x 1 x 2 f. MRI signal change (%) Nonlinear dynamic causal model (DCM) Stephan et al. 2008, Neuro. Image

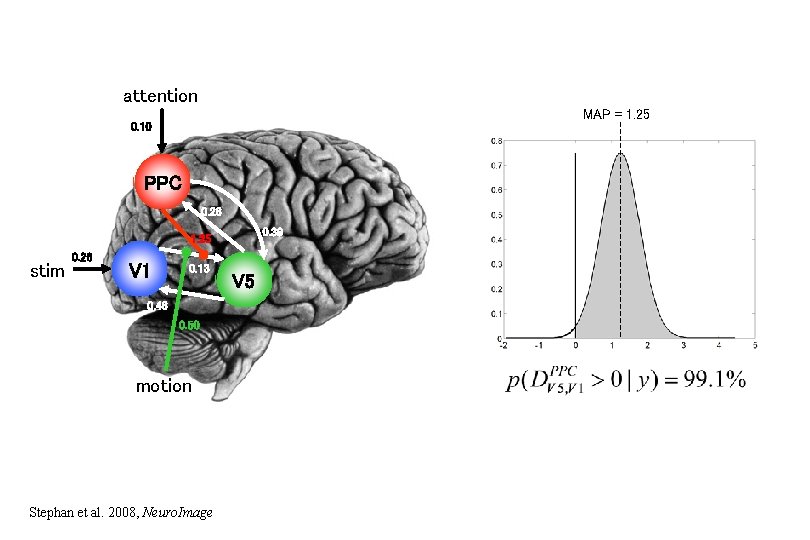
attention MAP = 1. 25 0. 10 PPC 0. 26 0. 39 1. 25 stim 0. 26 V 1 0. 13 0. 46 0. 50 motion Stephan et al. 2008, Neuro. Image V 5

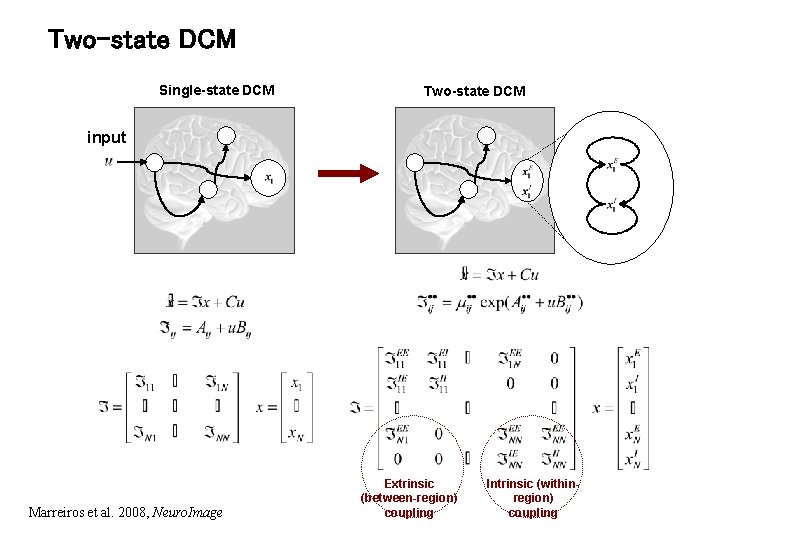
Two-state DCM Single-state DCM Two-state DCM input Marreiros et al. 2008, Neuro. Image Extrinsic (between-region) coupling Intrinsic (withinregion) coupling

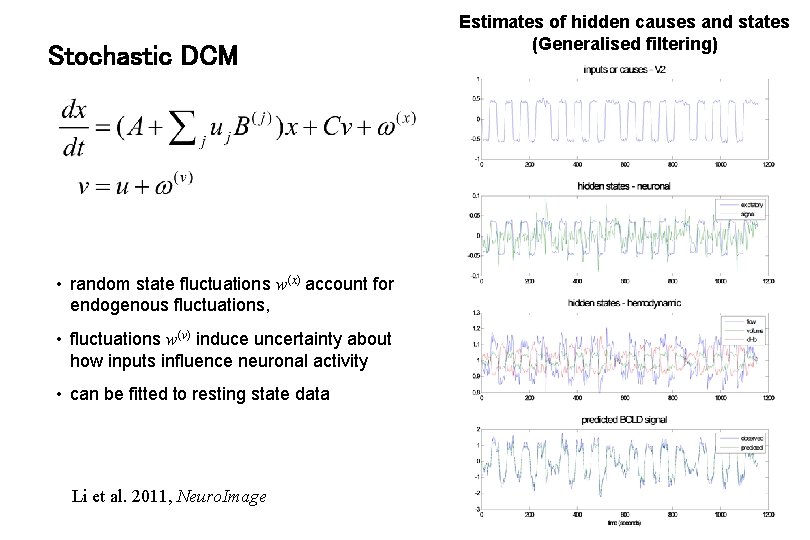
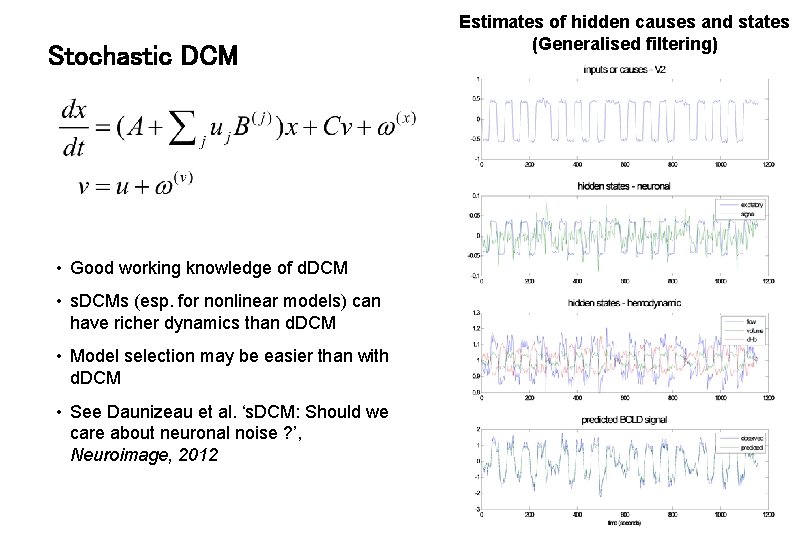
Stochastic DCM • random state fluctuations w(x) account for endogenous fluctuations, • fluctuations w(v) induce uncertainty about how inputs influence neuronal activity • can be fitted to resting state data Li et al. 2011, Neuro. Image Estimates of hidden causes and states (Generalised filtering)

Stochastic DCM • Good working knowledge of d. DCM • s. DCMs (esp. for nonlinear models) can have richer dynamics than d. DCM • Model selection may be easier than with d. DCM • See Daunizeau et al. ‘s. DCM: Should we care about neuronal noise ? ’, Neuroimage, 2012 Estimates of hidden causes and states (Generalised filtering)

Overview • Extended DCM for f. MRI: nonlinear, two-state, stochastic • Embedding computational models in DCMs • Clinical Applications

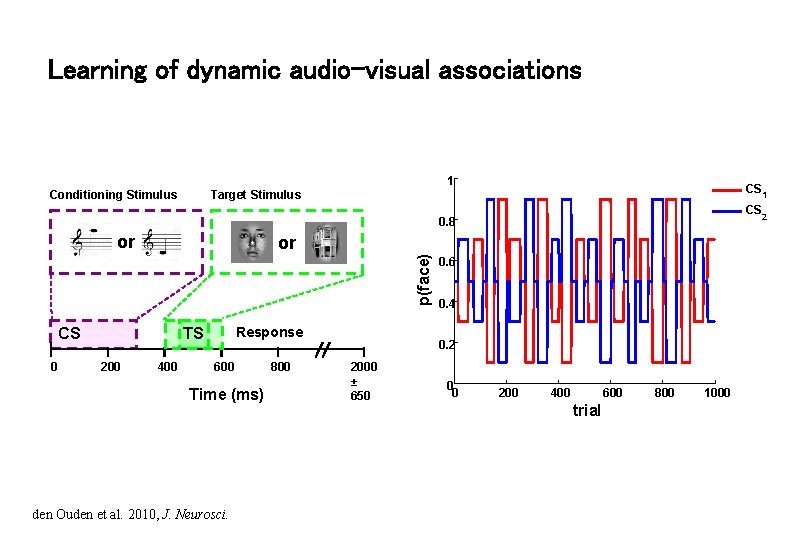
Learning of dynamic audio-visual associations 1 Conditioning Stimulus CS 1 Target Stimulus CS 2 0. 8 or p(face) or CS 0 Response TS 200 400 600 Time (ms) den Ouden et al. 2010, J. Neurosci. 800 0. 6 0. 4 0. 2 2000 ± 650 0 0 200 400 600 trial 800 1000

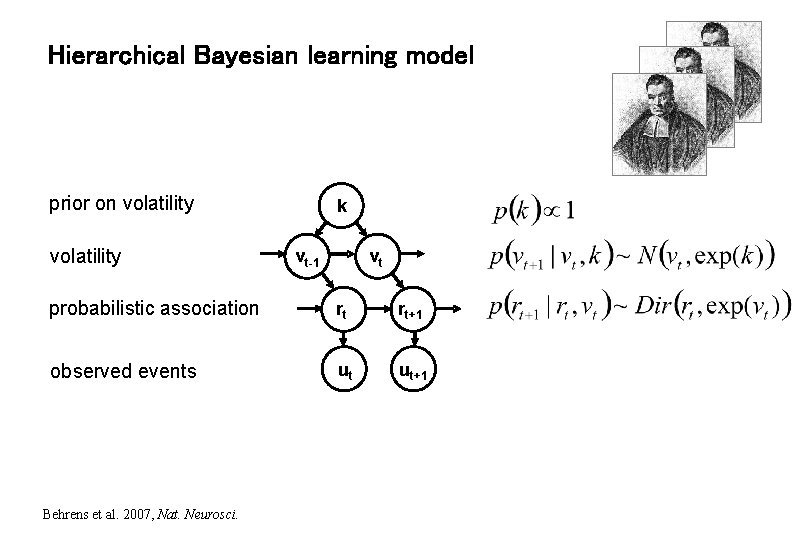
Hierarchical Bayesian learning model prior on volatility k vt-1 vt probabilistic association rt rt+1 observed events ut ut+1 Behrens et al. 2007, Nat. Neurosci.

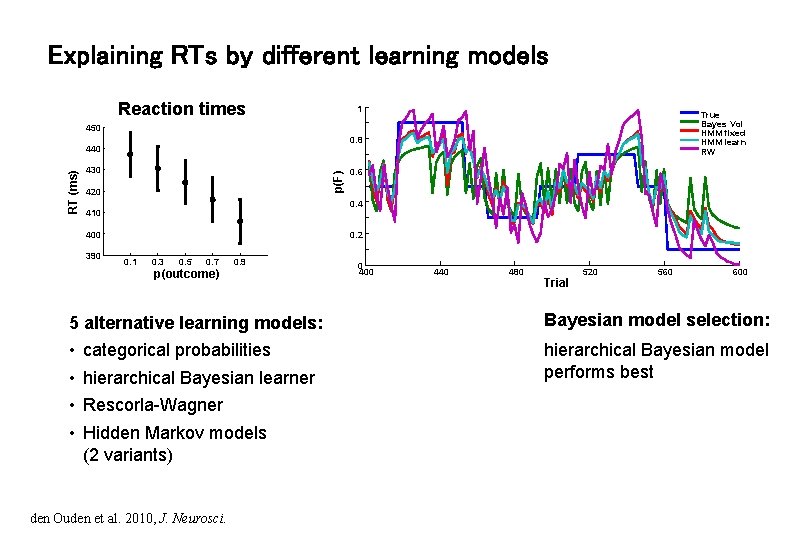
Explaining RTs by different learning models Reaction times 1 True Bayes Vol HMM fixed HMM learn RW 450 0. 8 430 p(F) RT (ms) 440 420 0. 4 410 400 390 0. 6 0. 2 0. 1 0. 3 0. 5 0. 7 0. 9 p(outcome) 0 400 440 480 Trial 520 560 600 5 alternative learning models: Bayesian model selection: • • hierarchical Bayesian model performs best categorical probabilities hierarchical Bayesian learner Rescorla-Wagner Hidden Markov models (2 variants) den Ouden et al. 2010, J. Neurosci.

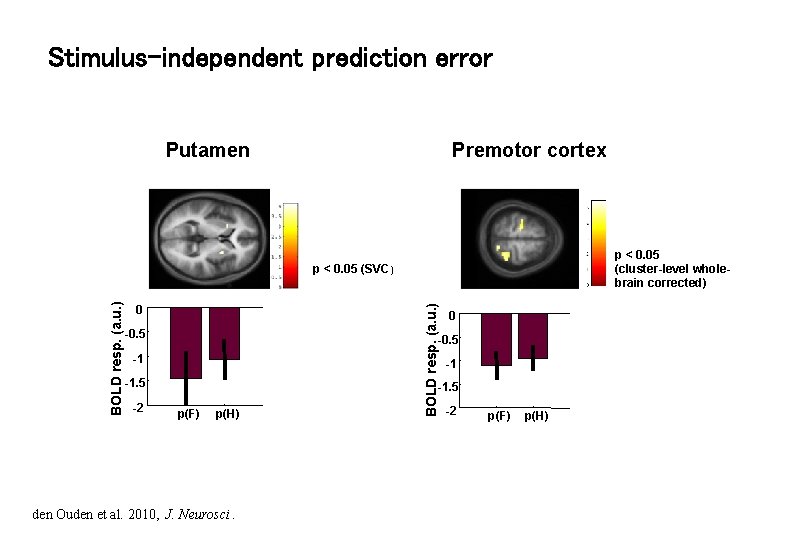
Stimulus-independent prediction error Putamen Premotor cortex p < 0. 05 (cluster-level wholebrain corrected) 0 -0. 5 -1 -1. 5 -2 BOLD resp. (a. u. ) p < 0. 05 (SVC) -1 -1. 5 p(F) p(H) den Ouden et al. 2010, J. Neurosci. -2 p(F) p(H)

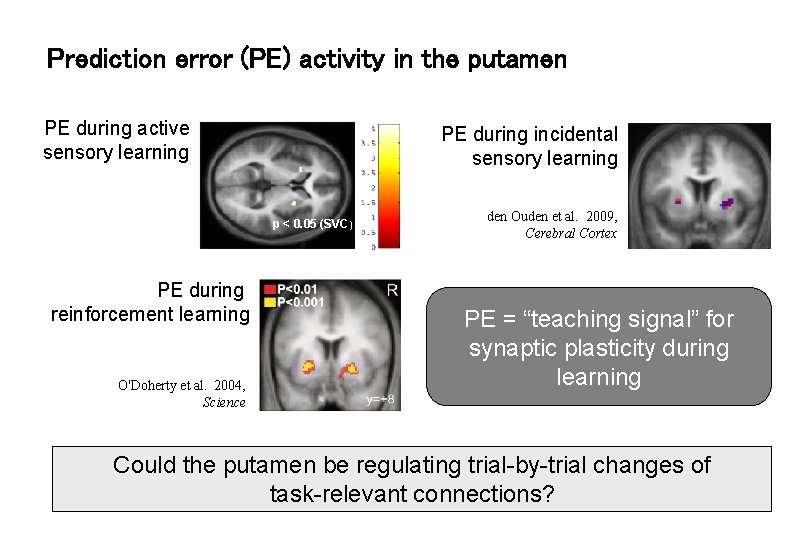
Prediction error (PE) activity in the putamen PE during active sensory learning PE during incidental sensory learning p < 0. 05 (SVC) PE during reinforcement learning O'Doherty et al. 2004, Science den Ouden et al. 2009, Cerebral Cortex PE = “teaching signal” for synaptic plasticity during learning Could the putamen be regulating trial-by-trial changes of task-relevant connections?

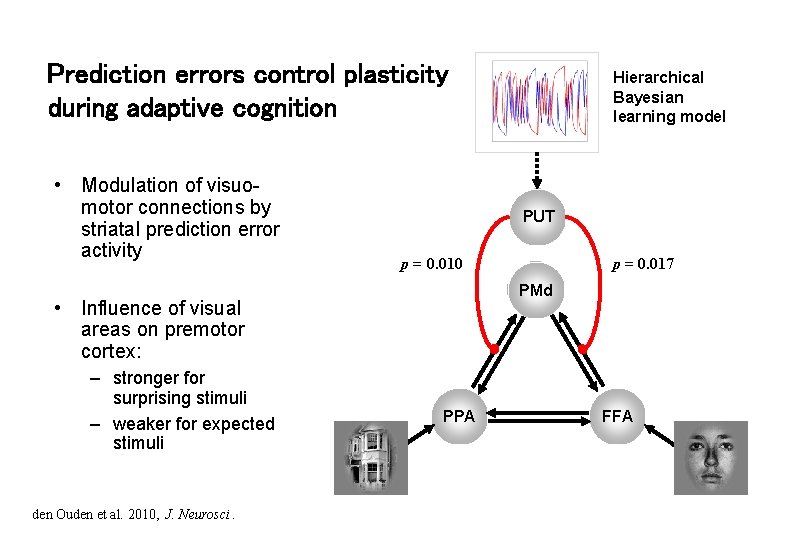
Prediction errors control plasticity during adaptive cognition • Modulation of visuomotor connections by striatal prediction error activity PUT den Ouden et al. 2010, J. Neurosci. p = 0. 017 p = 0. 010 PMd • Influence of visual areas on premotor cortex: – stronger for surprising stimuli – weaker for expected stimuli Hierarchical Bayesian learning model PPA FFA

Overview • Extended DCM for f. MRI: nonlinear, two-state, stochastic • Embedding computational models in DCMs • Clinical Applications

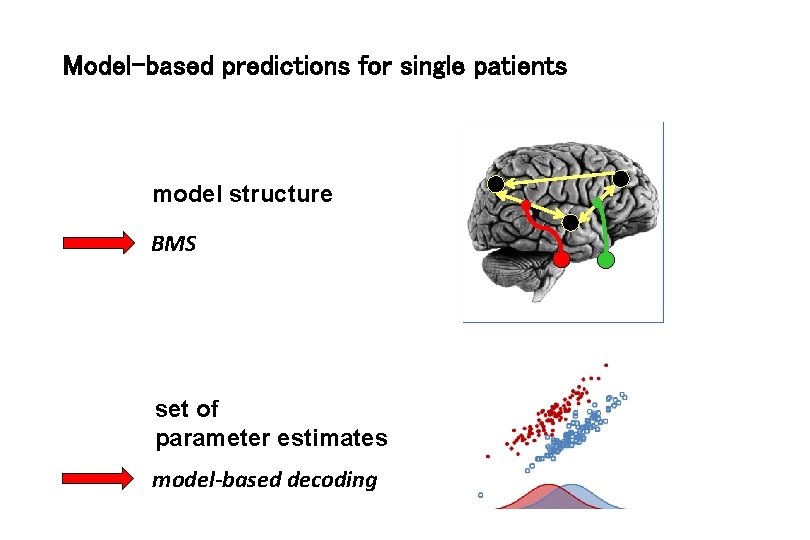
Model-based predictions for single patients model structure BMS set of parameter estimates model-based decoding

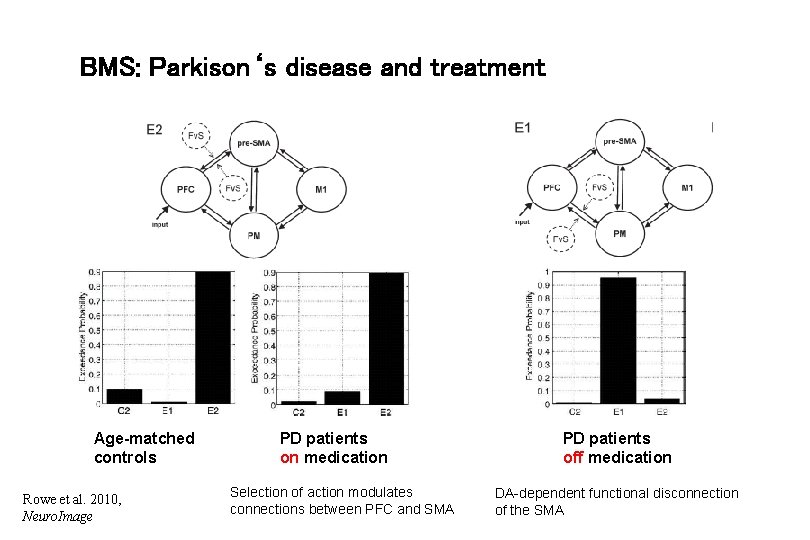
BMS: Parkison‘s disease and treatment Age-matched controls Rowe et al. 2010, Neuro. Image PD patients on medication Selection of action modulates connections between PFC and SMA PD patients off medication DA-dependent functional disconnection of the SMA

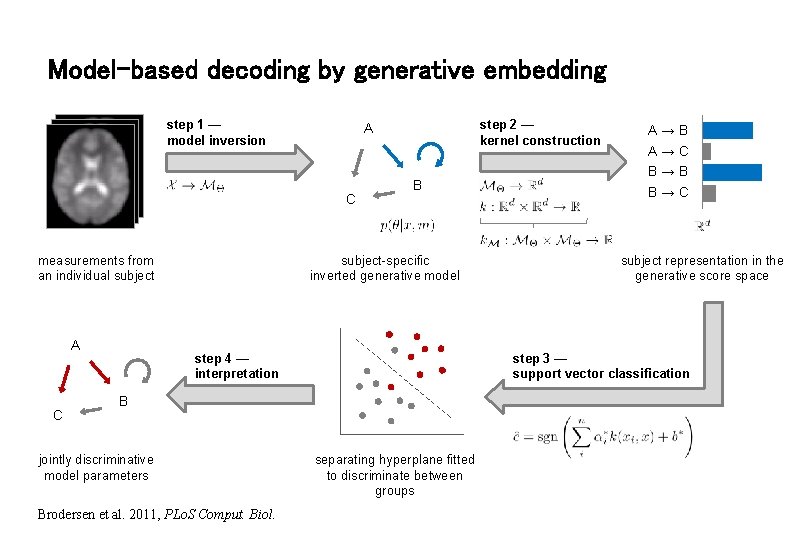
Model-based decoding by generative embedding step 1 — model inversion C measurements from an individual subject A C step 2 — kernel construction A B subject-specific inverted generative model B Brodersen et al. 2011, PLo. S Comput. Biol. subject representation in the generative score space step 3 — support vector classification step 4 — interpretation jointly discriminative model parameters A→B A→C B→B B→C separating hyperplane fitted to discriminate between groups

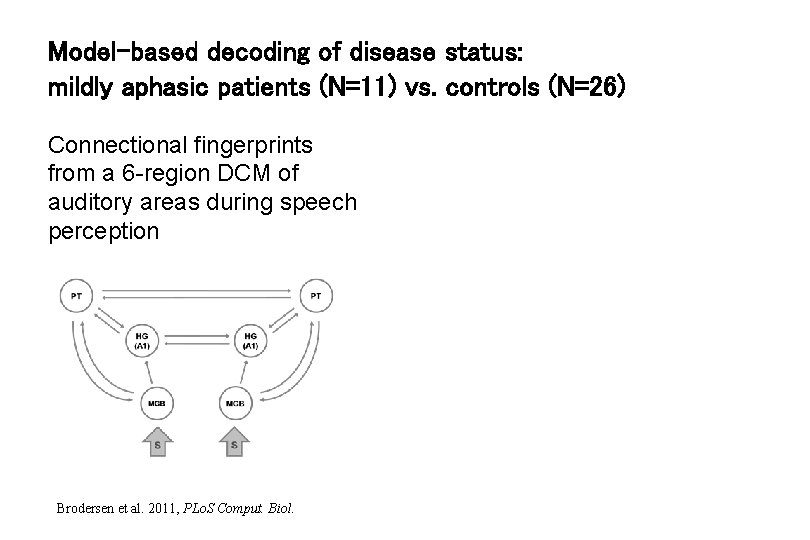
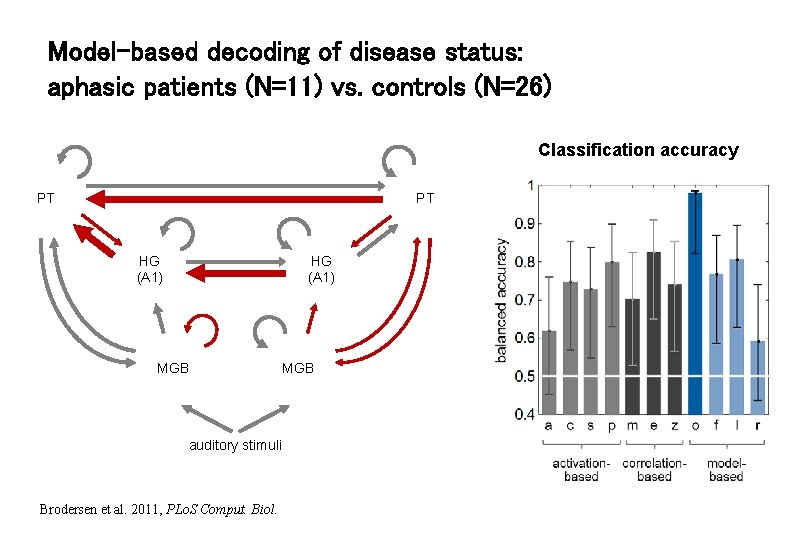
Model-based decoding of disease status: mildly aphasic patients (N=11) vs. controls (N=26) Connectional fingerprints from a 6 -region DCM of auditory areas during speech perception Brodersen et al. 2011, PLo. S Comput. Biol.

Model-based decoding of disease status: aphasic patients (N=11) vs. controls (N=26) Classification accuracy PT PT HG (A 1) MGB auditory stimuli Brodersen et al. 2011, PLo. S Comput. Biol. MGB

Multivariate searchlight classification analysis Generative embedding using DCM

Summary • Model Selection • Extended DCM for f. MRI: nonlinear, two-state, stochastic • Embedding computational models in DCMs • Clinical Applications