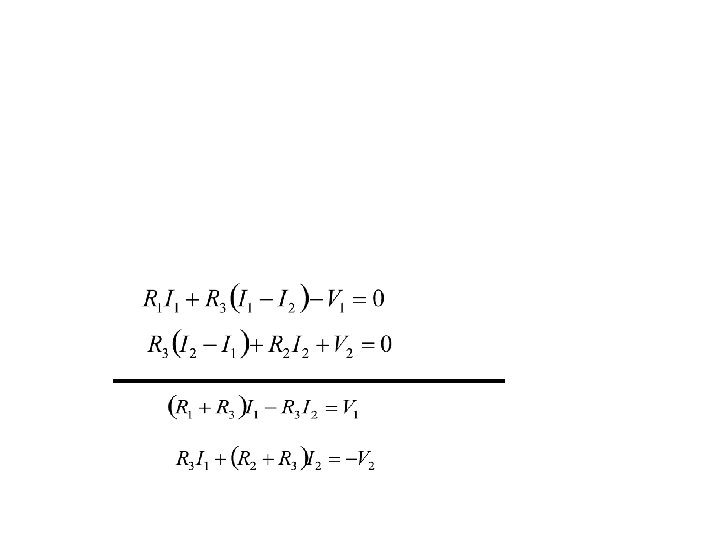DC circuits and methods of circuits analysis Circuits

![Voltage source - V [V] • Ideal source Constant output voltage, internal resistance equals Voltage source - V [V] • Ideal source Constant output voltage, internal resistance equals](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-2.jpg)
![Current source - I [A] • Ideal source Constant output current, internal resistance equals Current source - I [A] • Ideal source Constant output current, internal resistance equals](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-3.jpg)
![Resistance - R [ ] • Coductance G=1/R [S] • Ideal resistor linear R Resistance - R [ ] • Coductance G=1/R [S] • Ideal resistor linear R](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-4.jpg)










![Inductors Details for instalation and ordering L [H], IMAX [A] Lower units 1 µH Inductors Details for instalation and ordering L [H], IMAX [A] Lower units 1 µH](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-18.jpg)












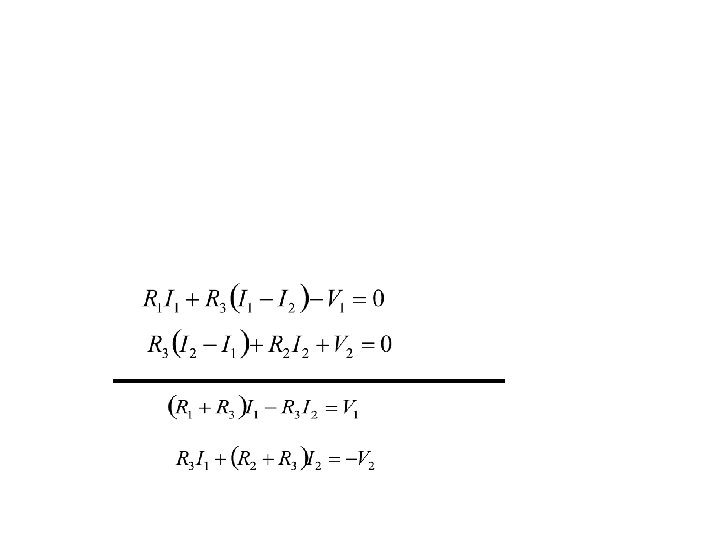
- Slides: 32

DC circuits and methods of circuits analysis • Circuits elements: • • • Voltage source Current source Resistors Capacitors Inductors
![Voltage source V V Ideal source Constant output voltage internal resistance equals Voltage source - V [V] • Ideal source Constant output voltage, internal resistance equals](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-2.jpg)
Voltage source - V [V] • Ideal source Constant output voltage, internal resistance equals to zero • Real source Output voltage depends on various conditions. Dependence may be linear (battery) on non-linear
![Current source I A Ideal source Constant output current internal resistance equals Current source - I [A] • Ideal source Constant output current, internal resistance equals](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-3.jpg)
Current source - I [A] • Ideal source Constant output current, internal resistance equals to infinity • Real source Output current depends on various conditions. Dependence may be linear on non-linear (Usually electronic sources)
![Resistance R Coductance G1R S Ideal resistor linear R Resistance - R [ ] • Coductance G=1/R [S] • Ideal resistor linear R](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-4.jpg)
Resistance - R [ ] • Coductance G=1/R [S] • Ideal resistor linear R = const. V= I. R • Real resistor non-linear (electric bulb, PN junction)

Resistance (2) • Resistors in series R = R 1 + R 2 • Resistors in parallel R = R 1 // R 2 = (R 1. R 2) / (R 1 + R 2) • Voltage divider U 2 = U. R 2 /(R 1 + R 2) potential divider (‘pot’)

Passive electronic parts • Resistors feature electrical resistivity R dimensioning according maximal dissipation power (loses) Pmax • Capacitors feature capacity C dimensioning according maximal granted voltage Vmax • Inductors feature inductivity L dimensioning according maximal granted current Imax

Resistors • Feature: resistivity • r = R = const. • nonreversible el. energy transfer to heat • • • Data: R [Ω], P [W] • Description: Ω → J, R 4, 7 Ω → 4 R 7 • kΩ → k 68 kΩ → 68 k • MΩ → M 2. 2 MΩ → 2 M 2 • 0, 15 MΩ → M 15 • 47 k/0, 125 W 3 R 3/ 5 W

Resistors color codings color num ber tolerance Meaning Blacká 0 Brown 1 ± 1% Strip 4 strips 5 strips Red 2 ± 2% 1 first digit Orange 3 2 second digit Yelow 4 3 exponent 10 x third digit Green 5 ± 0, 5 % 4 tolerance exponent 10 x Blue 6 ± 0, 25 % 5 violet 7 ± 0, 1 % grey 8 white 9 gold -1 ± 5% silver -2 ± 10 % no color ± 20 % tolerance First strip is near to edge than last If tolerance is ± 20 %, the 4. strip miss

Resistors Material • Carbon – non stable, temperature dependent • Metalised - stable, precise • Wired more power dissipation > 5 W

Resistors Potentiometer variable resistor Potentiometr adjustable by hand Potentiometer adjustable by tool

Resistors

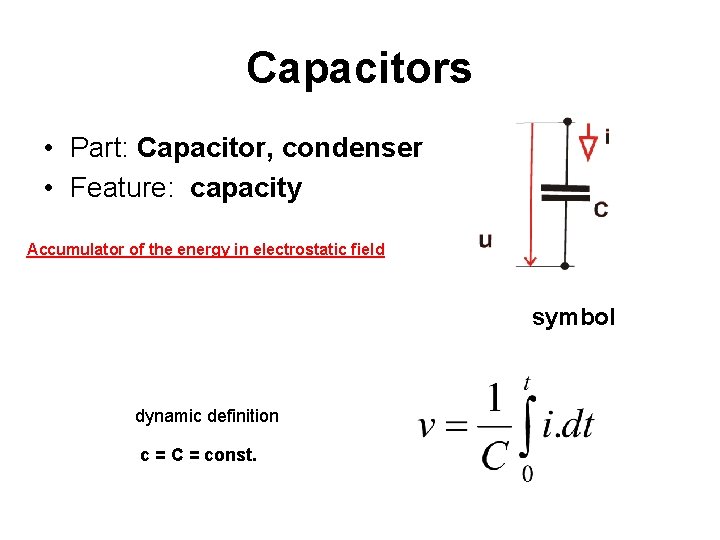
Capacitors • Part: Capacitor, condenser • Feature: capacity Accumulator of the energy in electrostatic field symbol dynamic definition c = C = const.

Capacitors static definition power definition For calculation should be used SI system only! : unit: 1 F (Farrad) dimension: [A. s/V]

Capacitors Description: • p. F → J, R • 103 p. F → k , n • 106 p. F → M 4, 7 p. F → 4 R 7 68 000 p. F → 68 k 3, 3 µF → 3 M 3 • 109 p. F → G 200 µF → 200 M Number code: number, exponent in p. F eg. : 474 → 470 000 p. F → 470 k → M 47 ± 20%

Capacitors

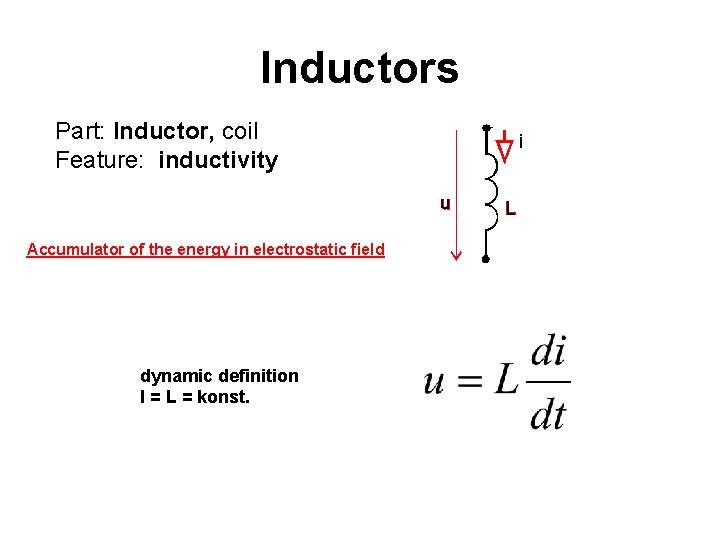
Inductors Part: Inductor, coil Feature: inductivity Accumulator of the energy in electrostatic field dynamic definition l = L = konst.

Inductors static definition power definition For calculation should be used SI system only! : unit: 1 H (Henry) dimension: [V. s/A]
![Inductors Details for instalation and ordering L H IMAX A Lower units 1 µH Inductors Details for instalation and ordering L [H], IMAX [A] Lower units 1 µH](https://slidetodoc.com/presentation_image_h2/51570a9552999967c319c07e8abf9788/image-18.jpg)
Inductors Details for instalation and ordering L [H], IMAX [A] Lower units 1 µH = 10 -3 m. H = 10 -6 H ---------It use in electronic not very often. See next semestr

Ohm’s and Kirchhoff’s laws • Ohm’s law I=U/R • 1 st Kirchhoff’s law (KCL) I = 0 At any node of a network, at every instant of time, the algebraic sum of the currents at the node is zero • 2 nd Kirchhoff’s law (KVL) U = 0 The algebraic sum of the voltages across all the components around any loop of circuits is zero

Nodal analysis (for most circuits the best way) • Uses 1 st K. law – Chose reference node – Label all other voltage nodes – Eliminate nodes with fixed voltage by source of emf – At each node apply 1 st K. law – Solve the equations

Mesh analysis • Uses 2 nd K. law – Find independent meshs – Eliminate meshs with fixed current source – Across each mesh apply 2 nd K. law – Solve the equations

Thevenin equialent circuit for linear circuit As far as any load connected across its output terminals is concerned, a linear circuits consisting of voltage sources, current sources and resistances is equivalent to an ideal voltage source VT in series with a resistance RT. The value of the voltage source is equal to the open circuit voltage of the linear circuit. The resistance which would be measured between the output terminals if the load were removed and all sources were replaced by their internal resistances.

Norton equialent circuit for linear circuit As far as any load connected across its output terminals is concerned, a linear circuits consisting of voltage sources, current sources and resistances is equivalent to an ideal current source IN in parallel with a resistance RN. The value of the current source is equal to the short circuit voltage of the linear circuit. The value of the resistance is equal to the resistance measured between the output terminals if the load were removed and all sources were replaced by their internal resistances.

Principle of superposition • The principle of superposition is that, in a linear network, the contribution of each source to the output voltage or current can be worked out independently of all other sources, and the various contribution then added together to give the net output voltage or current.

Example

Methods of electrical circuits analysis: • Node Voltage Method • Mesh Current Method Σii = 0 , ΣIi = 0 Σvi = 0 , ΣVi = 0 • Thevenin and Norton Eq. Cirtuits • Principle of Superposition • --- and other 15 methods

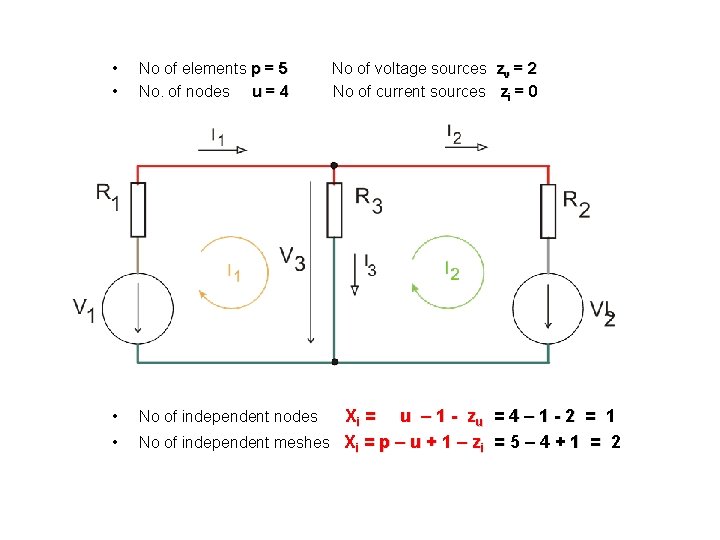
Topology and Number of Lineary Independent Equations No. of elements No. of nodes p u zv No. of current sources zi No. of voltage sources

• • No of elements p = 5 No. of nodes u = 4 • No of independent nodes • No of voltage sources zv = 2 No of current sources zi = 0 Xi = u – 1 - z u = 4 – 1 - 2 = 1 No of independent meshes Xi = p – u + 1 – zi = 5 – 4 + 1 = 2

Node Voltage Analysis Method 1. Select a reference node (usually ground). All other node voltages will be referenced to this node. 2. Define remaining n-1 node voltages as the independent variables. 3. Apply KCL at each of the n-1 nodes, expressing each current in terms of the adjacent node voltages 4. Solve the linear system of n-1 equations in n-1 unknowns


Mesh Current Analysis Method 1. Define each mesh current consistently. We shall define each current clockwise, for convenience 2. Apply KVL around each mesh, expressing each voltage in terms of one or more mesh currents 3. Solve the resulting linear system of equations with mesh currents as the independent variables