DC circuit theory Learning outcomes explain the behaviour

DC circuit theory

Learning outcomes • explain the behaviour of DC circuits using concepts of EMF, internal resistance of power sources and potential dividers • give a microscopic description of resistance in a wire • define and use concepts of resistivity and conductance • state Kirchhoff’s laws and use them to analyse DC circuits • define capacitance and solve DC circuit problems involving capacitors, including energy stored • carry out related practical work (using voltmeter, ammeter, multimeter, micrometer)

Teaching challenges It is always advisable to revisit concepts introduced at KS 3 and GCSE level, to identify misconceptions about electricity and (try to) correct them. In pairs: Make a spidergram showing key concepts related to electric circuits, and relationships between them.

EMF and potential difference A-level: A battery maintains an electric field through the circuit. This enables it to do work on charges wherever there is a potential difference e. g. in a filament. Electromotive force is the energy supplied per unit charge. (work done on each coulomb of charge) Potential difference (p. d. ) is the energy transferred per unit charge between 2 points in a circuit. (work done by each coulomb of charge) Unit (for both) is the volt = joule/coulomb

Resistor networks Resistors in series V = V 1+ V 2 [conservation of energy] IR = IR 1 + IR 2 R = R 1 + R 2 R is always larger than any of R 1, R 2 etc Resistors in parallel I = I 1 + I 2 [conservation of charge] V/R = V/R 1 + V/R 2 1/R = 1/R 1 + 1/R 2 R is always smaller than any of R 1, R 2 etc

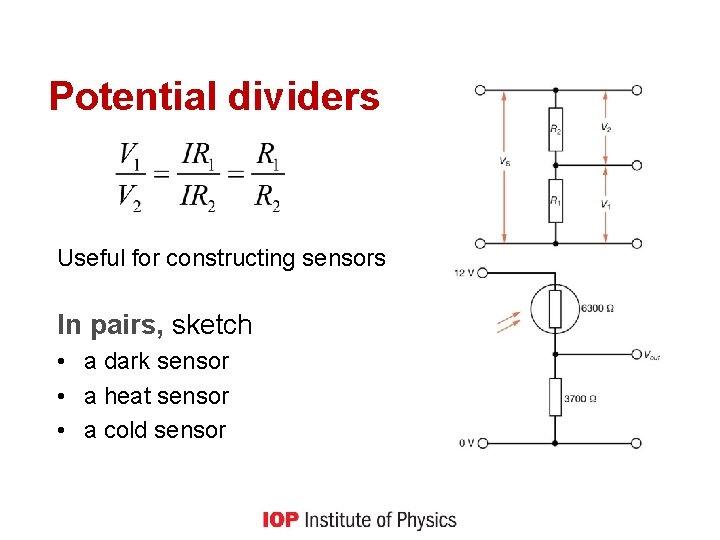
Potential dividers Useful for constructing sensors In pairs, sketch • a dark sensor • a heat sensor • a cold sensor

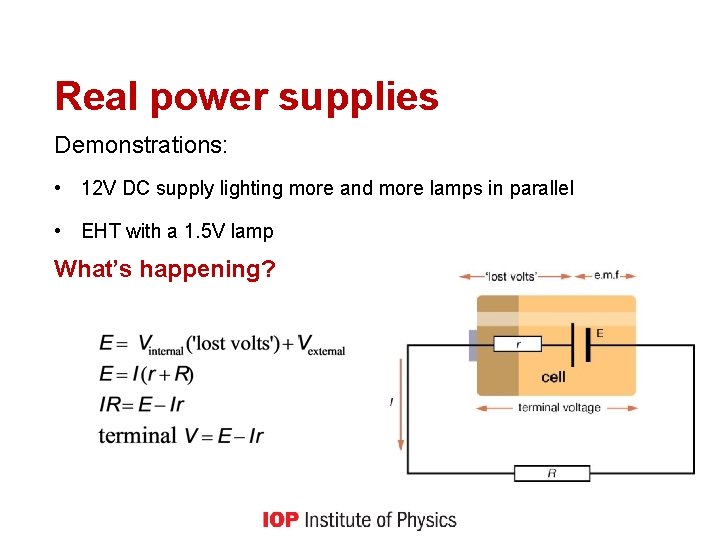
Real power supplies Demonstrations: • 12 V DC supply lighting more and more lamps in parallel • EHT with a 1. 5 V lamp What’s happening?

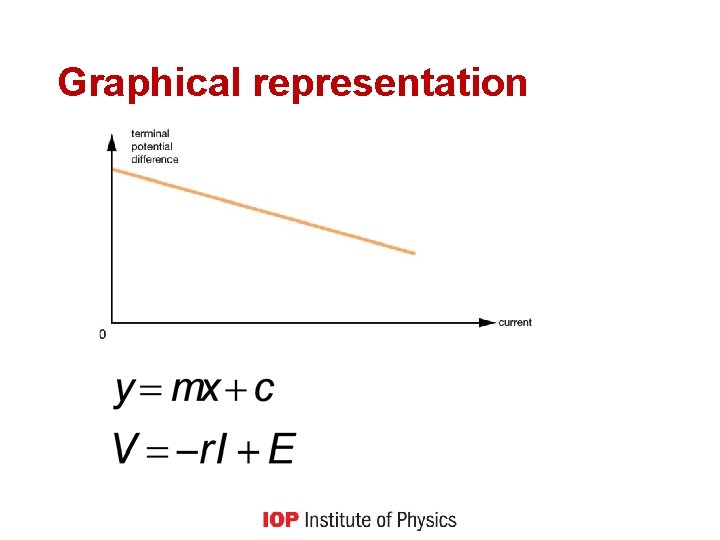
Graphical representation

Resistance in a wire microscopic picture: free electrons drifting through a metal (polycrystalline, each crystal having an ionic lattice) • constant of proportionality is resistivity, unit m • a material property Compare with rules for R networks. VPL simulation.

Current and charge Current is rate of flow of charge e. g. 1016 electrons pass a point every second Demonstration: Conduction by ‘coloured’ ions

Drift velocity where • n is the number of free electrons per unit volume • A is the cross sectional area • Δx is a small length along the wire • e is the charge of an electron

Comparing copper with tungsten metal electrons electron drift velocity in per m 3 mm s-1 copper 8. 5 × 1028 ~0. 02 tungsten 3. 4 × 1028 ~250 The difference in drift velocities explains why incandescent lamps glow white hot while their connecting wires stay safely at room temperature.

Conductivity Metal wires conduct extremely well. Conductance G = I / V , unit siemens (symbol S) • depends on the number of carriers available • ratio I / V is 'effect per unit of cause‘ Note: • conductance is the reciprocal of resistance • conductivity, [unit S m-1] is the reciprocal of resistivity

Capacitance • a measure of how much charge a capacitor can separate at a given p. d. • unit of capacitance: farad (symbol F) demonstration super-capacitor Note: There are rules for adding capacitors in networks.

Lab practicals • internal resistance of a potato cell • resistivity of a wire (using micrometer) • charging and discharging a capacitor

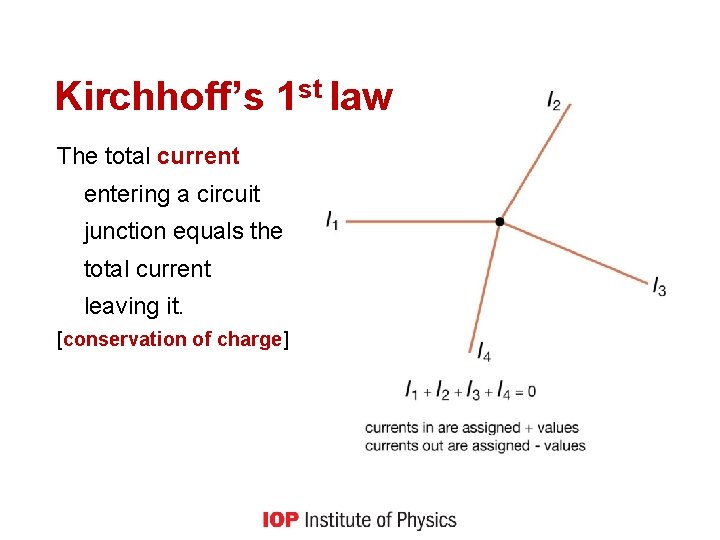
Kirchhoff’s 1 st law The total current entering a circuit junction equals the total current leaving it. [conservation of charge]

Kirchhoff’s 2 nd law The sum of the emfs round a loop in any circuit = the sum of the p. d. s round the loop. [conservation of energy] E 1 + E 2 + E 3 + … = I 1 R 1 + I 2 R 2 + I 3 R 3 + … where I 1, I 2, I 3 … represent currents through the resistances R 1, R 2, R 3 … Physlets (simulations): ‘Second semester’< ‘DC Circuits’ • ‘Kirchhoff's Loop Rule’ • ‘Applying Kirchhoff's Rules’

Kirchhoff’s 2 nd law - example A circuit consists of a cell of emf 1. 6 V in series with a resistance 2. 0 connected to a resistor of resistance 3. 0 in parallel with a resistor of resistance 6. 0 . Determine the total current drawn from the cell and the potential difference across the 3. 0 resistor.

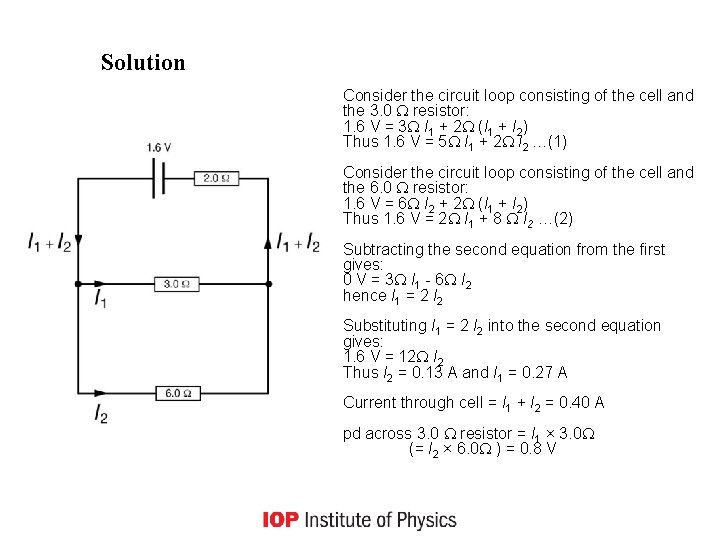
Solution Consider the circuit loop consisting of the cell and the 3. 0 resistor: 1. 6 V = 3 I 1 + 2 (I 1 + I 2) Thus 1. 6 V = 5 I 1 + 2 I 2 …(1) Consider the circuit loop consisting of the cell and the 6. 0 resistor: 1. 6 V = 6 I 2 + 2 (I 1 + I 2) Thus 1. 6 V = 2 I 1 + 8 I 2 …(2) Subtracting the second equation from the first gives: 0 V = 3 I 1 - 6 I 2 hence I 1 = 2 I 2 Substituting I 1 = 2 I 2 into the second equation gives: 1. 6 V = 12 I 2 Thus I 2 = 0. 13 A and I 1 = 0. 27 A Current through cell = I 1 + I 2 = 0. 40 A pd across 3. 0 resistor = I 1 × 3. 0 (= I 2 × 6. 0 ) = 0. 8 V

Endpoints Related topics • • • sensors of many types use the potential divider principle factors affecting capacitance (plate spacing & area, dielectric material) exponential nature of charging and discharging capacitors how ammeters and voltmeters affect circuit behaviour maximum power theorem AC circuit theory