Day 2 UNIT 1 Motion Graphs x t

Day 2 UNIT 1 Motion Graphs x t Lyzinski Physics

Day #2 * Position * Displacement * Average Velocity * Vectors * x-t graphs

Definition Position (x) – the location of an object with respect to a specified reference point. *We choose this reference point to be the origin of a coordinate system. A km -3 -2 -1 0 1 6 7 8 9 10 The position of particle “A” is either x = -3 or x = 6, depending on which reference point (or origin) you use.

Definition Displacement (Dx) – the change in an object’s position during a time interval. Dx = x 2 – x 1 or Dx = xf – xi These are all VECTORS. What’s a vector? *Displacement must have both a magnitude (size) and a direction (right, left, up, down, north, south, etc).

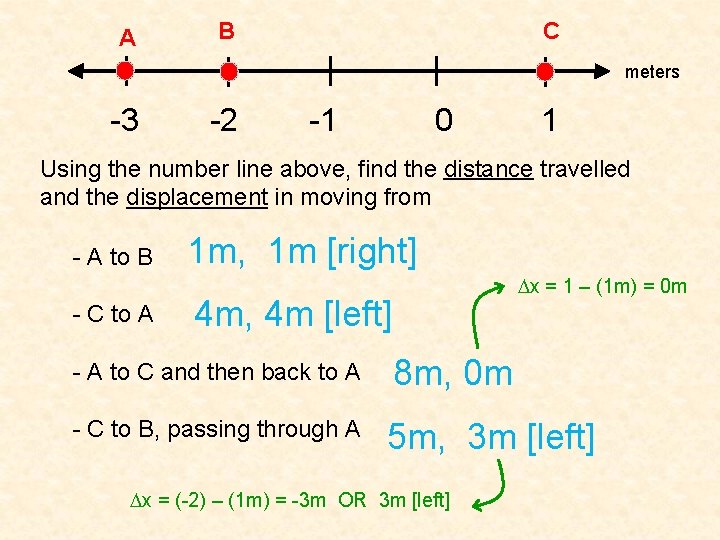
A B C meters -3 -2 -1 0 1 Using the number line above, find the distance travelled and the displacement in moving from - A to B - C to A 1 m, 1 m [right] Dx = 1 – (1 m) = 0 m 4 m, 4 m [left] - A to C and then back to A 8 m, 0 m - C to B, passing through A 5 m, 3 m [left] Dx = (-2) – (1 m) = -3 m OR 3 m [left]

Definition Average Velocity ( v ) – the displacement of an object divided by the elapsed time. v = Dx/Dt (or v=Dx/t)

Definition Vector – a quantity that has both magnitude AND a direction … oh yeh! * YES, vectors can have units. ** What vectors have we learned about thus far? position ______ displacement ______ velocity ________

Scalars vs. Vectors Displacement: has magnitude & direction Distance: has a magnitude only (example: 1 (example: 15 cm east) 6 ft) 2 B A Displacement is NEVER greater than distance traveled!

Scalars vs. Vectors (continued) Velocity: has magnitude & direction Speed: has a magnitude only (example: 15 mi/h North) 30 km/h) 2 Total time for the trip from 1 to 2: 2 hr 25 km 7 km 16 o 1 24 km Speed = d/t = 15. 5 km/h Velocity = Dx/t = 12. 5 km/h If an object STARTS & STOPS at the same point, the velocity is ZERO! (since the displacement is zero)

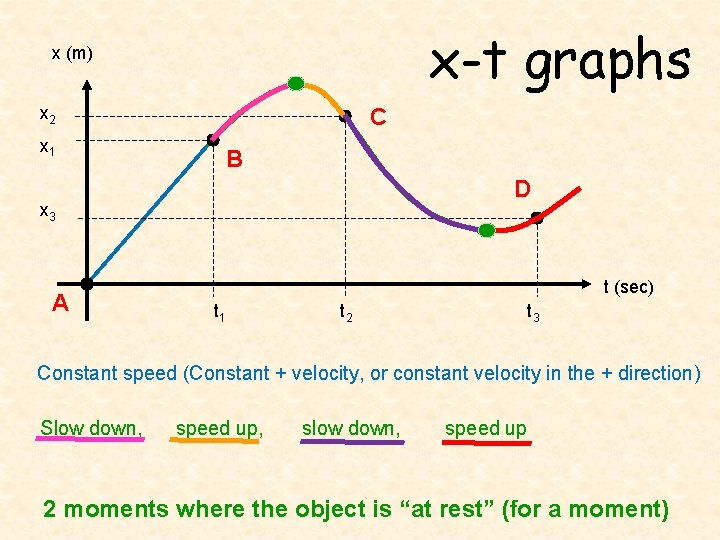
x-t graphs x (m) x 2 C x 1 B D x 3 A t (sec) t 1 t 2 t 3 Constant speed (Constant + velocity, or constant velocity in the + direction) Slow down, speed up, slow down, speed up 2 moments where the object is “at rest” (for a moment)

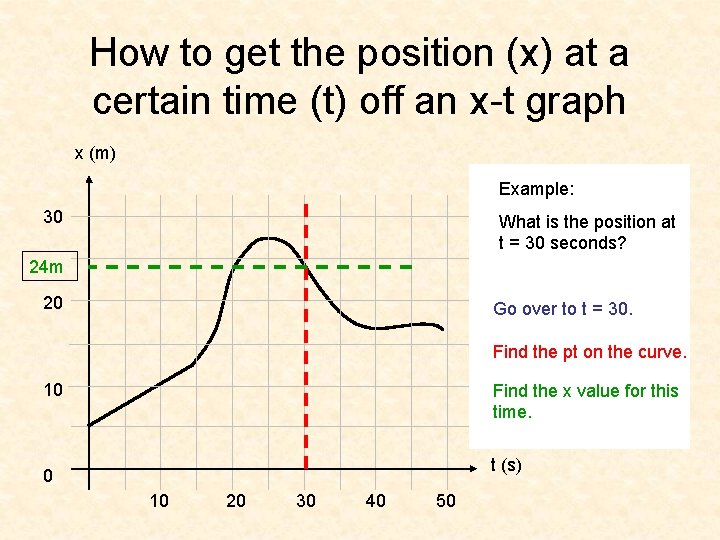
How to get the position (x) at a certain time (t) off an x-t graph x (m) Example: 30 What is the position at t = 30 seconds? 24 m 20 Go over to t = 30. Find the pt on the curve. 10 Find the x value for this time. t (s) 0 10 20 30 40 50

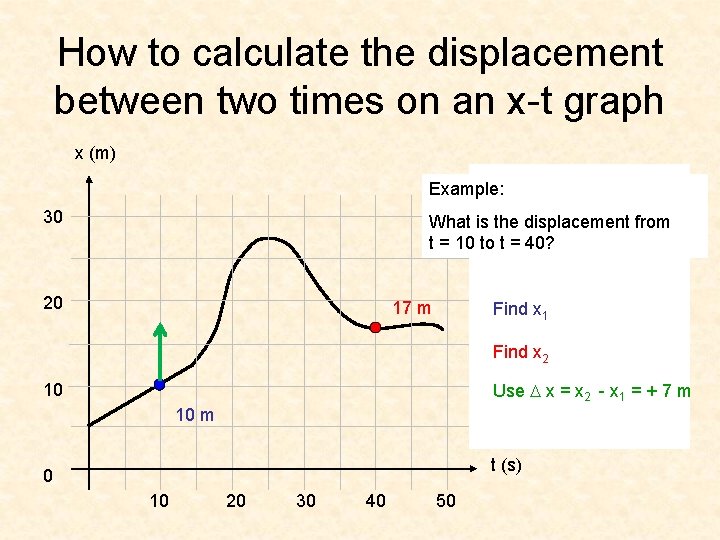
How to calculate the displacement between two times on an x-t graph x (m) Example: 30 What is the displacement from t = 10 to t = 40? 20 17 m Find x 1 Find x 2 Use D x = x 2 - x 1 = + 7 m 10 10 m t (s) 0 10 20 30 40 50

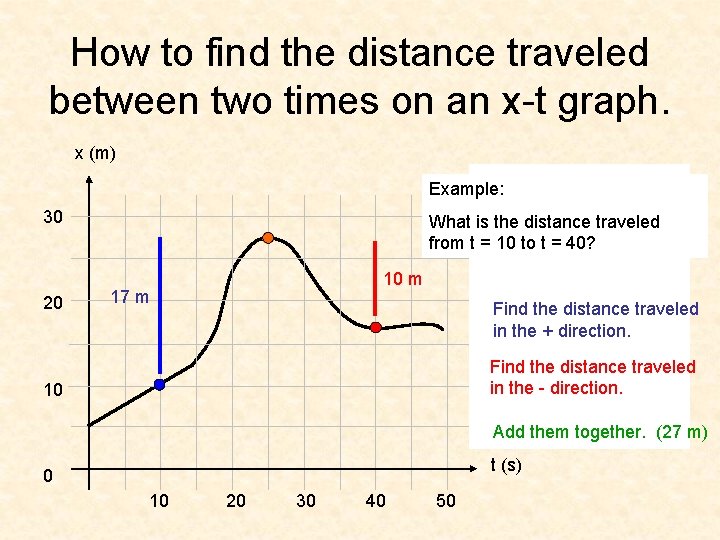
How to find the distance traveled between two times on an x-t graph. x (m) Example: 30 20 What is the distance traveled from t = 10 to t = 40? 10 m 17 m Find the distance traveled in the + direction. Find the distance traveled in the - direction. 10 Add them together. (27 m) t (s) 0 10 20 30 40 50

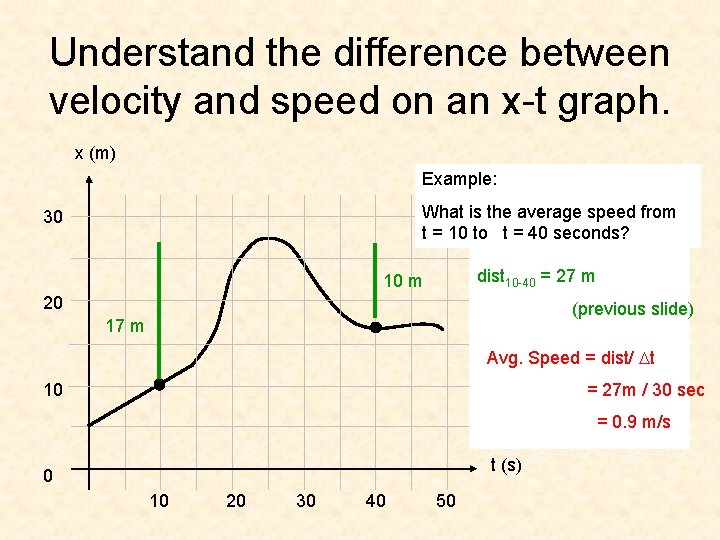
Understand the difference between velocity and speed on an x-t graph. x (m) Example: What is the average speed from t = 10 to t = 40 seconds? 30 dist 10 -40 = 27 m 10 m 20 (previous slide) 17 m Avg. Speed = dist/ Dt 10 = 27 m / 30 sec = 0. 9 m/s t (s) 0 10 20 30 40 50

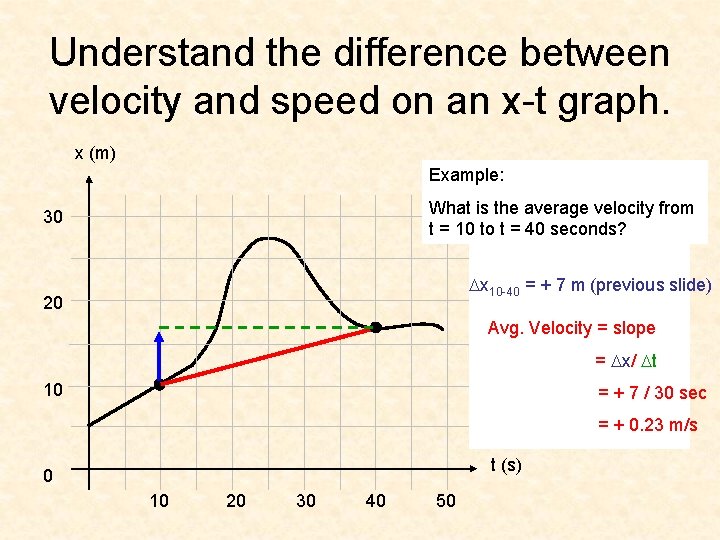
Understand the difference between velocity and speed on an x-t graph. x (m) Example: What is the average velocity from t = 10 to t = 40 seconds? 30 Dx 10 -40 = + 7 m (previous slide) 20 Avg. Velocity = slope = Dx/ Dt 10 = + 7 / 30 sec = + 0. 23 m/s t (s) 0 10 20 30 40 50

Will avg. velocity EVER be greater than avg. speed? NO!!! Will avg. velocity EVER be equal to avg. speed? YES!!! When the path travelled was one-way, in a straight line.

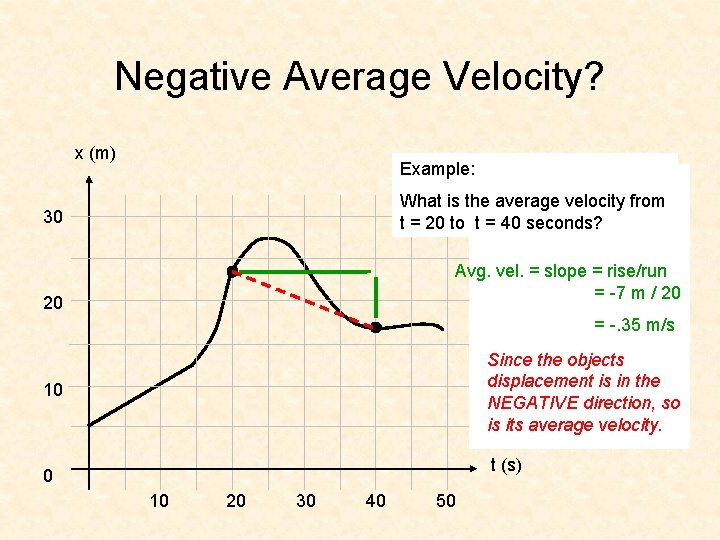
Negative Average Velocity? x (m) Example: What is the average velocity from t = 20 to t = 40 seconds? 30 Avg. vel. = slope = rise/run = -7 m / 20 20 = -. 35 m/s Since the objects displacement is in the NEGATIVE direction, so is its average velocity. 10 t (s) 0 10 20 30 40 50

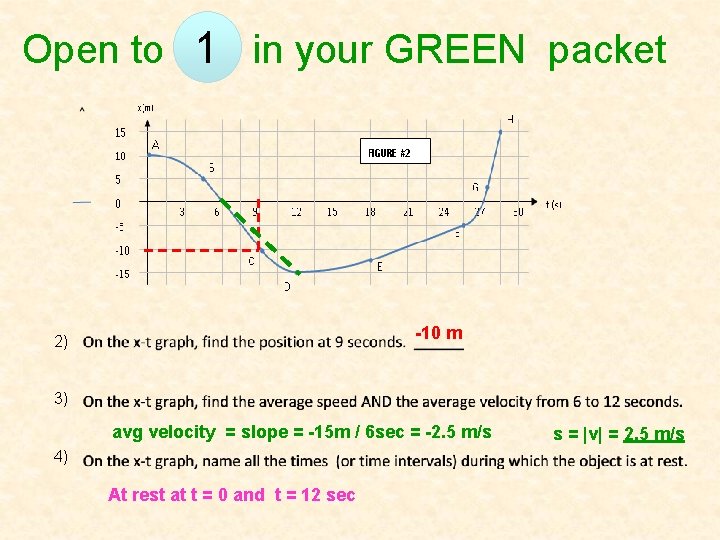
Open to 1 in your GREEN packet -10 m 2) 3) avg velocity = slope = -15 m / 6 sec = -2. 5 m/s 4) At rest at t = 0 and t = 12 sec s = |v| = 2. 5 m/s

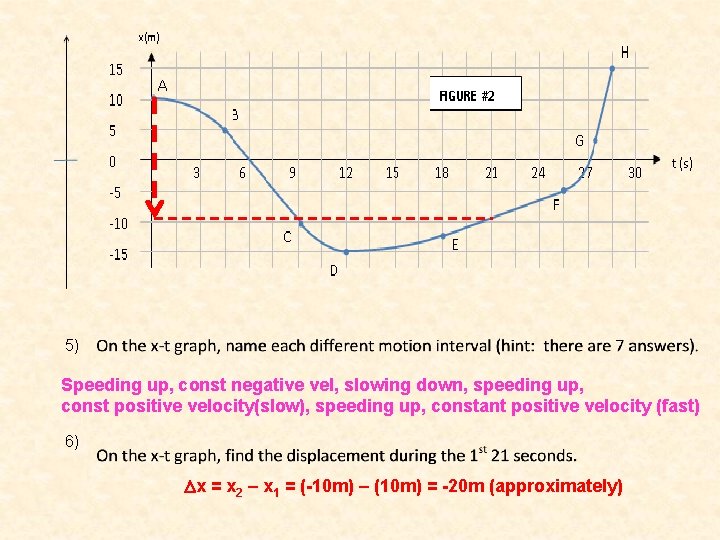
5) Speeding up, const negative vel, slowing down, speeding up, const positive velocity(slow), speeding up, constant positive velocity (fast) 6) Dx = x 2 – x 1 = (-10 m) – (10 m) = -20 m (approximately)

HOMEWORK Check out your Unit 1 Schedule … Day #2 Again, we will “try” to follow it night by night.