DAY 104 WORD PROBLEM INVOLVING SINE AND COSINE

DAY 104 – WORD PROBLEM INVOLVING SINE AND COSINE RULES

INTRODUCTION In day to day life, we encounter quite a lot of problems involving solutions of a triangle. For instance, we might know three cities or ports in different locations. We may know their bearing and the distance from one port to the other, but we may not know the distance between the other towns. In such situations, we use the sine or the cosine rule to help us solve the problem. In this lesson, we are going to understand apply the law of Sine and the law of Cosines to find unknown measurements in right and non-right triangles (e. g. , surveying problems, resultant forces).

VOCABULARY

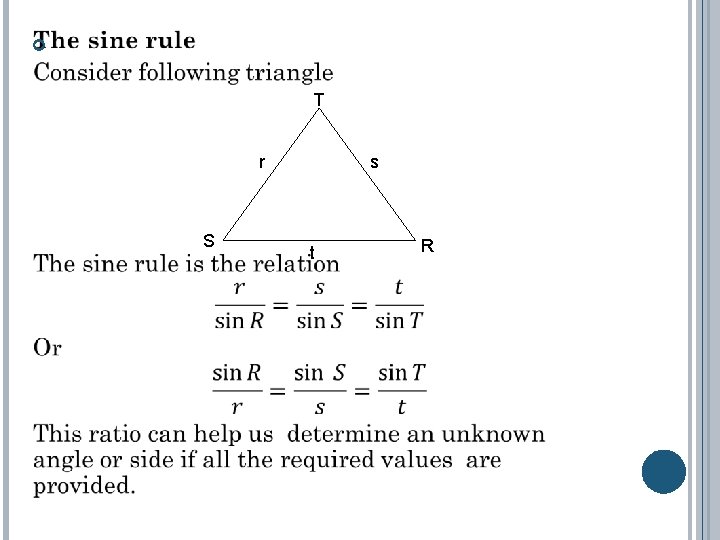
T r S s t R

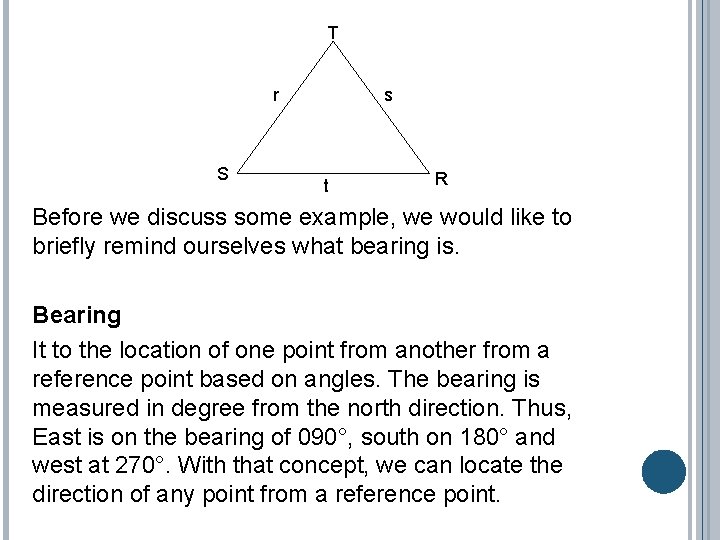
T r S s t R Before we discuss some example, we would like to briefly remind ourselves what bearing is. Bearing It to the location of one point from another from a reference point based on angles. The bearing is measured in degree from the north direction. Thus, East is on the bearing of 090°, south on 180° and west at 270°. With that concept, we can locate the direction of any point from a reference point.

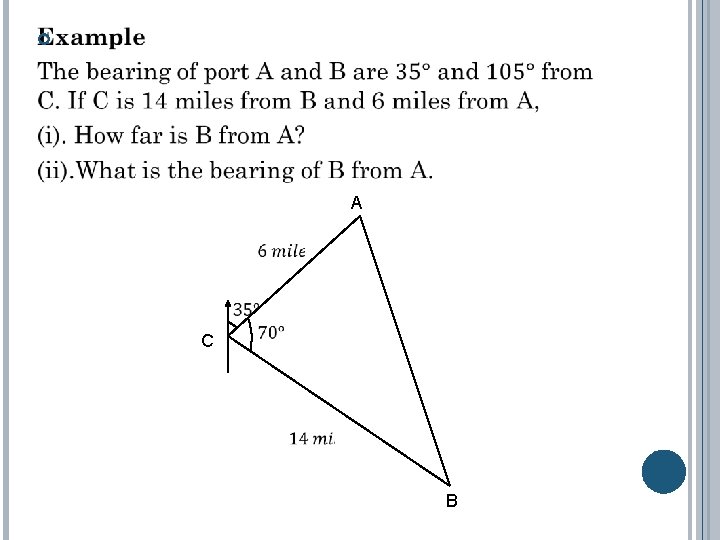
A C B

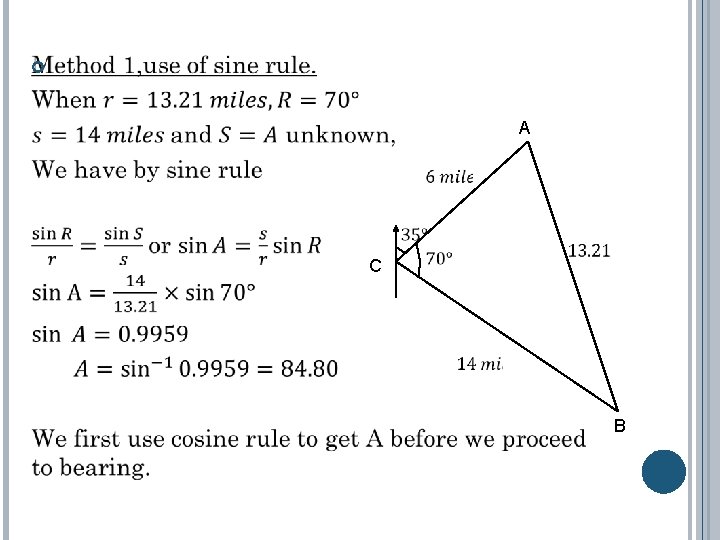
A C B

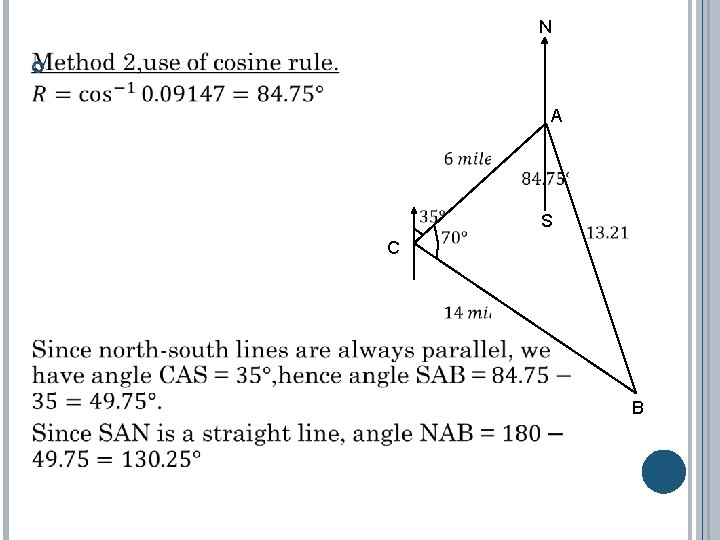
N A C S B

HOMEWORK Three water vessels, P, Q, and T are such that T is 1 mile of Q and 2. 5 miles from P. The angle between line PQ and QT is 53° and that between lines PT and TQ is 66°. How far is P from Q?

ANSWERS TO HOMEWORK

THE END