Datorntverk A lektion 7 Forts Kapitel 9 SDH

Datornätverk A – lektion 7 Forts. Kapitel 9: SDH och SONET. Kapitel 10: Felhantering.

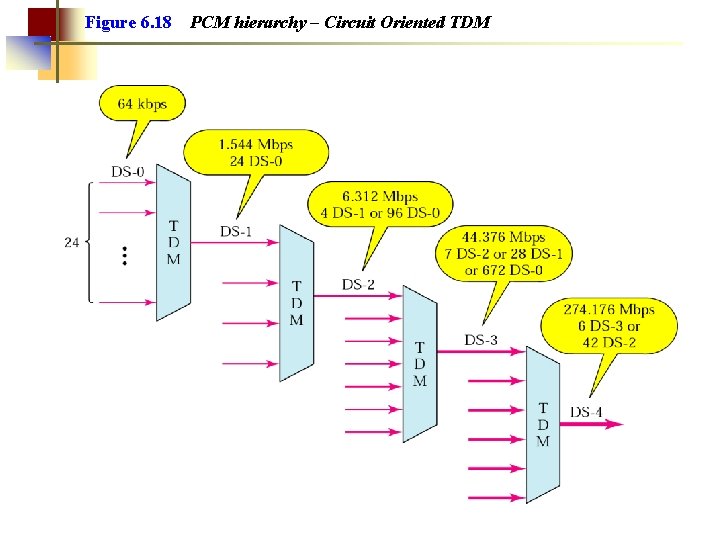
Figure 6. 18 PCM hierarchy – Circuit Oriented TDM

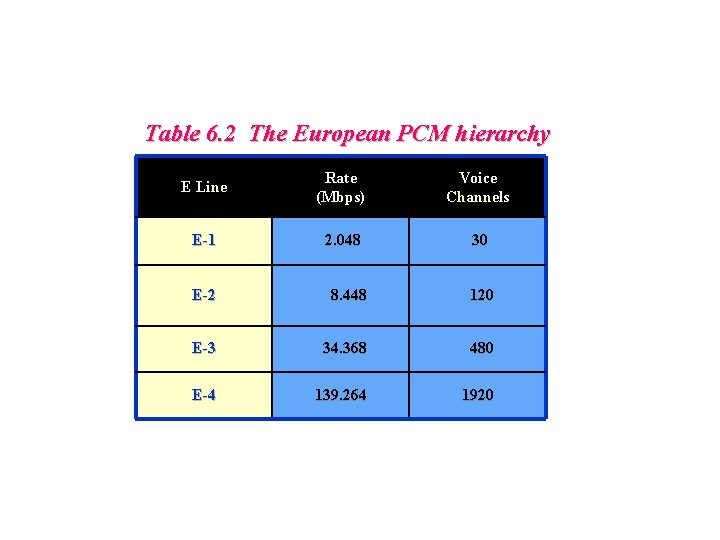
Table 6. 2 The European PCM hierarchy E Line Rate (Mbps) Voice Channels E-1 2. 048 30 E-2 8. 448 120 E-3 34. 368 480 E-4 139. 264 1920

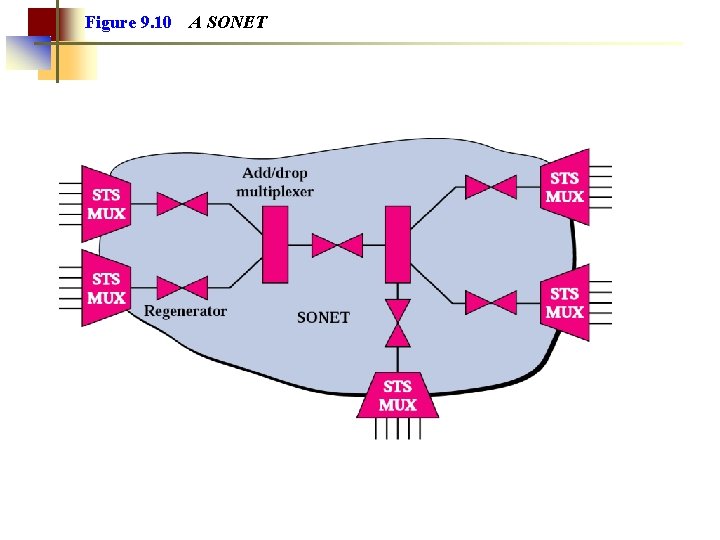
Optical Hierarchies • The old PCM hierarchy was non-synchronous ○ Different multiplexors may have slightly different clock frequency. ○ The whole hierarchy had to be unpacked in view to access or monitor a single telephone call, which was expensive. • SDH and SONET use synchronous communication ○ Clocked by a central master clock. • SDH (Synchronous Digital Hierarchy) ○ A standard for TDM in Europe • SONET (Synchronious Optical NETwork) ○ A standard for TDM used in United States • IP-over-SDH/SONET allows several ISP: s to share the same fiber cable independently.

Note: SONET and SDH are synchronous TDM systems controlled by a master clock.

Figure 9. 10 A SONET

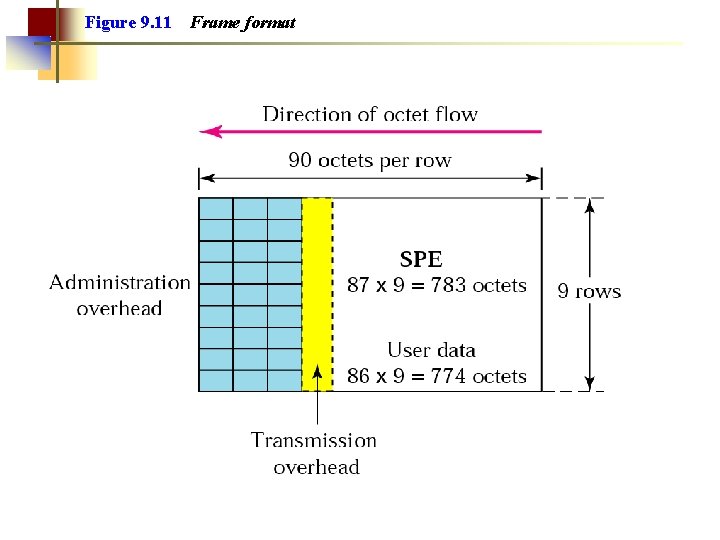
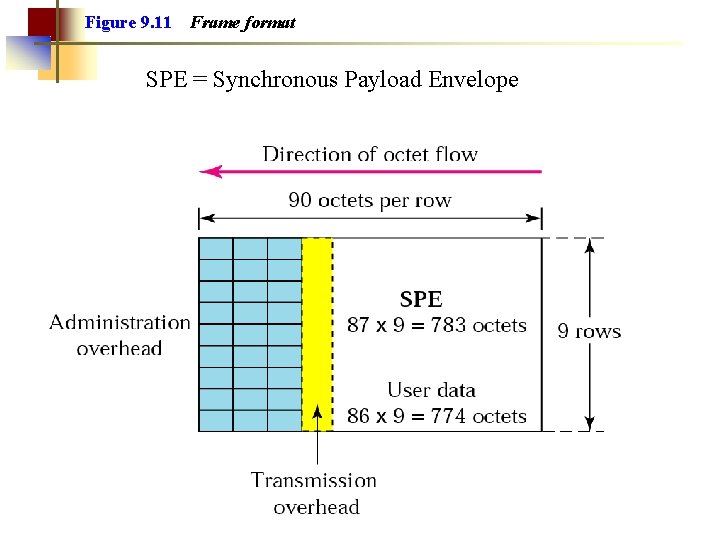
Figure 9. 11 Frame format

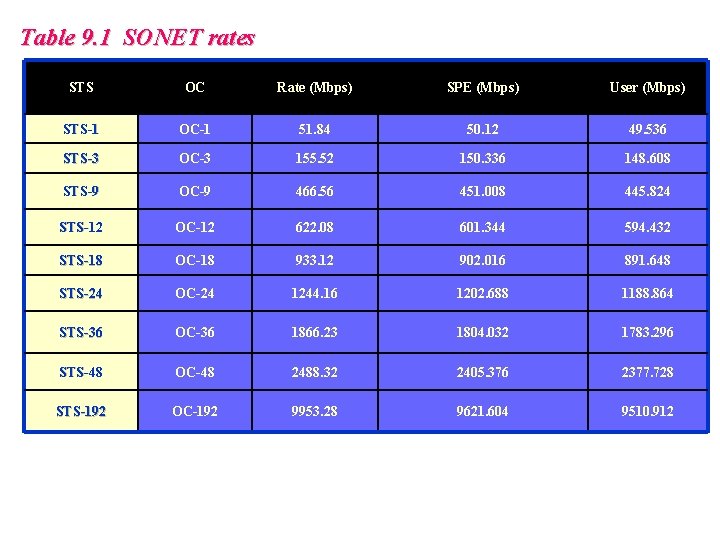
Table 9. 1 SONET rates STS OC Rate (Mbps) SPE (Mbps) User (Mbps) STS-1 OC-1 51. 84 50. 12 49. 536 STS-3 OC-3 155. 52 150. 336 148. 608 STS-9 OC-9 466. 56 451. 008 445. 824 STS-12 OC-12 622. 08 601. 344 594. 432 STS-18 OC-18 933. 12 902. 016 891. 648 STS-24 OC-24 1244. 16 1202. 688 1188. 864 STS-36 OC-36 1866. 23 1804. 032 1783. 296 STS-48 OC-48 2488. 32 2405. 376 2377. 728 STS-192 OC-192 9953. 28 9621. 604 9510. 912

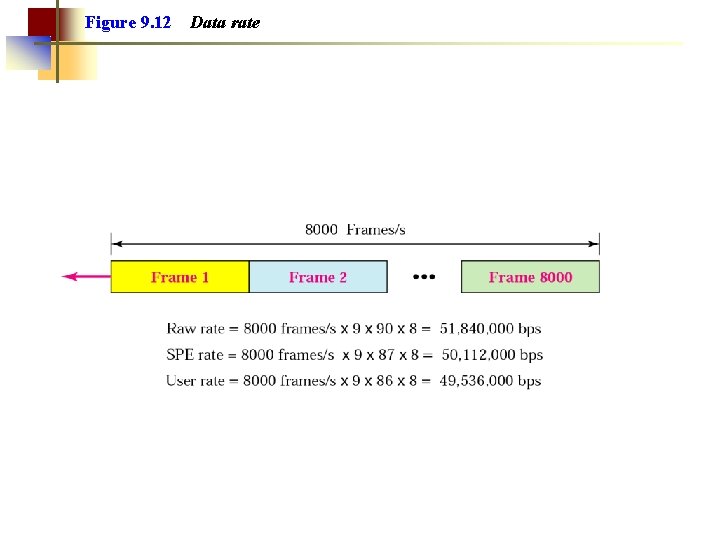
Figure 9. 12 Data rate

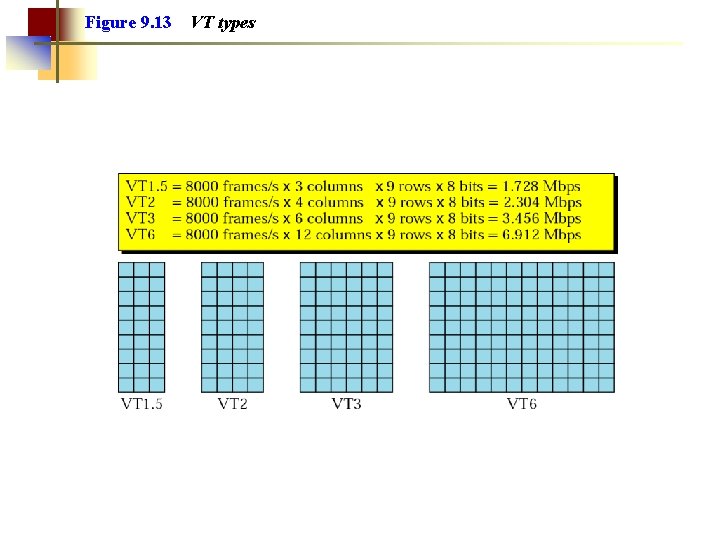
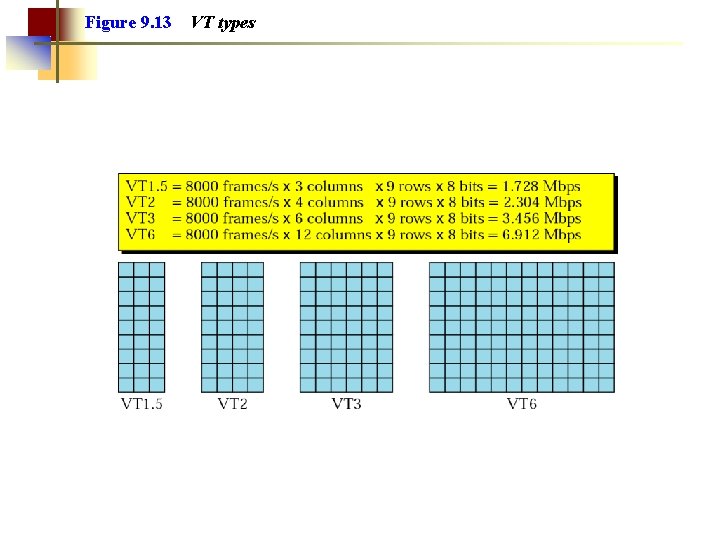
Figure 9. 13 VT types

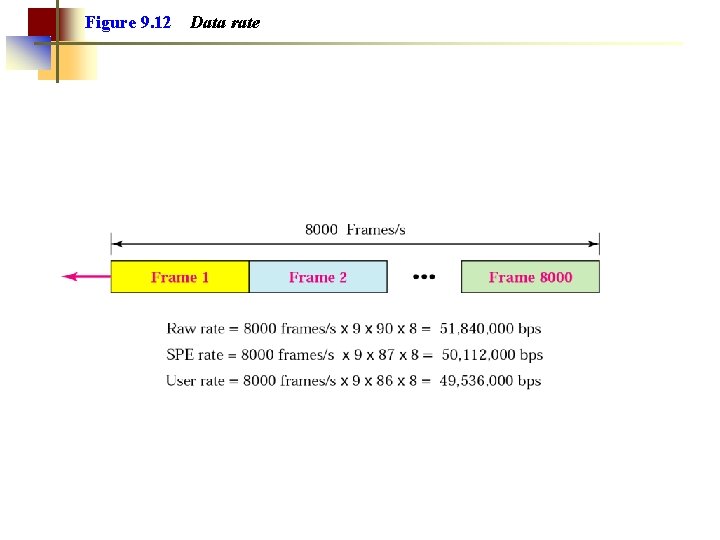
Figure 9. 12 Data rate

Figure 9. 11 Frame format SPE = Synchronous Payload Envelope

Figure 9. 13 VT types

PART III Data Link Layer

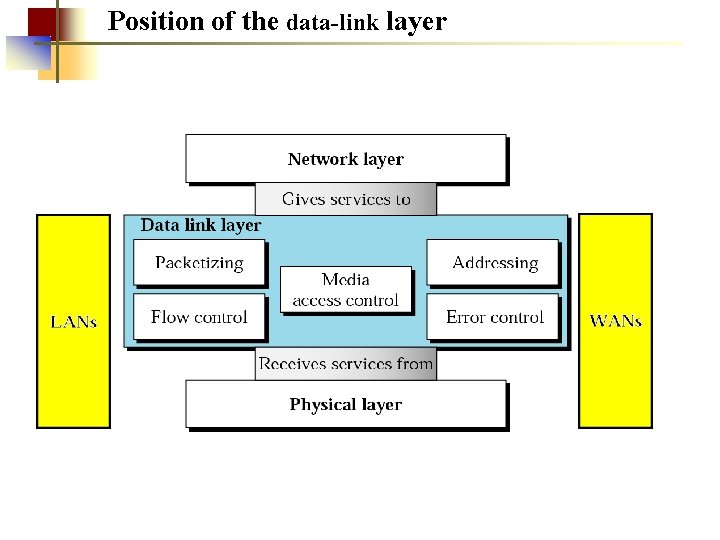
Position of the data-link layer

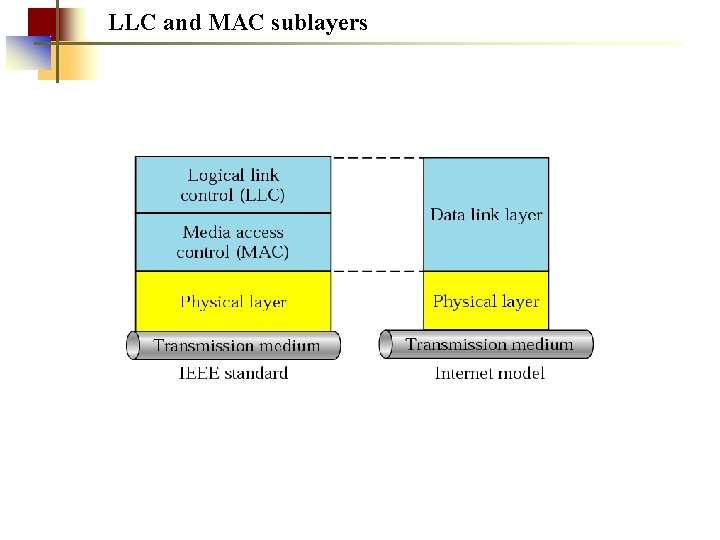
LLC and MAC sublayers

IEEE standards for LANs

Chapter 10 Error Detection and Correction

Note: Data can be corrupted during transmission. For reliable communication, errors must be detected and corrected.

10. 1 Types of Error Single-Bit Error Burst Error

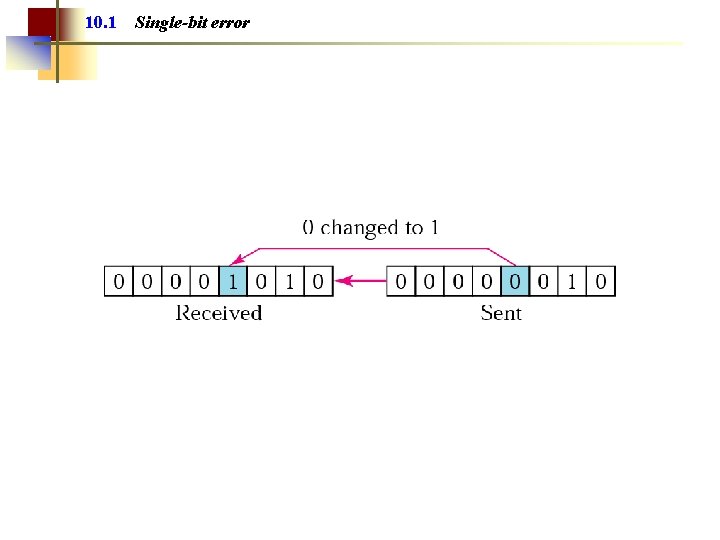
Note: In a single-bit error, only one bit in the data unit has changed.

10. 1 Single-bit error

Note: A burst error means that 2 or more bits in the data unit have changed.

10. 2 Burst error of length 5

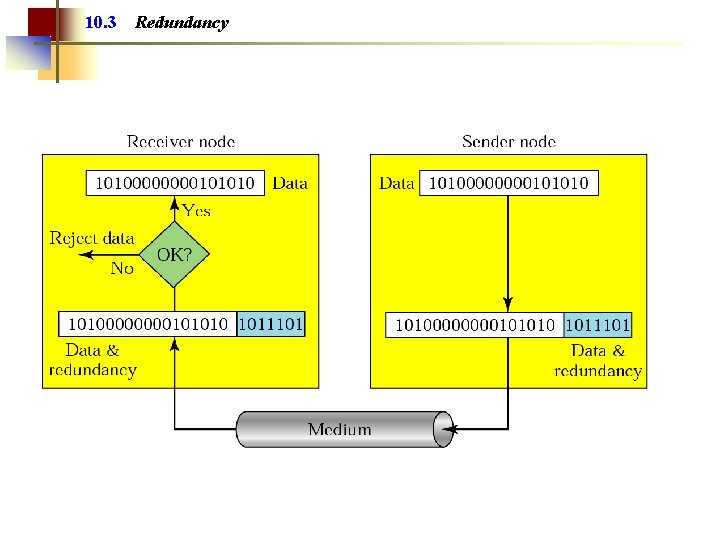
Note: Error detection uses the concept of redundancy, which means adding extra bits for detecting errors at the destination.

10. 3 Redundancy

10. 4 Detection methods

Note: In parity check, a parity bit is added to every data unit so that the total number of 1 s is even (or odd for odd-parity).

Example 1 Suppose the sender wants to send the word world. In ASCII (7 -bit code) the five characters are coded as 11101111 1110010 1101100100 Even parity is used. The following shows the actual bits sent: 1110 110111100100 11011000 11001001

Example 3 Now suppose the word world in Example 1 is received by the receiver without being corrupted in transmission. 1110 110111100100 11011000 11001001 The receiver counts the 1 s in each character and comes up with even numbers (6, 6, 4, 4, 4). The data are accepted. Now suppose the word world in Example 1 is corrupted during transmission. 11111110 110111101100 11011000 11001001 The receiver counts the 1 s in each character and comes up with even and odd numbers (7, 6, 5, 4, 4). The receiver knows that the data are corrupted, discards them, and asks for retransmission.

Note: Simple parity check can detect all single-bit errors. It can detect burst errors only if the total number of errors in each data unit is odd.

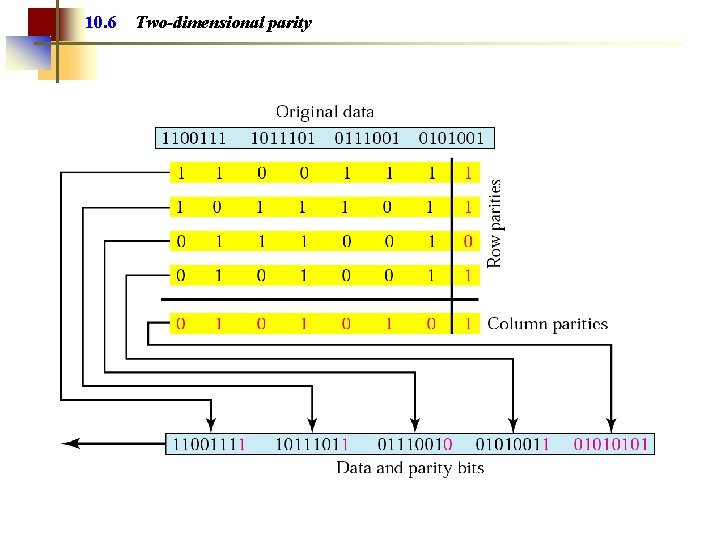
Note: In two-dimensional parity check, a block of bits is divided into rows and a redundant row of bits is added to the whole block.

10. 6 Two-dimensional parity

Example 4 Suppose the following block is sent: 10101001 00111001 1101 11100111 1010 However, it is hit by a burst noise of length 8, and some bits are corrupted. 101000001001 1101 11100111 1010 When the receiver checks the parity bits, some of the bits do not follow the even-parity rule and the whole block is discarded. 101000001001 1101 11100111 1010

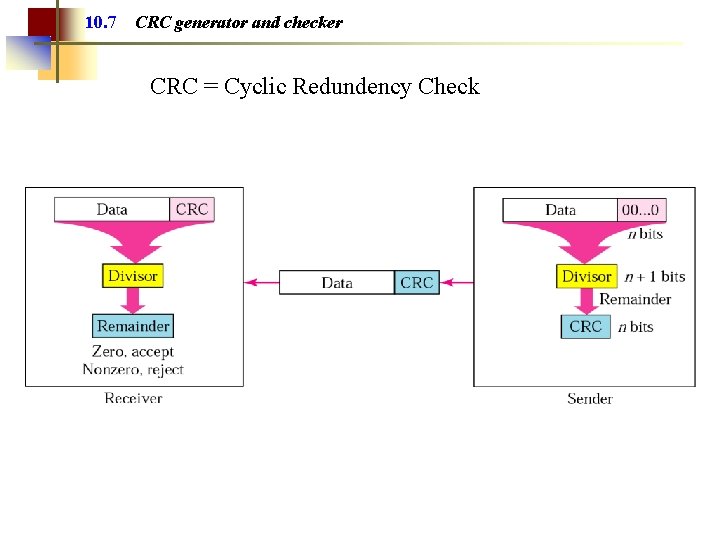
10. 7 CRC generator and checker CRC = Cyclic Redundency Check

”Vanlig” division (Kvot) 03 5 (Nämnare) 171 7 Nominator (Täljare) . 15 2 Reminder (Rest) Haltande liknelse med CRC: Om vi subtraherar täljaren (17) med resten (2) vi ett tal som är jämnt delbart med nämnaren (5). Om mottagaren tar emot något som inte är delbart med 5 har sannolikt att bitfel uppstått.

Modulo 2 Arithmetic • In modulo 2 arithmetic addition and substruction are identical to EXCLUSUVE OR (XOR) operation. • Multiplication and division are the same as in base-2 arithmetic without carries in addition or borrows in substraction. 0 XOR 0 = 0 0 XOR 1 = 1 1 XOR 0 = 1 1 XOR 1 = 0 Examples: 1011 XOR 0101 = 1110 1001 XOR 1101 = 0100

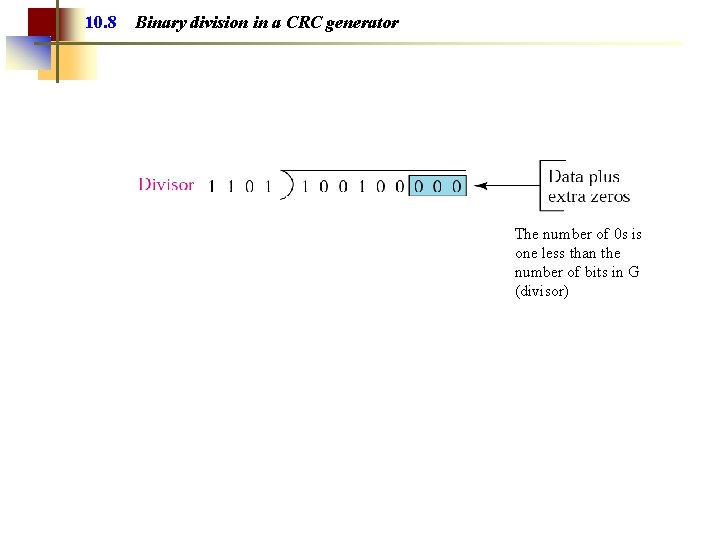
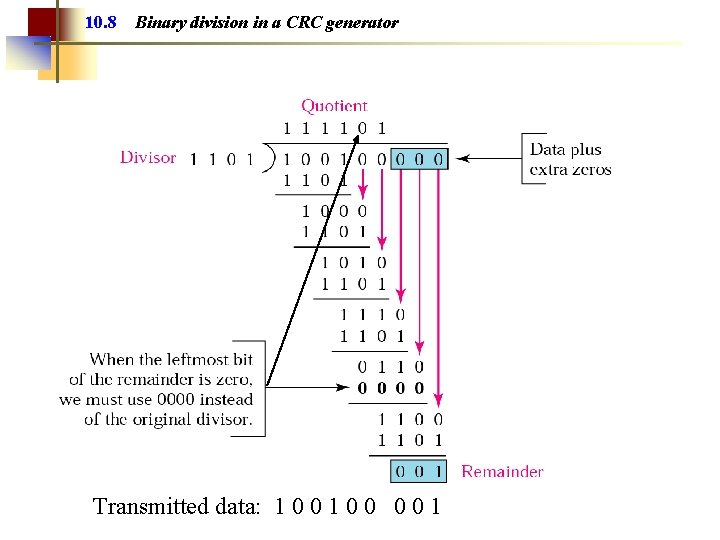
10. 8 Binary division in a CRC generator The number of 0 s is one less than the number of bits in G (divisor)

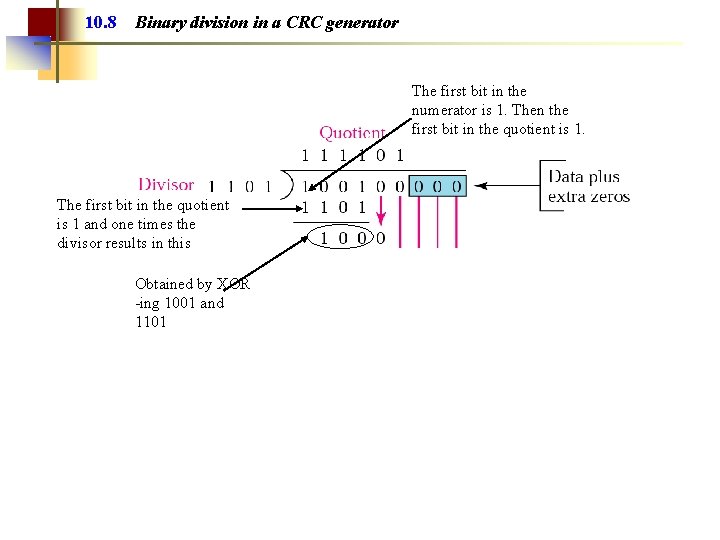
10. 8 Binary division in a CRC generator The first bit in the numerator is 1. Then the first bit in the quotient is 1. The first bit in the quotient is 1 and one times the divisor results in this Obtained by XOR -ing 1001 and 1101

10. 8 Binary division in a CRC generator Transmitted data: 1 0 0 0 0 1

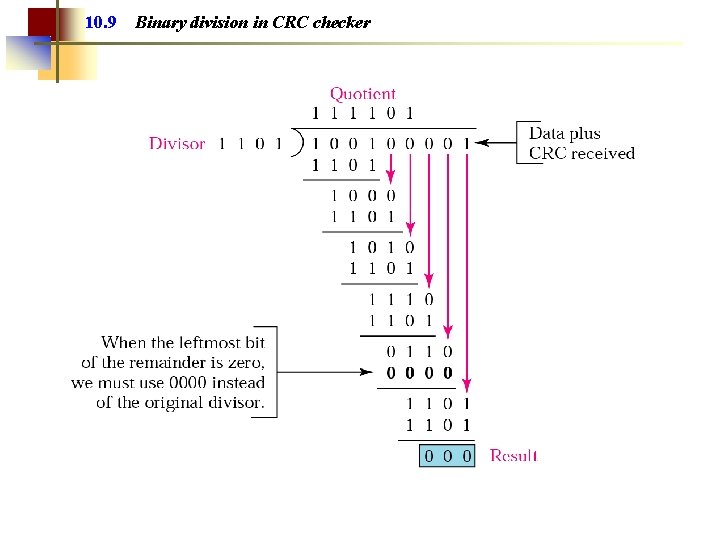
10. 9 Binary division in CRC checker

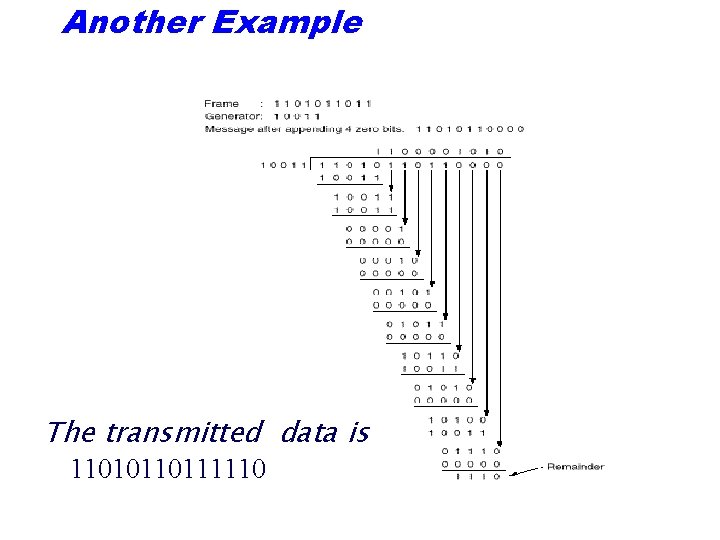
Another Example The transmitted data is 11010110111110

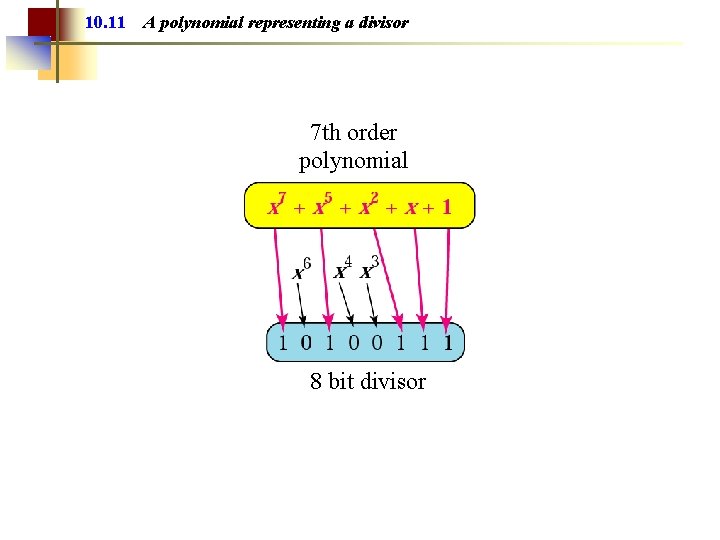
10. 11 A polynomial representing a divisor 7 th order polynomial 8 bit divisor

Polynomyal representation • Based upon discrete mathetematics, where bit strings are treated as polynomials. • k bit divisor is represented as (k-1) degree polynomial with coefficients 0 and 1. • Example: 1010110 has 7 bits • It can be represented as a polynomial of 6 th degree 1·x 6 + 0·x 5 + 1·x 4 +0·x 3 + 1·x 2 + 1·x 1 + 0·x 0 = x 6 + x 4 + x 2 + x

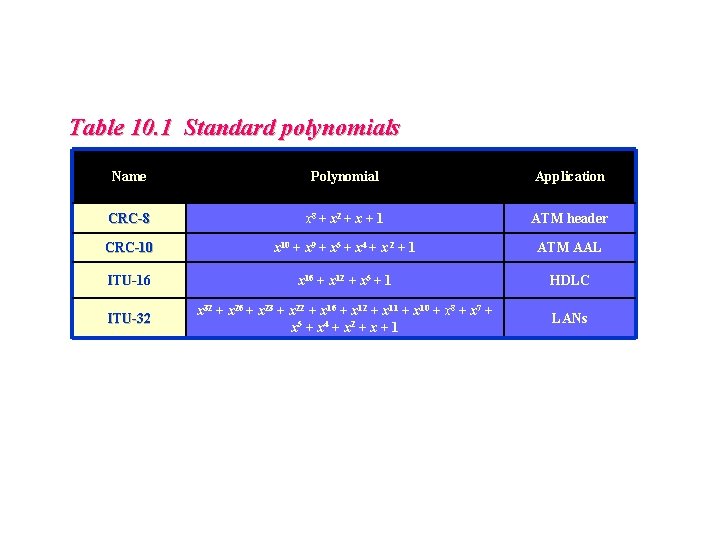
Table 10. 1 Standard polynomials Name Polynomial Application CRC-8 x 8 + x 2 + x + 1 ATM header CRC-10 x 10 + x 9 + x 5 + x 4 + x 2 + 1 ATM AAL ITU-16 x 16 + x 12 + x 5 + 1 HDLC ITU-32 x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 LANs

Example 5 It is obvious that we cannot choose x (binary 10), x 2 (binary 100), etc, because then the reminder is 0. We cannot chose a polynomial that is divisible by x, for example x 2 + x (binary 110). However, we can choose x + 1 (binary 11) because it is not divisible by x, but is divisible by x + 1. We can also choose x 2 + 1 (binary 101) because it is divisible by x + 1 (binary division).

How CRC Operates • The sender wants to send k bits message • The sender and the receiver must agree in advance on n+1 bit string called generator polynomial (divisor), G. ○ G can be represented as n-degree polynomial • n redundant bits are added to the k bits message. They are called CRC bits. k bits Data bits to be sent n bits CRC bits

How CRC Operates (Cont. ) • The redundant bits are chosen in such a way that the resulting k+n bit string is exactly divisible (with a reminder=0) by G using modulo 2 arithmetic. • The receiver divides the received data together with the CRC bits by G using modulo 2 arithmetic. ○ If the reminder is 0, then the string is considered to be without errors ○ If the reminder is not 0, the data unit is with errors and it is rejected

Example 6 The CRC-12 x 12 + x 11 + x 3 + x + 1 which has a degree of 12, will detect all burst errors affecting an odd number of bits, will detect all burst errors with a length less than or equal to 12, and will detect, 99. 97 percent of the time, burst errors with a length of 12 or more.

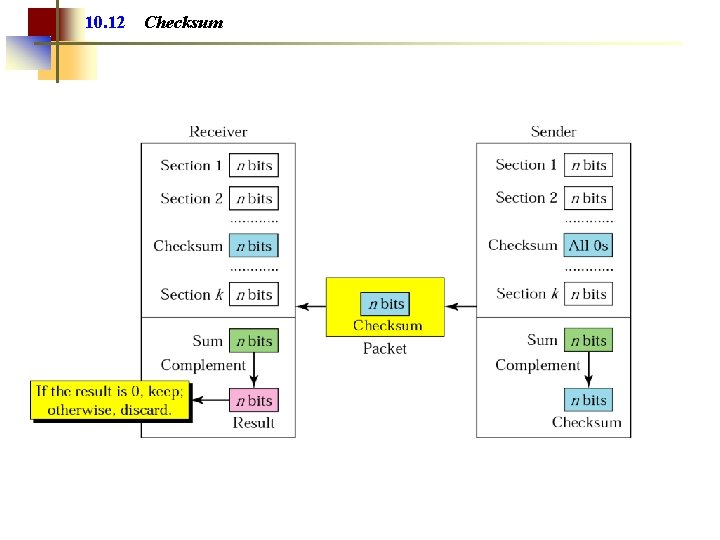
10. 12 Checksum

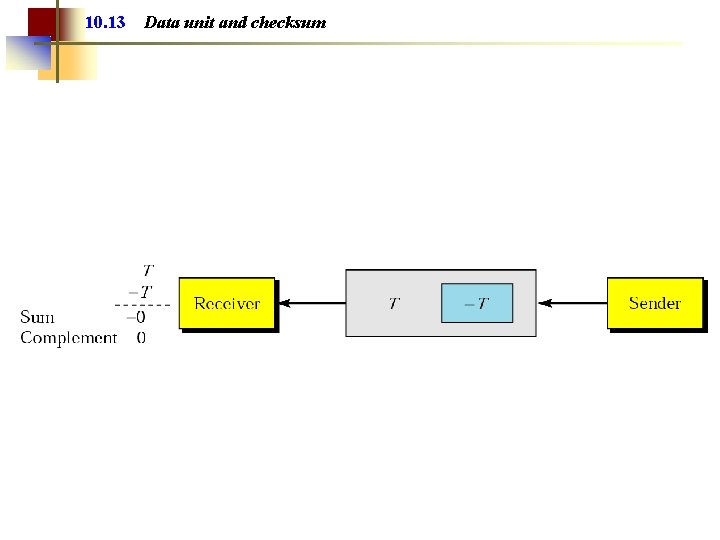
10. 13 Data unit and checksum

Note: The sender follows these steps: • The unit is divided into k sections, each of n bits. • All sections are added using one’s complement to get the sum. • The sum is complemented and becomes the checksum. • The checksum is sent with the data.

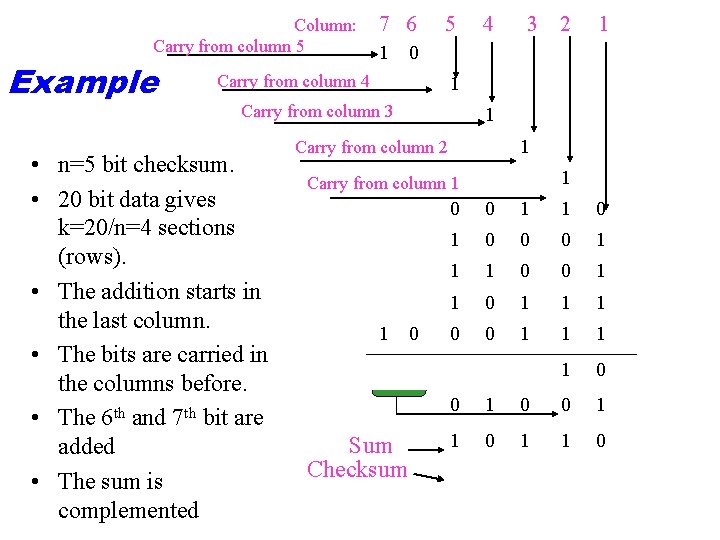
Column: Carry from column 5 Example 7 6 5 3 2 1 1 0 Carry from column 4 1 Carry from column 3 • n=5 bit checksum. • 20 bit data gives k=20/n=4 sections (rows). • The addition starts in the last column. • The bits are carried in the columns before. • The 6 th and 7 th bit are added • The sum is complemented 4 1 1 Carry from column 2 1 Carry from column 1 1 0 Sum Checksum 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 0

Example 7 Suppose the following block of 16 bits is to be sent using a checksum of 8 bits. 10101001 00111001 The numbers are added using one’s complement 10101001 Sum 00111001 ------11100010 Checksum 00011101 The pattern sent is 10101001 00111001 00011101

Example 8 Now suppose the receiver receives the pattern sent in Example 7 and there is no error. 10101001 00111001 00011101 When the receiver adds the three sections, it will get all 1 s, which, after complementing, is all 0 s and shows that there is no error. 10101001 00111001 00011101 Sum 1111 Complement 0000 means that the pattern is OK.

Note: The receiver follows these steps: • The unit is divided into k sections, each of n bits. • All sections are added using one’s complement to get the sum. • The sum is complemented. • If the result is zero, the data are accepted: otherwise, rejected.

Example 9 Now suppose there is a burst error of length 5 that affects 4 bits. 101011111001 00011101 When the receiver adds the three sections, it gets 101011111001 00011101 Partial Sum 1 11000101 Carry Sum Complement 1 11000110 00111001 the pattern is corrupted.

Felrättande koder FEC = Forward Error Correction = Felrättande koder. Två typer: 1. Faltningskoder (convolutional codes). Ex: Vid Faltningskod med kodtakt (code rate) 1/3 infogas en redundant bit mellan varje bit i nyttomeddelandet. 2. Blockkoder Ex: Vid Read Salomon-kod med beteckningen RS(128, 16), har man 128 bytes nyttodata och 16 bytes redundant felupptäckande kod i varje block.