Datorntverk A lektion 3 MKS B lektion 3

Datornätverk A – lektion 3 MKS B – lektion 3 §Kapitel 3: Fysiska signaler.
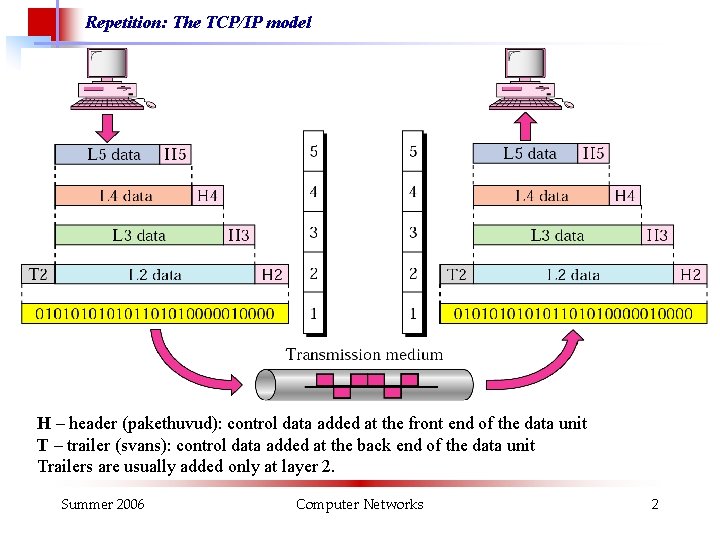
Repetition: The TCP/IP model H – header (pakethuvud): control data added at the front end of the data unit T – trailer (svans): control data added at the back end of the data unit Trailers are usually added only at layer 2. Summer 2006 Computer Networks 2

PART II Physical Layer Summer 2006 Computer Networks 3

Chapter 3 – Time and Frequency Domain Concept, Transmission Impairments
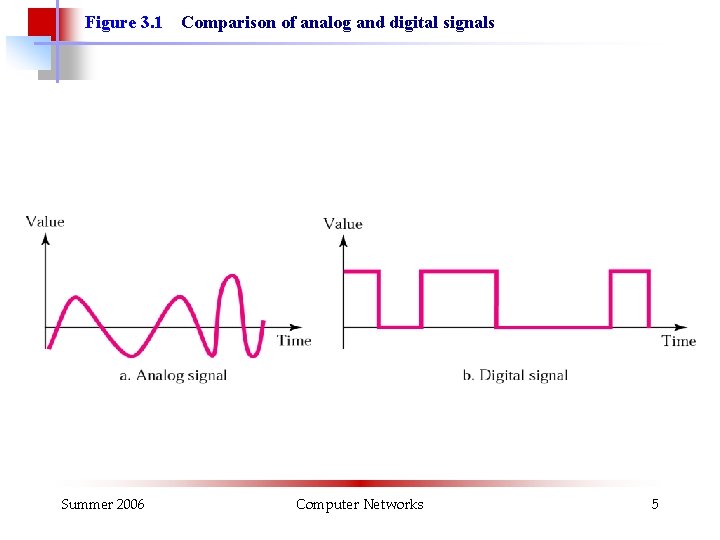
Figure 3. 1 Summer 2006 Comparison of analog and digital signals Computer Networks 5

Note: Signals can be analog or digital. Analog signals can have an infinite number of values in a range; digital signals can have only a limited number of values. Summer 2006 Computer Networks 6

Periodic vs. Non Periodic Signals § Periodic signal § repeat over and over again, once period § The period ( T ) is the time it takes to make one complete cycle § Non periodic signal § Doesn’t repeat according to any particular pattern § Direct current, noise or impulses Summer 2006 Computer Networks 7

Sinusvågor Periodtid T = t 2 - t 1. Enhet: s. Frekvens f = 1/T. Enhet: 1/s=Hz. T=1/f. Amplitud eller toppvärde Û. Enhet: Volt. Fasläge: θ = 0 i ovanstående exempel. Enhet: Grader eller radianer. Momentan spänning: u(t)= Ûsin(2πft+θ) Summer 2006 Computer Networks 8
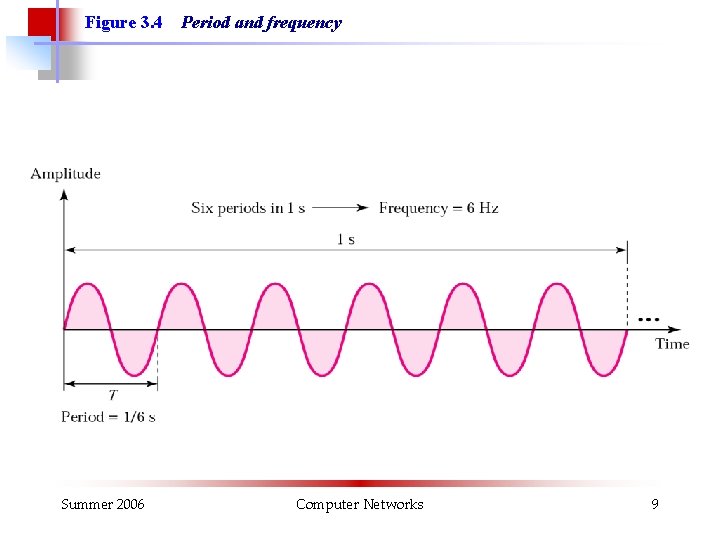
Figure 3. 4 Summer 2006 Period and frequency Computer Networks 9

Tabell 3. 1 Enheter för periodtid och frekvens Enhet Sekunder (s) Ekvivalent 1 s Enhet Hertz (Hz) Ekvivalent 1 Hz Millisekunder (ms) 10– 3 s Kilohertz (k. Hz) 103 Hz Mikrosekunder (μs) 10– 6 s Megahertz (MHz) 106 Hz Nanosekunder (ns) 10– 9 s Gigahertz (GHz) 109 Hz Pikosekunder (ps) 10– 12 s Terahertz (THz) 1012 Hz Exempel: En sinusvåg med periodtid 1 ns har frekvens 1 GHz. Summer 2006 Computer Networks 10
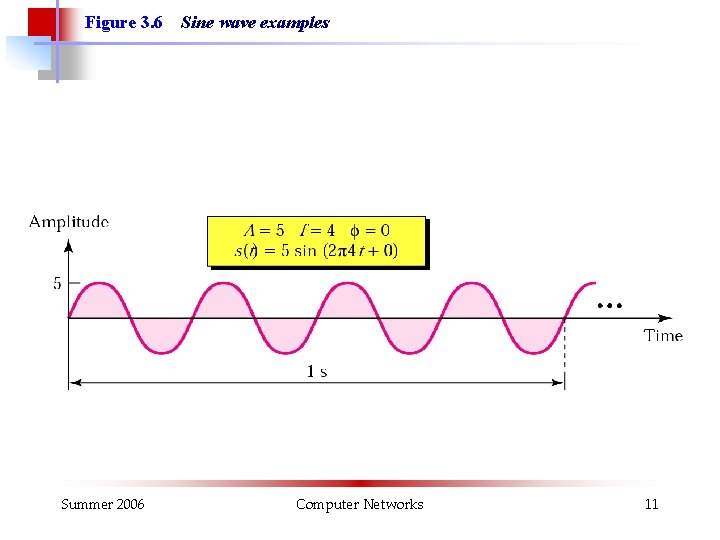
Figure 3. 6 Summer 2006 Sine wave examples Computer Networks 11
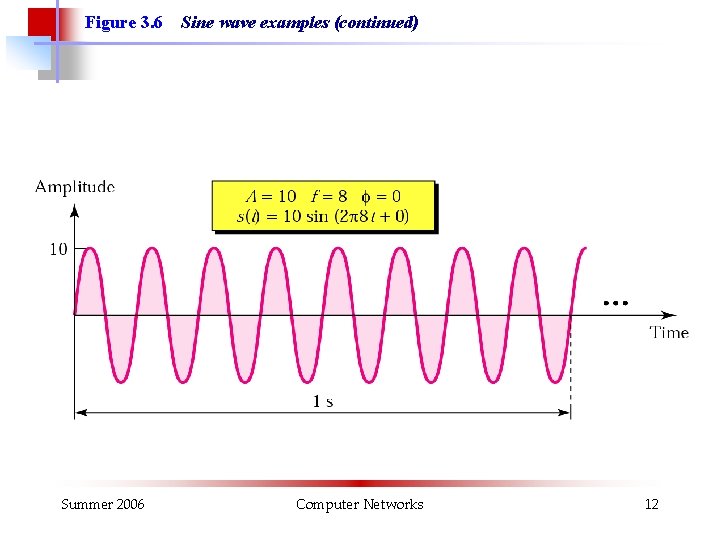
Figure 3. 6 Summer 2006 Sine wave examples (continued) Computer Networks 12

Exempel Vilken frekvens i k. Hz har en sinusvåg med periodtid 100 ms? Lösning Alternativ 1: Gör om till grundenheten. 100 ms = 0. 1 s f = 1/0. 1 Hz = 10/1000 k. Hz = 0. 01 k. Hz Alternativ 2: Utnyttja att 1 ms motsvarar 1 k. Hz. f = 1/100 ms = 0. 01 k. Hz. Summer 2006 Computer Networks 13
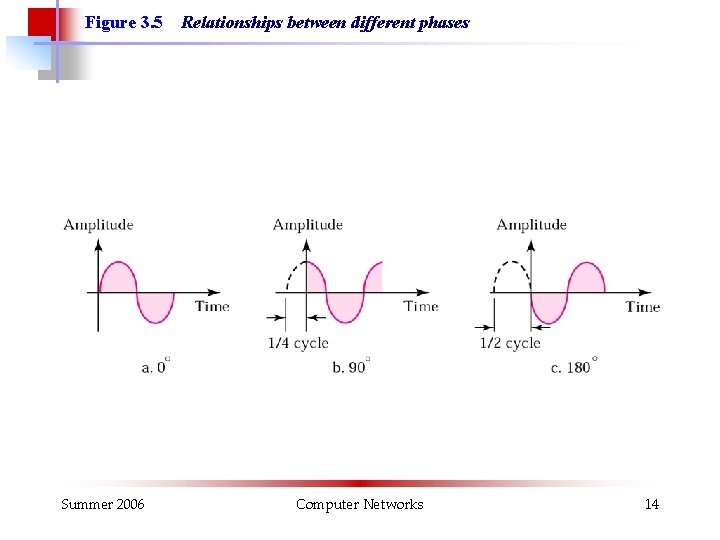
Figure 3. 5 Summer 2006 Relationships between different phases Computer Networks 14

Measuring the Phase § The phase is measured in degrees or in radians. § One full cycle is 360 o (degrees) = 2 p (radians) p 3. 14 Example: A sine wave is offset one-sixth of a cycle with respect to time 0. What is the phase in radians? Solution: (1/6) 360 = 60 degrees = 60 x 2 p /360 rad = 1. 046 rad Summer 2006 Computer Networks 15
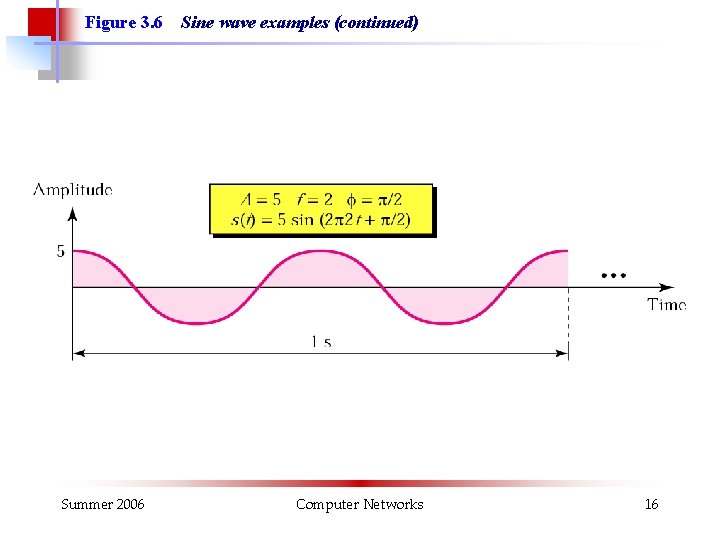
Figure 3. 6 Summer 2006 Sine wave examples (continued) Computer Networks 16

Example 2 A sine wave is offset one-sixth of a cycle with respect to time zero. What is its phase in degrees and radians? Solution We know that one complete cycle is 360 degrees. Therefore, 1/6 cycle is (1/6) 360 = 60 degrees = 60 x 2 p /360 rad = 1. 046 rad Summer 2006 Computer Networks 17
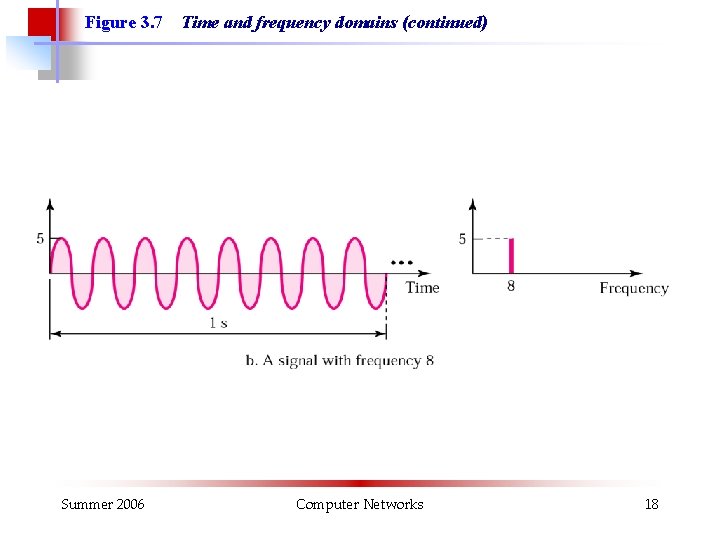
Figure 3. 7 Summer 2006 Time and frequency domains (continued) Computer Networks 18
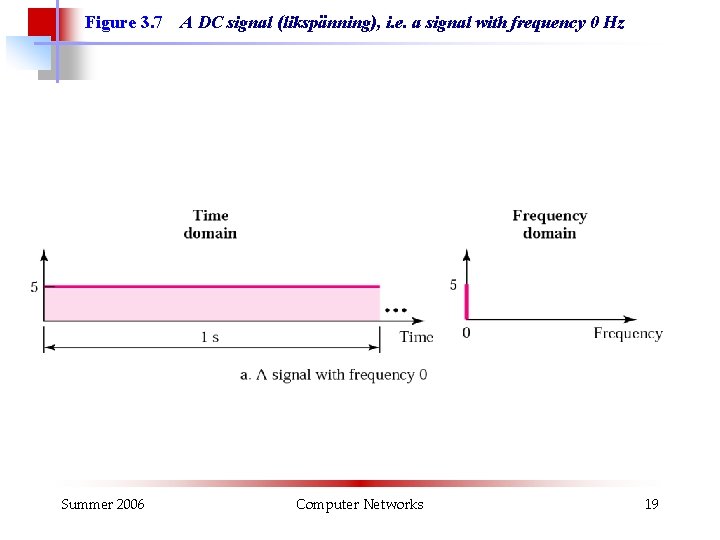
Figure 3. 7 Summer 2006 A DC signal (likspänning), i. e. a signal with frequency 0 Hz Computer Networks 19
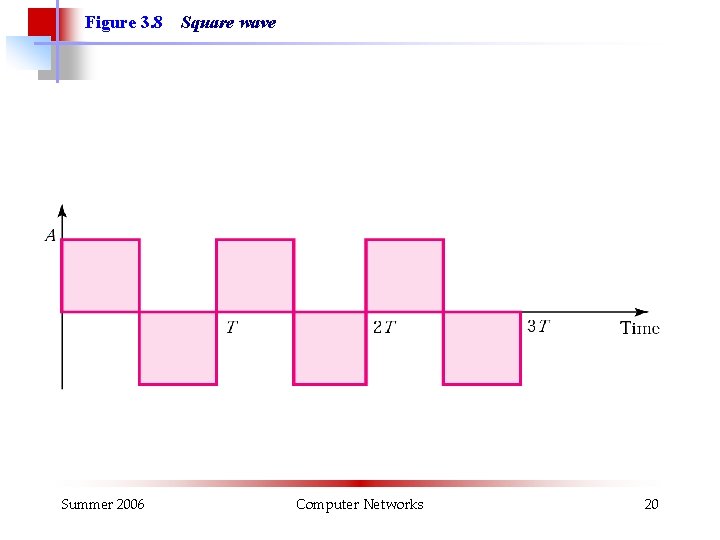
Figure 3. 8 Summer 2006 Square wave Computer Networks 20
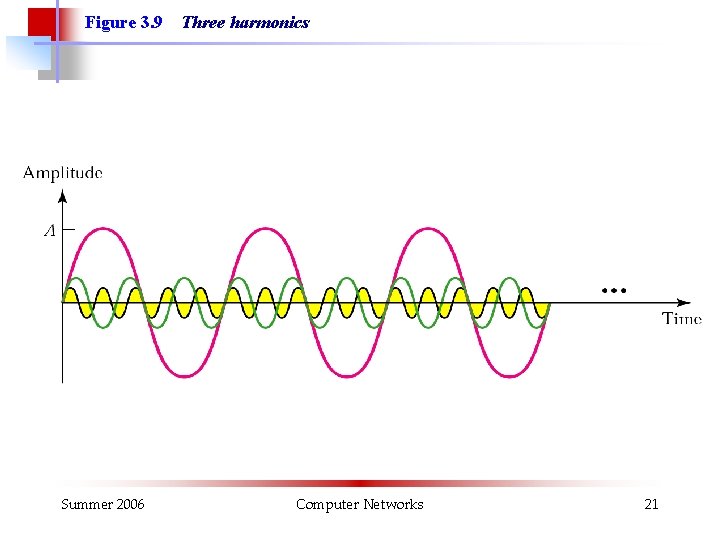
Figure 3. 9 Summer 2006 Three harmonics Computer Networks 21
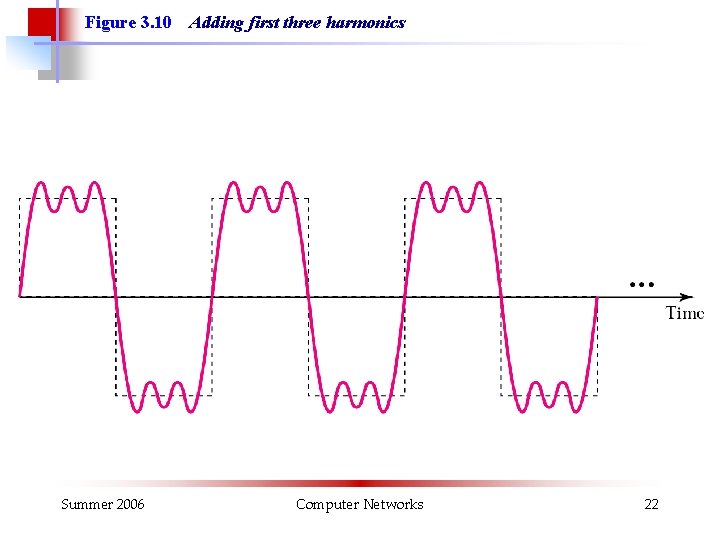
Figure 3. 10 Summer 2006 Adding first three harmonics Computer Networks 22

Figure 3. 11 Summer 2006 Frequency spectrum comparison Computer Networks 23
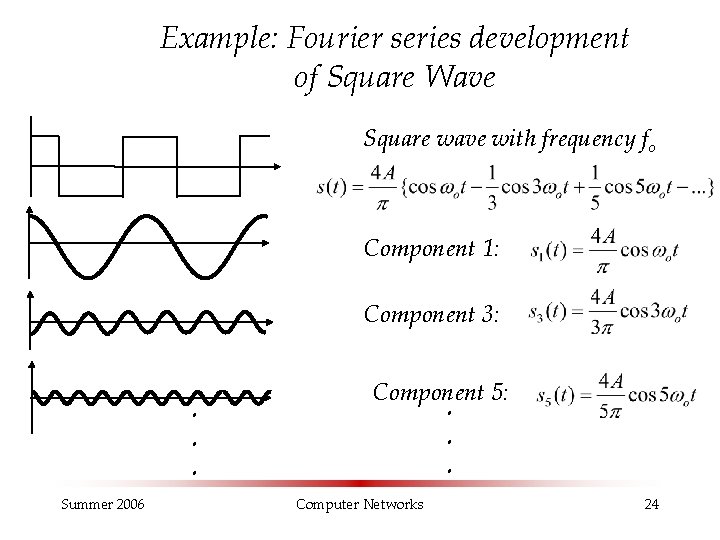
Example: Fourier series development of Square Wave Square wave with frequency fo Component 1: Component 3: . . . Summer 2006 Component 5: . . . Computer Networks 24

Characteristic of the Component Signals in the Square Wave § § Pulse wave with 50% duty cycle Infinite number of components Only the odd harmonic components are present The amplitudes of the components diminish with increasing frequency Summer 2006 Computer Networks 25
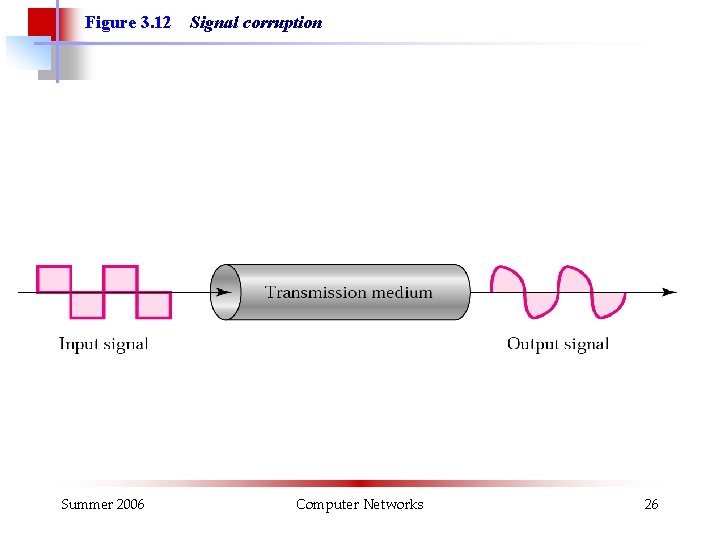
Figure 3. 12 Summer 2006 Signal corruption Computer Networks 26
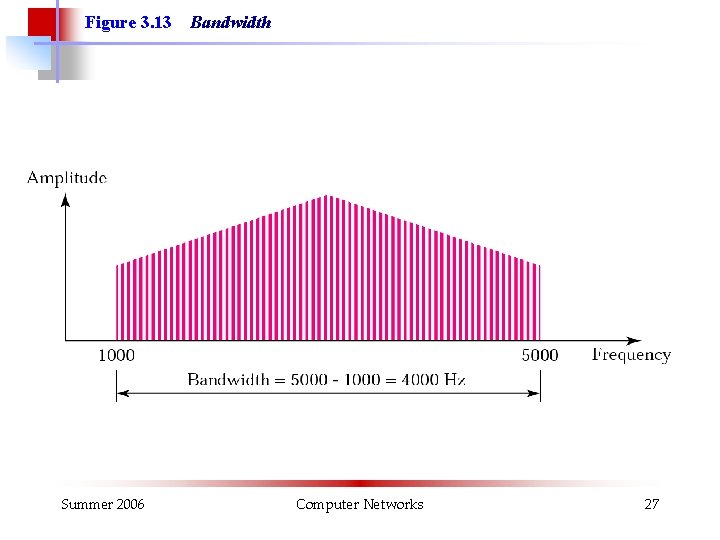
Figure 3. 13 Summer 2006 Bandwidth Computer Networks 27

Example 3 If a periodic signal is decomposed into five sine waves with frequencies of 100, 300, 500, 700, and 900 Hz, what is the bandwidth? Draw the spectrum, assuming all components have a maximum amplitude of 10 V. Solution B = fh - fl = 900 - 100 = 800 Hz The spectrum has only five spikes, at 100, 300, 500, 700, and 900 (see Figure 13. 4 ) Summer 2006 Computer Networks 28
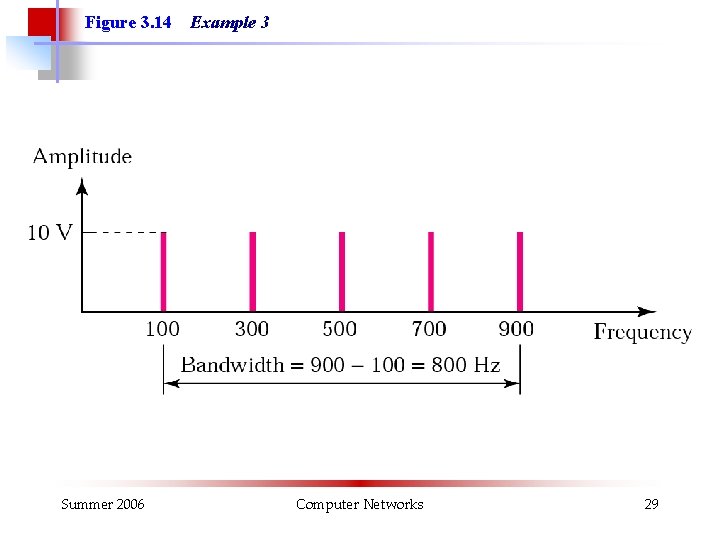
Figure 3. 14 Summer 2006 Example 3 Computer Networks 29

Example 5 A signal has a spectrum with frequencies between 1000 and 2000 Hz (bandwidth of 1000 Hz). A medium can pass frequencies from 3000 to 4000 Hz (a bandwidth of 1000 Hz). Can this signal faithfully pass through this medium? Solution The answer is definitely no. Although the signal can have the same bandwidth (1000 Hz), the range does not overlap. The medium can only pass the frequencies between 3000 and 4000 Hz; the signal is totally lost. Summer 2006 Computer Networks 30

Figure 3. 16 Summer 2006 A digital signal Computer Networks 31

Note: A digital signal is a composite signal with an infinite bandwidth. Summer 2006 Computer Networks 32
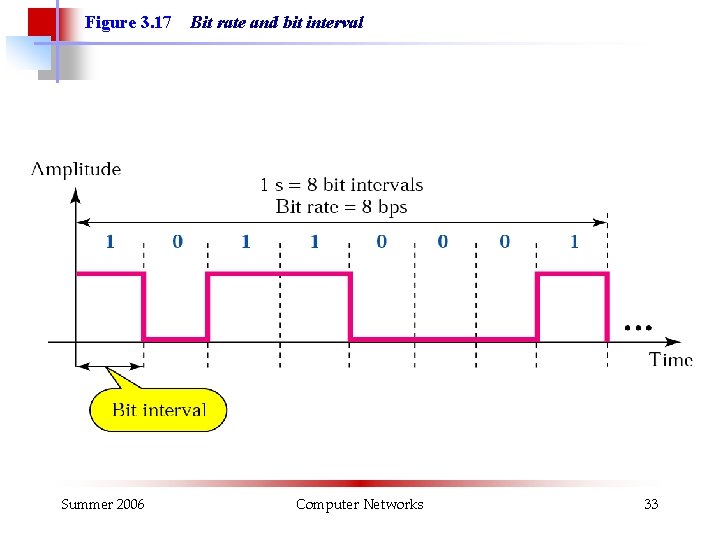
Figure 3. 17 Summer 2006 Bit rate and bit interval Computer Networks 33

Example 6 A digital signal has a bit rate of 2000 bps. What is the duration of each bit (bit interval) Solution The bit interval is the inverse of the bit rate. Bit interval = 1/ 2000 s = 0. 000500 x 106 ms = 500 ms Summer 2006 Computer Networks 34

Media Filters the Signal Media INPUT OUTPUT Certain frequencies do not pass through What happens when you limit frequencies? Square waves (digital values) lose their edges -> Harder to read correctly. Summer 2006 Computer Networks 35
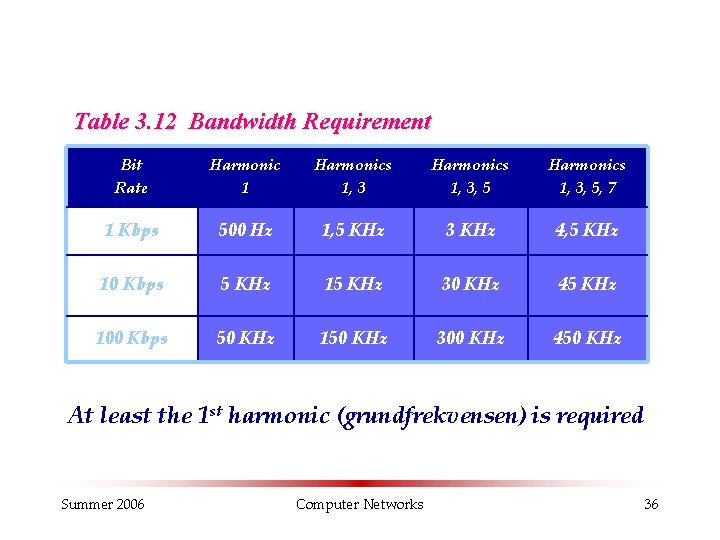
Table 3. 12 Bandwidth Requirement Bit Rate Harmonic 1 Harmonics 1, 3, 5, 7 1 Kbps 500 Hz 1, 5 KHz 3 KHz 4, 5 KHz 10 Kbps 5 KHz 15 KHz 30 KHz 45 KHz 100 Kbps 50 KHz 150 KHz 300 KHz 450 KHz At least the 1 st harmonic (grundfrekvensen) is required Summer 2006 Computer Networks 36

Note: The bit rate and the bandwidth are proportional to each other. Summer 2006 Computer Networks 37

Note: The analog bandwidth (signal bandwidht) of a medium is expressed in hertz; the digital bandwidth (data bandwidth), in bits per second. Summer 2006 Computer Networks 38

Note: Nyquist rule: The required bandwidth B is at least twice the pulse rate. Summer 2006 Computer Networks 39
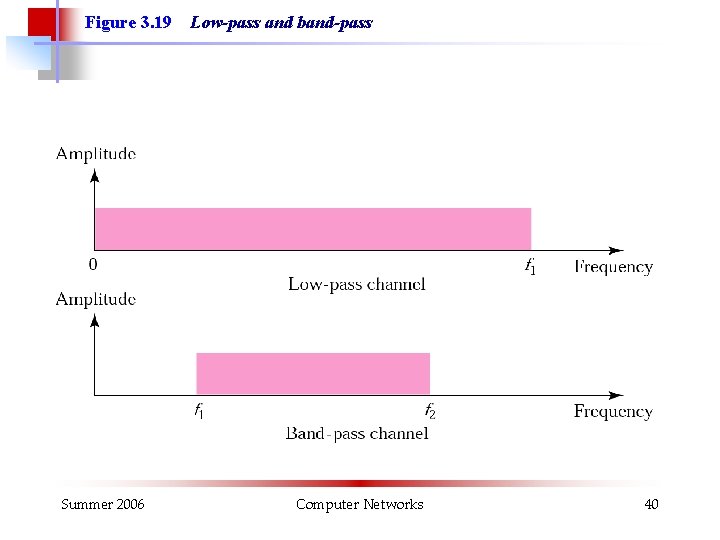
Figure 3. 19 Summer 2006 Low-pass and band-pass Computer Networks 40
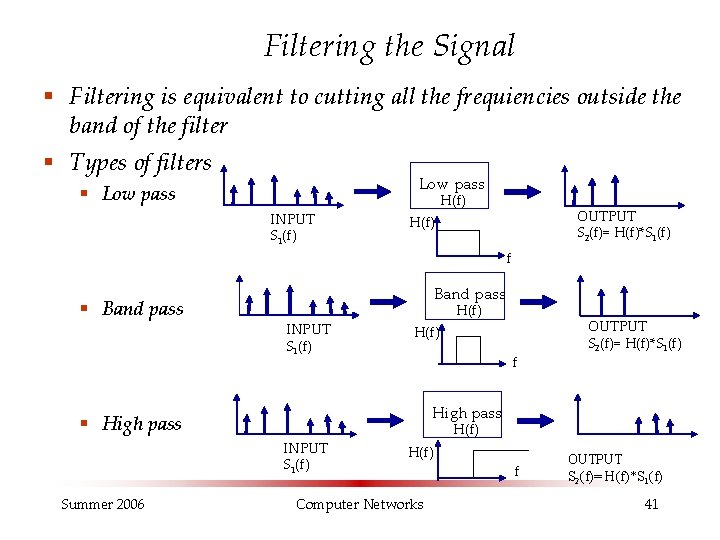
Filtering the Signal § Filtering is equivalent to cutting all the frequiencies outside the band of the filter § Types of filters Low pass § Low pass INPUT S 1(f) H(f) OUTPUT S 2(f)= H(f)*S 1(f) H(f) f § Band pass INPUT S 1(f) H(f) f High pass § High pass INPUT S 1(f) Summer 2006 OUTPUT S 2(f)= H(f)*S 1(f) H(f) Computer Networks f OUTPUT S 2(f)= H(f)*S 1(f) 41

Note: Digital transmission (pulse train without sine wave carrier modulation) needs a low-pass channel. In other books this is known as baseband digital transmission or line coding (digital-over-digital) Summer 2006 Computer Networks 42

Note: Analog transmission (by means of modulated sine wave carrier) can use a band-pass channel. If the number of waveforms is unlimited, this is called or passband analog tranmission (analog-over-analog). If the number of waveforms is limited, in other books, this is called digital passband digital transmission (digital-over-analog). Summer 2006 Computer Networks 43

Figure 3. 21 Summer 2006 Attenuation Computer Networks 44

Förstärkning mätt i decibel (d. B) 1 gång effektförstärkning = 0 d. B. 2 ggr effektförstärkning = 3 d. B. 10 ggr effektförstärkning = 10 d. B. 100 ggr effektförstärkning = 20 d. B. 1000 ggr effektförstärkning = 30 d. B. Osv. Summer 2006 Computer Networks 45

Dämpning mätt i decibel § Dämpning 100 ggr = Dämpning 20 d. B = förstärkning 0. 01 ggr = förstärkning med – 20 d. B. § Dämpning 1000 ggr = 30 d. B dämpning = -30 d. B förstärkning. § En halvering av signalen = dämpning med 3 d. B = förstärkning med -3 d. B. Summer 2006 Computer Networks 46

Measurement of Attenuation § Signal attenuation is measured in units called decibels (d. B). § If over a transmission link the ratio of output power is Po/Pi, the attenuation is said to be – 10 log 10(Po/Pi) = 10 log 10(Pi/Po) d. B. § In cascaded links the attenuation in d. B is simply a sum of the individual attenuations in d. B. § d. B is negative when the signal is attenuated and positive when the signal is amplified Summer 2006 Computer Networks 47

What is d. B? § A decibel is 1/10 th of a Bel, abbreviated d. B § Suppose a signal has a power of P 1 watts, and a second signal has a power of P 2 watts. Then the power amplitude difference in decibels, is: 10 log 10 (P 2 / P 1) § As a rule of thumb: 10 d. B means power ratio 10/1 20 d. B means power ratio 100/1 30 d. B means power ratio 1000/1 40 d. B means power ratio 10000/1 Summer 2006 Computer Networks 48

Example 12 Imagine a signal travels through a transmission medium and its power is reduced to half. This means that P 2 = 1/2 P 1. In this case, the attenuation (loss of power) can be calculated as Solution 10 log 10 (P 2/P 1) = 10 log 10 (0. 5 P 1/P 1) = 10 log 10 (0. 5) = 10(– 0. 3) = – 3 d. B Summer 2006 Computer Networks 49

Example 13 Imagine a signal travels through an amplifier and its power is increased ten times. This means that P 2 = 10· P 1. In this case, the amplification (gain of power) can be calculated as 10 log 10 (P 2/P 1) = 10 log 10 (10 P 1/P 1) = 10 log 10 (10) = 10 (1) = 10 d. B Summer 2006 Computer Networks 50
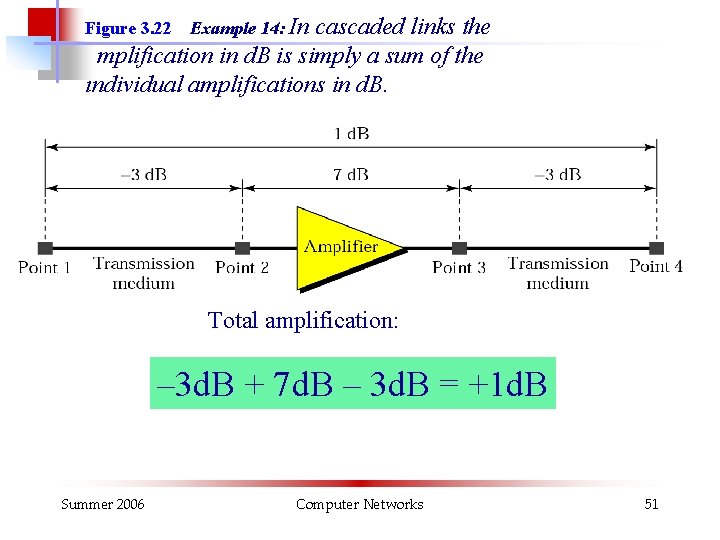
cascaded links the amplification in d. B is simply a sum of the individual amplifications in d. B. Figure 3. 22 Example 14: In Total amplification: – 3 d. B + 7 d. B – 3 d. B = +1 d. B Summer 2006 Computer Networks 51
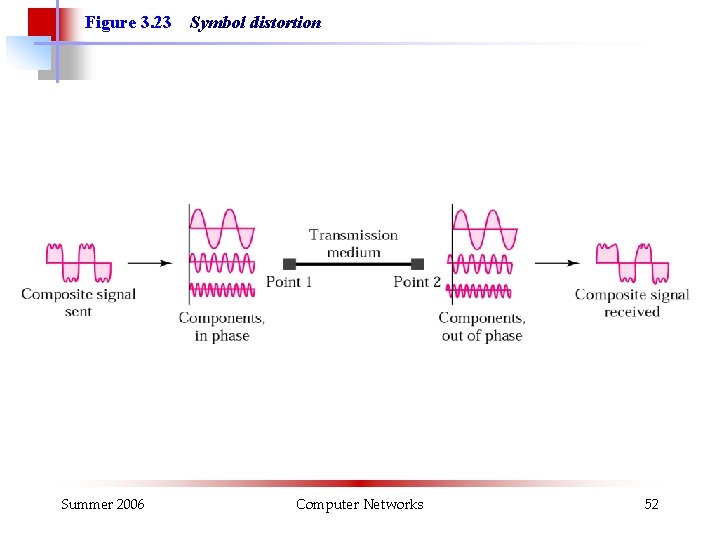
Figure 3. 23 Summer 2006 Symbol distortion Computer Networks 52
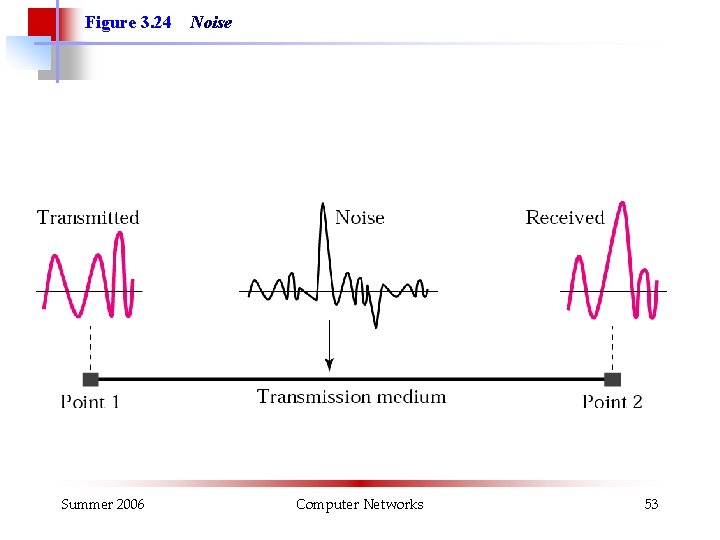
Figure 3. 24 Summer 2006 Noise Computer Networks 53
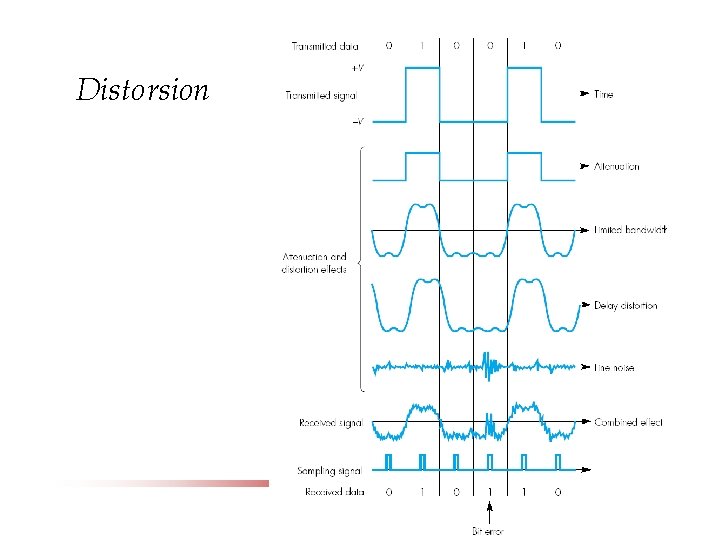
Distorsion
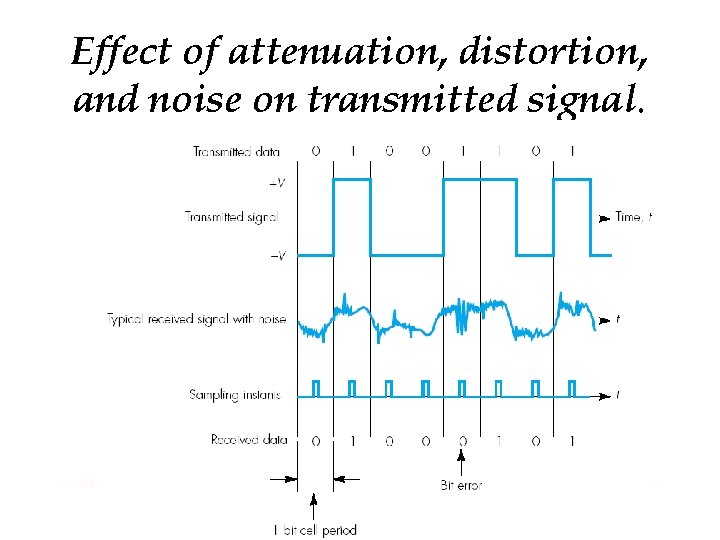
Effect of attenuation, distortion, and noise on transmitted signal.

Only for B level students

Gaussian noise Voltage Time

§ Only for B level Summer 2006 Computer Networks 58

Additive White Gaussian Noise (AWGN) channel § White noise = wideband (unfiltered) noise with constant noise density in Watt/Hertz = uncorrelated samples. § Pink noise = lowpass-filtered noise. § Additive = linear mixing. Signal + Noise source Noisy signal

Gaussian = Normal distribution Probability density funciton Matlab function: randn(Nsamples)*standarddev

Data sources are often simulated as random signals with Bernoulli distribution 0 1 1 0 0 1 0 Random sequence of independent 0: s and 1: s. Matlab function: rand(10)<0. 5

Bit error rate Example § Sent data: § Received data: § Bit error rate: 0101100011 0101110011

Bit error rate (BER) Example § Sent data: 0101100011 § Received data: 0 1 1 1 0 0 1 1 § Bit error rate: 10% § Bit error probablity: about 10%

Blockfelssannolikhet och bitfelssannolikhet där PB är blockfelssannolikhet, N är antal databitar per block och P är bitfelssannolikhet (nära Bit Error Rate, BER).

Example 1. 1

Answer
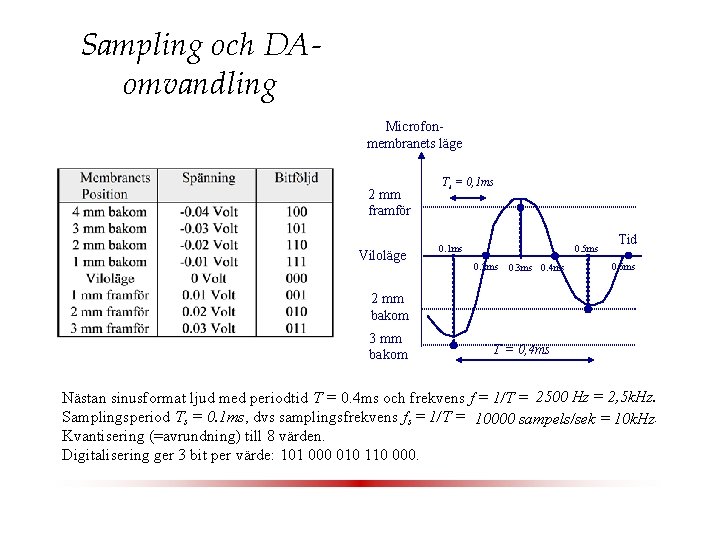
Sampling och DAomvandling Microfonmembranets läge 2 mm framför Viloläge Ts = 0, 1 ms 0. 5 ms 0. 2 ms 0. 3 ms 0. 4 ms Tid 0. 6 ms 2 mm bakom 3 mm bakom T = 0, 4 ms Nästan sinusformat ljud med periodtid T = 0. 4 ms och frekvens f = 1/T = 2500 Hz = 2, 5 k. Hz. Samplingsperiod Ts = 0. 1 ms, dvs samplingsfrekvens fs = 1/T = 10000 sampels/sek = 10 k. Hz. Kvantisering (=avrundning) till 8 värden. Digitalisering ger 3 bit per värde: 101 000 010 110 000.
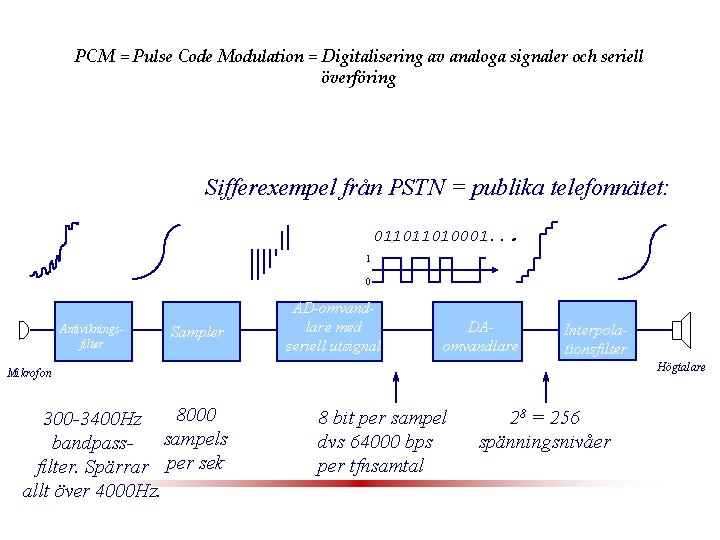
PCM = Pulse Code Modulation = Digitalisering av analoga signaler och seriell överföring Sifferexempel från PSTN = publika telefonnätet: 011011010001. . . 1 0 Antivikningsfilter Sampler AD-omvandlare med seriell utsignal DAomvandlare Interpolationsfilter Högtalare Mikrofon 8000 300 -3400 Hz bandpass- sampels filter. Spärrar per sek allt över 4000 Hz. 8 bit per sampel dvs 64000 bps per tfnsamtal 28 = 256 spänningsnivåer

Exempel En 6 sekunder lång ljudinspelning digitaliseras. Hur stor är inspelningens informationsmängd? a) 22000 sampels/sekund, 256 kvantiseringsnivåer. 22000 sampels * 6 s * 8 bit = 1056000 bit. b) 22000 sampels/sekund, 16 kvantiseringsnivåer. 22000 sampels * 6 s * 4 bit = 528000 bit. c) 5500 sampels/sekund, 256 kvantiseringsnivåer. 5500 sampels * 6 s * 8 bit = 264000 bit.

Vikningsdistorsion (aliasing) Inträffar om man inte filtrerar bort frekvenser som är högre än halva samplingsfrekvensen. Exempel: En sinuston på 4 k. Hz som samplas med samplingsfrekvens 4 kilosampels/s viks ned till en ton på 2 k. Hz.

Note: According to the Nyquist theorem, the sampling rate must be at least 2 times the highest frequency.

Samplingsteoremet § § § f < fs/2 Den högsta frekvens som kan samplas är halva samplingsfrekvensen. Om man samplar högre frekvens än fs/2 så byter signalen frekvens, dvs det uppstår vikningsdistorsion (aliasing). För att undvika vikningsdistorsion så har man ett anti-vikningsfilter innan samplingen, som tar bort frekvenser över halva samplingsfrekvensen. Interpolationsfiltret används vid rekonstruktion av den digitala signalen för att ”gissa” värden mellan samplen. Ett ideal interpolationsfilter skulle kunna återskapa den samplade signalen perfekt om den uppfyller samplingsteoremet. I verkligheten finns inga ideala filter. Följdregel: Nyqvist’s sats säger att max datahastighet = 2 B 2 log M, där M är antal nivåer, och B är signalens bandbredd, oftast lika med signalens övre gränsfrekvens.
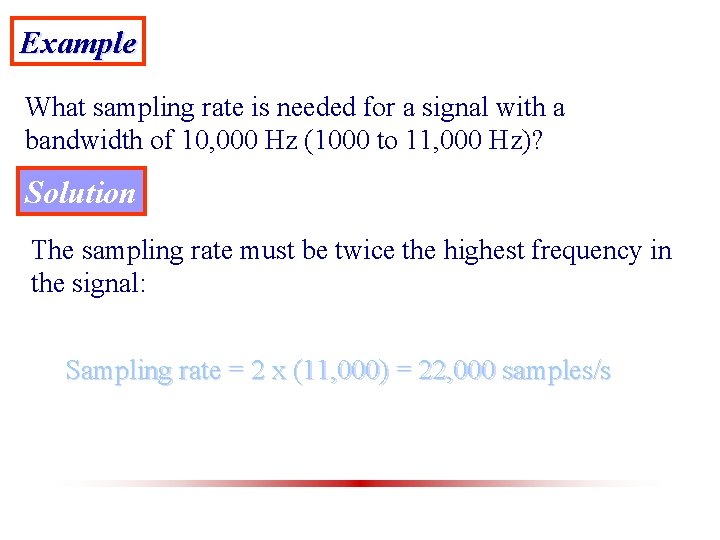
Example What sampling rate is needed for a signal with a bandwidth of 10, 000 Hz (1000 to 11, 000 Hz)? Solution The sampling rate must be twice the highest frequency in the signal: Sampling rate = 2 x (11, 000) = 22, 000 samples/s
- Slides: 73