Datorntverk A lektion 3 Kapitel 3 Fysiska signaler

Datornätverk A – lektion 3 §Kapitel 3: Fysiska signaler. §Kapitel 4: Digital transmission. Summer 2006 Computer Networks

Computer Networks Chapter 3 – Time and Frequency Domain Concept, Transmission Impairments Summer 2006 Computer Networks

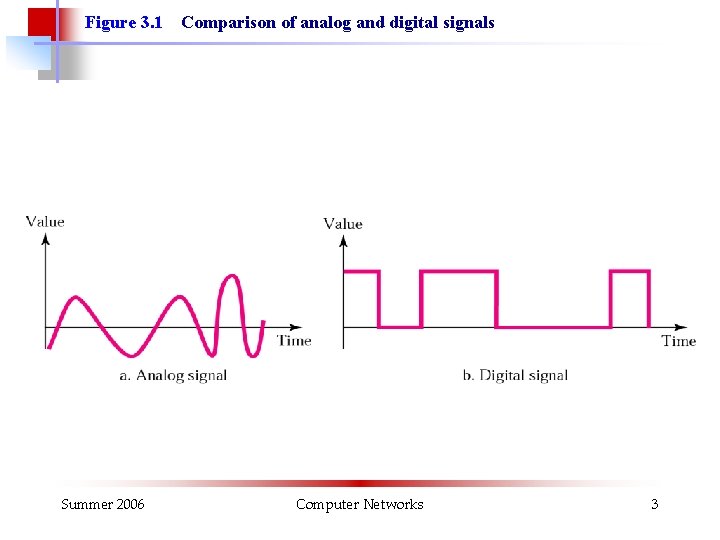
Figure 3. 1 Summer 2006 Comparison of analog and digital signals Computer Networks 3

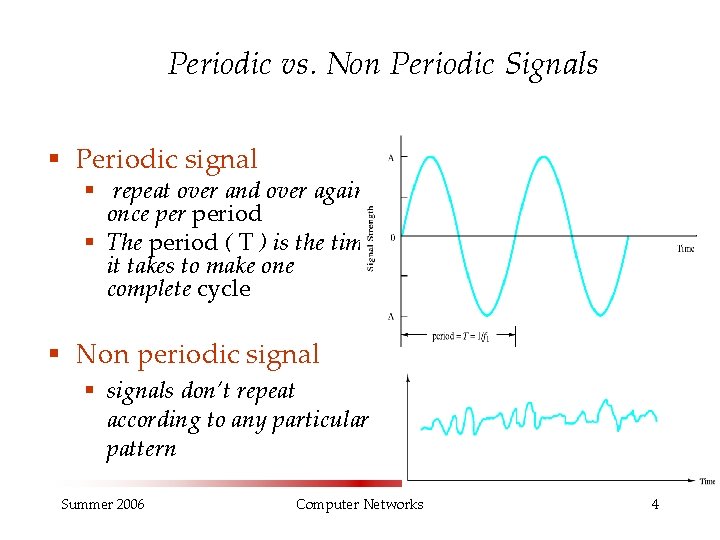
Periodic vs. Non Periodic Signals § Periodic signal § repeat over and over again, once period § The period ( T ) is the time it takes to make one complete cycle § Non periodic signal § signals don’t repeat according to any particular pattern Summer 2006 Computer Networks 4

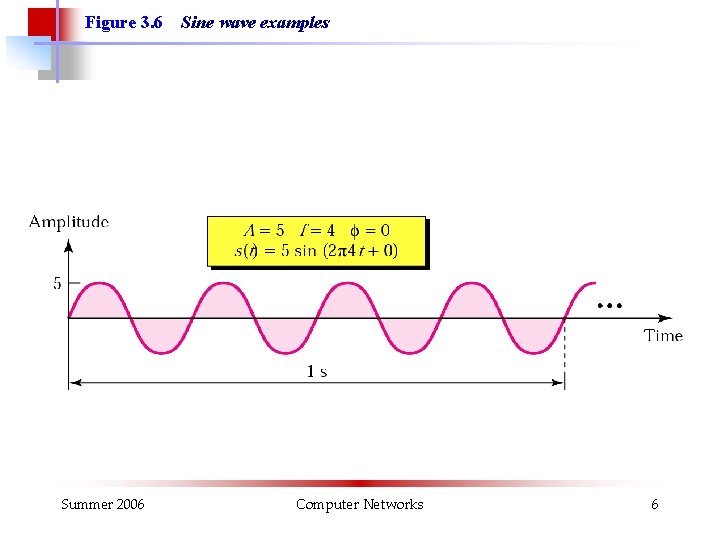
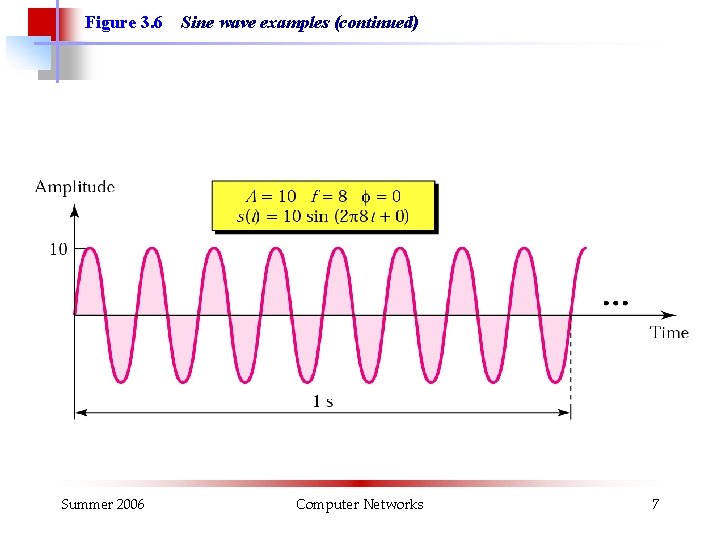
Sinusvågor Periodtid T = t 2 - t 1. Enhet: s. Frekvens f = 1/T. Enhet: 1/s=Hz. T=1/f. Amplitud eller toppvärde Û. Enhet: Volt. Fasläge: θ = 0 i ovanstående exempel. Enhet: Grader eller radianer. Momentan spänning: u(t)= Ûsin(2πft+θ) Summer 2006 Computer Networks 5

Figure 3. 6 Summer 2006 Sine wave examples Computer Networks 6

Figure 3. 6 Summer 2006 Sine wave examples (continued) Computer Networks 7

Tabell 3. 1 Enheter för periodtid och frekvens Enhet Sekunder (s) Ekvivalent 1 s Enhet Hertz (Hz) Ekvivalent 1 Hz Millisekunder (ms) 10– 3 s Kilohertz (k. Hz) 103 Hz Mikrosekunder (μs) 10– 6 s Megahertz (MHz) 106 Hz Nanosekunder (ns) 10– 9 s Gigahertz (GHz) 109 Hz Pikosekunder (ps) 10– 12 s Terahertz (THz) 1012 Hz Exempel: En sinusvåg med periodtid 1 ns har frekvens 1 GHz. Summer 2006 Computer Networks 8

Exempel Vilken frekvens i k. Hz har en sinusvåg med periodtid 100 ms? Lösning Alternativ 1: Gör om till grundenheten. 100 ms = 0. 1 s f = 1/0. 1 Hz = 10/1000 k. Hz = 0. 01 k. Hz Alternativ 2: Utnyttja att 1 ms motsvarar 1 k. Hz. f = 1/100 ms = 0. 01 k. Hz. Summer 2006 Computer Networks 9

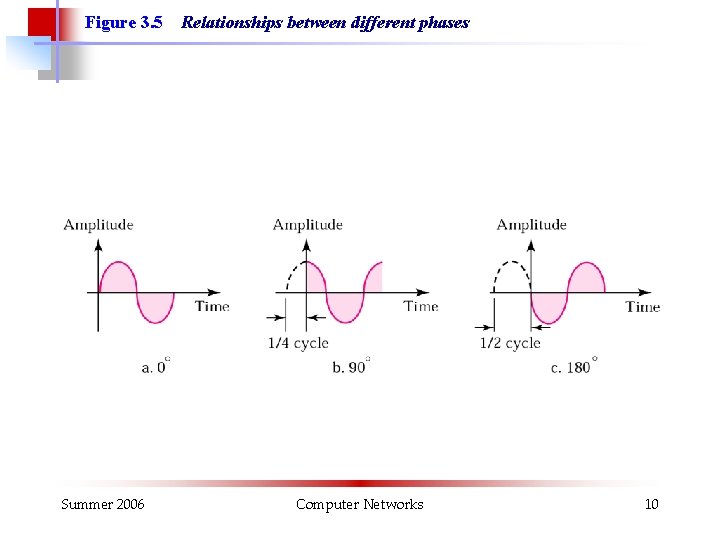
Figure 3. 5 Summer 2006 Relationships between different phases Computer Networks 10

Measuring the Phase § The phase is measured in degrees or in radians. § One full cycle is 360 o (degrees) = 2 p (radians) p 3. 14 Example: A sine wave is offset one-sixth of a cycle with respect to time 0. What is the phase in radians? Solution: (1/6) 360 = 60 degrees = 60 x 2 p /360 rad = 1. 046 rad Summer 2006 Computer Networks 11

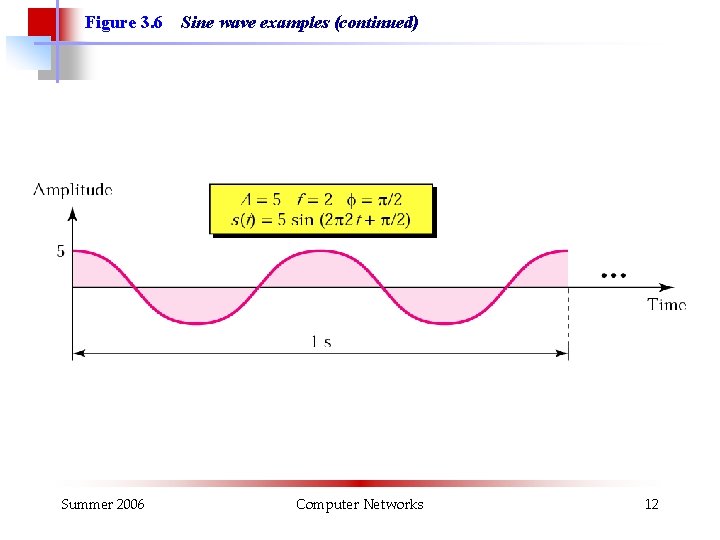
Figure 3. 6 Summer 2006 Sine wave examples (continued) Computer Networks 12

Example 2 A sine wave is offset one-sixth of a cycle with respect to time zero. What is its phase in degrees and radians? Solution We know that one complete cycle is 360 degrees. Therefore, 1/6 cycle is (1/6) 360 = 60 degrees = 60 x 2 p /360 rad = 1. 046 rad Summer 2006 Computer Networks 13

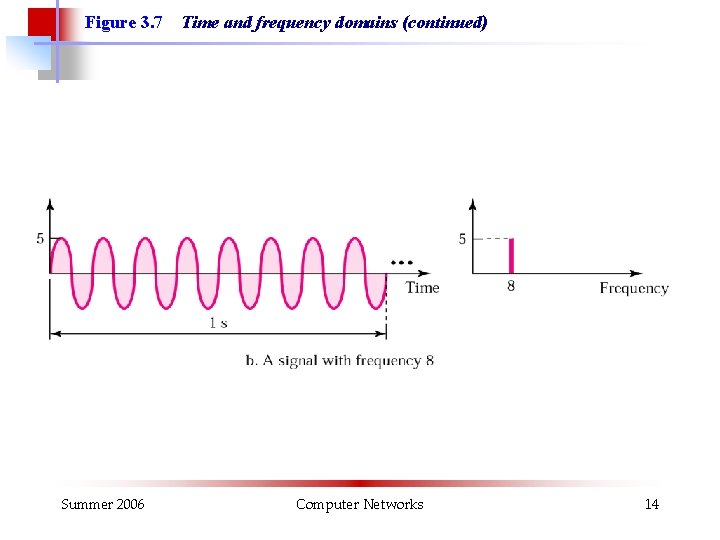
Figure 3. 7 Summer 2006 Time and frequency domains (continued) Computer Networks 14

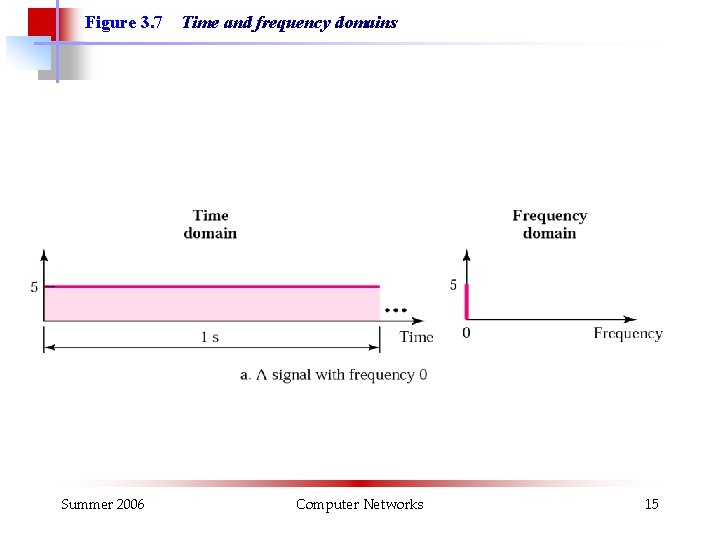
Figure 3. 7 Summer 2006 Time and frequency domains Computer Networks 15

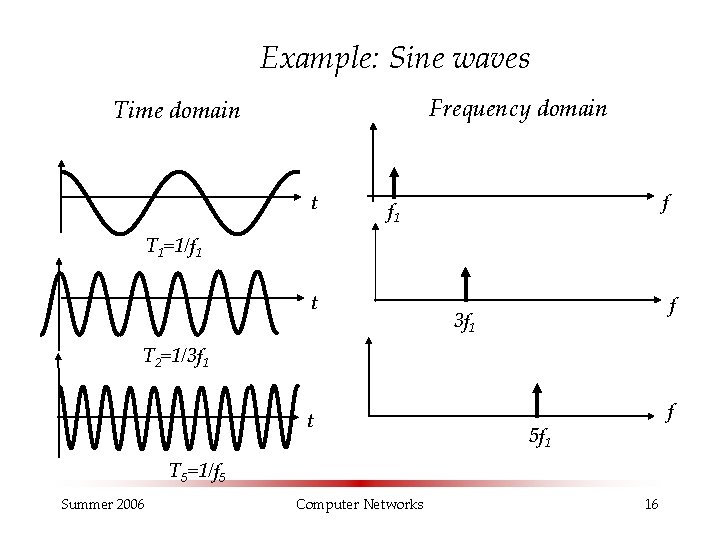
Example: Sine waves Frequency domain Time domain t f f 1 T 1=1/f 1 t f 3 f 1 T 2=1/3 f 1 t f 5 f 1 T 5=1/f 5 Summer 2006 Computer Networks 16

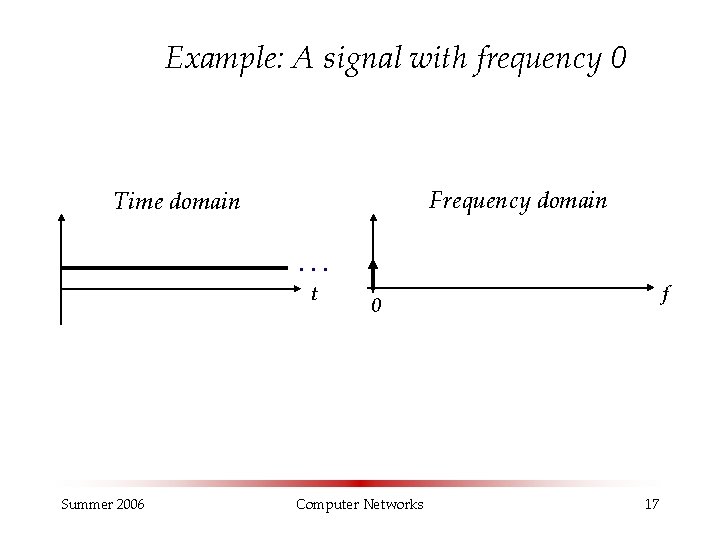
Example: A signal with frequency 0 Frequency domain Time domain. . . t Summer 2006 f 0 Computer Networks 17

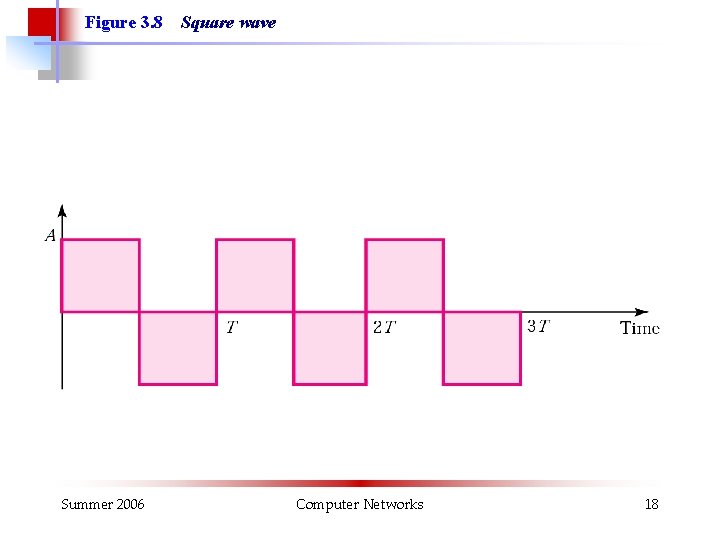
Figure 3. 8 Summer 2006 Square wave Computer Networks 18

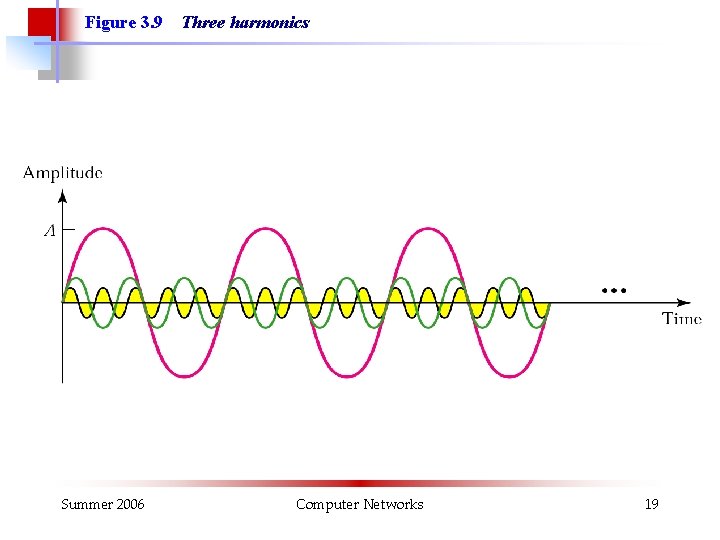
Figure 3. 9 Summer 2006 Three harmonics Computer Networks 19

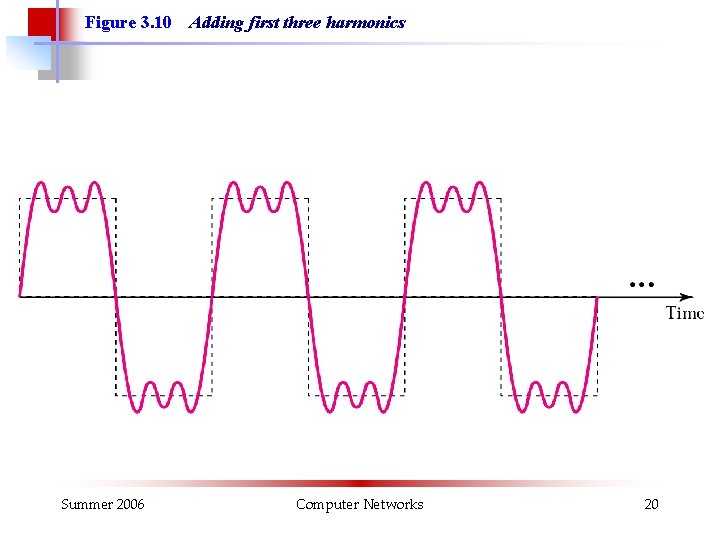
Figure 3. 10 Summer 2006 Adding first three harmonics Computer Networks 20

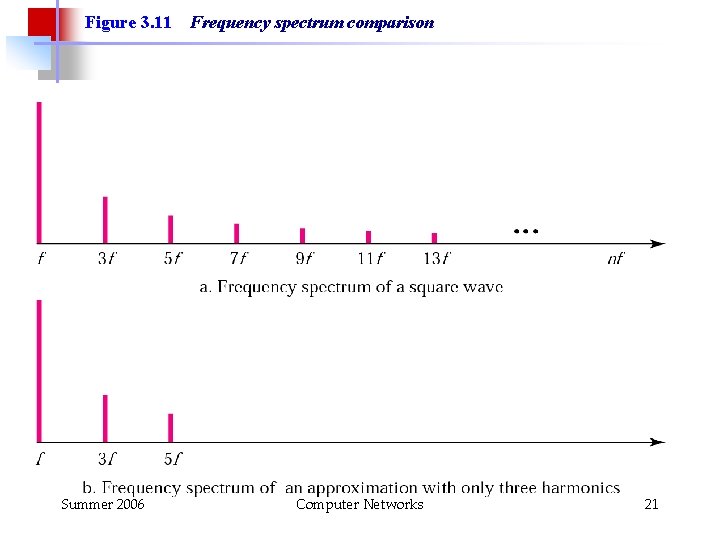
Figure 3. 11 Summer 2006 Frequency spectrum comparison Computer Networks 21

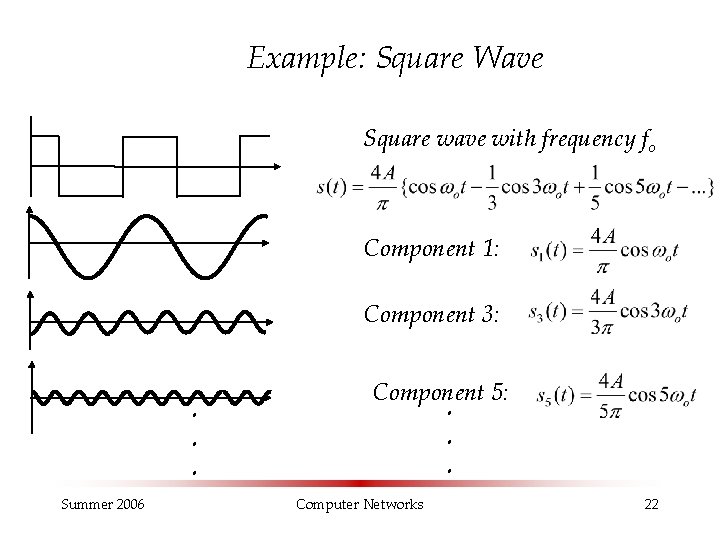
Example: Square Wave Square wave with frequency fo Component 1: Component 3: . . . Summer 2006 Component 5: . . . Computer Networks 22

Characteristic of the Component Signals in the Square Wave § Infinite number of components § Only the odd harmonic components are present § The amplitudes of the components diminish with increasing frequency Summer 2006 Computer Networks 23

Examples 1. If digital signal has bit rate of 2000 bps, what is the duration of each bit? bit interval = 1/2000 = 0. 0005 = 500 ms 2. If a digital signal has a bit interval of 400 ns, what is the bit rate? bit rate = 1/(400 · 10 -9) = 25 · 106 = 25 Mbps Summer 2006 Computer Networks 24

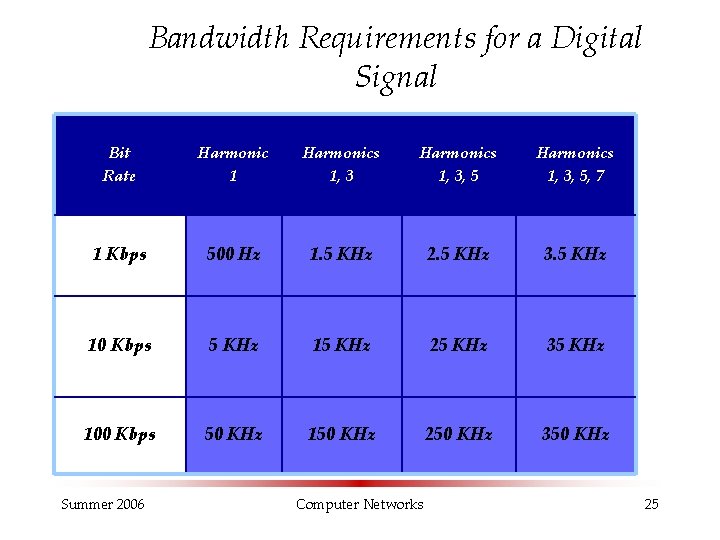
Bandwidth Requirements for a Digital Signal Bit Rate Harmonic 1 Harmonics 1, 3, 5, 7 1 Kbps 500 Hz 1. 5 KHz 2. 5 KHz 3. 5 KHz 10 Kbps 5 KHz 15 KHz 25 KHz 35 KHz 100 Kbps 50 KHz 150 KHz 250 KHz 350 KHz Summer 2006 Computer Networks 25

Figure 3. 12 Summer 2006 Signal corruption Computer Networks 26

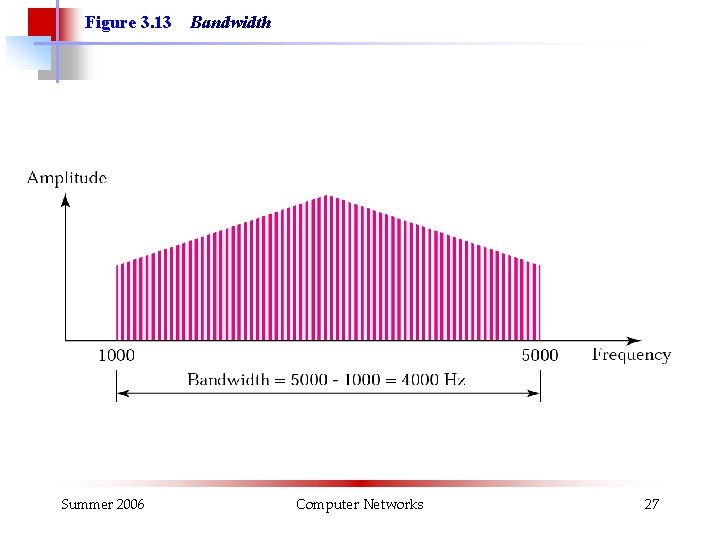
Figure 3. 13 Summer 2006 Bandwidth Computer Networks 27

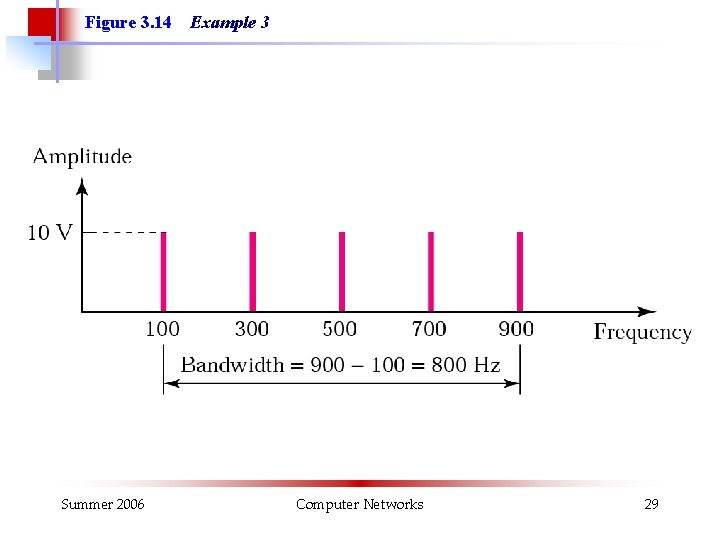
Example 3 If a periodic signal is decomposed into five sine waves with frequencies of 100, 300, 500, 700, and 900 Hz, what is the bandwidth? Draw the spectrum, assuming all components have a maximum amplitude of 10 V. Solution B = fh - fl = 900 - 100 = 800 Hz The spectrum has only five spikes, at 100, 300, 500, 700, and 900 (see Figure 13. 4 ) Summer 2006 Computer Networks 28

Figure 3. 14 Summer 2006 Example 3 Computer Networks 29

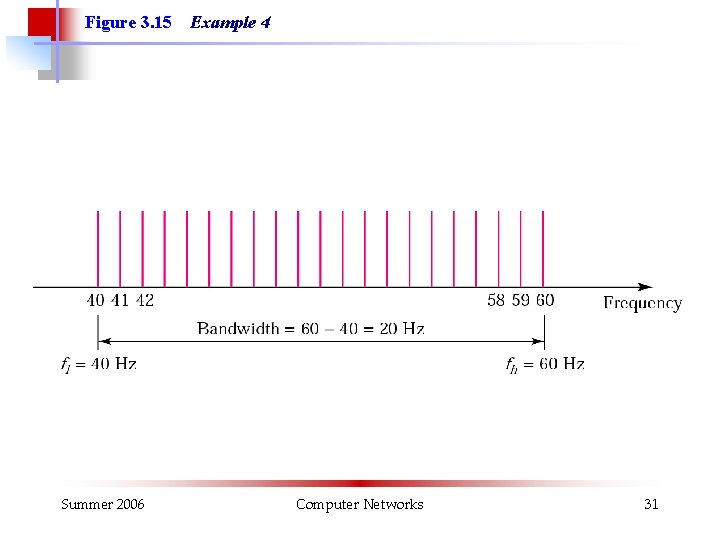
Example 4 A signal has a bandwidth of 20 Hz. The highest frequency is 60 Hz. What is the lowest frequency? Draw the spectrum if the signal contains all integral frequencies of the same amplitude. Solution B = fh - fl 20 = 60 - fl fl = 60 - 20 = 40 Hz Summer 2006 Computer Networks 30

Figure 3. 15 Summer 2006 Example 4 Computer Networks 31

Example 5 A signal has a spectrum with frequencies between 1000 and 2000 Hz (bandwidth of 1000 Hz). A medium can pass frequencies from 3000 to 4000 Hz (a bandwidth of 1000 Hz). Can this signal faithfully pass through this medium? Solution The answer is definitely no. Although the signal can have the same bandwidth (1000 Hz), the range does not overlap. The medium can only pass the frequencies between 3000 and 4000 Hz; the signal is totally lost. Summer 2006 Computer Networks 32

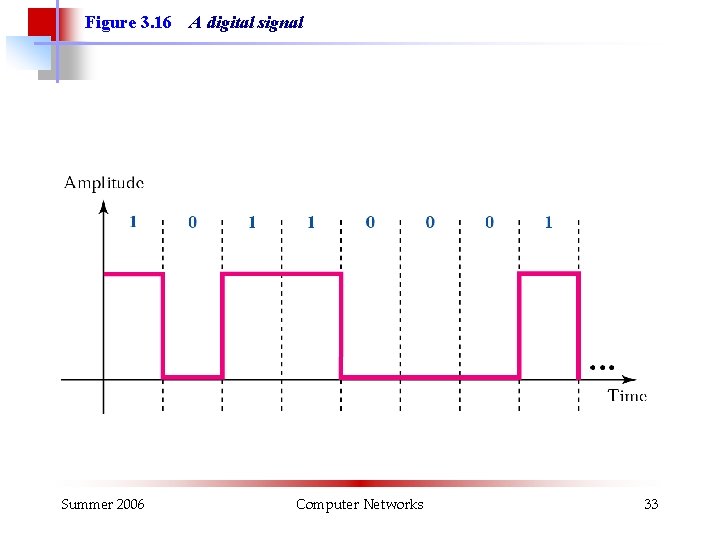
Figure 3. 16 Summer 2006 A digital signal Computer Networks 33

Note: A digital signal is a composite signal with an infinite bandwidth. Summer 2006 Computer Networks 34

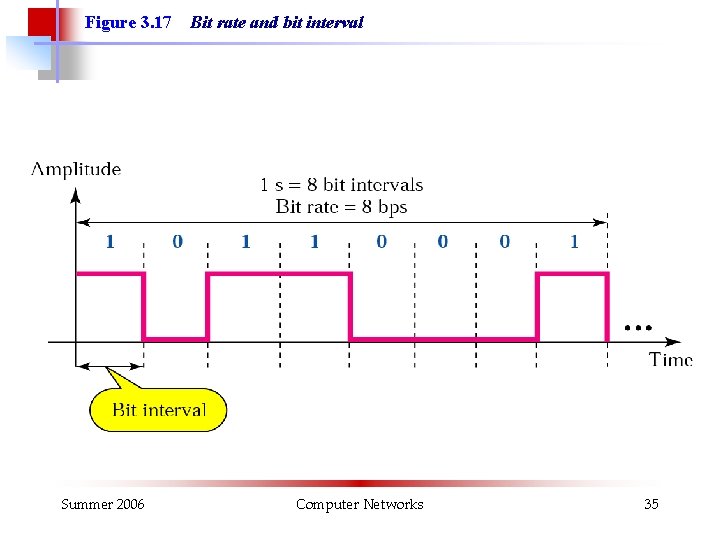
Figure 3. 17 Summer 2006 Bit rate and bit interval Computer Networks 35

Example 6 A digital signal has a bit rate of 2000 bps. What is the duration of each bit (bit interval) Solution The bit interval is the inverse of the bit rate. Bit interval = 1/ 2000 s = 0. 000500 x 106 ms = 500 ms Summer 2006 Computer Networks 36

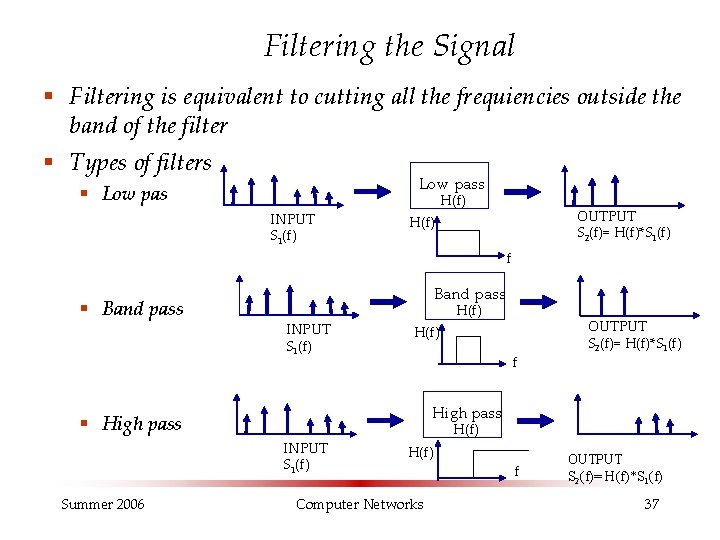
Filtering the Signal § Filtering is equivalent to cutting all the frequiencies outside the band of the filter § Types of filters Low pass § Low pas INPUT S 1(f) H(f) OUTPUT S 2(f)= H(f)*S 1(f) H(f) f § Band pass INPUT S 1(f) H(f) f High pass § High pass INPUT S 1(f) Summer 2006 OUTPUT S 2(f)= H(f)*S 1(f) H(f) Computer Networks f OUTPUT S 2(f)= H(f)*S 1(f) 37

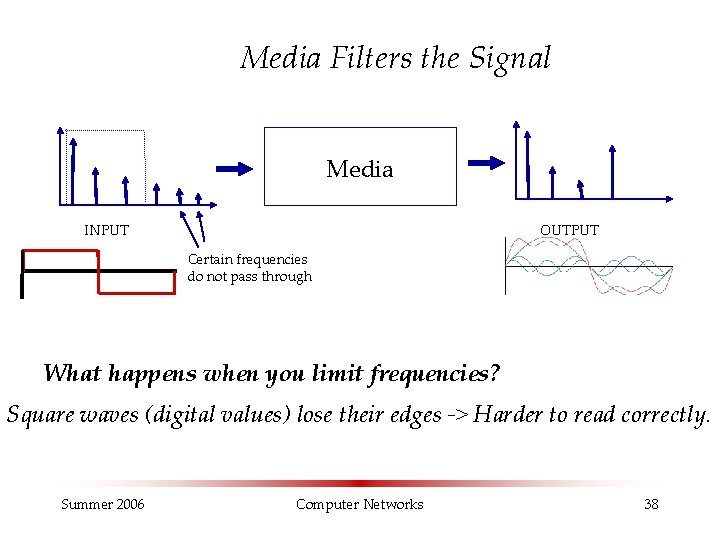
Media Filters the Signal Media INPUT OUTPUT Certain frequencies do not pass through What happens when you limit frequencies? Square waves (digital values) lose their edges -> Harder to read correctly. Summer 2006 Computer Networks 38

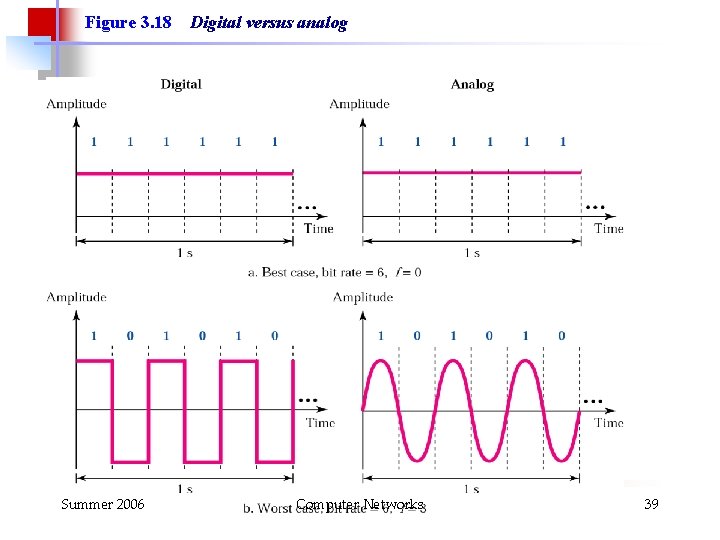
Figure 3. 18 Summer 2006 Digital versus analog Computer Networks 39

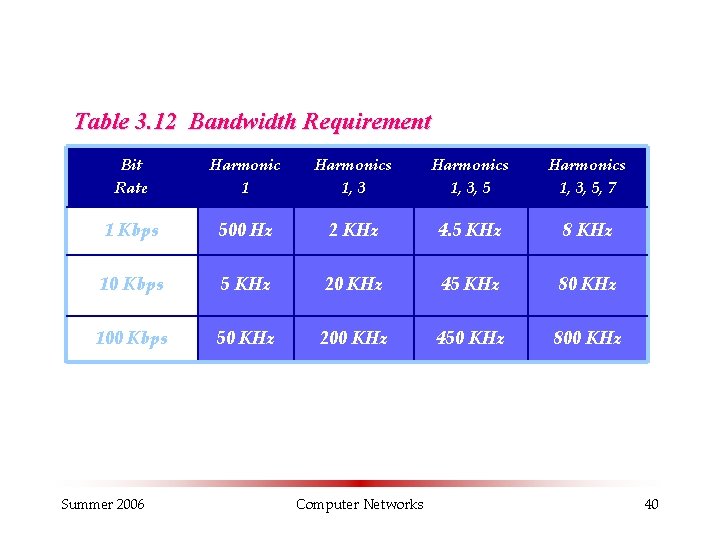
Table 3. 12 Bandwidth Requirement Bit Rate Harmonic 1 Harmonics 1, 3, 5, 7 1 Kbps 500 Hz 2 KHz 4. 5 KHz 8 KHz 10 Kbps 5 KHz 20 KHz 45 KHz 80 KHz 100 Kbps 50 KHz 200 KHz 450 KHz 800 KHz Summer 2006 Computer Networks 40

Note: The bit rate and the bandwidth are proportional to each other. Summer 2006 Computer Networks 41

Note: The analog bandwidth of a medium is expressed in hertz; the digital bandwidth, in bits per second. Summer 2006 Computer Networks 42

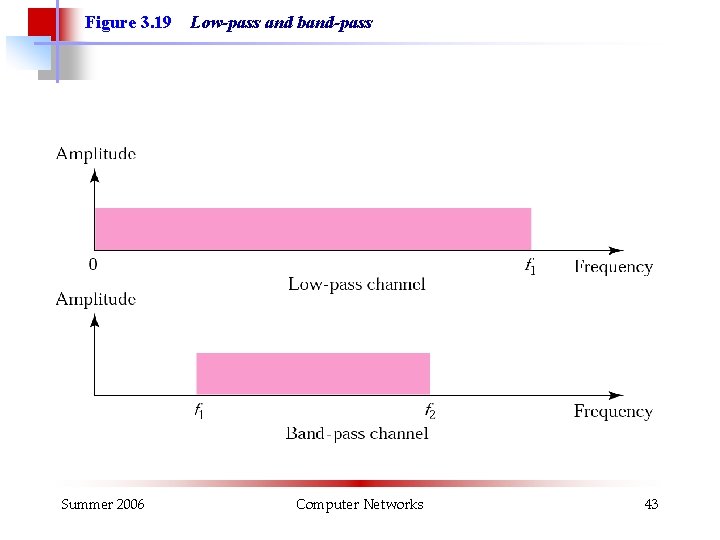
Figure 3. 19 Summer 2006 Low-pass and band-pass Computer Networks 43

Note: Digital transmission needs a low-pass channel. Summer 2006 Computer Networks 44

Note: Analog transmission can use a bandpass channel. Summer 2006 Computer Networks 45

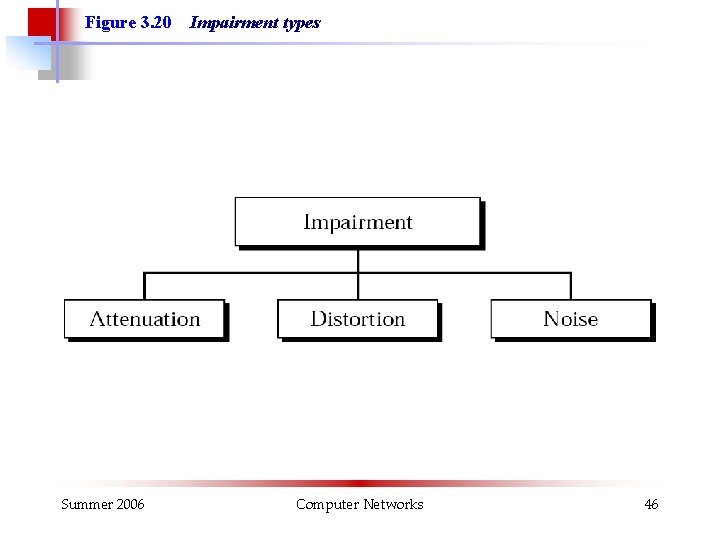
Figure 3. 20 Summer 2006 Impairment types Computer Networks 46

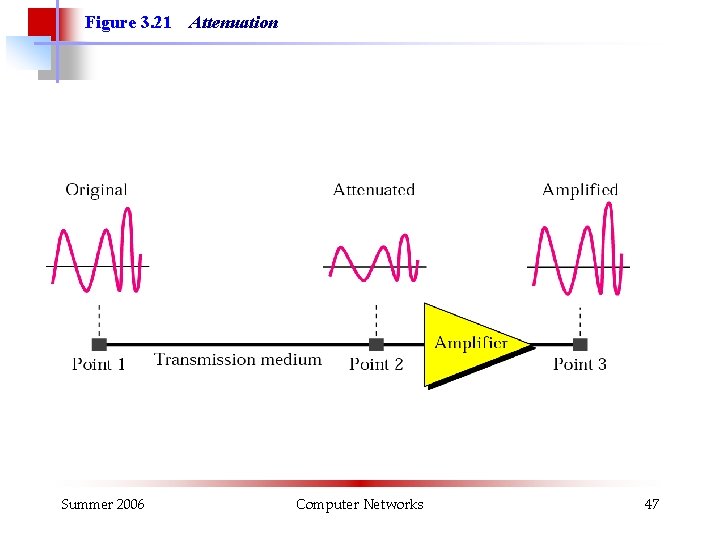
Figure 3. 21 Summer 2006 Attenuation Computer Networks 47

Förstärkning mätt i decibel (d. B) 1 gång effektförstärkning = 0 d. B. 2 ggr effektförstärkning = 3 d. B. 10 ggr effektförstärkning = 10 d. B. 100 ggr effektförstärkning = 20 d. B. 1000 ggr effektförstärkning = 30 d. B. Osv. Summer 2006 Computer Networks 48

Dämpning mätt i decibel § Dämpning 100 ggr = Dämpning 20 d. B = förstärkning 0. 01 ggr = förstärkning med – 20 d. B. § Dämpning 1000 ggr = 30 d. B dämpning = -30 d. B förstärkning. § En halvering av signalen = dämpning med 3 d. B = förstärkning med -3 d. B. Summer 2006 Computer Networks 49

Measurement of Attenuation § Signal attenuation is measured in units called decibels (d. B). § If over a transmission link the ratio of output power is Po/Pi, the attenuation is said to be – 10 log 10(Po/Pi) = 10 log 10(Pi/Po) d. B. § In cascaded links the attenuation in d. B is simply a sum of the individual attenuations in d. B. § d. B is negative when the signal is attenuated and positive when the signal is amplified Summer 2006 Computer Networks 50

What is d. B? § A decibel is 1/10 th of a Bel, abbreviated d. B § Suppose a signal has a power of P 1 watts, and a second signal has a power of P 2 watts. Then the power amplitude difference in decibels, symbolized Sd. BP, is: Sd. BP = 10 log 10 (P 2 / P 1) § As a rule of thumb: S/N ratio of 10 d. B means 10/1 S/N ratio of 20 d. B means 100/1 S/N ratio of 30 d. B means 1000/1 S/N ratio of 40 d. B means 10000/1 Summer 2006 Computer Networks 51

Examples: 1. A signal that travels through a transmission medium is reduced to half. This means that P 2 = (1/2)P 1 The attenuation can be calculated as follows: 10 log 10(P 2/P 1)=10 log 10 (0. 5 P 1/P 1)=10 log 10 (0. 5)= -3 d. B 2. Imagine a signal goes through an amplifier and its power is increased 10 times. This means that P 2 = 10 P 1 The amplification is: 10 log 10 (10 P 1/P 1)= =10 log 1010=10 d. B Summer 2006 Computer Networks 52

Example 12 Imagine a signal travels through a transmission medium and its power is reduced to half. This means that P 2 = 1/2 P 1. In this case, the attenuation (loss of power) can be calculated as Solution 10 log 10 (P 2/P 1) = 10 log 10 (0. 5 P 1/P 1) = 10 log 10 (0. 5) = 10(– 0. 3) = – 3 d. B Summer 2006 Computer Networks 53

Example 13 Imagine a signal travels through an amplifier and its power is increased ten times. This means that P 2 = 10 ¥ P 1. In this case, the amplification (gain of power) can be calculated as 10 log 10 (P 2/P 1) = 10 log 10 (10 P 1/P 1) = 10 log 10 (10) = 10 (1) = 10 d. B Summer 2006 Computer Networks 54

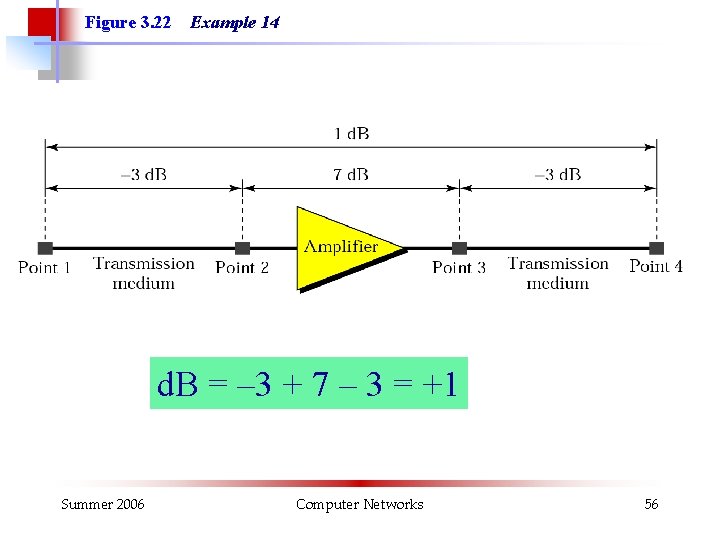
Example 14 One reason that engineers use the decibel to measure the changes in the strength of a signal is that decibel numbers can be added (or subtracted) when we are talking about several points instead of just two (cascading). In Figure 3. 22 a signal travels a long distance from point 1 to point 4. The signal is attenuated by the time it reaches point 2. Between points 2 and 3, the signal is amplified. Again, between points 3 and 4, the signal is attenuated. We can find the resultant decibel for the signal just by adding the decibel measurements between each set of points. Summer 2006 Computer Networks 55

Figure 3. 22 Example 14 d. B = – 3 + 7 – 3 = +1 Summer 2006 Computer Networks 56

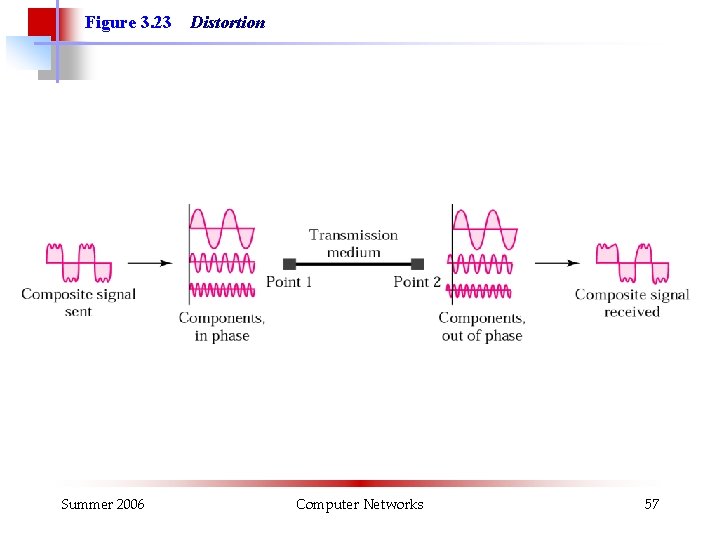
Figure 3. 23 Summer 2006 Distortion Computer Networks 57

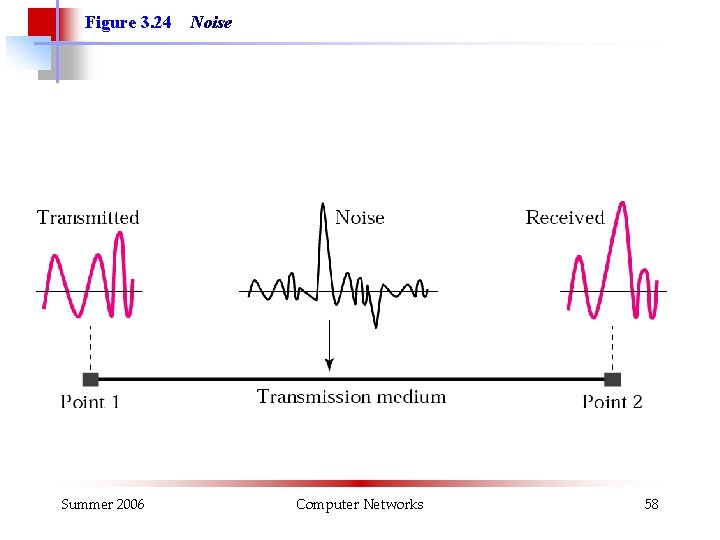
Figure 3. 24 Summer 2006 Noise Computer Networks 58

Noise and Interference § Noise is present in the form of random motion of electrons in conductors, devices and electronic systems (due to thermal energy) and can be also picked up from external sources (atmospheric disturbances, ignition noise etc. ) § Interference (cross-talk) generally refers to the unwanted signals, picked up by communication link due to other transmissions taking place in adjacent frequency bands or in physically adjacent transmission lines Summer 2006 Computer Networks 59

Signal-brus-förhållande § Ett signal-brus-förhållande på 100 d. B innebär att den starkaste signalen är 100 d. B starkare än bruset. § Ljud som är svagare än bruset hörs inte utan dränks i bruset. § Ljudets dynamik skillnaden mellan den starkaste ljudet och det svagaste ljudet som man kan höra, och är vanligen ungefär detsamma som signalbrus-förhållandet. Summer 2006 Computer Networks 60

Summer 2006 Computer Networks 61

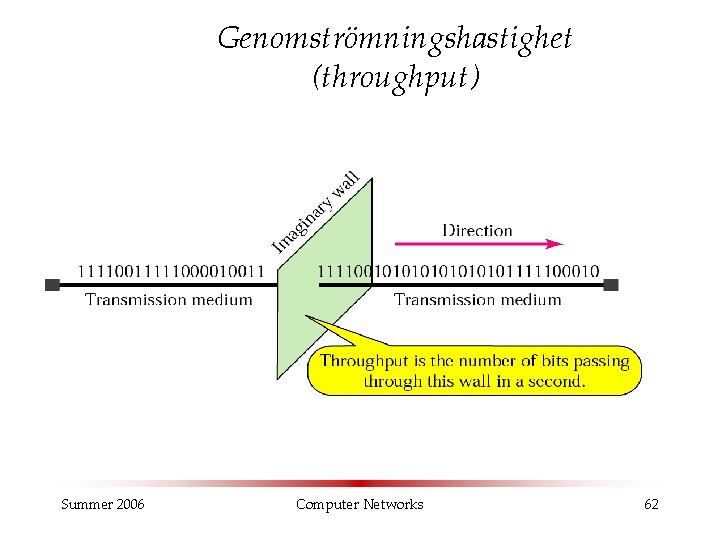
Genomströmningshastighet (throughput) Summer 2006 Computer Networks 62

Figure 3. 26 Summer 2006 Propagation time Computer Networks 63

Delay (Time, Latency) § When data are sent from one point to the other point (without intermediate points), two types of delays are experienced: § transmission delay (time) § propagation delay (time) § When data pass through intermediate points four types of delay (latency) are experienced: § § transmission delay (time) propagation delay (time) queue time processing time Summer 2006 Computer Networks 64

Transmission Delay (Time) § The transmission time is the time necessary to put the message on the link (chanel). § The transmission time depends on the length of the message and the throughput (bit rate) of the link and is expressed as: length of message (bits) bit rate (bits/sec) Summer 2006 Computer Networks 65

Propagation Delay (Time) § The propagation delay is the time needed for the signal to propagate (travel) from one end of a channel to the other. § The transmition time depends on the distance between the two ends and the speed of the signal and is expressed as distance (m) / speed of propagation (m/s) § Through free space signals propagate at the speed of light which is 3 * 108 m/s § Through wires signals propagate at the speed of 2 * 108 m/s Summer 2006 Computer Networks 66

Queue and Processing time § Queue time § When the intermediate nodes are busy processing other data, the data arrived at the node are queued. Queue time is the time spent waiting in the queue. § Processing time § This is the time needed for the data to be processed at the intermediate nodes. Summer 2006 Computer Networks 67