Dates for term tests 1 Friday February 5

Dates for term tests 1. Friday, February 5 2. Friday, March 5 3. Friday, March 26

The Moving Average Time series of order q, MA(q) Let {xt|t T} be defined by the equation. where {ut|t T} denote a white noise time series with variance s 2. Then {xt|t T} is called a Moving Average time series of order q. (denoted by MA(q))

The mean value for an MA(q) time series The autocovariance function for an MA(q) time series The autocorrelation function for an MA(q) time series

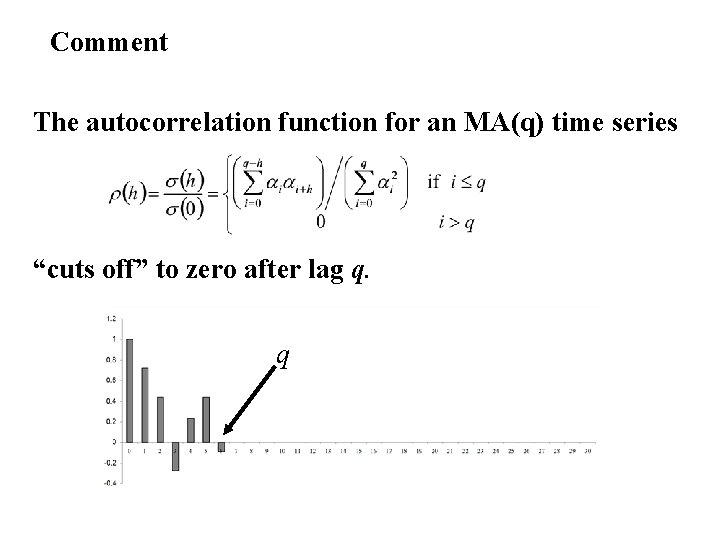
Comment The autocorrelation function for an MA(q) time series “cuts off” to zero after lag q. q

The Autoregressive Time series of order p, AR(p) Let {xt|t T} be defined by the equation. where {ut|t T} is a white noise time series with variance s 2. Then {xt|t T} is called a Autoregressive time series of order p. (denoted by AR(p))

The mean value of a stationary AR(p) series The Autocovariance function s(h) of a stationary AR(p) series Satisfies the equations:

The Autocorrelation function r(h) of a stationary AR(p) series Satisfies the equations: with for h > p and

or: where r 1, r 2, … , rp are the roots of the polynomial and c 1, c 2, … , cp are determined by using the starting values of the sequence r(h).

Conditions for stationarity Autoregressive Time series of order p, AR(p)

If b 1 = 1 and d = 0. The value of xt increases in magnitude and ut eventually becomes negligible. The time series {xt|t T} satisfies the equation: The time series {xt|t T} exhibits deterministic behaviour.

For a AR(p) time series, consider the polynomial with roots r 1, r 2 , … , rp then {xt|t T} is stationary if |ri| > 1 for all i. If |ri| < 1 for at least one i then {xt|t T} exhibits deterministic behaviour. If |ri| ≥ 1 and |ri| = 1 for at least one i then {xt|t T} exhibits non-stationary random behaviour.

since: and |r 1 |>1, |r 2 |>1, … , | rp | > 1 for a stationary AR(p) series then i. e. the autocorrelation function, r(h), of a stationary AR(p) series “tails off” to zero.

Special Cases: The AR(1) time Let {xt|t T} be defined by the equation.

Consider the polynomial with root r 1= 1/b 1 1. {xt|t T} is stationary if |r 1| > 1 or |b 1| < 1. 2. If |ri| < 1 or |b 1| > 1 then {xt|t T} exhibits deterministic behaviour. 3. If |ri| = 1 or |b 1| = 1 then {xt|t T} exhibits nonstationary random behaviour.

Special Cases: The AR(2) time Let {xt|t T} be defined by the equation.

Consider the polynomial where r 1 and r 2 are the roots of b(x) 1. {xt|t T} is stationary if |r 1| > 1 and |r 2| > 1. This is true if b 1+b 2 < 1 , b 2 –b 1 < 1 and b 2 > -1. These inequalities define a triangular region for b 1 and b 2. If |ri| < 1 or |b 1| > 1 then {xt|t T} exhibits deterministic behaviour. 3. If |ri| ≥ 1 for i = 1, 2 and |ri| = 1 for at least on i then {xt|t T} exhibits non-stationary random behaviour.

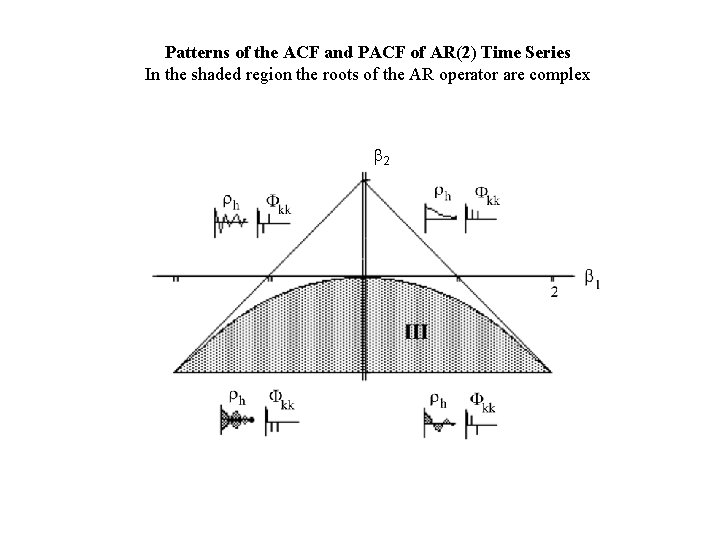
Patterns of the ACF and PACF of AR(2) Time Series In the shaded region the roots of the AR operator are complex b 2

The Mixed Autoregressive Moving Average Time Series of order p, q The ARMA(p, q) series

The Mixed Autoregressive Moving Average Time Series of order p, ARMA(p, q) Let b 1, b 2, … bp , a 1, a 2, … ap , d denote p + q +1 numbers (parameters). Let {ut|t T} denote a white noise time series with variance s 2. – independent – mean 0, variance s 2. Let {xt|t T} be defined by the equation. Then {xt|t T} is called a Mixed Autoregressive. Moving Average time series - ARMA(p, q) series.

Mean value, variance, autocovariance function, autocorrelation function of an ARMA(p, q) series

Similar to an AR(p) time series, for certain values of the parameters b 1, …, bp an ARMA(p, q) time series may not be stationary. An ARMA(p, q) time series is stationary if the roots (r 1, r 2, … , rp ) of the polynomial b(x) = 1 – b 1 x – b 2 x 2 - … - bp xp satisfy | ri| > 1 for all i.

Assume that the ARMA(p, q) time series {xt|t T} is stationary: Let m = E(xt). Then or

The Autocovariance function, s(h), of a stationary mixed autoregressive-moving average time series {xt|t T} be determined by the equation: Thus

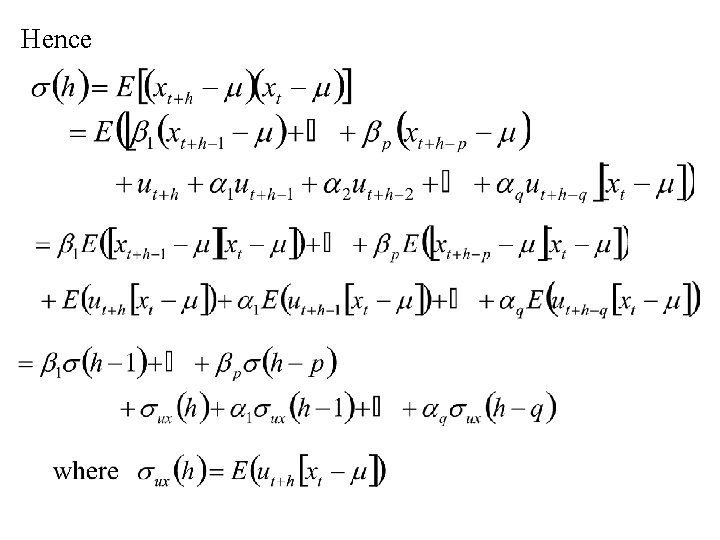
Hence

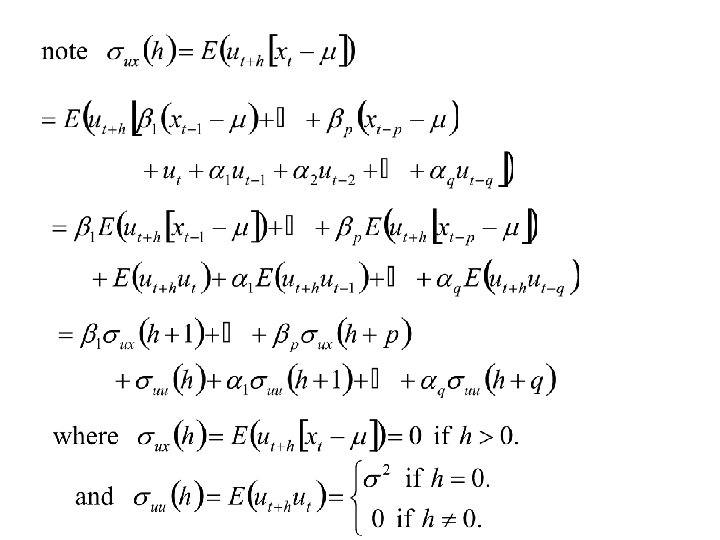
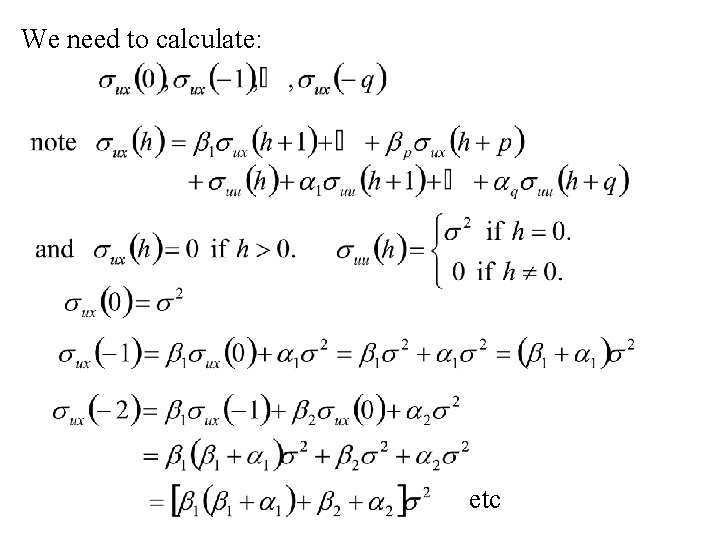
We need to calculate: etc

The autocovariance function s(h) satisfies: For h = 0, 1. … , q: for h > q:

We then use the first (p + 1) equations to determine: s(0), s(1), s(2), … , s(p) We use the subsequent equations to determine: s(h) for h > p.

Example: The autocovariance function, s(h), for an ARMA(1, 1) time series: For h = 0, 1: or for h > 1:

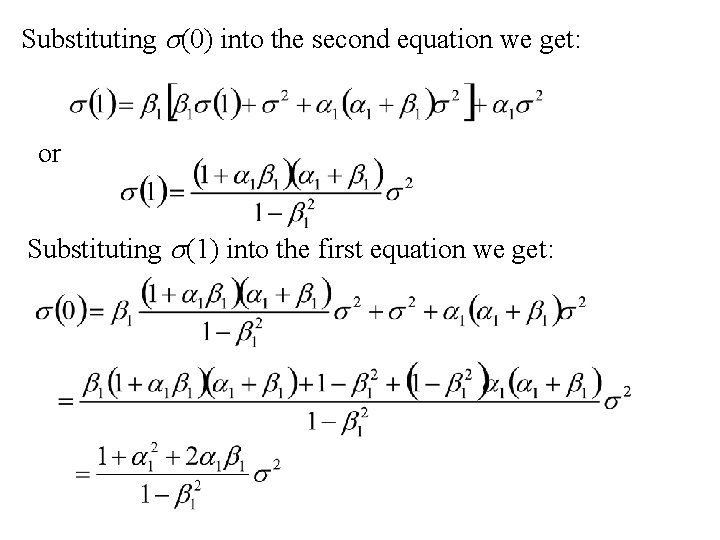
Substituting s(0) into the second equation we get: or Substituting s(1) into the first equation we get:

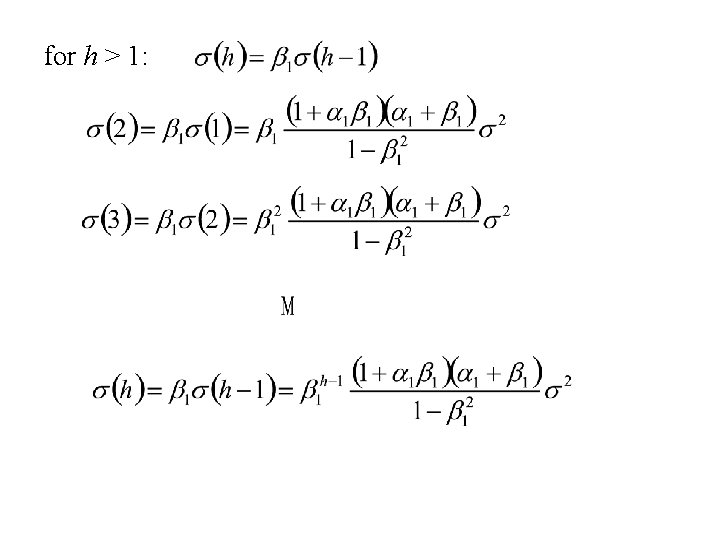
for h > 1:

The Backshift Operator B

Consider the time series {xt : t T} and Let M denote the linear space spanned by the set of random variables {xt : t T} (i. e. all linear combinations of elements of {xt : t T} and their limits in mean square). M is a vector space Let B be an operator on M defined by: Bxt = xt-1. B is called the backshift operator.

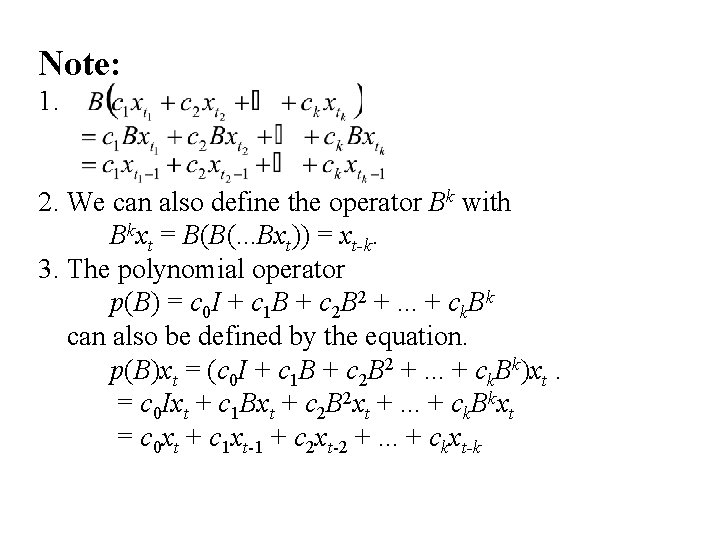
Note: 1. 2. We can also define the operator Bk with Bkxt = B(B(. . . Bxt)) = xt-k. 3. The polynomial operator p(B) = c 0 I + c 1 B + c 2 B 2 +. . . + ck. Bk can also be defined by the equation. p(B)xt = (c 0 I + c 1 B + c 2 B 2 +. . . + ck. Bk)xt. = c 0 Ixt + c 1 Bxt + c 2 B 2 xt +. . . + ck. Bkxt = c 0 xt + c 1 xt-1 + c 2 xt-2 +. . . + ckxt-k

4. The power series operator p(B) = c 0 I + c 1 B + c 2 B 2 +. . . can also be defined by the equation. p(B)xt = (c 0 I + c 1 B + c 2 B 2 +. . . )xt = c 0 Ixt + c 1 Bxt + c 2 B 2 xt +. . . = c 0 xt + c 1 xt-1 + c 2 xt-2 +. . . 5. If p(B) = c 0 I + c 1 B + c 2 B 2 +. . . and q(B) = b 0 I + b 1 B + b 2 B 2 +. . . are such that p(B)q(B) = I i. e. p(B)q(B)xt = Ixt = xt than q(B) is denoted by [p(B)]-1.

Other operators closely related to B: 1. F = B-1 , the forward shift operator, defined by Fxt = B-1 xt = xt+1 and 2. D = I - B , the first difference operator, defined by Dxt = (I - B)xt = xt - xt-1.

The Equation for a MA(q) time series xt= a 0 ut + a 1 ut-1 +a 2 ut-2 +. . . +aqut-q + m can be written xt= a(B) ut + m where a(B) = a 0 I + a 1 B +a 2 B 2 +. . . +aq. Bq

The Equation for a AR(p) time series xt= b 1 xt-1 +b 2 xt-2 +. . . +bpxt-p + d + ut can be written b(B) xt= d + ut where b(B) = I - b 1 B - b 2 B 2 -. . . - bp. Bp

The Equation for a ARMA(p, q) time series xt= b 1 xt-1 +b 2 xt-2 +. . . +bpxt-p + d + ut + a 1 ut-1 +a 2 ut-2 +. . . +aqut-q can be written b(B) xt= a(B) ut + m where a(B) = a 0 I + a 1 B +a 2 B 2 +. . . +aq. Bq and b(B) = I - b 1 B - b 2 B 2 -. . . - bp. Bp

Some comments about the Backshift operator B 1. It is a useful notational device, allowing us to write the equations for MA(q), AR(p) and ARMA(p, q) in a very compact form; 2. It is also useful for making certain computations related to the time series described above;

The partial autocorrelation function A useful tool in time series analysis

The partial autocorrelation function Recall that the autocorrelation function of an AR(p) process satisfies the equation: rx(h) = b 1 rx(h-1) + b 2 rx(h-2) +. . . +bprx(h-p) For 1 ≤ h ≤ p these equations (Yule-Walker) become: rx(1) = b 1 + b 2 rx(1) +. . . +bprx(p-1) rx(2) = b 1 rx(1) + b 2 +. . . +bprx(p-2). . . rx(p) = b 1 rx(p-1)+ b 2 rx(p-2) +. . . +bp.

In matrix notation: These equations can be used to find b 1, b 2, … , bp, if the time series is known to be AR(p) and the autocorrelation rx(h)function is known.

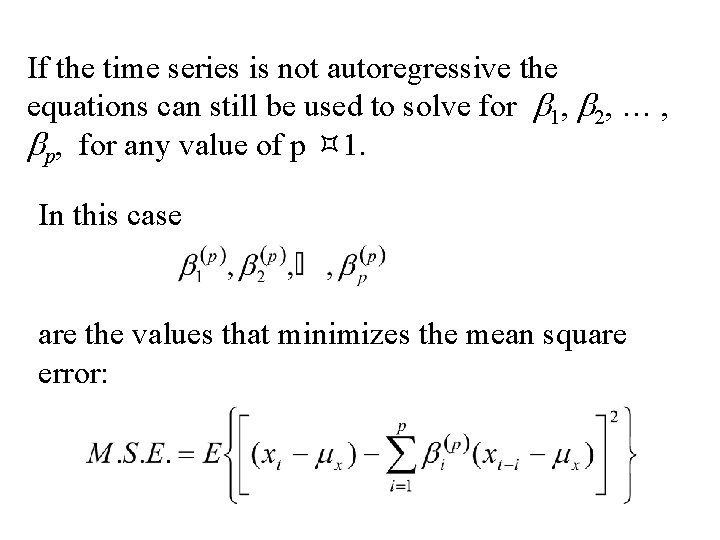
If the time series is not autoregressive the equations can still be used to solve for b 1, b 2, … , bp, for any value of p 1. In this case are the values that minimizes the mean square error:

Definition: The partial auto correlation function at lag k is defined to be:

Comment: The partial auto correlation function, Fkk is determined from the auto correlation function, r(h)

Some more comments: 1. The partial autocorrelation function at lag k, Fkk, can be interpreted as a corrected autocorrelation between xt and xt-k conditioning on the intervening variables xt-1, xt-2, . . . , xt-k+1. 2. If the time series is an AR(p) time series than Fkk = 0 for k > p 3. If the time series is an MA(q) time series than rx(h) = 0 for h > q

A General Recursive Formula for Autoregressive Parameters and the Partial Autocorrelation function (PACF)

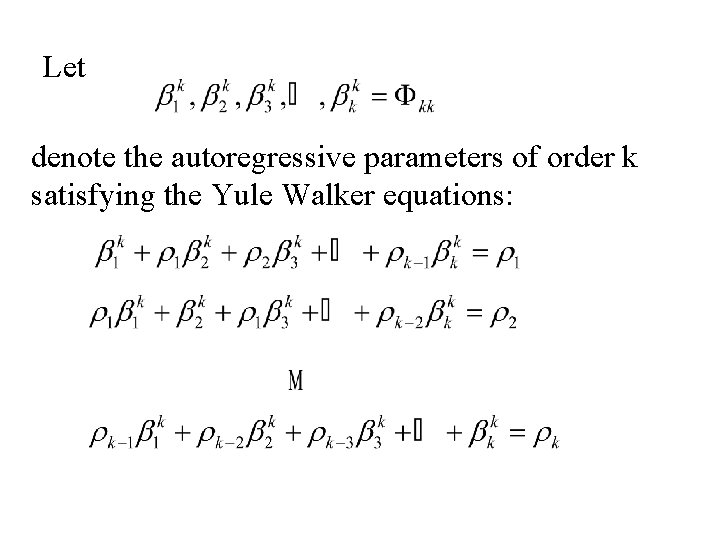
Let denote the autoregressive parameters of order k satisfying the Yule Walker equations:

Then it can be shown that: and

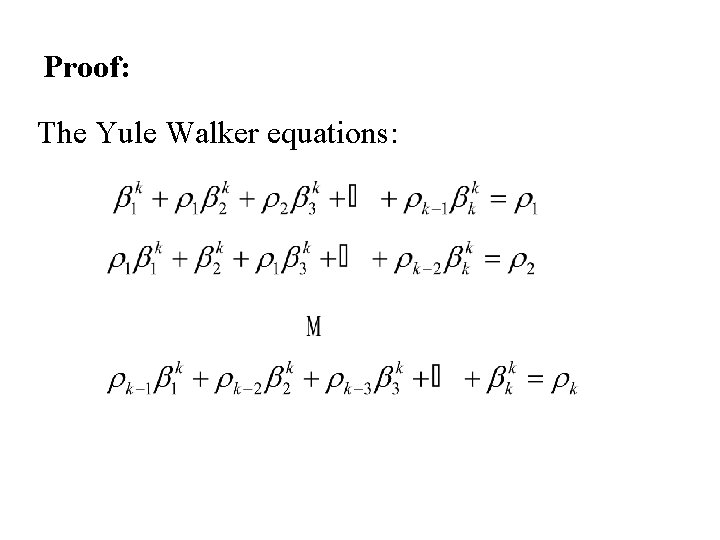
Proof: The Yule Walker equations:

In matrix form:

The equations for

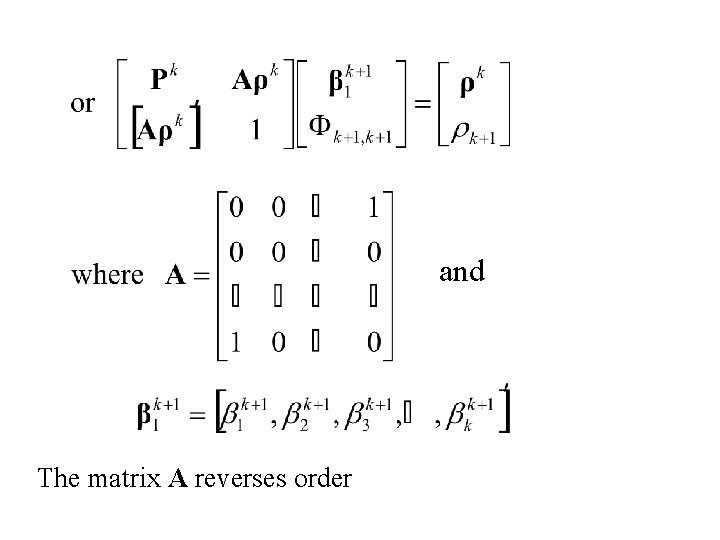
and The matrix A reverses order

The equations may be written Multiplying the first equations by or

Substituting this into the second equation or and

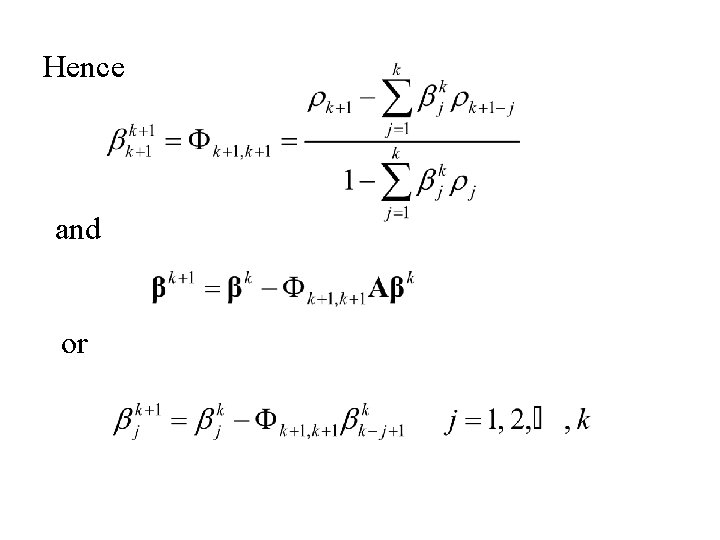
Hence and or

Some Examples

Example 1: MA(1) time series Suppose that {xt|t T} satisfies the following equation: xt = 12. 0 + ut + 0. 5 ut – 1 where {ut|t T} is white noise with s = 1. 1. Find: 1. The mean of the series, 2. The variance of the series, 3. The autocorrelation function. 4. The partial autocorrelation function.

Solution Now {xt|t T} satisfies the following equation: xt = 12. 0 + ut + 0. 5 ut – 1 Thus: 1. The mean of the series, m = 12. 0 The autocovariance function for an MA(1) is

Thus: 2. The variance of the series, s(0) = 1. 5125 and 3. The autocorrelation function is:

4. The partial auto correlation function at lag k is defined to be: Thus

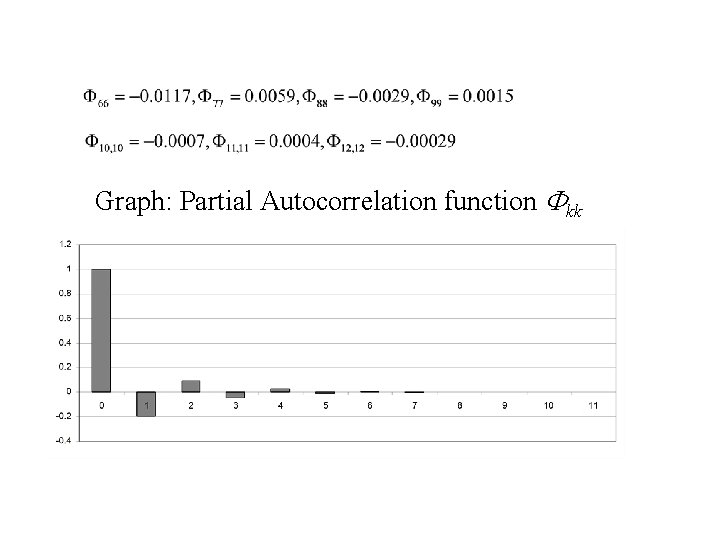
Graph: Partial Autocorrelation function Fkk

Exercise: Use the recursive method to calculate Fkk and

Exercise: Use the recursive method to calculate Fkk and

Example 2: AR(2) time series Suppose that {xt|t T} satisfies the following equation: xt = 0. 4 xt – 1 + 0. 1 xt – 2 + 1. 2 + ut where {ut|t T} is white noise with s = 2. 1. Is the time series stationary? Find: 1. The mean of the series, 2. The variance of the series, 3. The autocorrelation function. 4. The partial autocorrelation function.

1. The mean of the series 3. The autocorrelation function. Satisfies the Yule Walker equations

hence

2. the variance of the series 4. The partial autocorrelation function.

The partial autocorrelation function of an AR(p) time series “cuts off” after p.

Example 3: ARMA(1, 2) time series Suppose that {xt|t T} satisfies the following equation: xt = 0. 4 xt – 1 + 3. 2 + ut + 0. 3 ut – 1 + 0. 2 ut – 1 where {ut|t T} is white noise with s = 1. 6. Is the time series stationary? Find: 1. The mean of the series, 2. The variance of the series, 3. The autocorrelation function. 4. The partial autocorrelation function.