Datastrukturer och algoritmer Frelsning 6 Fr kort kan

Datastrukturer och algoritmer Föreläsning 6 För kort, kan ökas en kvart. . .

Datastrukturer och algoritmer Innehåll 2 u Asymptotisk u Kapitel komplexitetsanalys 12. 1 -12. 4 forts.

Datastrukturer och algoritmer Repetition: Experimentell analys 3 u Implementera algoritmen Ø Kör programmet med varierande datamängd o o Storlek Sammansättning Ø Använd metoder för tidtagning Ø Plotta uppmätt data u Begränsningar med metoden Ø Måste implementera och testa algoritmen Ø Svårt att veta om programmet har stannat eller fast i beräkningarna. T ex. 2 n; n=100 => 40000 billioner år Ø Experimenten kan endast utföras på en begränsad mängd av data, man kan missa viktiga testdata Ø Hårdvaran och mjukvaran måste vara den samma för alla implementationer

Datastrukturer och algoritmer Sökes: Generellare metod som. . . 4 u. . . använder en högnivåbeskrivning av algoritmerna istället för en implementation av den u. . . tar hänsyn till alla möjliga indata u. . . analyserar oberoende av hårdvaran och mjukvaran

Datastrukturer och algoritmer Asymptotisk analys 5 u Utgå från pseudokoden u Räkna primitiva operationer Ø Ställ upp ett tidsuttryck T(n) för antalet operationer beroende av problemstorleken Ø Tmax(n) men också Tmedel(n) och Tmin(n) kan vara intressant. u Förenkla tidsuttrycket u Ta fram en funktion som begränsar tidsuttrycket ovanifrån…

Datastrukturer och algoritmer Primitiva operationer Lågnivåberäkningar som är i stort sett oberoende av programspråk och kan definieras i termer av pseudokod. u Beslutar att alla primitiva operationer kostar 1 tidssteg. u Grov förenkling! I verkligheten tar operationerna olika lång tid! u Ø Vi får en maskinoberoende analys, en analys som gäller på alla maskiner nu och i framtiden. u Alternativet är att titta på de verkliga tiderna för de olika operationerna Ø Ger en maskinberoende analys 6

Datastrukturer och algoritmer Primitiva operationer 7 u Följande antas kosta ett (1) tidssteg: Ø Anropa en metod/funktion Ø Returnera från en metod/funktion Ø Utföra en aritmetisk operation (+, -, …) Ø Utföra en relationsoperation (<, >, <=, . . ) Ø Referera till en variabel eller ett objekt Ø Indexera i en array

Datastrukturer och algoritmer Exempel 8 Hur ser det värsta och det bästa fallet ut för denna algoritm? 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A 4. current. Max 5. for i A[0] 1 to n-1 do 6. if current. Max < A[i] then 7. current. Max A[i] 8. return current. Max Värsta fallet: If-satsen sann för varje varv i loopen. Listan sorterad stigande. Bästa fallet: If-satsen falsk för varje varv i loopen. Max elem först i listan.

Datastrukturer och algoritmer Exempel 9 1 -3: kostar inget 4: indexering i array + tilldelning 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A 4. current. Max A[0] // 1 + 1 5. for i 1 to n-1 do 6. if current. Max < A[i] then 7. current. Max A[i] 8. return current. Max

Datastrukturer och algoritmer Exempel 10 5: En for-loop består av initialisering, kontroll av loopvillkor och själva loopen. 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A Init: beräkna n-1 och lagra undan det, i 1 Loopkoll: görs alltid en gång mer än loopen! I loopen ökas i med 1 4. current. Max A[0] // 1 + 1 5. for i 1 to n-1 do // 1+1+1+1 + n(1+1+1) + (n-1)([] + 1+1+1) 6. if current. Max < A[i] then 7. current. Max A[i] 8. return current. Max

Datastrukturer och algoritmer Exempel 11 6: If-satsen: indexering i array, två variabelreferenser, jämförelse 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A 4. current. Max A[0] // 1 + 1 5. for i 1 to n-1 do // 1+1+1+1 + n(1+1+1) + (n-1)([] + 1+1+1) 6. if current. Max < A[i] then // 1+1+1+1 7. current. Max A[i] 8. return current. Max

Datastrukturer och algoritmer Exempel 12 7: indexering i array, variabelreferens, tilldelning 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A 4. current. Max A[0] // 1 + 1 5. for i 1 to n-1 do // 1+1+1+1 + n(1+1+1) + (n-1)([] + 1+1+1) 6. if current. Max < A[i] then // 1+1+1+1 7. current. Max A[i] // 1+1+1 8. return current. Max

Datastrukturer och algoritmer Exempel 13 8: variabelreferens, returnering 1. Algorithm array. Max(A, n) 2. input: An array A storing n integers 3. output: The maximum element in A 4. current. Max A[0] // 1 + 1 5. for i 1 to n-1 do // 1+1+1+1 + n(1+1+1) + (n-1)([] + 1+1+1) 6. if current. Max < A[i] then // 1+1+1+1 7. current. Max A[i] // 1+1+1 8. return current. Max // 1+1

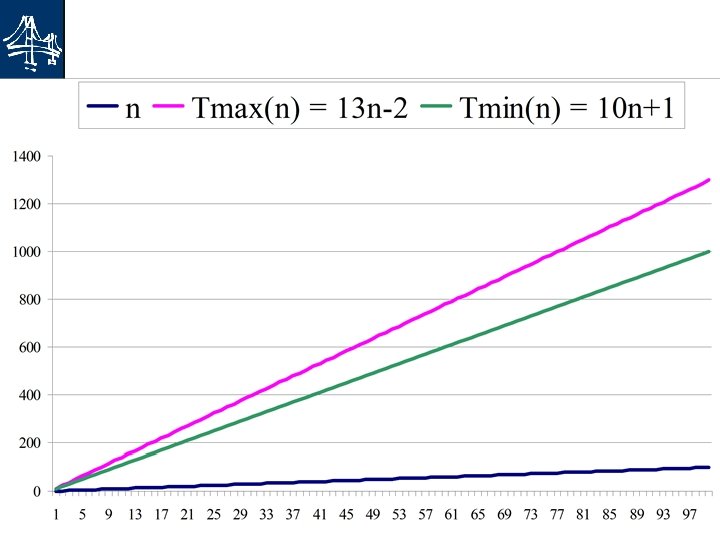
Datastrukturer och algoritmer Vilka tidsfunktioner får vi då? 14 u Värsta fallet: if-satsen alltid sann Ø Tmax(n)= 2+4+3 n+10(n-1)+2 = 8+3 n+10 n-10 = 13 n-2 u Bästa fallet: if-satsen alltid falsk Ø Tmax(n)= 2+4+3 n+7(n-1)+2 = 8+3 n+7 n-7 = 10 n+1

15 Datastrukturer och algoritmer

Datastrukturer och algoritmer Jämföra T(n) 16 u Förenkla jämförelsen genom att avrunda T(n) Ø 1. 000001 ≈ 1 Ø 3 n 2 ≈ n 2

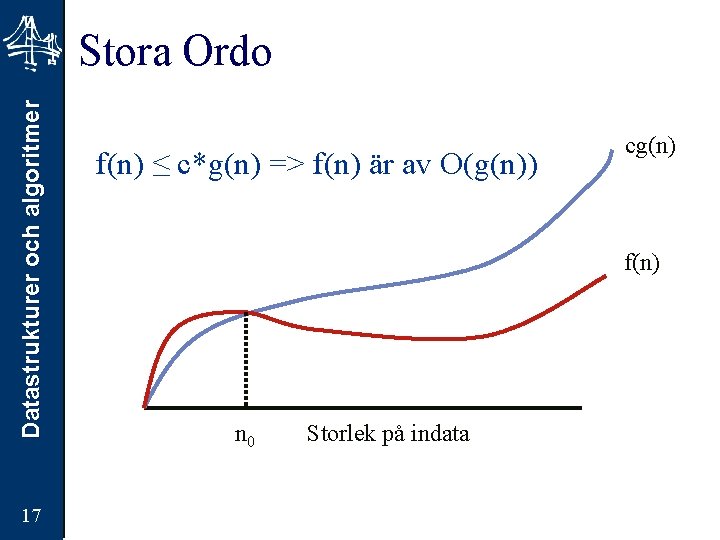
Datastrukturer och algoritmer Stora Ordo 17 f(n) ≤ c*g(n) => f(n) är av O(g(n)) cg(n) f(n) n 0 Storlek på indata

Datastrukturer och algoritmer Definition 18 Definition: Givet funktionerna f(n) och g(n) säger vi att f(n) är O(g(n)) om och endast om f(n) ≤ c*g(n) för n ≥ n 0 och c > 0 och n 0 ≥ 1

Datastrukturer och algoritmer f(n) är O(g(n)) 19 u O(g(n)) är en mängd av funktioner som alla har egenskapen definitionen handlar om. u De är uppenbarligen oändligt många – så vi är intresserad av den ”minsta”. Ø Bortse från allt utom den snabbast växande termen i funktionen. Ø Ta bort konstanta faktorer.

Datastrukturer och algoritmer Förenklingar 20 7 n-3 är O(n) u 10 n 2 + 3 n 5 + 10000 är O(n 5) u 7 n 3 + 50 n 2 + 4 log(n) är O(n 3) u 8 n 2 log(n) + 5 n 2 + n är O(n 2 log(n)) u u Men vi måste ju ta hänsyn till konstanterna c och n 0 också!

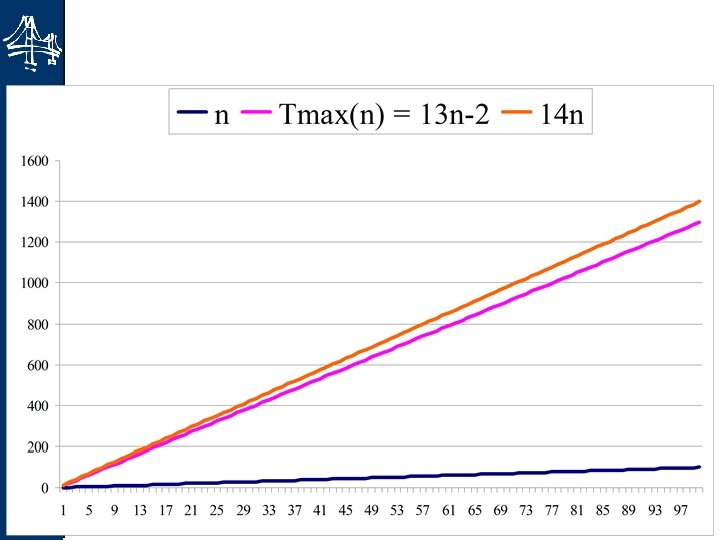
Datastrukturer och algoritmer c och n 0 21 Tmax(n) = 13 n − 2 är O(n) om vi kan finna rätt värden på c och n 0. u Generellt räknar man ut c på följande sätt: u u I vårt fall får vi då: u Sen måste vi beräkna n 0 också. 13 n – 2 14 n n 0 = 1 uppfyller detta!

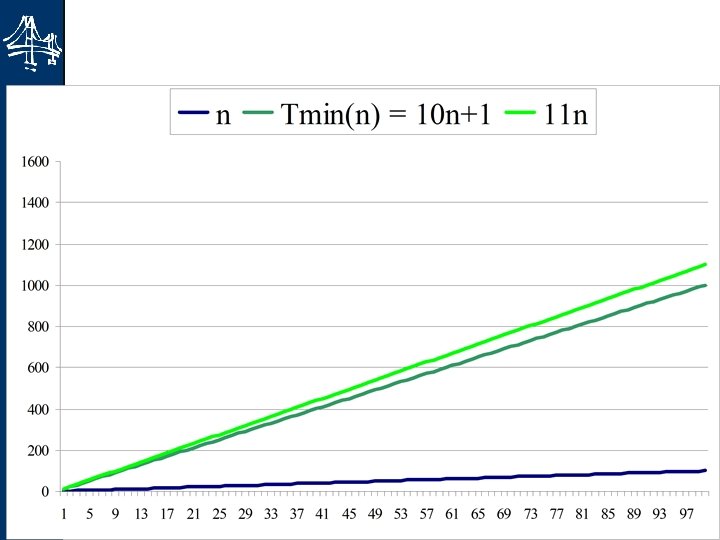
Datastrukturer och algoritmer c och n 0 i det bästa fallet då? 22 Tmax(n) = 10 n + 1 är O(n) om vi kan finna rätt värden på c och n 0. u Vi får: u u Sen måste vi beräkna n 0 också. 10 n + 1 11 n n 0 = 1 uppfyller detta!

23 Datastrukturer och algoritmer

24 Datastrukturer och algoritmer

Datastrukturer och algoritmer Specialla klasser av algoritmer 25 u Logaritmiska u Linjära u Kvadradiska u Polynoma u Exponentiella u log(n) O(log(n)) O(n 2) O(nk); k ≥ 1 O(an); n ≥ 1 <<n<<n 2<<n 3<<2 n

Datastrukturer och algoritmer Sammanfattning 26 u O(n) används för att utrycka antalet primitiva operationer som utförs som en funktion av storleken på indata u En övre gräns för tillväxt u array. Max är en linjär algoritm dvs O(n) u En algoritm som körs på O(n) är bättre än en O(n 2), men O(log(n)) är bättre än O(n)

Datastrukturer och algoritmer Varning 27 u Var aktsam, stora konstanter ställer till det Ø T(n)=1000000 n är en linjär algoritm O(n), men i många fall mycket mindre effektiv på data mängder än en algoritm med T(n) = 2 n 2 som är O(n 2) Ø O-notationen är en stor förenkling, dvs en övre gräns, det finns släktingar som begränsar nedåt.

Datastrukturer och algoritmer Genväg 28 u Man kan strunta i att beräkna T(n) Ø Väldigt grov uppskattning av tillväxten Ø Man gör en okulärbesiktning av algoritmen o Initiera en array är O(n) o Nästlade loopar är O(n)*…*O(n)≈O(nk)

Datastrukturer och algoritmer Exempel 1 29 Algorithm prefix. Av 1(X); Input: An n-element Array of numbers Output: An n-element Array of numbers such that A[i] is the average of X[0], …, X[i]. Let A be an array of numbers for i 0 to n-1 do a 0 for j 0 to i do a a+X[j] A[i] a/(i+1) return A Analys: Tb(n) = ? Tw(n) = ? Men algoritmen är av O(n 2)

Datastrukturer och algoritmer Exempel 2 30 Algorithm prefix. Av 1(X); Input: An n-element Array of numbers Output: An n-element Array of numbers such that A[i] is the average of X[0], …, X[i]. Let A be s 0 for i s A[i] return A an array of numbers 0 to n-1 do s+X[i] s/(i+1) Analys: T(n) = ? Men algoritmen är av O(n)

Datastrukturer och algoritmer Matematikrepetition 31 u Logaritmer Ø Ø u logb(xy) = logb(x) + logb(y) logb(x/y) = logb(x) - logb(y) logb(x ) = logb(x) logb(a) =loga(x)/loga(b) Exponenter Ø Ø Ø

Datastrukturer och algoritmer Summor och serier 32 u Generell definition u Geometrisk utveckling (n≥ 0 och 0<a ≠ 1) Ø Växer exponentiellt u Aritmetisk tillväxt, summera alla tal från 1 tomn