Datamining Methods Mining Association Rules and Sequential Patterns

Datamining Methods Mining Association Rules and Sequential Patterns P. Brezany Institut für Scientific Computing - Universität Wien

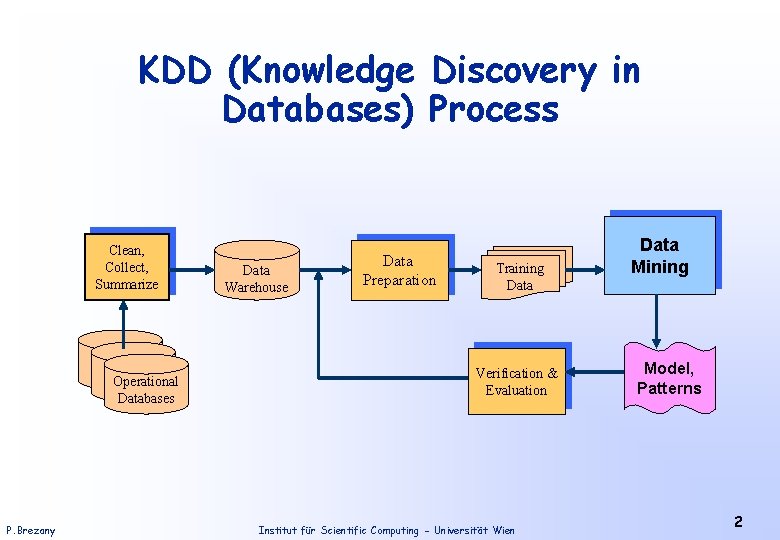
KDD (Knowledge Discovery in Databases) Process Clean, Collect, Summarize Operational Databases P. Brezany Data Warehouse Data Preparation Training Data Verification & Evaluation Institut für Scientific Computing - Universität Wien Data Mining Model, Patterns 2

Mining Association Rules • Association rule mining finds interesting association or correlationships among a large set of data items. • This can help in many business decision making processes: store layout, catalog design, and customer segmentation based on buying paterns. Another important field: medical applications. • Market basket analysis - a typical example of association rule mining. • How can we find association rules from large amounts of data? Which association rules are the most interesting. How can we help or guide the mining procedures? P. Brezany Institut für Scientific Computing - Universität Wien 3

Informal Introduction • Given a set of database transactions, where each transaction is a set of items, an association rule is an expression X Y where X and Y are sets of items (literals). The intuitive meaning of the rule: transactions in the database which contain the items in X tend to also contain the items in Y. • Example: 98% of customers who purchase tires and auto accessories also buy some automotive services; here 98% is called the confidence of the rule. The support of the rule is the percentage of transactions that contain both X and Y. • The problem of mining association rules is to find all rules that satisfy a user-specified minimum support and minimum confidence. P. Brezany Institut für Scientific Computing - Universität Wien 4

Basic Concepts Let J = (i 1, i 2, . . . , im) be a set of items. Typically, the items are identifiers of individuals articles (products (e. g. , bar codes). Let D, the task relevant data, be a set of database transactions where each transaction T is a set of items such that T J. Let A be a set of items: a transaction T is said to contain A if and only if A T, An association rule is an implication of the form A B, where A J, B J, and A B = . The rule A B holds in the transaction set D with support s, where s is the percentage of transactions in D that contain A B (i. e. both A and B). This is the probability, P(A B). P. Brezany Institut für Scientific Computing - Universität Wien 5

Basic Concepts (Cont. ) The rule A B has confidence c in the transaction set D if c is the percentage of transactions in D containing A that also contain B - the conditional probability P(B|A). Rules that satisfy both a minimum support threshold (min_sup) and a minimum confidence threshold (min_conf) are called strong. A set of items is referred to as an itemset. An itemset that contains k items is a k-itemset. The occurence frequency of an itemset is the number of transactions that contain the itemset. P. Brezany Institut für Scientific Computing - Universität Wien 6

Basic Concepts - Example transaction 1 2 3 4 5 6 purchased items bread, coffee, milk, cake bread, butter, coffee, milk, cake bread X = {coffee, milk} R = {coffee, cake, milk} support of X = 3 from 6 = 50% support of R = 2 from 6 = 33% Support of “milk, coffee” “cake” equals to support of R = 33% Confidence of “milk, coffee” “cake” = 2 from 3 = 67% [=support(R)/support(X)] P. Brezany Institut für Scientific Computing - Universität Wien 7

Basic Concepts (Cont. ) An itemset satisfies minimum support if the occurrence frequency of the itemset is greater than or equal to the product of min_sup and the total number of transactions in D. The number of transactions required for the itemset to satisfy minimum support is therefore referred to as the minimum support count. If an itemset satisfy minimum support, then it is a frequent itemset. The set of frequent k-itemsets is commonly denoted by Lk. Association rule mining is a two-step process: 1. Find all frequent itemsets. 2. Generate strong association rules from the frequent itemsets. P. Brezany Institut für Scientific Computing - Universität Wien 8

Association Rule Classification • Based on the types of values handled in the rule: If a rule concerns associations between the presence or absence of items, it is a Boolean association rule. For example: computer financial_management_software [support = 2%, confidence = 60%] If a rule describes associations between quantitative items or attributes, then it is a quantitative association rule. For example: age(X, “ 30. . 39”) and income(X, ” 42 K. . 48 K”) buys(X, high resolution TV) Note that the quantitative attributes, age and income, have been discretized. P. Brezany Institut für Scientific Computing - Universität Wien 9

Association Rule Classification (Cont. ) • Based on the dimensions of data involved in the rule: If the items or attributes in an association rule reference only one dimension, then it is a single dimensional association rule. For example: buys(X, ”computer”) buys (X, “financial management software”) The above rule refers to only one dimension, buys. If a rule references two or more dimensions, such as buys, time_of_transaction, and customer_category, then it is a multidimensional association rule. The second rule on the previous slide is a 3 -dimensional ass. rule since it involves 3 dimensions: age, income, and buys. P. Brezany Institut für Scientific Computing - Universität Wien 10

Association Rule Classification (Cont. ) • Based on the levels of abstractions involved in the rule set: Suppose that a set of association rules minded includes: age(X, ” 30. . 39”) buys(X, “laptop computer”) age(X, ” 30. . 39”) buys(X, “computer”) In the above rules, the items bought are referenced at different levels of abstraction. (E. g. , “computer” is a higher-level abstraction of “laptop computer”. ) Such rules are called multilevel association rules. Single-level association rules refer one abstraction level only. P. Brezany Institut für Scientific Computing - Universität Wien 11

Mining Single-Dimensional Boolean Association Rules from Transactional Databases This is the simplest form of association rules (used in market basket analysis. We present Apriori, a basic algorithm for finding frequent itemsets. Its name – it uses prior knowledge of frequent itemset properties (explained later). Apriori employs a iterative approach known as a level-wise search, where k-itemsets are used to explore (k + 1)-itemsets. First, the set of frequent 1 -items, L 1, is found. L 1 is used to find L 2, the set of frequent 2 -itemsets, which is used to find L 3, and so on, until no more frequent k-itemsets can be found. The finding of each Lk requires one full scan of the database. The Apriori property is used to reduce the search space. P. Brezany Institut für Scientific Computing - Universität Wien 12

The Apriori Property All nonempty subsets of a frequent itemset must also be frequent. If an itemset I does not satisfy the minimum support threshold, min_sup, then I is not frequent, that is, P(I) < min_sup. If an item A is added to the itemset I, then the resulting itemset (i. e. , I A ) cannot occur more frequently than I. Therefore, I A is not frequent either, that is, P (I A ) < min_sup. How is the Apriori property used in the algorithm? To understand this, let us look at how Lk-1 is used to find Lk. A two-step process is followed, consisting of join and prune actions. These steps are explained on the next slides, P. Brezany Institut für Scientific Computing - Universität Wien 13

The Apriori Algorithm – the Join Step To find Lk, a set of candidate k-itemsets is generated by joining Lk-1 with itself. This set of candidates is denoted by Ck. Let l 1 and l 2 be itemsets in Lk-1. The notation li[j] refers to the jth item in li (e. g. , li[k-2] refers to the second to the last item in l 1). Apriori assumes that items within a transaction or itemset are sorted in lexicographic order. The join Lk-1, is performed, where members of Lk-1 are joinable if their first (k-2) items are in common. That is, members l 1 and l 2 of Lk-1 are joined if (l 1[1] = l 2[1] ) (l 1[2] = l 2[2] ) . . . (l 1[k-2] = l 2[k-2] ) (l 1[k-1] < l 2[k-1] ). The condition (l 1[k-1] < l 2[k-1] ) simply ensures that no duplicates are generated. The resulting itemset: l 1[1] l 1[2] ). . . l 1[k-1] l 2[k-1]. P. Brezany Institut für Scientific Computing - Universität Wien 14

The Apriori Algorithm – the Join Step (2) Illustration by an example p Lk-1 = ( 1 2 3) || || Join: Result Ck = ( 1 2 3 4) || || q Lk-1 = ( 1 2 4) Each frequent k-itemset p is always extended by the last item of all frequent itemsets q which have the same first k-1 items as p. P. Brezany Institut für Scientific Computing - Universität Wien 15

The Apriori Algorithm – the Prune Step Ck is a superset of Lk, that is, its members may or may not be frequent, but all of the frequent k-items are included in C k. A scan of the database to determine the count of each candidate in Ck would result in the determination of Lk. Ck can be huge, and so this could involve heavy computation. To reduce the size of Ck, the Apriori property is used as follows. Any (k-1)-itemset that is not frequent cannot be a subset of a frequent k-itemset. Hence, if any (k-1)-subset of a candidate k-itemset is not in Lk-1, then the candidate cannot be frequent either and so can be removed from Ck. The above subset testing can be done quickly by maintaining a hash tree of all frequent itemsets. P. Brezany Institut für Scientific Computing - Universität Wien 16

The Apriori Algorithm - Example Let’s look at a concrete example of Apriori, based on the All. Electronics transaction database D, shown below. There are nine transactions in this database, e. i. , |D| = 9. We use the next figure to illustrate the fin. TID List of item_Ids ding of frequent itemsets T 100 I 1, I 2, I 5 in D. T 200 I 2, I 4 P. Brezany T 300 T 400 T 500 T 600 T 700 T 800 T 900 I 2, I 3 I 1, I 2, I 4 I 1, I 3 I 2, I 3 I 1, I 2, I 3, I 5 I 1, I 2, I 3 Institut für Scientific Computing - Universität Wien 17

Generation of CK and LK (min. supp. count=2) Scan D for count of each candidate- scan Itemset Sup. count {I 1} 6 {I 2} 7 {I 3} 6 {I 4} 2 {I 5} 2 Compare candidate support count with minimum support count - compare C 1 Generate C 2 candidates from L 1 Itemset {I 1, I 2} {I 1, I 3} {I 1, I 4} {I 1, I 5} {I 2, I 3} {I 2, I 4} {I 2, I 5} {I 3, I 4} {I 3, I 5} {I 4, I 5} C 2 P. Brezany Scan Itemset Sup. count {I 1} 6 {I 2} 7 {I 3} 6 {I 4} 2 {I 5} 2 L 1 Itemset Sup. count {I 1, I 2} 4 {I 1, I 3} 4 {I 1, I 4} 1 {I 1, I 5} 2 {I 2, I 3} 4 {I 2, I 4} 2 {I 2, I 5} 2 {I 3, I 4} 0 {I 3, I 5} 1 {I 4, I 5} 0 C 2 Itemset Sup. count {I 1, I 2} 4 4 Compare {I 1, I 3} {I 1, I 5} 2 {I 2, I 3} 4 {I 2, I 4} 2 {I 2, I 5} 2 Institut für Scientific Computing - Universität Wien L 2 18

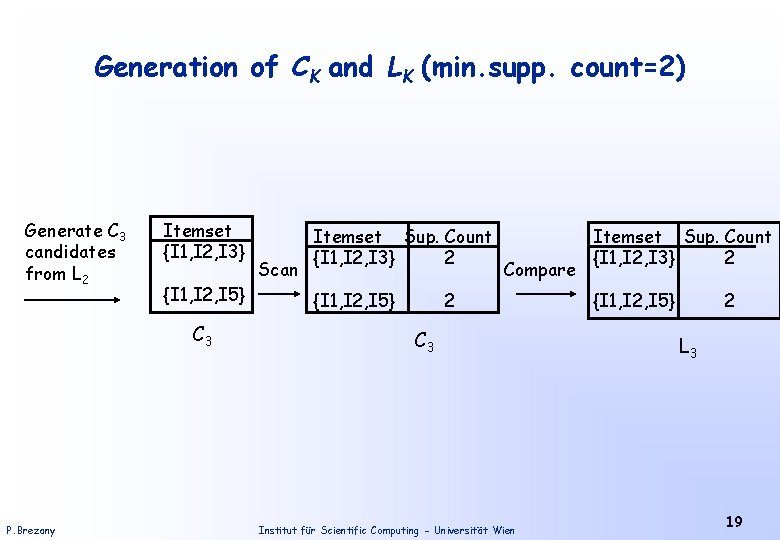
Generation of CK and LK (min. supp. count=2) Generate C 3 candidates from L 2 Itemset {I 1, I 2, I 3} {I 1, I 2, I 5} C 3 P. Brezany Scan Itemset Sup. Count {I 1, I 2, I 3} 2 {I 1, I 2, I 5} Compare 2 C 3 Institut für Scientific Computing - Universität Wien Itemset Sup. Count {I 1, I 2, I 3} 2 {I 1, I 2, I 5} 2 L 3 19

Algorithm Application Description 1 In the 1 st iteration, each item is a member of C 1. The algorithm simply scan all the transactions in order to count the number of occurrences of each item. 2 Suppose that the minimum transaction support count (min_sup = 2/9 = 22%). L 1 can then be determined. 3 C 2 = L 1 join L 1. 4 The transactions in D are scanned and the support count of each candidate itemset in C 2 , as shown in the middle table of the second row in the last figure. 5 The set of frequent 2 -itemsets, L 2 , is then determined, consisting of those candidate 2 -itemsets in C 2 having minimum support. P. Brezany Institut für Scientific Computing - Universität Wien 20

Algorithm Application Description (2) 6 The generation of C 3 = L 2 join L 2 is detailed in the next figure. Based on the Apriori property that all subsets of a frequent itemset must also be frequent, we can determine that the four latter candidates cannot possibly be frequent. We therefore remove them from C 3. 7 The transactions in D are scanned in order to determine L 3 , consisting of those candidate 3 -itemsets in C 3 having minimum support. 8 C 4 = L 3 join L 3 , after the pruning C 4 = Ø. P. Brezany Institut für Scientific Computing - Universität Wien 21

Example: Generation C 3 from L 2 1. Join: C 3 = L 2 = {{I 1, I 2}, {I 1, I 3}, {I 1, I 5}, {I 2, I 3}, {I 2, I 4}, {I 2, I 5}} = {{I 1, I 2, I 3}, {I 1, I 2, I 5}, {I 1, I 3, I 5}, {I 2, I 3, I 4}, {I 2, I 3, I 5}, {I 2, I 4, I 5}}. 2. Prune using the Apriori property: All nonempty subsets of a frequent itemset must also be frequent. The 2 -item subsets of {I 1, I 2, I 3} are {I 1, I 2}, {I 1, I 3}, {I 2, I 3}, and they all are members of L 2. Therefore, keep {I 1, I 2, I 3} in C 3. The 2 -item subsets of {I 1, I 2, I 5} are {I 1, I 2}, {I 1, I 5}, {I 2, I 5}, and they all are members of L 2. Therefore, keep {I 1, I 2, I 5} in C 3. Using the same analysis remove other 3 -items from C 3. 3. Therefore, C 3 = {{I 1, I 2, I 3}, {I 1, I 2, I 5}} after pruning. P. Brezany Institut für Scientific Computing - Universität Wien 22

Generating Association Rules from Frequent Items We generate strong association rules - they satisfy both minimum support and minimum confidence. support_count(A B) confidence ( A B ) = P(B|A) = ------------support_count(A) where support_count(A B) is the number of transactions containing the itemsets A B, and support_count(A) is the number of transactions containing the itemset A. P. Brezany Institut für Scientific Computing - Universität Wien 23

Generating Association Rules from Frequent Items (Cont. ) Based on the equations on the previous slide, association rules can be generated as follows: - For each frequent itemset l , generate all nonempty subsets of l. - For every nonempty subset s of l, output the rule “s (l - s)” support_count(l) if --------- min_conf, where min_conf is minimum support_count(s) confidence threshold. P. Brezany Institut für Scientific Computing - Universität Wien 24

Generating Association Rules - Example Suppose that the transactional data for All. Electronics contain the frequent itemset l = {I 1, I 2, I 5}. The resulting rules are: I 1 I 2 I 5 I 5 I 2 I 1 I 5, I 2, I 1, I 5, I 2, confidence = 2/4 = 50% confidence = 2/2 = 100% confidence = 2/6 = 33% confidence = 2/7 = 29% confidence = 2/2 = 100% If the minimum confidence threshold is, say, 70%, then only the second, third, and the last rules above are output, since these are the only ones generated that are strong. P. Brezany Institut für Scientific Computing - Universität Wien 25

Multilevel (Generalized) Association Rules For many applications, it is difficult to find strong associations among data items at low or primitive levels of abstraction due to sparsity of data in multidimensional space. Strong associations discovered at high concept levels may represent common sense knowledge. However, what may represent common sense to one user may seem novel to another. Therefore, data mining systems should provide capabilities to mine association rules at multiple levels of abstraction and traverse easily among different abstraction spaces. P. Brezany Institut für Scientific Computing - Universität Wien 26

Multilevel (Generalized) Association Rules - Example Suppose we are given the following task-relevant set of transactional data for sales at the computer department of an All. Electronics branch, showing the items purchased for each transaction TID. Table Transactions TID T 1 T 2 T 3 T 4 T 5. . . P. Brezany Items purchased IBM desktop computer, Sony b/w printer Microsoft educational software, Microsoft financial software Logitech mouse computer accessory, Ergoway wrist pad accessory IBM desktop computer, Microsoft financial software IBM desktop computer. . . Institut für Scientific Computing - Universität Wien 27

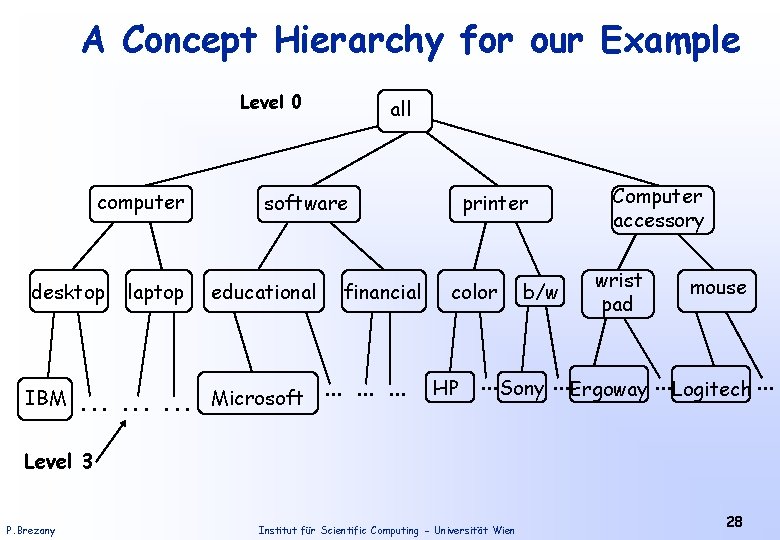
A Concept Hierarchy for our Example Level 0 computer desktop laptop all software educational financial IBM. . Microsoft. . printer color HP b/w Computer accessory wrist pad mouse . . . Sony. . . Ergoway. . . Logitech. . . Level 3 P. Brezany Institut für Scientific Computing - Universität Wien 28

Example (Cont. ) The items in Table Transactions are at the lowest level of the concept hierarchy. It is difficult to find interesting purchase patterns at such raw or primitive level data. If, e. g. , “IBM desktop computer” or “Sony b/w printer” each occurs in a very small fraction of the transactions, then it may be difficult to find strong associations involving such items. In other words, it is unlikely that the itemset “{IBM desktop computer, Sony b/w printer}” will satisfy minimum support. Itemsets containing generalized items, such as “{IBM desktop computer, b/w printer}” and “{computer, printer}” are more likely to have minimum support. Rules generated from association rule mining with concept hierarchies are called multiple-level or multilevel or generalized association rules. P. Brezany Institut für Scientific Computing - Universität Wien 29

Parallel Formulation of Association Rules • Need: – Huge Transaction Datasets (10 s of TB) – Large Number of Candidates. • Data Distribution: – Partition the Transaction Database, or – Partition the Candidates, or – Both P. Brezany Institut für Scientific Computing - Universität Wien 30

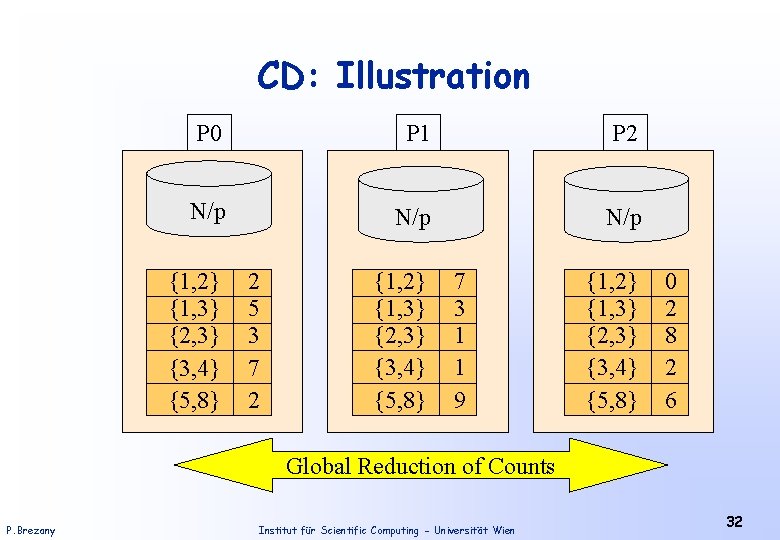
Parallel Association Rules: Count Distribution (CD) • Each Processor has complete candidate hash tree. • Each Processor updates its hash tree with local data. • Each Processor participates in global reduction to get global counts of candidates in the hash tree. • Multiple database scans per iteration are required if hash tree too big for memory. P. Brezany Institut für Scientific Computing - Universität Wien 31

CD: Illustration P 0 P 1 P 2 N/p N/p {1, 2} {1, 3} {2, 3} {3, 4} {5, 8} 2 5 3 7 2 {1, 2} {1, 3} {2, 3} {3, 4} {5, 8} 7 3 1 1 9 {1, 2} {1, 3} {2, 3} {3, 4} {5, 8} 0 2 8 2 6 Global Reduction of Counts P. Brezany Institut für Scientific Computing - Universität Wien 32

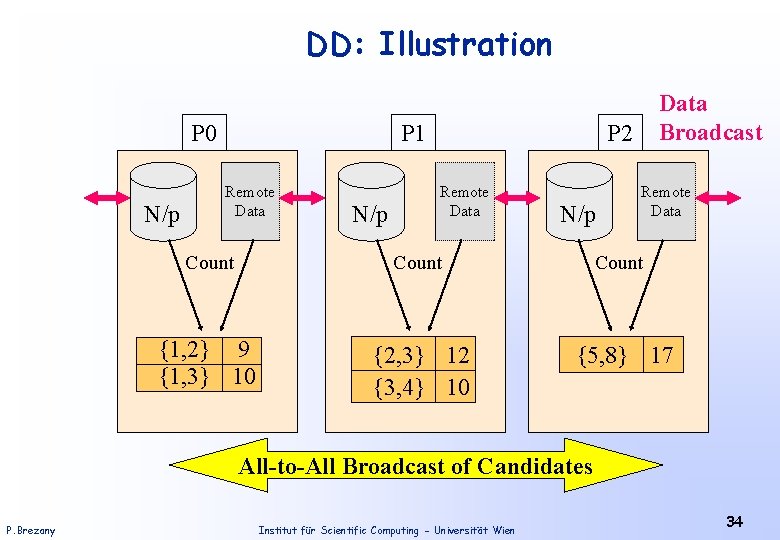
Parallel Association Rules: Data Distribution (DD) • Candidate set is partitioned among the processors. • Once local data has been partitioned, it is broadcast to all other processors. • High Communication Cost due to data movement. • Redundant work due to multiple traversals of the hash trees. P. Brezany Institut für Scientific Computing - Universität Wien 33

DD: Illustration P 0 N/p P 1 Remote Data N/p Data Broadcast P 2 Remote Data N/p Remote Data Count {1, 2} 9 {1, 3} 10 {2, 3} 12 {3, 4} 10 {5, 8} 17 All-to-All Broadcast of Candidates P. Brezany Institut für Scientific Computing - Universität Wien 34

Predictive Model Markup Language – PMML and Visualization P. Brezany Institut für Scientific Computing - Universität Wien 35

Predictive Model Markup Language PMML • Markup language (XML) to describe data mining models • PMML describes: – the inputs to data mining models – the transformations used prior to prepare data for data mining – The parameters which define the models themselves P. Brezany Institut für Scientific Computing - Universität Wien 36

PMML 2. 1 – Association Rules (1) 1. Model attributes (1) <xs: element name="Association. Model"> <xs: complex. Type> <xs: sequence> <xs: element min. Occurs="0" max. Occurs="unbounded" <xs: element ref="Mining. Schema" /> <xs: element min. Occurs="0" max. Occurs="unbounded" ref="Extension" /> ref="Itemset" /> ref="Association. Rule" /> <xs: element min. Occurs="0" max. Occurs="unbounded" ref="Extension" /> </xs: sequence> … P. Brezany Institut für Scientific Computing - Universität Wien 37

PMML 2. 1 – Association Rules (2) 1. Model attributes (2) <xs: attribute name="model. Name" type="xs: string" /> <xs: attribute name="function. Name" type="MINING-FUNCTION“ use="required"/> <xs: attribute name="algorithm. Name" type="xs: string" /> <xs: attribute name="number. Of. Transactions" type="INT-NUMBER" use="required" /> <xs: attribute name="max. Number. Of. Items. Per. TA" type="INT-NUMBER" /> <xs: attribute name="avg. Number. Of. Items. Per. TA" type="REAL-NUMBER" /> <xs: attribute name="minimum. Support" type="PROB-NUMBER" use="required" /> <xs: attribute name="minimum. Confidence" type="PROB-NUMBER" use="required" /> <xs: attribute name="length. Limit" type="INT-NUMBER" /> <xs: attribute name="number. Of. Items" type="INT-NUMBER" use="required" /> <xs: attribute name="number. Of. Itemsets" type="INT-NUMBER" use="required" /> <xs: attribute name="number. Of. Rules" type="INT-NUMBER" use="required" /> </xs: complex. Type> </xs: element> P. Brezany Institut für Scientific Computing - Universität Wien 38

PMML 2. 1 – Association Rules (3) 2. Items <xs: element name="Item"> <xs: complex. Type> <xs: attribute name="id" type="xs: string" use="required" /> <xs: attribute name="value" type="xs: string" use="required" /> <xs: attribute name="mapped. Value" type="xs: string" /> <xs: attribute name="weight" type="REAL-NUMBER" /> </xs: complex. Type> </xs: element> P. Brezany Institut für Scientific Computing - Universität Wien 39

PMML 2. 1 – Association Rules (4) 3. Item. Sets <xs: element name="Itemset"> <xs: complex. Type> <xs: sequence> <xs: element min. Occurs="0" max. Occurs="unbounded" ref="Item. Ref“ /> <xs: element min. Occurs="0" max. Occurs="unbounded" ref="Extension“ /> </xs: sequence> <xs: attribute name="id" type="xs: string" use="required" /> <xs: attribute name="support" type="PROB-NUMBER" /> <xs: attribute name="number. Of. Items" type="INT-NUMBER" /> </xs: complex. Type> </xs: element> P. Brezany Institut für Scientific Computing - Universität Wien 40

PMML 2. 1 – Association Rules (5) 4. Association. Rules <xs: element name="Association. Rule"> <xs: complex. Type> <xs: sequence> <xs: element min. Occurs="0" max. Occurs="unbounded" ref="Extension" /> </xs: sequence> <xs: attribute name="support" type="PROB-NUMBER" use="required" /> <xs: attribute name="confidence" type="PROB-NUMBER" use="required" /> <xs: attribute name="antecedent" type="xs: string" use="required" /> <xs: attribute name="consequent" type="xs: string" use="required" /> </xs: complex. Type> </xs: element> P. Brezany Institut für Scientific Computing - Universität Wien 41

PMML example model for Association. Rules (1) <? xml version="1. 0" ? > <PMML version="2. 1" > <Data. Dictionary number. Of. Fields="2" > <Data. Field name="transaction" optype="categorical" /> <Data. Field name="item" optype="categorical" /> </Data. Dictionary> <Association. Model function. Name="association. Rules" number. Of. Transactions="4" number. Of. Items=“ 4" minimum. Support="0. 6" minimum. Confidence="0. 3" number. Of. Itemsets=“ 7" number. Of. Rules=“ 3"> <Mining. Schema> <Mining. Field name="transaction"/> <Mining. Field name="item"/> </Mining. Schema> P. Brezany Institut für Scientific Computing - Universität Wien 42

PMML example model for Association. Rules (2) <!-- four items - input data --> <Item id="1" value=“PC" /> <Item id="2" value=“Monitor" /> <Item id="3" value=“Printer" /> <Item id=“ 4" value=“Notebook" /> <!-- three frequent 1 -itemsets --> <Itemset id="1" support="1. 0" number. Of. Items="1"> <Item. Ref item. Ref="1" /> </Itemset> <Itemset id="2" support="1. 0" number. Of. Items="1"> <Item. Ref item. Ref=“ 2" /> </Itemset> <Itemset id=“ 3" support="1. 0" number. Of. Items="1"> <Item. Ref item. Ref="3" /> </Itemset> P. Brezany Institut für Scientific Computing - Universität Wien 43

PMML example model for Association. Rules (3) <!-- three frequent 2 -itemset --> <Itemset id=“ 4" support="1. 0" number. Of. Items="2"> <Item. Ref item. Ref="1" /> <Item. Ref item. Ref=“ 2" /> </Itemset> <Itemset id=“ 5" support="1. 0" number. Of. Items="2"> <Item. Ref item. Ref="1" /> <Item. Ref item. Ref=“ 3" /> </Itemset> <Itemset id=“ 6" support="1. 0" number. Of. Items="2"> <Item. Ref item. Ref=“ 2" /> <Item. Ref item. Ref="3" /> </Itemset> P. Brezany Institut für Scientific Computing - Universität Wien 44

PMML example model for Association. Rules (4) <!-- one frequent 3 -itemset --> <Itemset id=“ 7" support="0. 9" number. Of. Items=“ 3"> <Item. Ref item. Ref="1" /> <Item. Ref item. Ref=“ 2" /> <Item. Ref item. Ref="3" /> </Itemset> <!-- three rules satisfy the requirements – the output --> <Association. Rule support="0. 9“ confidence="0. 85“ antecedent=“ 4" consequent=“ 3" /> <Association. Rule support="0. 9" confidence="0. 75" antecedent=“ 1" consequent=“ 6" /> <Association. Rule support="0. 9" confidence="0. 70" antecedent=“ 6" consequent="1" /> </Association. Model> </PMML> P. Brezany Institut für Scientific Computing - Universität Wien 45

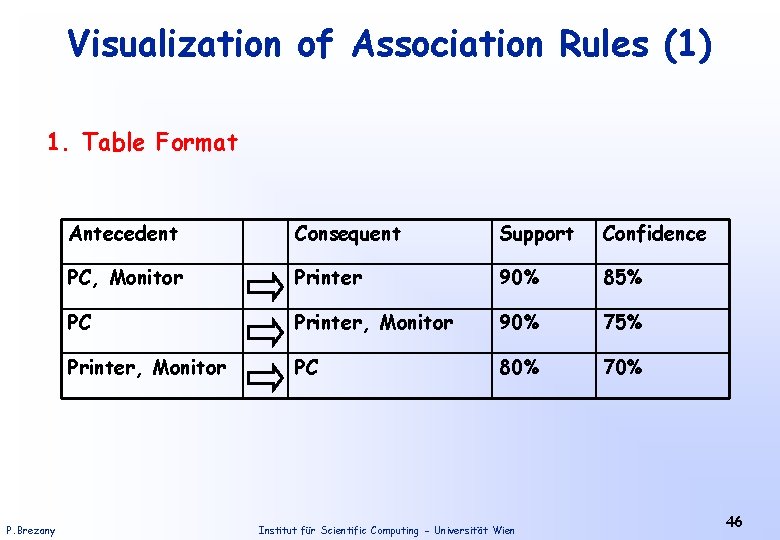
Visualization of Association Rules (1) 1. Table Format P. Brezany Antecedent Consequent Support Confidence PC, Monitor Printer 90% 85% PC Printer, Monitor 90% 75% Printer, Monitor PC 80% 70% Institut für Scientific Computing - Universität Wien 46

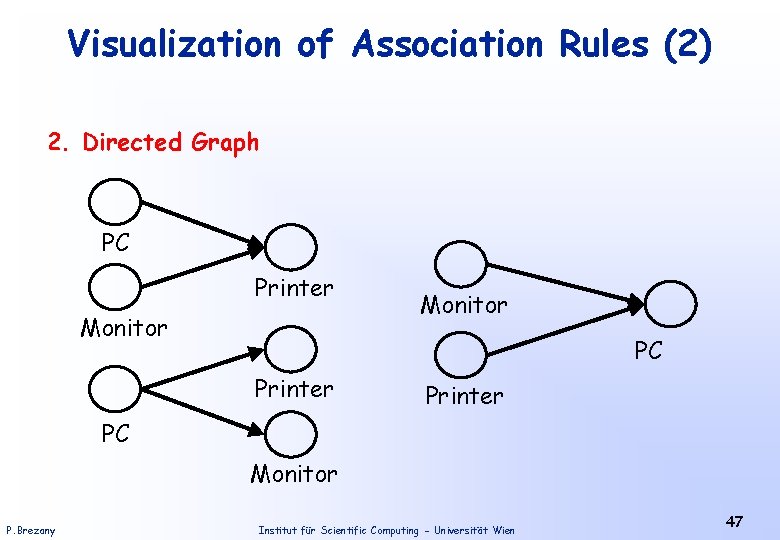
Visualization of Association Rules (2) 2. Directed Graph PC Printer Monitor PC Printer PC Monitor P. Brezany Institut für Scientific Computing - Universität Wien 47

Visualization of Association Rules (3) 3. 3 -D Visualisation P. Brezany Institut für Scientific Computing - Universität Wien 48

Mining Sequential Patterns (Mining Sequential Associations) P. Brezany Institut für Scientific Computing - Universität Wien 49

Mining Sequential Patterns • Discovering sequential patterns is a relatively new data mining problem. • The input data is a set of sequences, called datasequences. • Each data-sequence is a list of transactions where each transaction is a set of items. Typically, there is a transaction time associated with each transaction. • A sequential pattern also consists of a list of sets of items. • The problem is to find all sequential patterns with a user-specified minimum support , where the support of a sequential pattern is a percentage of data-sequences that contain the pattern. P. Brezany Institut für Scientific Computing - Universität Wien 50

Application Examples • Book club Each data sequence may correspond to all book selections of a customer, and each transaction corresponds to the books selected by the customer in one order. A sequential pattern may be “ 5% of customers bough `Foundation´, then `Foundation and Empire´ and then `Second Foundation´”. The data sequences corresponding to a customer who bought some other books in between these books still contains this sequential pattern. • Medical domain A data sequence may correspond to the symptoms or diseases of a patient, with a transaction corresponding to the symptoms exhibited or diseases diagnosed during a visit to the doctor. The patterns discovered could be used in disease research to help identify symptoms diseases that precede certain diseases. P. Brezany Institut für Scientific Computing - Universität Wien 51

Discovering Sequential Associations Given: A set of objects with associated event occurrences. events 2 1 1 5 9 3 Object 1 1 3 2 4 3 timeline 10 Object 2 P. Brezany 4 6 8 20 30 40 1 50 8 2 3 Institut für Scientific Computing - Universität Wien 52

Problem Statement We are given a database D of customer transactions. Each transaction consists of the following fields: customer-id, transaction-time, and the items purchased in the transaction. No customer has more than one transaction with the same transaction time. We do not consider quantities of items bought in a transaction: each item is a binary variable representing whether an item was bought or not. A sequence is an ordered list of itemsets. We denote an itemset i by (i 1 i 2. . . im ), where ij is an item. We denote a sequence s by <s 1 s 2. . . sn>, where sj is an itemset. A sequence <a 1 a 2. . . an> is contained in another sequence <b 1 b 2. . . bm> if there exist integers i 1 < i 2 < in such that a 1 bi 1, a 2 bi 2, . . . , an bin. P. Brezany Institut für Scientific Computing - Universität Wien 53

Problem Statement (2) For example, <(3) (4 5) (8)> is contained in <(7) (3 8) (9) (4 5 6) (8)>, since (3) (3 8), (4 5) (4 5 6) and (8). However, the sequence <(3) (5)> is not contained in <(3 5)> (an vice versa). The former represents items 3 and 5 being bought one after the other, while the latter represents items 3 and 5 being bought together. In a set of sequences, a sequence s is maximal if s is not contained in any other sequence. Customer sequence - an itemset list of customer transactions ordered by increasing transaction time: <itemset(T 1) itemset(T 2). . . itemset(Tn)> P. Brezany Institut für Scientific Computing - Universität Wien 54

Problem Statement (3) A customer supports a sequence s if s is contained in the customer sequence for this customer. The support for a sequence is defined as the fraction of total customers who support this sequence. Given a database D customer transactions, the problem of mining sequential patterns is to find the maximal sequences among all sequences that have a certain user-specified minimum support. Each such sequence represents a sequential pattern. We call a sequence satisfying the minimum support constraint a large sequence. See the next example. P. Brezany Institut für Scientific Computing - Universität Wien 55

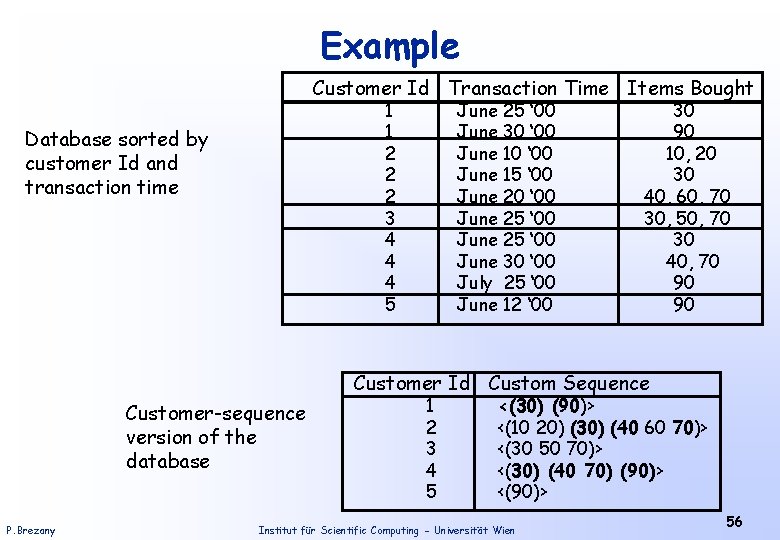
Example Customer Id Transaction Time Items Bought 1 1 2 2 2 3 4 4 4 5 Database sorted by customer Id and transaction time June 25 ‘ 00 June 30 ‘ 00 June 15 ‘ 00 June 20 ‘ 00 June 25 ‘ 00 June 30 ‘ 00 July 25 ‘ 00 June 12 ‘ 00 30 90 10, 20 30 40, 60, 70 30, 50, 70 30 40, 70 90 90 Customer Id Custom Sequence Customer-sequence version of the database P. Brezany 1 2 3 4 5 <(30) (90)> <(10 20) (30) (40 60 70)> <(30 50 70)> <(30) (40 70) (90)> <(90)> Institut für Scientific Computing - Universität Wien 56

Example (2) With minimum support set to 25%, i. e. , a minimum support of 2 customers, two sequences: <(30) (90)> and <(30) (40 70)> are maximal among those satisfying the support constraint, and are the desired sequential patterns. <(30) (90)> is supported by customers 1 and 4. Customer 4 buys items (40 70) in between items 30 and 90, but supports the patterns <(30) (90)> since we are looking for patterns that are not necessarily contiguous. <(30 (40 70)> is supported by customers 2 and 4. Customer 2 buys 60 along with 40 and 70, but suports this pattern since (40 70) is a subset of (40 60 70). E. g. the sequence <(10 20) (30)> does not have minimal support; it is only supported by customer 2. The sequences <(30)>, <(40)> <(70)>, <(90)>, <(30) (40)>, <(30) (70)> and <(40 70)> have minimum support, they are not maximal - therefore, they are not in the answer. 57 P. Brezany Institut für Scientific Computing - Universität Wien