DataLevel Parallelism in Vector SIMD and GPU Architectures

Data-Level Parallelism in Vector, SIMD, and GPU Architectures Copyright © 2012, Elsevier Inc. All rights reserved. 1

n Single instruction stream, single data stream (SISD) n Single instruction stream, multiple data streams (SIMD) n n Vector architectures Multimedia extensions Graphics processor units Multiple instruction streams, single data stream (MISD) n n Classes of Computers Flynn’s Taxonomy No commercial implementation Multiple instruction streams, multiple data streams (MIMD) n n Tightly-coupled MIMD Loosely-coupled MIMD Copyright © 2012, Elsevier Inc. All rights reserved. 2

n SIMD architectures can exploit significant datalevel parallelism for: n n n matrix-oriented scientific computing media-oriented image and sound processors SIMD is more energy efficient than MIMD n n n Introduction Only needs to fetch one instruction per data operation Makes SIMD attractive for personal mobile devices SIMD allows programmer to continue to think sequentially Copyright © 2012, Elsevier Inc. All rights reserved. 3

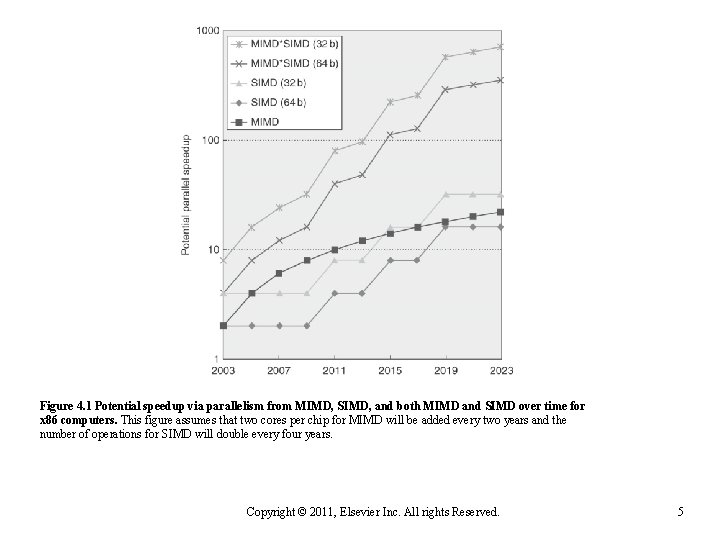
n Vector architectures SIMD extensions Graphics Processor Units (GPUs) n For x 86 processors: n n n Introduction SIMD Parallelism Expect two additional cores per chip per year SIMD width to double every four years Potential speedup from SIMD to be twice that from MIMD! Copyright © 2012, Elsevier Inc. All rights reserved. 4

Figure 4. 1 Potential speedup via parallelism from MIMD, SIMD, and both MIMD and SIMD over time for x 86 computers. This figure assumes that two cores per chip for MIMD will be added every two years and the number of operations for SIMD will double every four years. Copyright © 2011, Elsevier Inc. All rights Reserved. 5

n Basic idea: n n Read sets of data elements into “vector registers” Operate on those registers Disperse the results back into memory Vector Architectures Registers are controlled by compiler n n Used to hide memory latency Leverage memory bandwidth Copyright © 2012, Elsevier Inc. All rights reserved. 6

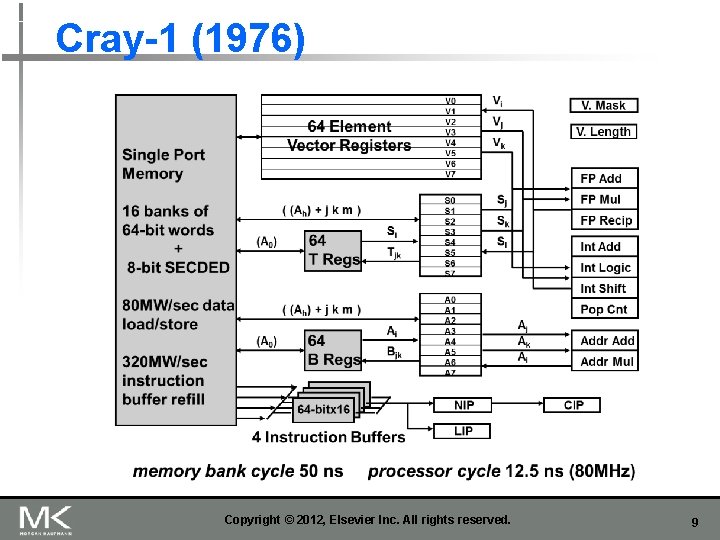
Vector Supercomputers n n n n n Epitomized by Cray-1, 1976: Scalar Unit + Vector Extensions Load/Store Architecture Vector Registers Vector Instructions Hardwired Control Highly Pipelined Functional Units Interleaved Memory System No Data Caches No Virtual Memory Copyright © 2012, Elsevier Inc. All rights reserved. 7

Cray 1 (1976) Copyright © 2012, Elsevier Inc. All rights reserved. 8

Cray 1 (1976) Copyright © 2012, Elsevier Inc. All rights reserved. 9

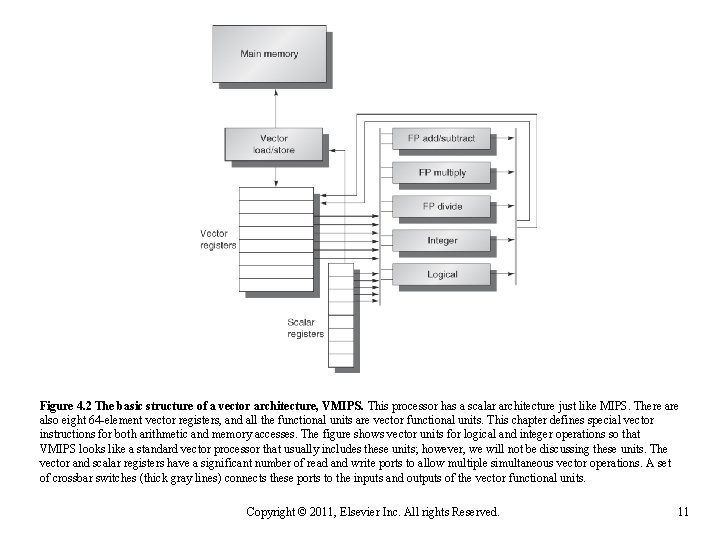
n Example architecture: VMIPS n n Loosely based on Cray-1 Vector registers n n Fully pipelined Data and control hazards are detected Vector load-store unit n n n Each register holds a 64 -element, 64 bits/element vector Register file has 16 read ports and 8 write ports Vector functional units n n Vector Architectures VMIPS Fully pipelined One word per clock cycle after initial latency Scalar registers n n 32 general-purpose registers 32 floating-point registers Copyright © 2012, Elsevier Inc. All rights reserved. 10

Figure 4. 2 The basic structure of a vector architecture, VMIPS. This processor has a scalar architecture just like MIPS. There also eight 64 -element vector registers, and all the functional units are vector functional units. This chapter defines special vector instructions for both arithmetic and memory accesses. The figure shows vector units for logical and integer operations so that VMIPS looks like a standard vector processor that usually includes these units; however, we will not be discussing these units. The vector and scalar registers have a significant number of read and write ports to allow multiple simultaneous vector operations. A set of crossbar switches (thick gray lines) connects these ports to the inputs and outputs of the vector functional units. Copyright © 2011, Elsevier Inc. All rights Reserved. 11

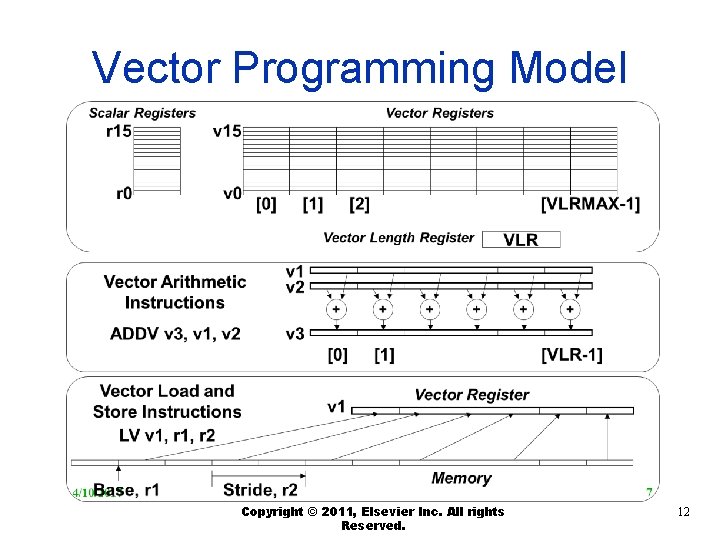
Vector Programming Model Copyright © 2011, Elsevier Inc. All rights Reserved. 12

n n n ADDVV. D: add two vectors ADDVS. D: add vector to a scalar LV/SV: vector load and vector store from address Vector Architectures VMIPS Instructions Example: DAXPY (double precision a*X+Y) L. D F 0, a ; load scalar a LV V 1, Rx ; load vector X MULVS. D V 2, V 1, F 0 ; vector-scalar multiply LV V 3, Ry ; load vector Y ADDVV V 4, V 2, V 3 ; add SV Ry, V 4 ; store the result Requires 6 instructions Copyright © 2012, Elsevier Inc. All rights reserved. 13

Example: DAXPY (double precision a*X+Y) Loop: n L. D DADDIU L. D MUL. D ADD. D S. D DADDIU SUBBU BNEZ F 0, a R 4, Rx, #512 F 2, 0(Rx) F 2, F 0 F 4, 0(Ry) F 4, F 2 F 4, 9(Ry) Rx, #8 Ry, #8 R 20, R 4, Rx R 20, Loop ; load scalar a ; last address to load ; load X[i] ; a x X[i] ; load Y[i] ; a x X[i] + Y[i] ; store into Y[i] ; increment index to X ; increment index to Y ; compute bound ; check if done Vector Architectures DAXPY in MIPS Instructions Requires almost 600 MIPS ops Copyright © 2012, Elsevier Inc. All rights reserved. 14

Vector Instruction Set Advantages Copyright © 2012, Elsevier Inc. All rights reserved. 15

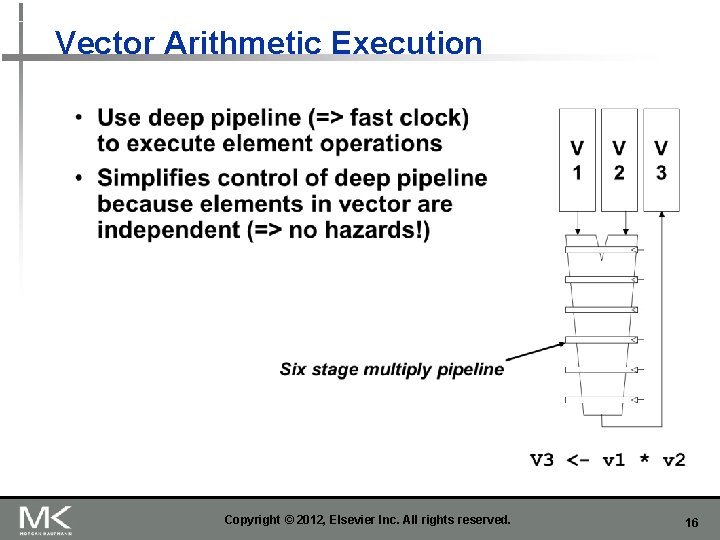
Vector Arithmetic Execution Copyright © 2012, Elsevier Inc. All rights reserved. 16

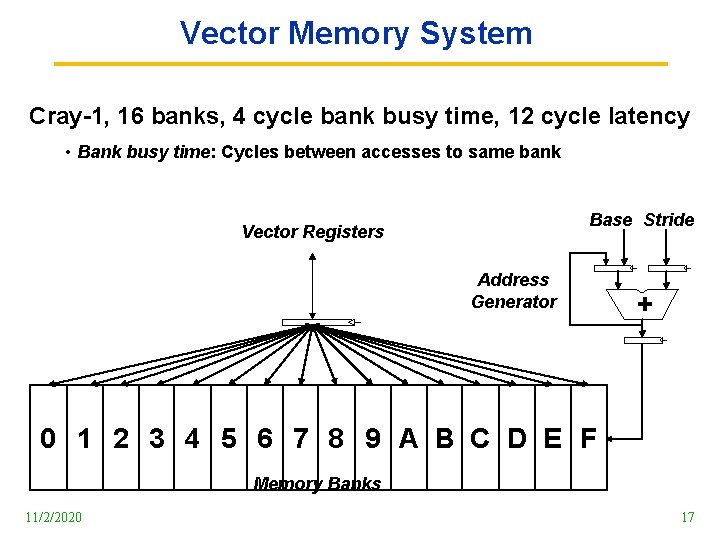
Vector Memory System Cray 1, 16 banks, 4 cycle bank busy time, 12 cycle latency • Bank busy time: Cycles between accesses to same bank Base Stride Vector Registers Address Generator + 0 1 2 3 4 5 6 7 8 9 A B C D E F Memory Banks 11/2/2020 17

n Execution time depends on three factors: n n VMIPS functional units consume one element per clock cycle n n Length of operand vectors Structural hazards Data dependencies Vector Architectures Vector Execution Time Execution time is approximately the vector length Convoy n Set of vector instructions that could potentially execute together Copyright © 2012, Elsevier Inc. All rights reserved. 18

n n Sequences with read-after-write dependency hazards can be in the same convoy via chaining Chaining n n Vector Architectures Chimes Allows a vector operation to start as soon as the individual elements of its vector source operand become available Chime n n n Unit of time to execute one convoy m convoys executes in m chimes For vector length of n, requires m x n clock cycles Copyright © 2012, Elsevier Inc. All rights reserved. 19

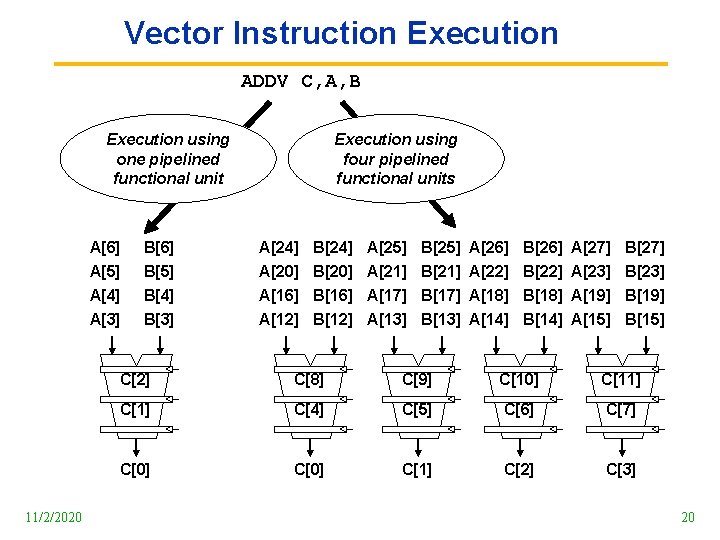
Vector Instruction Execution ADDV C, A, B Execution using one pipelined functional unit 11/2/2020 Execution using four pipelined functional units A[6] B[6] A[24] B[24] A[25] B[25] A[26] B[26] A[27] B[27] A[5] A[4] A[3] B[5] B[4] B[3] A[20] B[20] A[21] B[21] A[22] B[22] A[23] B[23] A[16] B[16] A[17] B[17] A[18] B[18] A[19] B[19] A[12] B[12] A[13] B[13] A[14] B[14] A[15] B[15] C[2] C[8] C[9] C[10] C[11] C[4] C[5] C[6] C[7] C[0] C[1] C[2] C[3] 20

Automatic Code Vectorization for (i=0; i < N; i++) C[i] = A[i] + B[i]; Vectorized Code Scalar Sequential Code load Iter. 1 add store load Iter. 2 add 11/2/2020 store load Time load Iter. 1 load add store Iter. 2 Vector Instruction Vectorization is a massive compile time reordering of operation sequencing requires extensive loop dependence analysis 21

Vector Stripmining Problem: Vector registers have finite length Solution: Break loops into pieces that fit into vector registers, “Stripmining” 11/2/2020 22

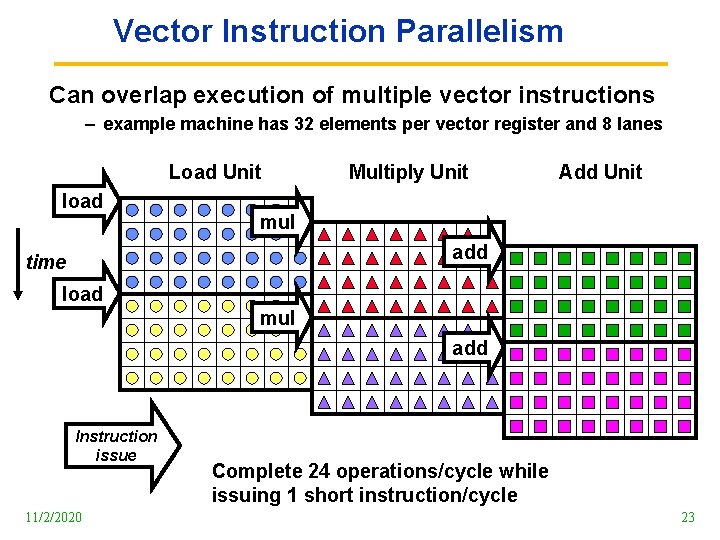
Vector Instruction Parallelism Can overlap execution of multiple vector instructions – example machine has 32 elements per vector register and 8 lanes Load Unit load Multiply Unit Add Unit mul add time load mul add Instruction issue 11/2/2020 Complete 24 operations/cycle while issuing 1 short instruction/cycle 23

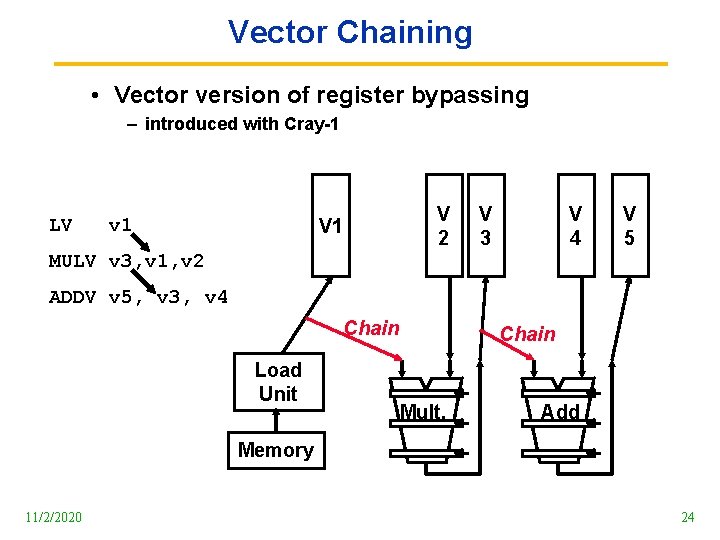
Vector Chaining • Vector version of register bypassing – introduced with Cray 1 LV v 1 V 2 V 1 V 3 V 4 V 5 MULV v 3, v 1, v 2 ADDV v 5, v 3, v 4 Chain Load Unit Chain Mult. Add Memory 11/2/2020 24

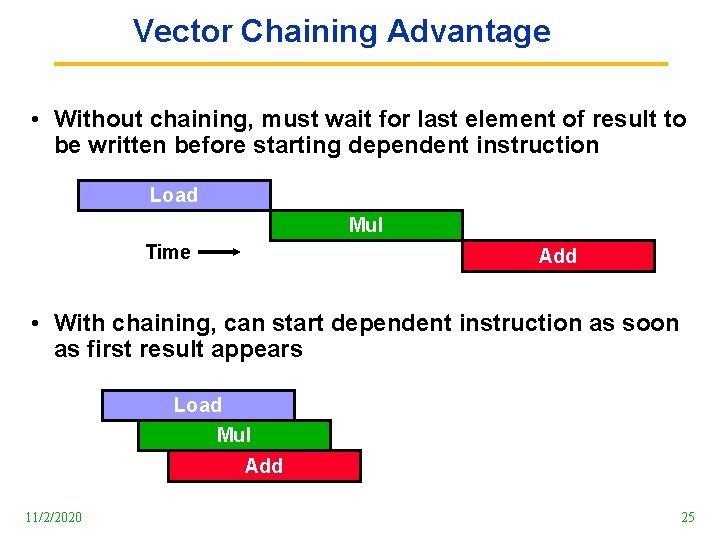
Vector Chaining Advantage • Without chaining, must wait for last element of result to be written before starting dependent instruction Load Mul Time Add • With chaining, can start dependent instruction as soon as first result appears Load Mul Add 11/2/2020 25

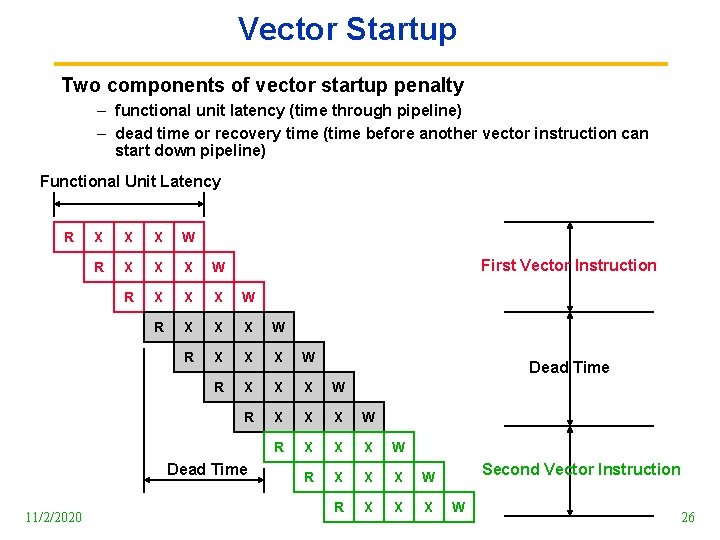
Vector Startup Two components of vector startup penalty – functional unit latency (time through pipeline) – dead time or recovery time (time before another vector instruction can start down pipeline) Functional Unit Latency R X X X W R X X X W R X X X W R X X X First Vector Instruction Dead Time 11/2/2020 Dead Time Second Vector Instruction W 26

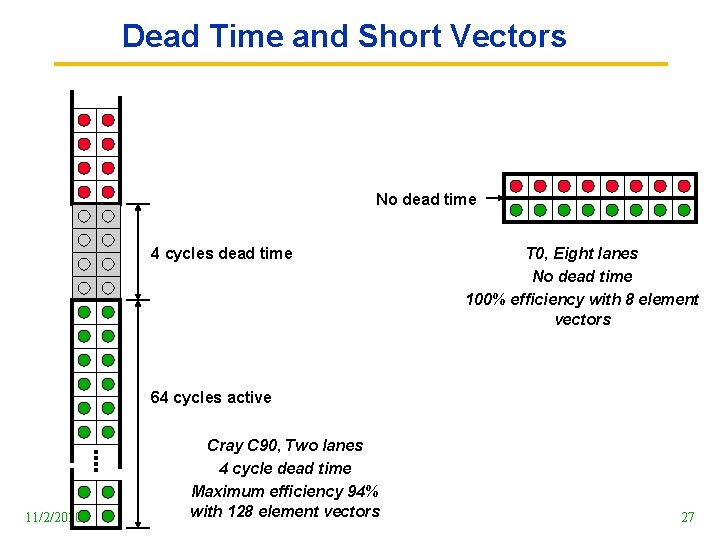
Dead Time and Short Vectors No dead time 4 cycles dead time T 0, Eight lanes No dead time 100% efficiency with 8 element vectors 64 cycles active 11/2/2020 Cray C 90, Two lanes 4 cycle dead time Maximum efficiency 94% with 128 element vectors 27

Vector Scatter/Gather Want to vectorize loops with indirect accesses: for (i=0; i<N; i++) A[i] = B[i] + C[D[i]] Indexed load instruction (Gather) LV v. D, r. D # Load indices in D vector LVI v. C, r. C, v. D # Load indirect from r. C base LV v. B, r. B # Load B vector ADDV. D v. A, v. B, v. C # Do add SV v. A, r. A # Store result 11/2/2020 28

Vector Scatter/Gather Scatter example: for (i=0; i<N; i++) A[B[i]]++; Is following a correct translation? LV v. B, r. B LVI v. A, r. A, v. B ADDV v. A, 1 SVI v. A, r. A, v. B 11/2/2020 # # Load indices in B vector Gather initial A values Increment Scatter incremented values 29

Vector Conditional Execution Problem: Want to vectorize loops with conditional code: for (i=0; i<N; i++) if (A[i]>0) then A[i] = B[i]; Solution: Add vector mask (or flag) registers – vector version of predicate registers, 1 bit per element …and maskable vector instructions – vector operation becomes NOP at elements where mask bit is clear Code example: CVM LV v. A, r. A SGTVS. D v. A, F 0 LV v. A, r. B SV v. A, r. A 11/2/2020 # # # Turn on all elements Load entire A vector Set bits in mask register where A>0 Load B vector into A under mask Store A back to memory under mask 30

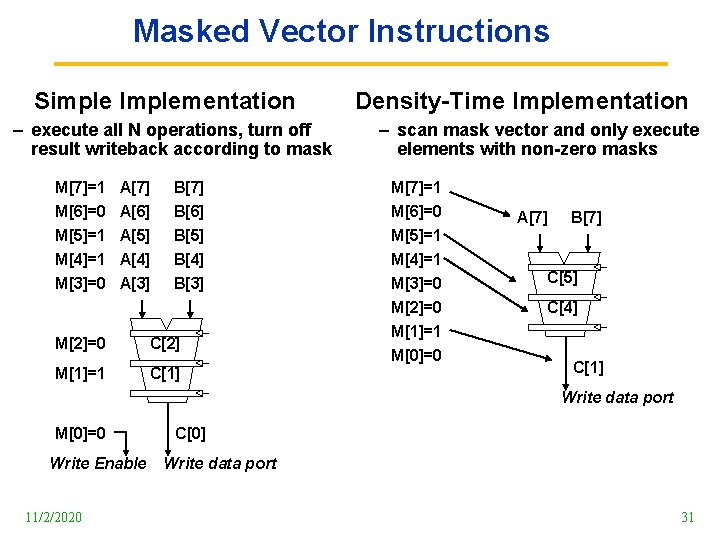
Masked Vector Instructions Simple Implementation – execute all N operations, turn off result writeback according to mask Density Time Implementation – scan mask vector and only execute elements with non zero masks M[7]=1 A[7] B[7] M[7]=1 M[6]=0 M[5]=1 M[4]=1 M[3]=0 B[6] B[5] B[4] B[3] M[6]=0 M[5]=1 M[4]=1 M[3]=0 M[2]=0 M[1]=1 M[0]=0 A[6] A[5] A[4] A[3] M[2]=0 C[2] M[1]=1 C[1] A[7] B[7] C[5] C[4] C[1] Write data port M[0]=0 Write Enable 11/2/2020 C[0] Write data port 31

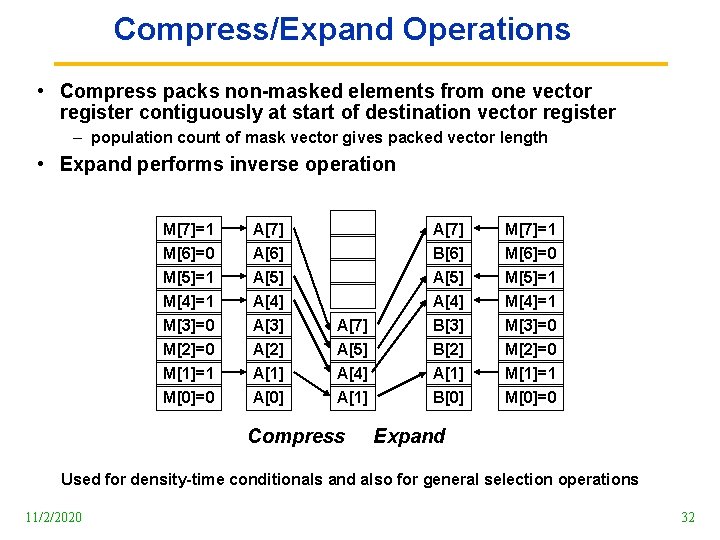
Compress/Expand Operations • Compress packs non masked elements from one vector register contiguously at start of destination vector register – population count of mask vector gives packed vector length • Expand performs inverse operation M[7]=1 A[7] M[6]=0 M[5]=1 M[4]=1 M[3]=0 M[2]=0 M[1]=1 M[0]=0 A[6] A[5] A[4] A[3] A[2] A[1] A[0] A[7] A[5] A[4] A[1] Compress A[7] B[6] A[5] A[4] B[3] B[2] A[1] B[0] M[7]=1 M[6]=0 M[5]=1 M[4]=1 M[3]=0 M[2]=0 M[1]=1 M[0]=0 Expand Used for density time conditionals and also for general selection operations 11/2/2020 32

LV MULVS. D LV ADDVV. D SV Convoys: 1 LV 2 LV 3 SV V 1, Rx V 2, V 1, F 0 V 3, Ry V 4, V 2, V 3 Ry, V 4 ; load vector X ; vector-scalar multiply ; load vector Y ; add two vectors ; store the sum Vector Architectures Example: Convoys and Chimes MULVS. D ADDVV. D 3 chimes, 2 FP ops per result, cycles per FLOP = 1. 5 For 64 element vectors, requires 64 x 3 = 192 clock cycles Copyright © 2012, Elsevier Inc. All rights reserved. 33

n Start up time n n Latency of vector functional unit Assume the same as Cray-1 n n n Floating-point add => 6 clock cycles Floating-point multiply => 7 clock cycles Floating-point divide => 20 clock cycles Vector load => 12 clock cycles Vector Architectures Challenges Optimizations: n n n n Multiple Lanes: > 1 element per clock cycle Vector Length Registers: Non-64 wide vectors Vector Mask Registers: IF statements in vector code Memory Banks: Memory system optimizations to support vector processors Stride: Multiple dimensional matrices Scatter-Gather: Sparse matrices Programming Vector Architectures: Program structures affecting performance Copyright © 2012, Elsevier Inc. All rights reserved. 34

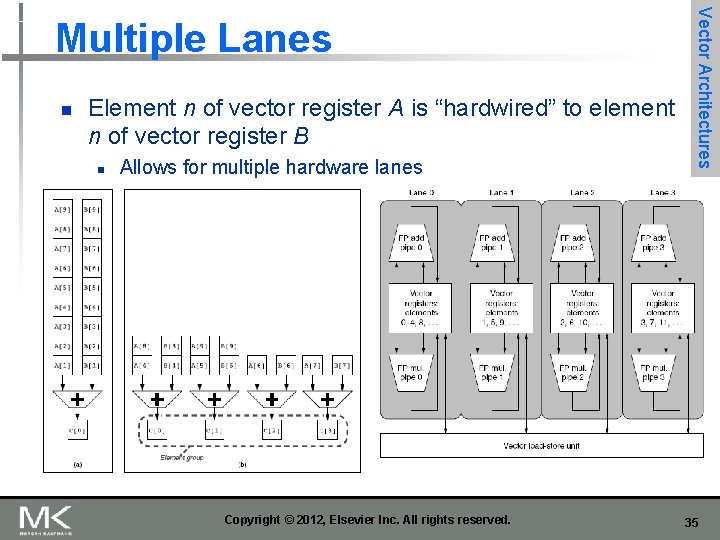
n Element n of vector register A is “hardwired” to element n of vector register B n Allows for multiple hardware lanes Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Multiple Lanes 35

n n n Vector length not known at compile time? Use Vector Length Register (VLR) Use strip mining for vectors over the maximum length: Vector Architectures Vector Length Registers low = 0; VL = (n % MVL); /*find odd-size piece using modulo op % */ for (j = 0; j <= (n/MVL); j=j+1) { /*outer loop*/ for (i = low; i < (low+VL); i=i+1) /*runs for length VL*/ Y[i] = a * X[i] + Y[i] ; /*main operation*/ low = low + VL; /*start of next vector*/ VL = MVL; /*reset the length to maximum vector length*/ } Copyright © 2012, Elsevier Inc. All rights reserved. 36

n n Consider: for (i = 0; i < 64; i=i+1) if (X[i] != 0) X[i] = X[i] – Y[i]; Use vector mask register to “disable” elements (if conversion): LV LV L. D SNEVS. D SUBVV. D SV n V 1, Rx V 2, Ry F 0, #0 V 1, F 0 V 1, V 2 Rx, V 1 Vector Architectures Vector Mask Registers ; load vector X into V 1 ; load vector Y ; load FP zero into F 0 ; sets VM(i) to 1 if V 1(i)!=F 0 ; subtract under vector mask ; store the result in X GFLOPS rate decreases! Copyright © 2012, Elsevier Inc. All rights reserved. 37

n n Memory system must be designed to support high bandwidth for vector loads and stores Spread accesses across multiple banks n n Vector Architectures Memory Banks Control bank addresses independently Load or store non sequential words Support multiple vector processors sharing the same memory Example: n n n 32 processors, each generating 4 loads and 2 stores/cycle Processor cycle time is 2. 167 ns, SRAM cycle time is 15 ns How many memory banks needed? n n n 32 x 6=192 accesses, 15/2. 167≈7 processor cycles 1344! Copyright © 2012, Elsevier Inc. All rights reserved. 38

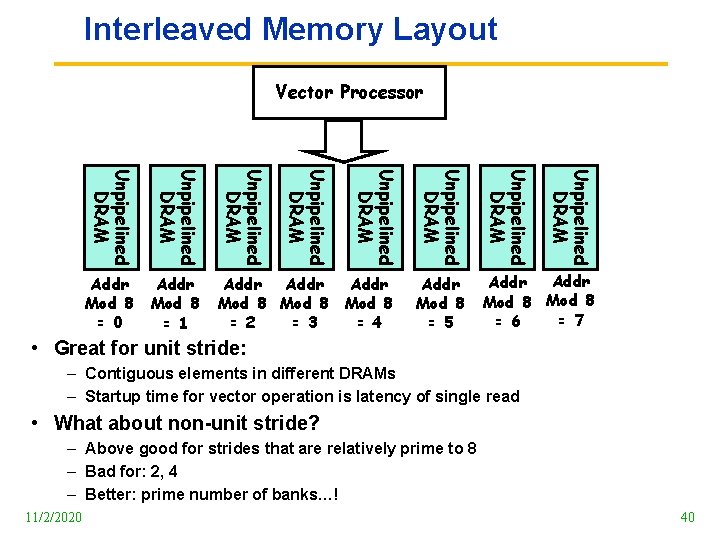
Memory operations • Load/store operations move groups of data between registers and memory • Three types of addressing – Unit stride » Contiguous block of information in memory » Fastest: always possible to optimize this – Non unit (constant) stride » Harder to optimize memory system for all possible strides » Prime number of data banks makes it easier to support different strides at full bandwidth – Indexed (gather scatter) » Vector equivalent of register indirect » Good for sparse arrays of data » Increases number of programs that vectorize 11/2/2020 39

Interleaved Memory Layout Vector Processor Unpipelined DRAM Addr Mod 8 = 5 Addr Mod 8 = 7 = 6 Unpipelined DRAM Addr Mod 8 = 2 = 3 = 4 Unpipelined DRAM Addr Mod 8 = 1 Unpipelined DRAM Addr Mod 8 = 0 • Great for unit stride: – Contiguous elements in different DRAMs – Startup time for vector operation is latency of single read • What about non unit stride? – Above good for strides that are relatively prime to 8 – Bad for: 2, 4 – Better: prime number of banks…! 11/2/2020 40

n n Consider: for (i = 0; i < 100; i=i+1) for (j = 0; j < 100; j=j+1) { A[i][j] = 0. 0; for (k = 0; k < 100; k=k+1) A[i][j] = A[i][j] + B[i][k] * D[k][j]; } Vector Architectures Stride Must vectorize multiplication of rows of B with columns of D Use non-unit stride Bank conflict (stall) occurs when the same bank is hit faster than bank busy time: n #banks / LCM(stride, #banks) < bank busy time (in # of cycles) Copyright © 2012, Elsevier Inc. All rights reserved. 41

n n Example: 8 memory banks with a bank busy time of 6 cycles and a total memory latency of 12 cycles. How long will it take to complete a 64 element vector load with a stride of 1? With a stride of 32? Answer: n n Vector Architectures Stride of 1: number of banks is greater than the bank busy time, so it takes n 12+64 = 76 clock cycles 1. 2 cycle per element Stride of 32: the worst case scenario happens when the stride value is a multiple of the number of banks, which this is! Every access to memory will collide with the previous one! Thus, the total time will be: n 12 + 1 + 6 * 63 = 391 clock cycles, or 6. 1 clock cycles per element! Copyright © 2012, Elsevier Inc. All rights reserved. 42

Consider sparse vectors A & C and vector indices K & M, and A and C have the same number (n) of non-zeros: for (i = 0; i < n; i=i+1) A[K[i]] = A[K[i]] + C[M[i]]; Ra, Rc, Rk and Rm the starting addresses of vectors n Use index vector: LV Vk, Rk ; load K LVI Va, (Ra+Vk) ; load A[K[]] LV Vm, Rm ; load M LVI Vc, (Rc+Vm) ; load C[M[]] ADDVV. D Va, Vc ; add them SVI (Ra+Vk), Va ; store A[K[]] n Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Scatter Gather 43

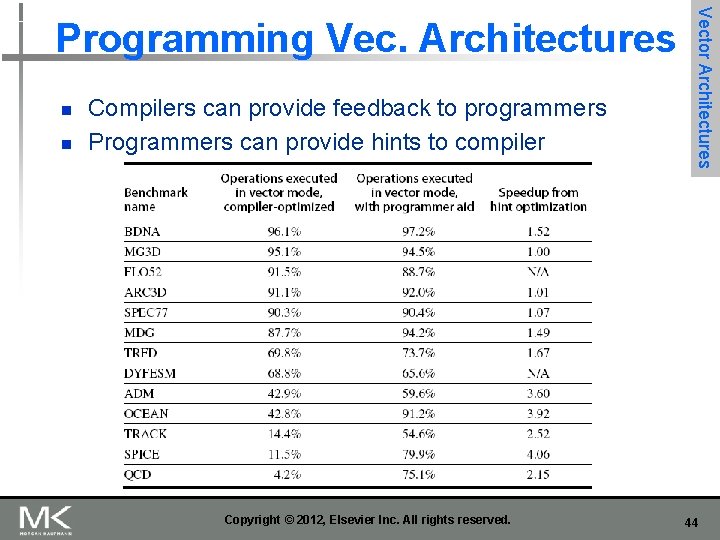
n n Compilers can provide feedback to programmers Programmers can provide hints to compiler Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Programming Vec. Architectures 44

n Optimizations: n Multiple Lanes: > 1 element per clock cycle n Vector Length Registers: Non-64 wide vectors n Vector Mask Registers: IF statements in vector code n Memory Banks: Memory system optimizations to support vector processors n Stride: Multiple dimensional matrices n Scatter-Gather: Sparse matrices n Programming Vector Architectures: Program structures affecting performance Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Summary of Vector Architecture 45

Properties of Vector Processors • Each result independent of previous result => long pipeline, compiler ensures no dependencies => high clock rate • Vector instructions access memory with known pattern => highly interleaved memory => amortize memory latency of over 64 elements => no (data) caches required! (Do use instruction cache) • Reduces branches and branch problems in pipelines • Single vector instruction implies lots of work ( loop) => fewer instruction fetches 11/2/2020 46

Advantages n n Vectors are inexpensive (O(N+εN 2) circuitry) Vectors lower power n n One fetch and decode per instruction Smaller code Vector unit switches off when not in use Vector instructions expose parallelism without speculation Copyright © 2012, Elsevier Inc. All rights reserved. 47

Vector Architectures In class exercise n Consider the following code, which multiplies two vectors that contain single-precision complex values: For (i=0; i<300; i++) { c_re[i] = a_re[i] * b_re[i] – a_im[i] * b_im[i]; c_im[i] = a_re[i] * b_im[i] – a_im[i] * b_re[i]; Asumme that the processor runs at 700 MHz and has a maximum vector length of 64. A. B. C. What is the arithmetic intensity of this kernel (i. e. , the ratio of floating point operations per byte of memory accessed)? Convert this loop into VMIPS assembly code using strip mining. Assuming chaining and a single memory pipeline, how many chimes are required? Copyright © 2012, Elsevier Inc. All rights reserved. 48

A. B. This code reads four floats and writes two floats for every six FLOPs, so the arithmetic intensity = 6/6 = 1. Assume MVL = 64 300 mod 64 = 44 Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures In class exercise 49

C. Identify convoys: 1. mulvv. s lv 2. lv mulvv. s 3. subvv. s sv 4. mulvv. s lv 5. mulvv. s lv 6. addvv. s sv # a_re * b_re # (assume already loaded), # load a_im # load b_im, a_im * b_im # subtract and store c_re # a_re * b_re, # load next a_re vector # a_im * b_re, # load next b_re vector # add and store c_im Vector Architectures In class exercise 6 chimes Copyright © 2012, Elsevier Inc. All rights reserved. 50

n n Media applications operate on data types narrower than the native word size n Example: disconnect carry chains to “partition” adder Limitations, compared to vector instructions: n Number of data operands encoded into op code n No sophisticated addressing modes (strided, scattergather) n No mask registers Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia SIMD Extensions 51

n Implementations: n Intel MMX (1996) n n Streaming SIMD Extensions (SSE) (1999) n n n Eight 16 -bit integer ops Four 32 -bit integer/fp ops or two 64 -bit integer/fp ops Advanced Vector Extensions (2010) n n Eight 8 -bit integer ops or four 16 -bit integer ops Four 64 -bit integer/fp ops Operands must be consecutive and aligned memory locations Generally designed to accelerate carefully written libraries rather than for compilers Advantages over vector architecture: n n SIMD Instruction Set Extensions for Multimedia SIMD Implementations Cost little to add to the standard ALU and easy to implement Require little extra state easy for context-switch Require little extra memory bandwidth No virtual memory problem of cross-page access and page-fault Copyright © 2012, Elsevier Inc. All rights reserved. 52

n Example DXPY: L. D MOV MOV DADDIU Loop: MUL. 4 D ADD. 4 D S. 4 D DADDIU DSUBU BNEZ F 0, a F 1, F 0 F 2, F 0 F 3, F 0 R 4, Rx, #512 L. 4 D F 4, 0[Rx] F 4, F 0 F 4, F 4 F 8, 0[Ry] F 8, F 4 F 8, 0[Ry] F 8 Rx, #32 Ry, #32 R 20, R 4, Rx R 20, Loop ; load scalar a ; copy a into F 1 for SIMD MUL ; copy a into F 2 for SIMD MUL ; copy a into F 3 for SIMD MUL ; last address to load ; load X[i], X[i+1], X[i+2], X[i+3] ; a×X[i], a×X[i+1], a×X[i+2], a×X[i+3] ; load Y[i], Y[i+1], Y[i+2], Y[i+3] ; a×X[i]+Y[i], . . . , a×X[i+3]+Y[i+3] ; store into Y[i], Y[i+1], Y[i+2], Y[i+3] ; increment index to X ; increment index to Y ; compute bound ; check if done Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Example SIMD Code 53

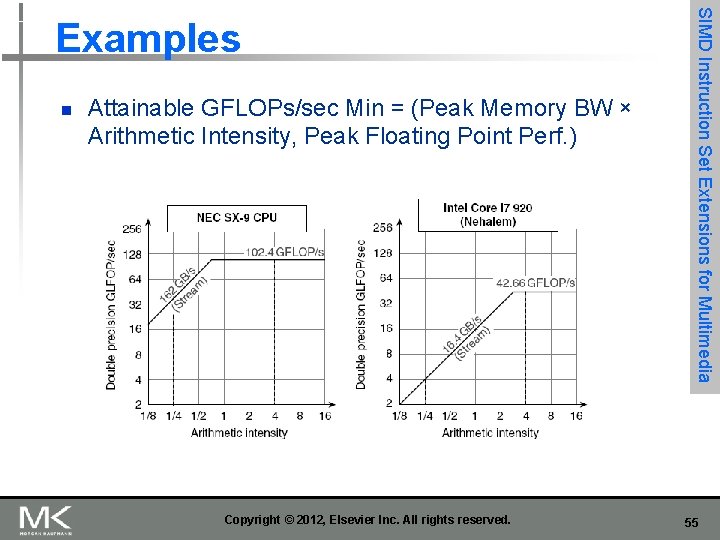
n n Basic idea: n Plot peak floating-point throughput as a function of arithmetic intensity n Ties together floating-point performance and memory performance for a target machine Arithmetic intensity n Floating-point operations per byte read Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Roofline Performance Model 54

n Attainable GFLOPs/sec Min = (Peak Memory BW × Arithmetic Intensity, Peak Floating Point Perf. ) Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Examples 55

n n Given the hardware invested to do graphics well, how can it be supplemented to improve performance of a wider range of applications? Basic idea: n Heterogeneous execution model n n CPU is the host, GPU is the device Develop a C-like programming language for GPU n n Graphical Processing Units Compute Unified Device Architecture (CUDA) Open. CL for vendor-independent language Unify all forms of GPU parallelism as CUDA thread Programming model is “Single Instruction Multiple Thread” (SIMT) Copyright © 2012, Elsevier Inc. All rights reserved. 56

n A thread is associated with each data element n n Threads are organized into blocks n n n Thread Blocks: groups of up to 512 elements Multithreaded SIMD Processor: hardware that executes a whole thread block (32 elements executed per thread at a time) Blocks are organized into a grid n n n CUDA threads, with thousands of which being utilized to various styles of parallelism: multithreading, SIMD, MIMD, ILP Graphical Processing Units Threads and Blocks are executed independently and in any order Different blocks cannot communicate directly but can coordinate using atomic memory operations in Global Memory GPU hardware handles thread management, not applications or OS n n A multiprocessor composed of multithreaded SIMD processors A Thread Block Scheduler Copyright © 2012, Elsevier Inc. All rights reserved. 57

Copyright © 2012, Elsevier Inc. All rights reserved. Graphical Processing Units Grid, Threads, and Blocks 58

n Similarities to vector machines: n n n Works well with data-level parallel problems Scatter-gather transfers Mask registers Large register files Graphical Processing Units NVIDIA GPU Architecture Differences: n n n No scalar processor Uses multithreading to hide memory latency Has many functional units, as opposed to a few deeply pipelined units like a vector processor Copyright © 2012, Elsevier Inc. All rights reserved. 59

n Multiply two vectors of length 8192 n n Code that works over all elements is the grid Thread blocks break this down into manageable sizes n n n 512 elements/block, 16 SIMD threads/block 32 ele/thread Graphical Processing Units Example SIMD instruction executes 32 elements at a time Thus grid size = 16 blocks Block is analogous to a strip-mined vector loop with vector length of 32 Block is assigned to a multithreaded SIMD processor by the thread block scheduler Current-generation GPUs (Fermi) have 7 -15 multithreaded SIMD processors Copyright © 2012, Elsevier Inc. All rights reserved. 60

Figure 4. 15 Floor plan of the Fermi GTX 480 GPU. This diagram shows 16 multithreaded SIMD Processors. The Thread Block Scheduler is highlighted on the left. The GTX 480 has 6 GDDR 5 ports, each 64 bits wide, supporting up to 6 GB of capacity. The Host Interface is PCI Express 2. 0 x 16. Giga Thread is the name of the scheduler that distributes thread blocks to Multiprocessors, each of which has its own SIMD Thread Scheduler. Copyright © 2011, Elsevier Inc. All rights Reserved. 61

n Threads of SIMD instructions n n Each has its own PC Thread scheduler uses scoreboard to dispatch No data dependencies between threads! Keeps track of up to 48 threads of SIMD instructions n n n Graphical Processing Units Terminology Hides memory latency Thread block scheduler schedules blocks to SIMD processors Within each SIMD processor: n n 32 SIMD lanes Wide and shallow compared to vector processors Copyright © 2012, Elsevier Inc. All rights reserved. 62

Figure 4. 16 Scheduling of threads of SIMD instructions. The scheduler selects a ready thread of SIMD instructions and issues an instruction synchronously to all the SIMD Lanes executing the SIMD thread. Because threads of SIMD instructions are independent, the scheduler may select a different SIMD thread each time. Copyright © 2011, Elsevier Inc. All rights Reserved. 63

n NVIDIA GPU has 32, 768 registers n n n Divided into lanes Each SIMD thread is limited to 64 registers SIMD thread has up to: n n n Graphical Processing Units Example 64 vector registers of 32 32 -bit elements 32 vector registers of 32 64 -bit elements Fermi has 16 physical SIMD lanes, each containing 2048 registers Copyright © 2012, Elsevier Inc. All rights reserved. 64

Figure 4. 14 Simplified block diagram of a Multithreaded SIMD Processor. It has 16 SIMD lanes. The SIMD Thread Scheduler has, say, 48 independentthreads of SIMD instructions that it schedules with a table of 48 PCs. Copyright © 2011, Elsevier Inc. All rights Reserved. 65

n ISA is an abstraction of the hardware instruction set n n “Parallel Thread Execution (PTX)” Uses virtual registers Translation to machine code is performed in software Example: one CUDA thread, 8192 of these created! Graphical Processing Units NVIDIA Instruction Set Arch. shl. s 32 R 8, block. Idx, 9 ; Thread Block ID * Block size (512 or 29) add. s 32 R 8, thread. Idx ; R 8 = i = my CUDA thread ID ld. global. f 64 RD 0, [X+R 8] ; RD 0 = X[i] ld. global. f 64 RD 2, [Y+R 8] ; RD 2 = Y[i] mul. f 64 R 0 D, RD 0, RD 4 ; Product in RD 0 = RD 0 * RD 4 (scalar a) add. f 64 R 0 D, RD 0, RD 2 ; Sum in RD 0 = RD 0 + RD 2 (Y[i]) st. global. f 64 [Y+R 8], RD 0 ; Y[i] = sum (X[i]*a + Y[i]) Copyright © 2012, Elsevier Inc. All rights reserved. 66

n n Like vector architectures, GPU branch hardware uses internal masks Also uses n Branch synchronization stack n n n Instruction markers to manage when a branch diverges into multiple execution paths n n Push on divergent branch …and when paths converge n n n Entries consist of masks for each SIMD lane I. e. which threads commit their results (all threads execute) Graphical Processing Units Conditional Branching Act as barriers Pops stack Per-thread-lane 1 -bit predicate register, specified by programmer Copyright © 2012, Elsevier Inc. All rights reserved. 67

if (X[i] != 0) X[i] = X[i] – Y[i]; else X[i] = Z[i]; ld. global. f 64 setp. neq. s 32 @!P 1, bra RD 0, [X+R 8] P 1, RD 0, #0 ELSE 1, *Push ; RD 0 = X[i] ; P 1 is predicate register 1 ; Push old mask, set new mask bits ; if P 1 false, go to ELSE 1 ld. global. f 64 RD 2, [Y+R 8] ; RD 2 = Y[i] sub. f 64 RD 0, RD 2 ; Difference in RD 0 st. global. f 64 [X+R 8], RD 0 ; X[i] = RD 0 @P 1, bra ENDIF 1, *Comp ; complement mask bits ; if P 1 true, go to ENDIF 1 ELSE 1: ld. global. f 64 RD 0, [Z+R 8] ; RD 0 = Z[i] st. global. f 64 [X+R 8], RD 0 ; X[i] = RD 0 ENDIF 1: <next instruction>, *Pop ; pop to restore old mask Copyright © 2012, Elsevier Inc. All rights reserved. Graphical Processing Units Example 68

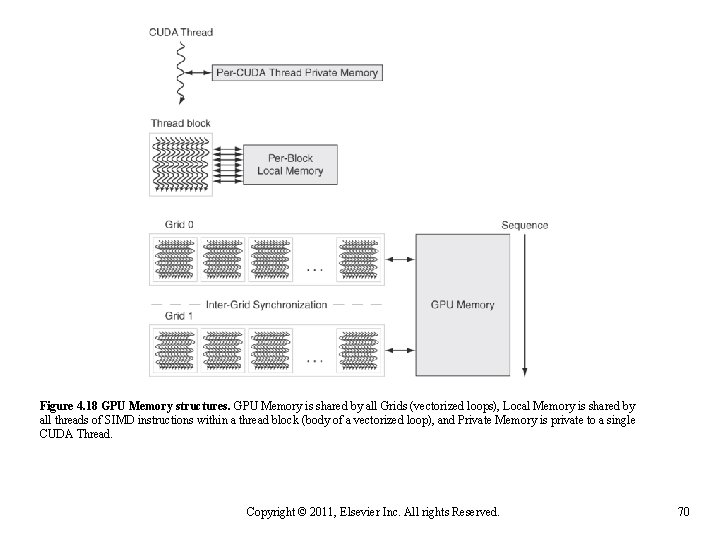
n n Each SIMD Lane has private section of off-chip DRAM n “Private memory”, not shared by any other lanes n Contains stack frame, spilling registers, and private variables n Recent GPUs cache this in L 1 and L 2 caches Each multithreaded SIMD processor also has local memory that is on-chip n n Graphical Processing Units NVIDIA GPU Memory Structures Shared by SIMD lanes / threads within a block only The off-chip memory shared by SIMD processors is GPU Memory n Host can read and write GPU memory Copyright © 2012, Elsevier Inc. All rights reserved. 69

Figure 4. 18 GPU Memory structures. GPU Memory is shared by all Grids (vectorized loops), Local Memory is shared by all threads of SIMD instructions within a thread block (body of a vectorized loop), and Private Memory is private to a single CUDA Thread. Copyright © 2011, Elsevier Inc. All rights Reserved. 70

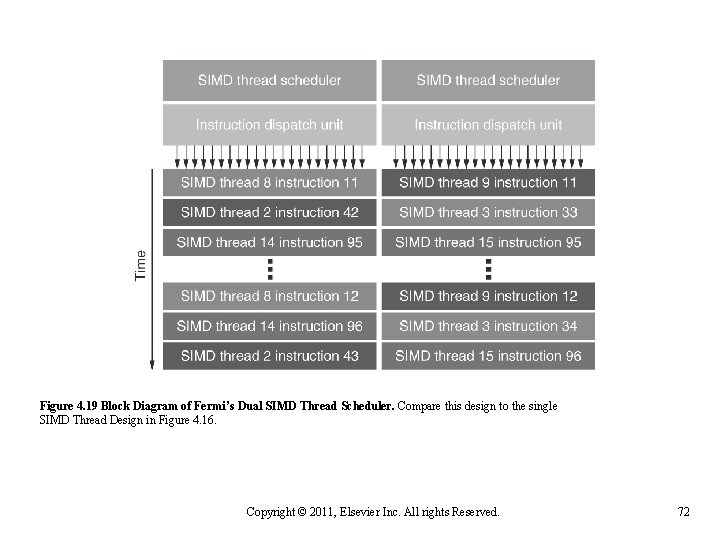
n Each SIMD processor has n n n n n Two SIMD thread schedulers, two instruction dispatch units 16 SIMD lanes (SIMD width=32, chime=2 cycles), 16 load-store units, 4 special function units Thus, two threads of SIMD instructions are scheduled every two clock cycles Graphical Processing Units Fermi Architecture Innovations Fast double precision: gen- 78 515 GFLOPs for DAXPY Caches for GPU memory: I/D L 1/SIMD proc and shared L 2 64 -bit addressing and unified address space: C/C++ ptrs Error correcting codes: dependability for long-running apps Faster context switching: hardware support, 10 X faster Faster atomic instructions: 5 -20 X faster than gen. Copyright © 2012, Elsevier Inc. All rights reserved. 71

Figure 4. 19 Block Diagram of Fermi’s Dual SIMD Thread Scheduler. Compare this design to the single SIMD Thread Design in Figure 4. 16. Copyright © 2011, Elsevier Inc. All rights Reserved. 72

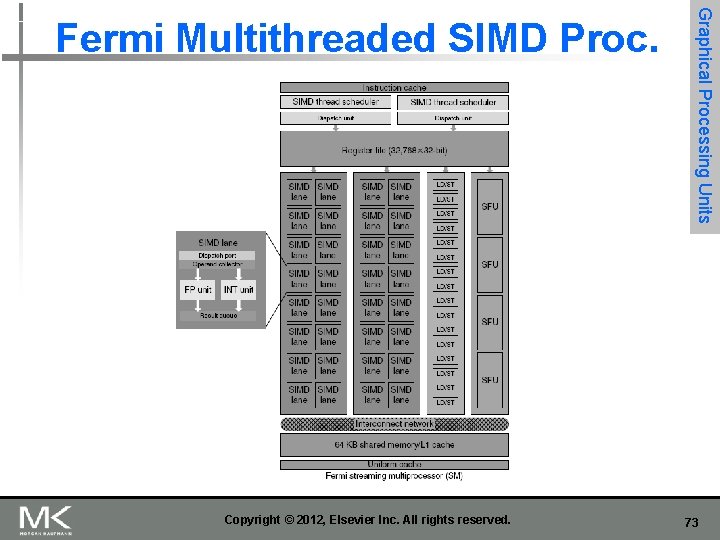
Copyright © 2012, Elsevier Inc. All rights reserved. Graphical Processing Units Fermi Multithreaded SIMD Proc. 73

n Focuses on determining whether data accesses in later iterations are dependent on data values produced in earlier iterations n n Loop-carried dependence Example 1: for (i=999; i>=0; i=i-1) x[i] = x[i] + s; n Detecting and Enhancing Loop-Level Parallelism Loop Level Parallelism No loop-carried dependence Copyright © 2012, Elsevier Inc. All rights reserved. 74

n Example 2: for (i=0; i<100; i=i+1) { A[i+1] = A[i] + C[i]; /* S 1 */ B[i+1] = B[i] + A[i+1]; /* S 2 */ } n n S 1 and S 2 use values computed by S 1 in previous iteration S 2 uses value computed by S 1 in same iteration Copyright © 2012, Elsevier Inc. All rights reserved. Detecting and Enhancing Loop-Level Parallelism Loop Level Parallelism 75

n n n Example 3: for (i=0; i<100; i=i+1) { A[i] = A[i] + B[i]; /* S 1 */ B[i+1] = C[i] + D[i]; /* S 2 */ } S 1 uses value computed by S 2 in previous iteration but dependence is not circular so loop is parallel Transform to: A[0] = A[0] + B[0]; for (i=0; i<99; i=i+1) { B[i+1] = C[i] + D[i]; A[i+1] = A[i+1] + B[i+1]; } B[100] = C[99] + D[99]; Copyright © 2012, Elsevier Inc. All rights reserved. Detecting and Enhancing Loop-Level Parallelism Loop Level Parallelism 76

n Example 4: for (i=0; i<100; i=i+1) { A[i] = B[i] + C[i]; D[i] = A[i] * E[i]; } n n No loop-carried dependence Example 5: for (i=1; i<100; i=i+1) { Y[i] = Y[i-1] + Y[i]; } n Detecting and Enhancing Loop-Level Parallelism Loop-carried dependence in the form of recurrence Copyright © 2012, Elsevier Inc. All rights reserved. 77

Detecting and Enhancing Loop-Level Parallelism Finding dependencies n Assume that a 1 -D array index i is affine: n n n a x i + b (with constants a and b) An index in an n-D array index is affine if it is affine in each dimension Assume: n n Store to a x i + b, then Load from c x i + d i runs from m to n Dependence exists if: n n Given j, k such that m ≤ j ≤ n, m ≤ k ≤ n Store to a x j + b, load from a x k + d, and a x j + b = c x k + d Copyright © 2012, Elsevier Inc. All rights reserved. 78

n n Generally cannot determine at compile time Test for absence of a dependence: n GCD test: n n If a dependency exists, GCD(c, a) must evenly divide (d-b) Example: for (i=0; i<100; i=i+1) { X[2*i+3] = X[2*i] * 5. 0; } n Detecting and Enhancing Loop-Level Parallelism Finding dependencies Answer: a=2, b=3, c=2, d=0 GCD(c, a)=2, d-b=3 no dependence possible. Copyright © 2012, Elsevier Inc. All rights reserved. 79

n Example 2: for (i=0; i<100; i=i+1) { Y[i] = X[i] / c; /* S 1 */ X[i] = X[i] + c; /* S 2 */ Z[i] = Y[i] + c; /* S 3 */ Y[i] = c - Y[i]; /* S 4 */ } n Watch for antidependencies and output dependencies: n n n RAW: S 1 S 3, S 1 S 4 on Y[i], not loop-carried WAR: S 1 S 2 on X[i]; S 3 S 4 on Y[i] WAW: S 1 S 4 on Y[i] Copyright © 2012, Elsevier Inc. All rights reserved. Detecting and Enhancing Loop-Level Parallelism Finding dependencies 80

n n Reduction Operation: for (i=9999; i>=0; i=i-1) sum = sum + x[i] * y[i]; Transform to… for (i=9999; i>=0; i=i-1) sum [i] = x[i] * y[i]; for (i=9999; i>=0; i=i-1) finalsum = finalsum + sum[i]; Do on p processors: for (i=999; i>=0; i=i-1) finalsum[p] = finalsum[p] + sum[i+1000*p]; Note: assumes associativity! Copyright © 2012, Elsevier Inc. All rights reserved. Detecting and Enhancing Loop-Level Parallelism Reductions 81