Database Management System Lecture 14 Logical Database Design

Database Management System Lecture - 14

Logical Database Design

Introduction to Relational Data Model

Two Major Strengths ØSimplicity ØStrong Mathematical Foundation

Relational Data Model ØPresented by E. F. Codd in 1970, then of IBM ØBefore Relational Data Model, two older data models were in use; Hierarchical, Network

Relational Data Model ØFirst DBMS built on Relational Data Model (RDM) was system R ØAnother Relational DBMS built during those days was INGRES

Basic of RDM ØRDM used mainly for external, conceptual, and to some extent physical schema ØSeparation of conceptual and physical levels makes manipulation much easier, contrary to previous data models

Basic of RDM ØRDM used for external, conceptual, and to some extent physical schema ØThe basic structure is relation ØBoth entities and relationships are modeled using tables/relations

Basics of RDM ØRelations physically represented as tables ØTable is a two dimensional representation of a relation ØConsists of rows and columns

Basics of RDM ØColumns represent attributes and rows represent records ØRows, records and tuples all these terms are used interchangeably

Basic Properties of a Table 1. Each cell of a table contains atomic/single value 2. Each column has a distinct name; the name of the attribute it represents

Basic Properties of a Table 3. The values of the attributes come from the same domain 4. The order of the columns is immaterial

Basic Properties of a Table 5. The order of the rows is immaterial 6. Each row/tuple/record is distinct, no two rows can be same

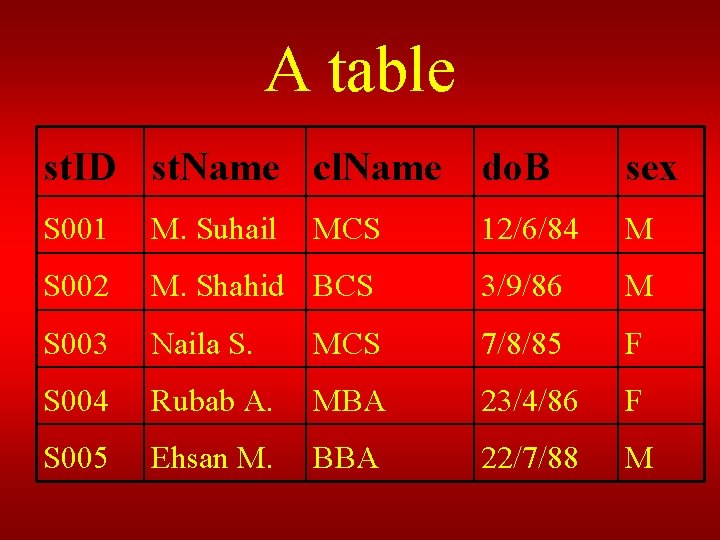
A table st. ID st. Name cl. Name do. B sex S 001 M. Suhail 12/6/84 M S 002 M. Shahid BCS 3/9/86 M S 003 Naila S. MCS 7/8/85 F S 004 Rubab A. MBA 23/4/86 F S 005 Ehsan M. BBA 22/7/88 M MCS

Components of RDM Ø As discussed in data model definition 1. Structure (relation/table) 2. Manipulation language (SQL) 3. Integrity constraints (Two)

Mathematical Relations ØConsider two sets Ø A = {x, y} B = {2, 4, 6} Ø Cartesian product of these sets Ø A X B= {(x, 2), (x, 4), (x, 6), (y, 2), (y, 4), (y, 6)}

Mathematical Relations ØA relation is some subset of this Cartesian product, For example, Ø R 1= {(x, 2), (y, 2), (x, 6), (x, 4)} Ø R 2 = {(x, 4), (y, 6), (y, 4)}

Mathematical Relations The same notion of Cartesian product and relations can be applied to more than two sets, e. g. in case of three sets, we will have a relation of ordered triplets

Database Relations ØThinking in some real world scenario § Name = {Ali, Sana, Ahmed, Sara} § Age = {15, 16, 17, 18, ……. , 25}

Database Relations Cartesian product of Name & Age Name X Age= {(Ali, 15), (Sana, 15), (Ahmed, 15), (Sara, 15), …. , (Ahmed, 25), (Sara, 25)} CLASS = {(Ali, 18), (Sana, 17), (Ali, 20), (Ahmed, 19)}

Database Relations ØLet A 1, A 2, A 3, …, An be some attributes and D 1, D 2, D 3, …, Dn be their domains ØA relation scheme relates certain attributes with their domain in context of a relation

Relation Scheme Can be represented as R = (A 1: D 1, A 2: D 2, ……, An: Dn) STD = (st. Id: Text, st. Name: text, st. Adres: Text, do. B: Date) OR STD(st. Id, st. Name, st. Adres, do. B)

Database Relations According to this scheme we can have a relation (instance of this scheme), like STD={(st. Id: S 001, st. Name: Ali, st. Adres: Lahore, do. B: 12/12/76), (st. Id: S 003, st. Name: A. Rehman, st. Adres: RWP, do. B: 2/12/77)}

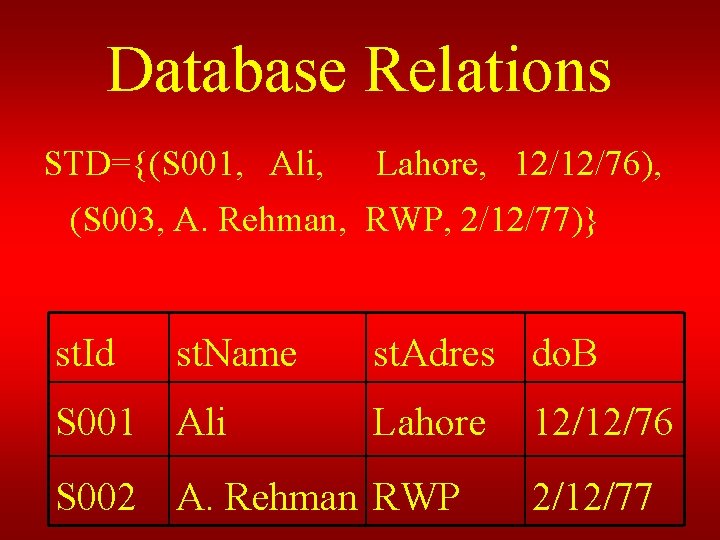
Database Relations STD={(S 001, Ali, Lahore, 12/12/76), (S 003, A. Rehman, RWP, 2/12/77)} st. Id st. Name S 001 Ali st. Adres do. B Lahore S 002 A. Rehman RWP 12/12/76 2/12/77