Database Functional Dependencies Designing Good Schemas l We

Database Functional Dependencies

Designing Good Schemas l We know how to create schemas, but. . . l l l how do we create good schemas? what does good mean? Schema quality measurements: l l l semantics of the attributes minimal redundancy minimal frequency of null values

Functional Dependences l A column Y of relational table R is functionally dependent up on column X of relational table R if and only if: Each value of X in R associated with each value of Y at any given time

Functional Dependencies Definition: A 1, . . . , Am B 1, . . . , Bn holds in R if: t, t’ R, (t. A 1=t’. A 1 . . . t. Am=t’. Am t. B 1=t’. B 1 . . . t. Bm=t’. Bm ) R A 1 . . . Am B 1 . . . Bm t t’ if t, t’ agree here then t, t’ agree here

Examples Emp. ID E 0045 E 1847 E 1111 E 9999 l l l Name Smith John Smith Mary Phone 1234 9876 1234 Position Clerk Salesrep Lawyer Emp. ID Name, Phone, Position Phone but Phone Position

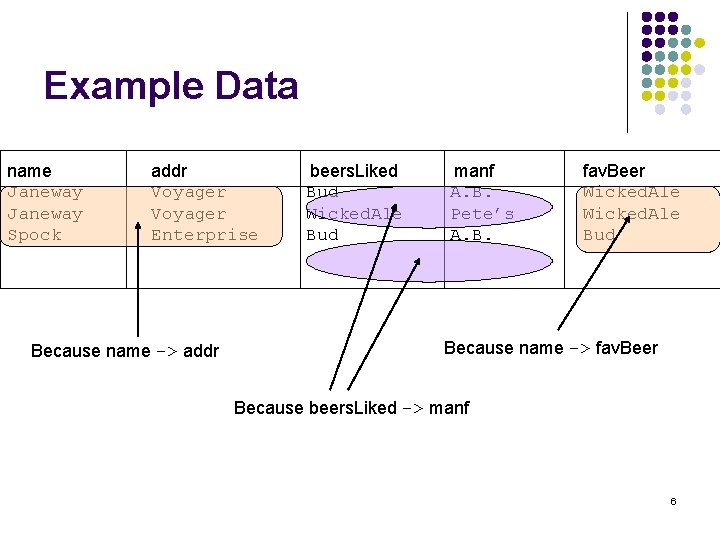
Example Data name Janeway Spock addr Voyager Enterprise Because name -> addr beers. Liked Bud Wicked. Ale Bud manf A. B. Pete’s A. B. fav. Beer Wicked. Ale Bud Because name -> fav. Beer Because beers. Liked -> manf 6

Example Drinkers(name, addr, beers. Liked, manf, favorite. Beer) l Reasonable FD's to assert: 1. name addr 2. name favorite. Beer 3. beers. Liked manf

Functional dependences l l Y is functional dependent up on X same as values of X identify values of Y If X Y then XZ YZ IF X Y and Y Z then X Z X Y means that Y depend on X or X identify Y

Examples l l l S# Ename {S#, P#} Hours If for each value of S#, there are exactly one corresponding value for sname, state, city then: S# Sname Sate City

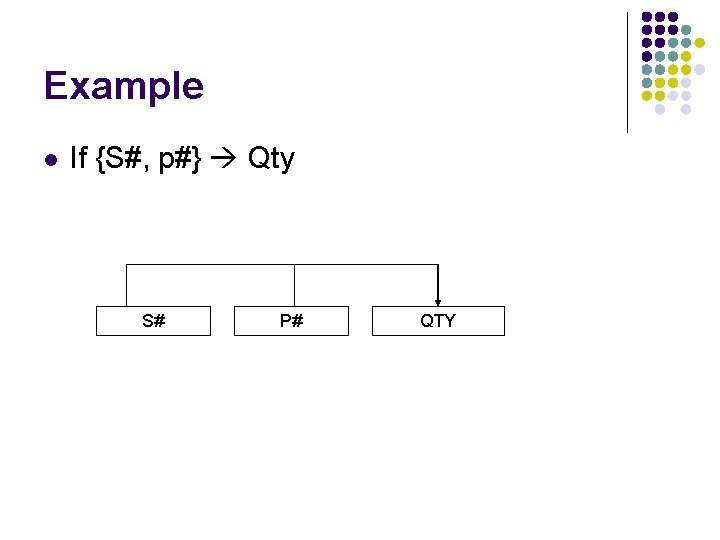
Example l If {S#, p#} Qty S# P# QTY

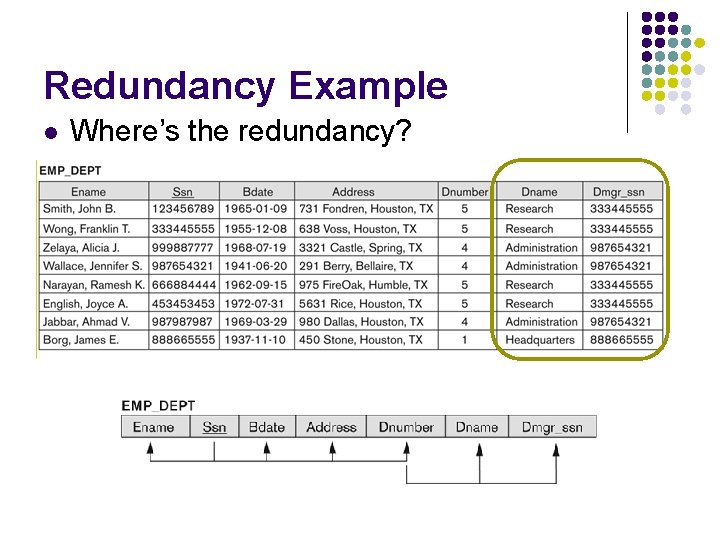
Redundancy Example l Where’s the redundancy?

Redundancy Example

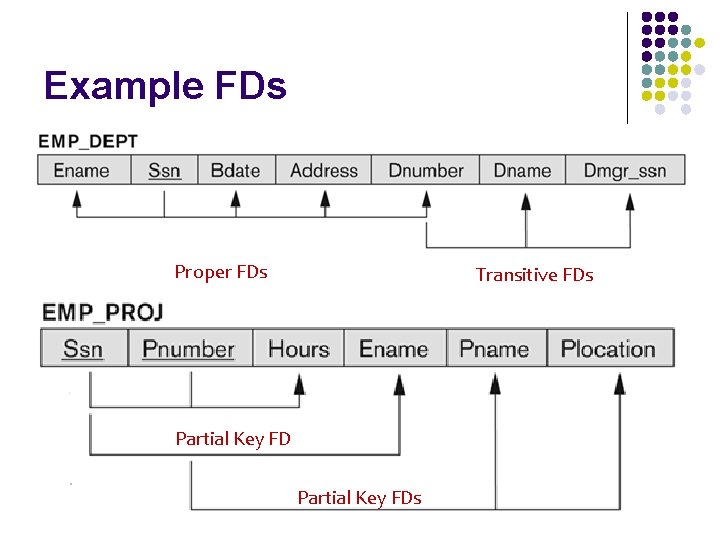
Example FDs Proper FDs Transitive FDs Partial Key FDs

Example l l R = (A, B, C, G, H, I) F = { A B A C CG H CG I B H} some members of F+ l A H l l AG I l l by transitivity from A B and B H by augmenting A C with G, to get AG CG and then transitivity with CG I CG HI by augmenting CG I to infer CG CGI, and augmenting of CG H to infer CGI HI, and then transitivity l

Formal definition of a key l A key is a set of attributes A 1, . . . , An s. t. for any other attribute B, A 1, . . . , An B l A minimal key is a set of attributes which is a key and for which no subset is a key l Note: book calls them superkey and key

Where Do Keys Come From? 1. 2. We could simply assert a key K. Then the only FD’s are K -> A for all atributes A, and K turns out to be the only key obtainable from the FD’s. We could assert FD’s and deduce the keys by systematic exploration. u E/R gives us FD’s from entity-set keys and many-one relationships. 16

Examples of Keys l Product(name, price, category, color) name, category price category color Keys are: {name, category} and all supersets l Enrollment(student, address, course, room, time) student address room, time course student, course room, time Keys are: [in class]

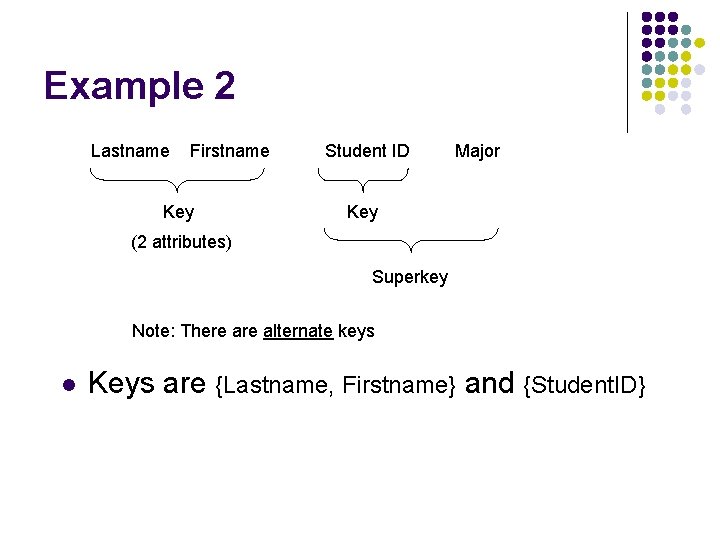
Example 2 Lastname Firstname Student ID Major Key (2 attributes) Superkey Note: There alternate keys l Keys are {Lastname, Firstname} and {Student. ID}

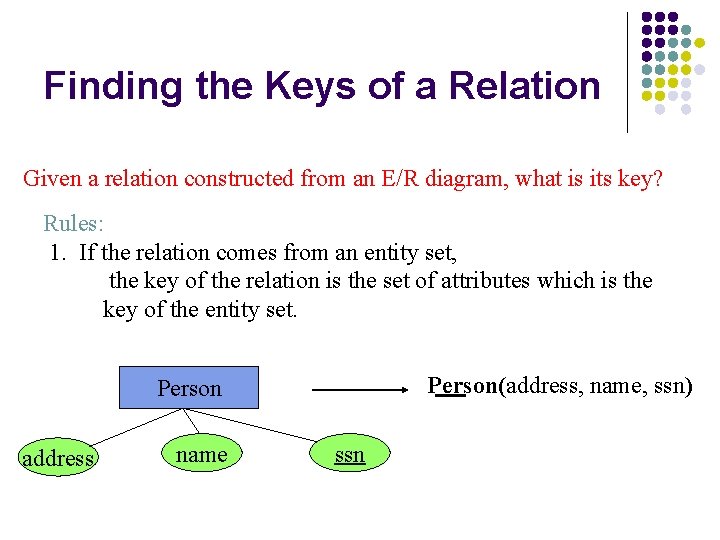
Finding the Keys of a Relation Given a relation constructed from an E/R diagram, what is its key? Rules: 1. If the relation comes from an entity set, the key of the relation is the set of attributes which is the key of the entity set. Person(address, name, ssn) Person address name ssn

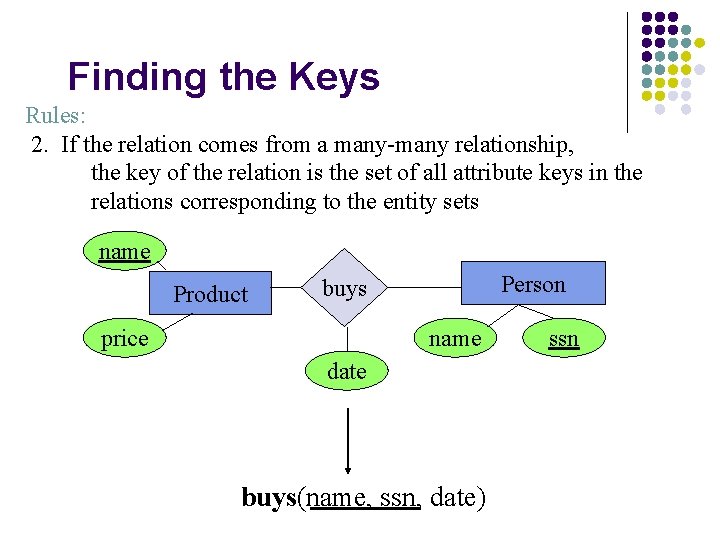
Finding the Keys Rules: 2. If the relation comes from a many-many relationship, the key of the relation is the set of all attribute keys in the relations corresponding to the entity sets name Product Person buys price name date buys(name, ssn, date) ssn

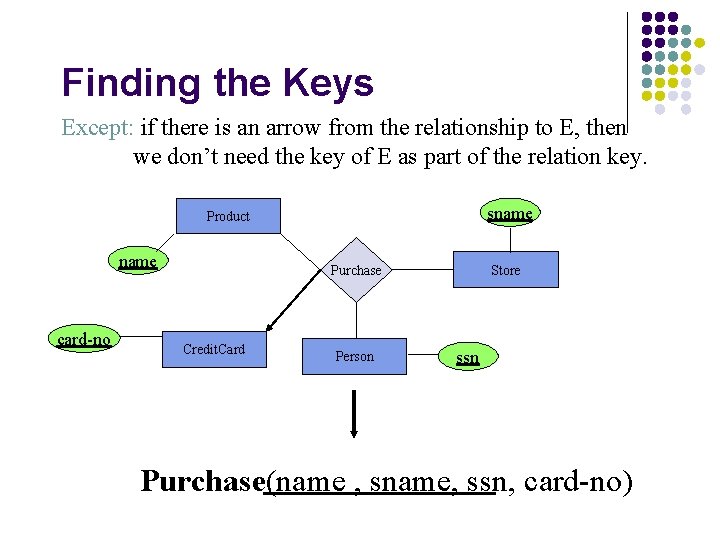
Finding the Keys Except: if there is an arrow from the relationship to E, then we don’t need the key of E as part of the relation key. sname Product name card-no Purchase Credit. Card Person Store ssn Purchase(name , sname, ssn, card-no)

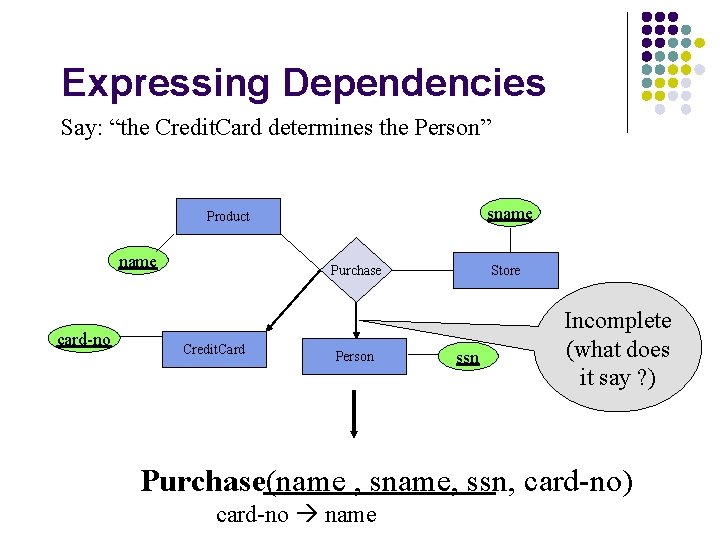
Expressing Dependencies Say: “the Credit. Card determines the Person” sname Product name card-no Purchase Credit. Card Person Store ssn Incomplete (what does it say ? ) Purchase(name , sname, ssn, card-no) card-no name

l Enrollment(student, major, course, room, time) student major, course room course time What else can we infer ?

Relational Schema Design (or Logical Design) Main idea: l Start with some relational schema l Find out its FD’s l l Important also to look at inferred FD’s. Use them to design a better relational schema

Relational Schema Design Recall set attributes (persons with several phones): Name SSN Phone. Number City Fred 123 -45 -6789 206 -555 -1234 Seattle Fred 123 -45 -6789 206 -555 -6543 Seattle Joe 987 -65 -4321 908 -555 -2121 Westfield Joe 987 -65 -4321 908 -555 -1234 Westfield SSN Name, City, but not SSN Phone. Number Anomalies: Redundancy = repeat data • Update anomalies = Fred moves to “Bellvue” • Deletion anomalies = Fred drops all phone numbers: • what is his city ?

Relation Decomposition Break the relation into two: Name SSN City Fred 123 -45 -6789 Seattle Joe 987 -65 -4321 Westfield SSN Phone. Number 123 -45 -6789 206 -555 -1234 123 -45 -6789 206 -555 -6543 987 -65 -4321 908 -555 -2121 987 -65 -4321 908 -555 -1234

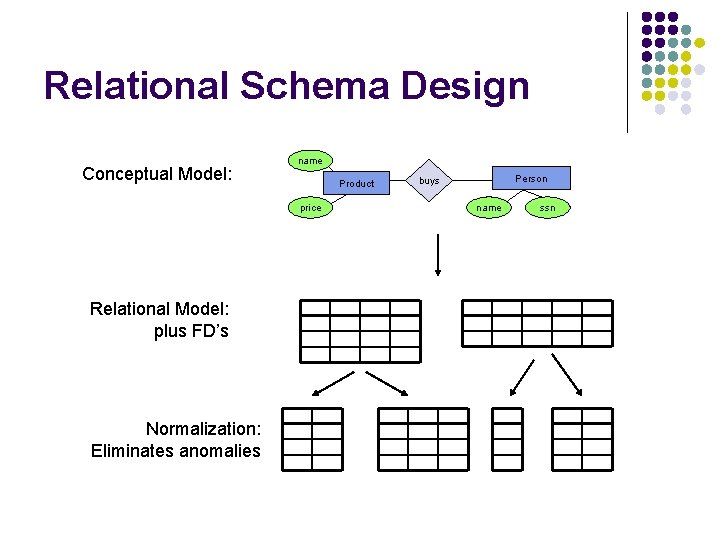
Relational Schema Design Conceptual Model: name Product price Relational Model: plus FD’s Normalization: Eliminates anomalies Person buys name ssn

Decompositions in General R(A 1, . . . , An) Create two relations R 1(B 1, . . . , Bm) and R 2(C 1, . . . , Cp) such that: B 1, . . . , Bm C 1, . . . , Cp = A 1, . . . , An and: R 1 = projection of R on B 1, . . . , Bm R 2 = projection of R on C 1, . . . , Cp

Incorrect Decomposition l Sometimes it is incorrect: Name Price Category Gizmo 19. 99 Gadget One. Click 24. 99 Camera Double. Click 29. 99 Camera Decompose on : Name, Category and Price, Category

Incorrect Decomposition Name Category Price Category Gizmo Gadget 19. 99 Gadget One. Click Camera 24. 99 Camera Double. Click Camera 29. 99 Camera When we put it back: Cannot recover information Name Price Category Gizmo 19. 99 Gadget One. Click 24. 99 Camera One. Click 29. 99 Camera Double. Click 24. 99 Camera Double. Click 29. 99 Camera

Normal Forms l l Each normal form is a set of conditions on a schema that guarantees certain properties (relating to redundancy and update anomalies( The two commonly used normal forms are third normal form (3 NF) and Boyce-Codd normal form (BCNF( 31

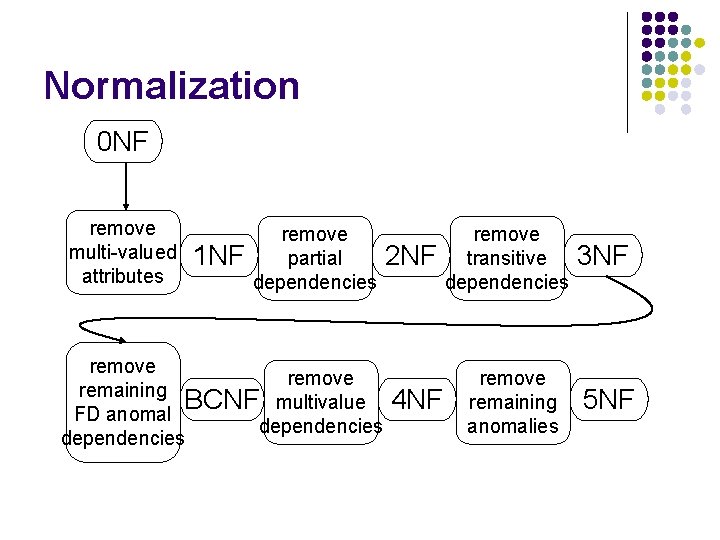
Normalization 0 NF remove multi-valued attributes 1 NF remove partial dependencies remove remaining BCNF multivalue FD anomal dependencies 2 NF 4 NF remove transitive dependencies remove remaining anomalies 3 NF 5 NF

Goals of Normalization l l l Let R be a relation scheme with a set F of functional dependencies. Decide whether a relation scheme R is in “good” form. In the case that a relation scheme R is not in “good” form, decompose it into a set of relation scheme {R 1, R 2, . . . , Rn} such that l l l each relation scheme is in good form the decomposition is a lossless-join decomposition Preferably, the decomposition should be dependency preserving.

1 NF l First normal form is l NO multi-valued attributes l No composite attribute l No nested relation We create new table or new field (telephone, visiting)

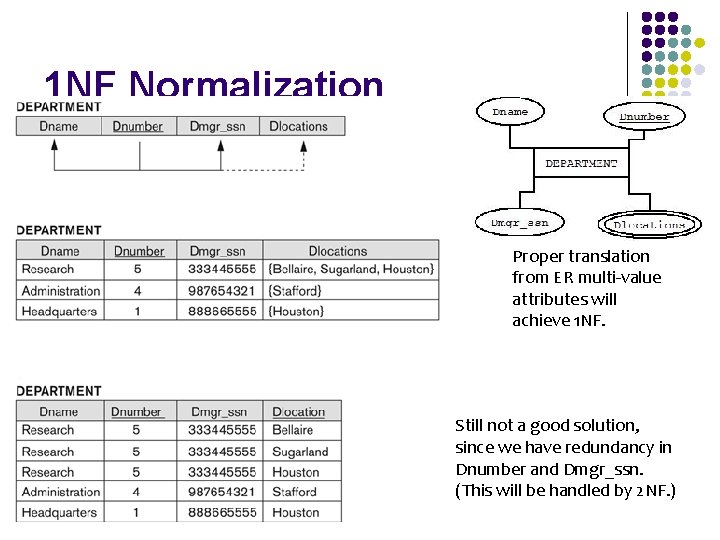
1 NF Normalization Proper translation from ER multi-value attributes will achieve 1 NF. Still not a good solution, since we have redundancy in Dnumber and Dmgr_ssn. (This will be handled by 2 NF. )

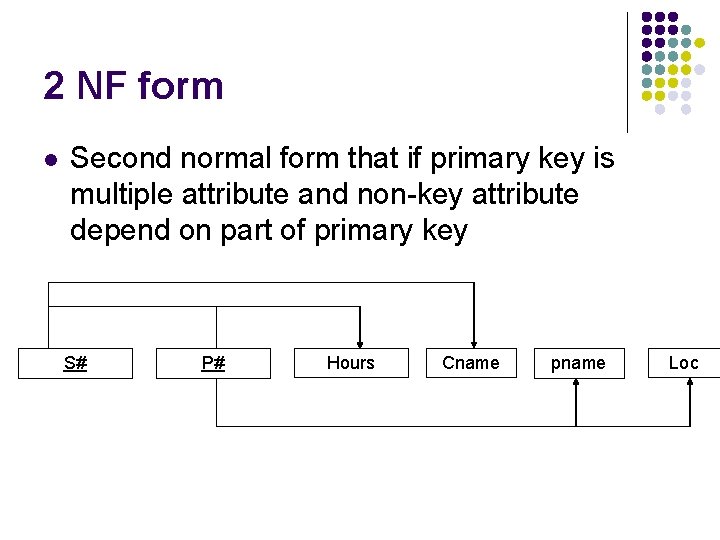
2 NF form l Second normal form that if primary key is multiple attribute and non-key attribute depend on part of primary key S# P# Hours Cname pname Loc

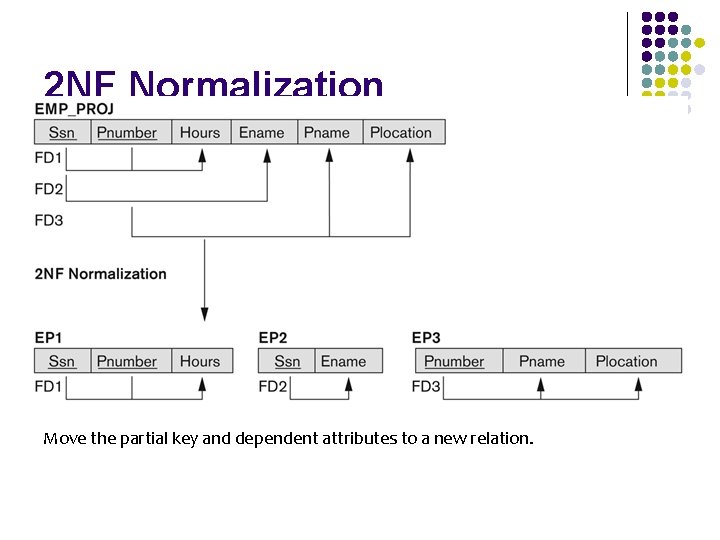
2 NF Normalization Move the partial key and dependent attributes to a new relation.

Transitive Dependencies l l X → Y is a transitive dependency (PD) if there exists Z ⊈ any key such that X → Z → Y TDs can cause redundancy if there are multiple values of X that determine the same value of Z l l the value of Y for that value of Z is stored multiple times 3 NF normalization: move (Z, Y) to new relation in which Z is the primary key

3 NF l The relation in 3 NF if it is 2 NF and every non -key attribute is non-transitively dependent on primary key

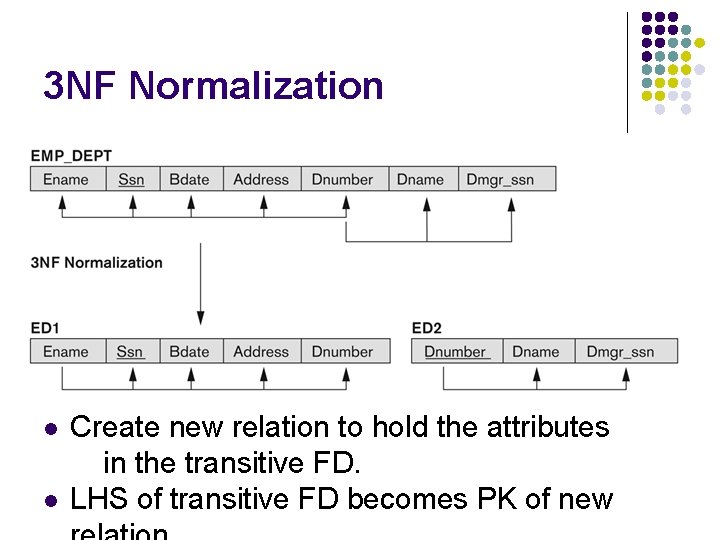
3 NF Normalization l l Create new relation to hold the attributes in the transitive FD. LHS of transitive FD becomes PK of new

Transitive Dependency Example DEPT COURSE SECTION ROOM INSTR I_OFFICE (instructor's office) is determined by the non-PK attribute INSTR DEPT COMP COMP COURSE 51 51 163 53 53 SECTION 1 2 1 1 2 ROOM WPC 122 WPC 219 WPC 122 WPC 130 INSTR I_OFFICE DOHERTY CSB 109 CLIBURN CSB 107 DOHERTY CSB 109 BOWRING CSB 108 CARMAN CSB 104

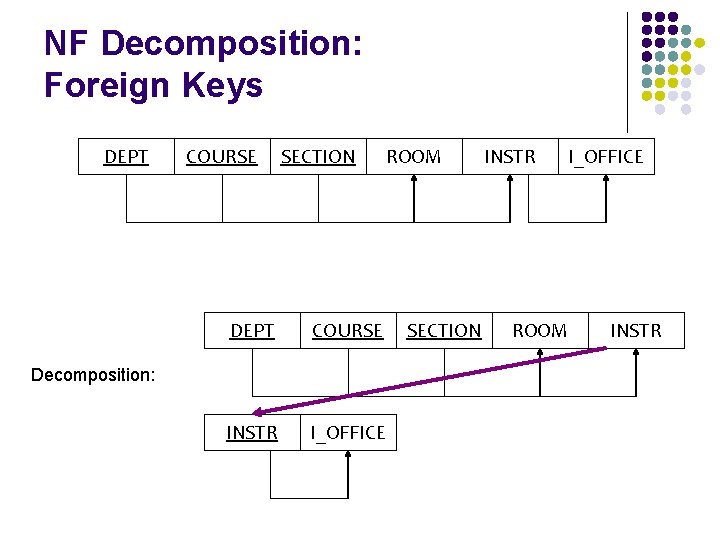
NF Decomposition: Foreign Keys DEPT COURSE SECTION ROOM DEPT COURSE INSTR I_OFFICE Decomposition: SECTION INSTR I_OFFICE ROOM INSTR

3 NF Example l Relation dept_advisor: l l l dept_advisor (s_ID, i_ID, dept_name) F = {s_ID, dept_name i_ID, i_ID dept_name} Two candidate keys: s_ID, dept_name, and i_ID, s_ID R is in 3 NF l s_ID, dept_name i_ID s_ID § l dept_name is a superkey i_ID dept_name § dept_name is contained in a candidate key

Redundancy in 3 NF l l There is some redundancy in this schema Example of problems due to redundancy in J L K 3 NF l R = (J, K, L) F = {JK L, L K } j 1 l 1 k 1 j 2 l 1 k 1 j 3 l 1 k 1 null l 2 k 2 n repetition of information (e. g. , the relationship l 1, k 1) l (i_ID, dept_name) n need to use null values (e. g. , to represent the relationship l 2, k 2 where there is no corresponding value for J). l (i_ID, dept_name. I) if there is no separate relation mapping instructors to departments

3 NF Decomposition: An Example l Relation schema: cust_banker_branch = (customer_id, employee_id, branch_name, type ) l The functional dependencies for this relation schema are: 1. 2. 3. l customer_id, employee_id branch_name, type employee_id branch_name customer_id, branch_name employee_id We first compute a canonical cover l l branch_name is extraneous in the r. h. s. of the 1 st dependency No other attribute is extraneous, so we get FC = customer_id, employee_id type employee_id branch_name customer_id, branch_name employee_id

Normalization Goal = BCNF = Boyce-Codd Normal Form = all FD’s follow from the fact “key everything. ” l Formally, R is in BCNF if for every nontrivial FD for R, say X A, then X is a superkey. l “Nontrivial” = right-side attribute not in left side. Why? 1. Guarantees no redundancy due to FD’s. 2. Guarantees no update anomalies = one occurrence of a fact is updated, not all. 3. Guarantees no deletion anomalies = valid fact is lost when tuple is deleted.

Boyce-Codd Normal Form A relation schema R is in BCNF with respect to a set F of functional dependencies if for all functional dependencies in F+ of the form where R and R, at least one of the following holds: l l is trivial (i. e. , ) is a superkey for R Example schema not in BCNF: instr_dept (ID, name, salary, dept_name, building, budget ) because dept_name building, budget holds on instr_dept, but dept_name is not a superkey

Third Normal Form l A relation schema R is in third normal form (3 NF) if for all: in F+ at least one of the following holds: is trivial (i. e. , ) l is a superkey for R l Each attribute A in – is contained in a candidate key for R. (NOTE: each attribute may be in a different candidate key) l l l If a relation is in BCNF it is in 3 NF (since in BCNF one of the first two conditions above must hold). Third condition is a minimal relaxation of BCNF to ensure dependency preservation (will see why later).

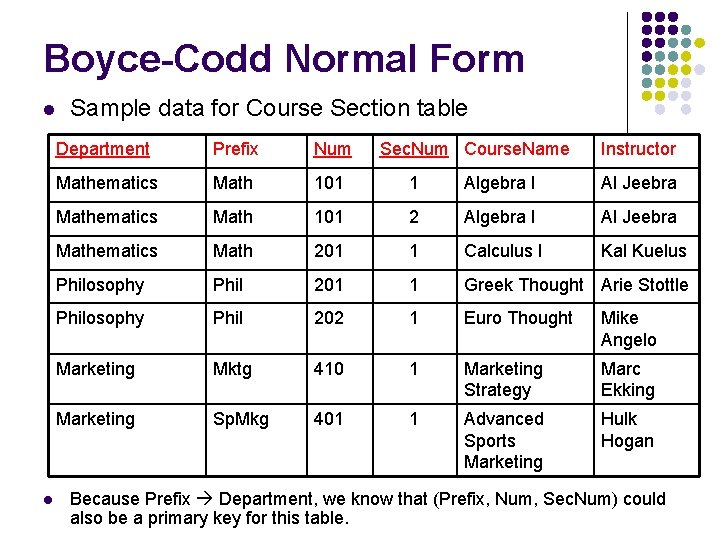
Boyce-Codd Normal Form l l Sample data for Course Section table Department Prefix Num Sec. Num Course. Name Instructor Mathematics Math 101 1 Algebra I Al Jeebra Mathematics Math 101 2 Algebra I Al Jeebra Mathematics Math 201 1 Calculus I Kal Kuelus Philosophy Phil 201 1 Greek Thought Arie Stottle Philosophy Phil 202 1 Euro Thought Mike Angelo Marketing Mktg 410 1 Marketing Strategy Marc Ekking Marketing Sp. Mkg 401 1 Advanced Sports Marketing Hulk Hogan Because Prefix Department, we know that (Prefix, Num, Sec. Num) could also be a primary key for this table.

Example Students(name, addr, phones, Car. Liked) l A student’s phones are independent of the cars they like. l Thus, each of a student’s phones appears with each of the cars they like in all combinations. l This repetition is unlike redundancy due to FD’s, of which name->addr is the only one. 50

Example l l l Students(name, addr, Car. Liked, manf, fav. Car) FD’s: name->addr fav. Car, cars. Liked->manf Only key is {name, Cars. Liked}. In each FD, the left side is not a superkey. Any one of these FD’s shows Students is not in BCNF 51

Boyce-Codd Normal Form l We say a relation R is in BCNF if whenever X ->A is a nontrivial FD that holds in R, X is a superkey. l l Remember: nontrivial means A is not a member of set X. Remember, a superkey is any superset of a key (not necessarily a proper superset). 52

Example l l l Students(name, addr, Cars. Liked, manf, fav. Car) F = name->addr, name -> fav. Car, Cars. Liked->manf Pick BCNF violation name->addr. Close the left side: {name}+ = {name, addr, fav. Car}. Decomposed relations: 1. Students 1(name, addr, fav. Car) 2. Students 2(name, Cars. Liked, manf) 53

3 NF and BCNF l l 3 rd Normal Form (3 NF) modifies the BCNF condition so we do not have to decompose in this problem situation. X ->A violates 3 NF if and only if X is not a superkey, and also A is not prime. 54

Exercises The following relation schema is not in third normal form (3 NF). l SHIPMENT SID FROM_CITY TO_CITY DISTANCE WEIGHT Is this an example of a transitive dependency or a partial key dependency? Give an equivalent schema that is in 3 NF.

Exercises l This relation has been proposed to track Pacific alumni: Alumni( SID, Last. Name, First. Name, Degree, Year. Awarded, Phone). Pacific allows students to receive multiple degrees, possibly in different years. Identify all FDs. Give a new schema that is in third normal form.

Exercises l Consider the following relation schema: Movie(title, genre, length, actor, sag_id, studio_addr) l l l Every movie has a unique title. A movie may have multiple actors. Each actor has a unique sag_id. An actor may appear in multiple movies. A movie has exactly one studio, but a studio may produce more than one movie. Each studio has exactly one address. l Identify all functional dependencies. l Normalize the schema to 3 NF.

INDEX l Is used to speed up the retrieval of records in response to certain search conditions l Any field of the file can be used to create an index

Index l Multiple indexes on different fields can be constructed on same file. l Is specified on the ordered key field of file (single index) and B+ tree (multiple indexes)

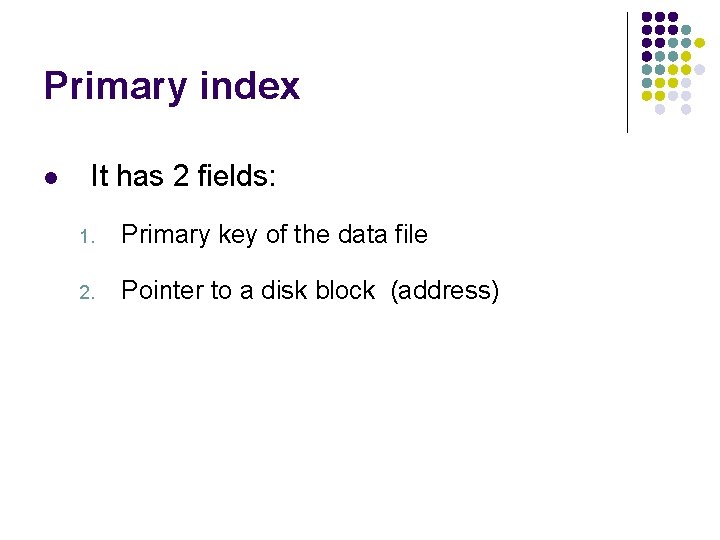
Primary index l It has 2 fields: 1. Primary key of the data file 2. Pointer to a disk block (address)

Index problem l The main problem with primary index is insertion and deletion of records l To insert a record in its correct position, other records be shifted to give space for new one.

Clustering index l It based on a non-key field in the file where the record value can be repeated so it clustering into groups l The record insertion and deletion still cause a problem

Clustering index l The primary index requires a distinct value for each record l In clustering index, there is one entry for each distinct value

Secondary index l It based on some non-ordering field of the data file. l There can be many secondary indexes for same file

Example l Create a database for managing class enrollments in a single semester. You should keep track of all students (their names, Ids, and addresses) and professors (name, Id, department). Do not record the address of professors but keep track of their ages. Maintain records of courses also. Like what classroom is assigned to a course, what is the current enrollment, and which department offers it. At most one professor teaches each course. Each student evaluates the professor teaching the course. Note that all course offerings in the semester are unique, i. e. course names and numbers do not overlap. A course can have ≥ 0 pre-requisites, excluding itself. A student enrolled in a course must have enrolled in all its pre-requisites. Each student receives a grade in each course. The departments are also unique, and can have at most one chairperson (or dept. head). A chairperson is not allowed to head two or more departments.