Database Design Theory www assignmentpoint com Database Design

Database Design Theory www. assignmentpoint. com

Database Design Theory n Given some body of data to be represented in a database, as modelled in an E-R diagram, what is the most suitable logical structure for that data? n How do we decide on the appropriate tables and the attributes of the tables? www. assignmentpoint. com

Requirements n Accommodate data integrity. n General integrity constraints n n E. g. , referential integrity Domain specific integrity constraints n E. g. , no user can borrow more than 4 books. n Robust in the sense that the design should be application independent. n We try to achieve this through the elimination of redundancy. www. assignmentpoint. com

The Danger of Redundancy n Consider the example n For students, we want to know student ID, name and address. n For courses, we need to know course ID, title and lecturer. n For employees, we need to know the employee ID, name and department. n For each department, we need to know the department ID, the name and the location. n For each enrollment, we need to know the grade. www. assignmentpoint. com

The Danger of Redundancy Continued n One solution store everything in one big table Appl(sid, name, addr, cid, title, eid, ename, dept. ID, dname, loc, grade) n Clearly, this leads to redundancy. n For example, we need to store the student’s address for every course they have been registered for. www. assignmentpoint. com

The Danger of Redundancy. Conclusion n If everything in one table, then n Greater space requirements n Insertion anomalies n n Deletion anomalies n n Cannot store information on student who has not passed a course yet. We may want to delete a course but some student may be registered only for that course. Update anomalies n n If a student changes their address, many tuples need to be updated. www. assignmentpoint. com Danger of inconsistency in database.

Good Database Design n The basic idea: n A “good” database is one in which each table consists of a primary key and a set of mutually independent attributes. n Strategy for achieving a good database design: n Identify undesirable dependencies in a table and decompose by projection. www. assignmentpoint. com

Functional Dependencies (FD’s) n Attribute (set) Y is functionally dependent on attribute (set) X if, whenever two tuples have the same value for X, they also have the same value for Y. n Notation: X Y n X is called the determinant. n An FD A B is non-trivial if and only if B A and B A. www. assignmentpoint. com

Functional Dependencies in Our Example. n If everything is in one table, then these FD’s exist: n sid name, addr n cid title n eid ename n deptid dname, loc n sid, cid grade n Note we also have n sid, cid, eid, deptid All other attributes www. assignmentpoint. com

Keys Again n A set of attributes X in a relation R is a superkey if every attribute in R is functionally dependent on X. n A candidate key is a minimal superkey. n Alternate keys are candidate keys that have not been selected as primary keys. n A prime attribute is a member of a candidate key. www. assignmentpoint. com

Armstrong’s Axioms n Let X, Y and Z be sets of attributes of a relation R n Reflexivity: (X Y) (X Y) n Augmentation (X Y) (XZ YZ) n Transitivity ((X Y) & (Y Z)) (X Z) n Axioms are sound and complete n Can derive all FDs that follow from a given set of FDs. n Derive only true FDs www. assignmentpoint. com

Some Consequences of Armstrong’s Axioms n The following are implied by Armstrong’s axioms: n Decomposition (X YZ) (X Y) n Union ((X Y)&(X Z)) (X YZ) n Pseudo transitivity ((X Y)&(WY Z)) (WX Z) www. assignmentpoint. com

Closure of a Set of Functional Dependencies n If F is a set of functional dependencies, the closure of F, F+, is the set of all functional dependencies logically implied by those in F. n Useful since it allows us to determine candidate keys (there must be functional dependency to all other attributes), but very expensive to compute. www. assignmentpoint. com

Closure Under a Set of Functional Dependencies n Since F+ is too expensive to compute, we use closure of X under a set of functional dependencies, X+. n (X Y) in F if and only if Y X +. n Since X+ is relatively easy to compute, we can now verify whether X is a superkey. www. assignmentpoint. com

Computing X+. n To compute X+ under a set of FDs F: INPUT: X, F OUTPUT: X+ S : = X WHILE there is a (Z Y) in F with Z S and Y S DO S : = SY ENDWHILE X+ = S www. assignmentpoint. com

Decomposition n Recall that having identified undesirable FDs, we now need to decompose. n Decomposition: Let U be a relation scheme. A set of {R 1, . . , Rn} of relation schemes is a decomposition of U if R 1 … Rn = U n Every attribute of U occurs in at least one Ri. n www. assignmentpoint. com

Desirable Properties of Decomposition n Decompositions should be n Lossless n Dependency preserving n No redundancy n Minimal number of tables n Sometimes, not all properties can be achieved simultaneously. www. assignmentpoint. com

Lossless Decomposition n Let n {R 1, . . , Rn} a decomposition of U n u relation instance over U n Pi = Ri(u) for i from 1 to n n Then n {R 1, . . , Rn} is a lossless decomposition if u = P 1 … P n n In other words, the original relation can be reconstructed. www. assignmentpoint. com

Dependency Preserving Decompositions n In decomposing a table, ensure that any FDs are easily enforceable. n Example: Relation U(A, B, C) n FDs: A B, A C, B C n If we decompose U into R(A, B) and S(B, C), then A B, B C can be easily enforced when changing R or S. n Because of transitivity, A C is automatically enforced. n www. assignmentpoint. com

Non-Dependency Preserving Decomposition n If we decompose U into R’(A, B) and S’(A, C), then enforcing A B and A C is easy. n However, B C becomes an interrelational constraint and can only be enforced through a join. n This decomposition is not dependency preserving. www. assignmentpoint. com

Normalization n Normal forms, as defined in relational database theory, are guidelines for the design of the tables in the database. n Normalization reduces redundancy. n Important to remember why we want to avoid redundancy Space requirements n Insertion, deletion and update anomalies. n www. assignmentpoint. com

The Normal Forms n First normal form n Second normal form n Third normal form n Boyce-Codd normal form n Fourth normal form n Fifth normal form n The normal forms are ordered in that everything in 2 NF is also in 1 NF. n We ignore 5 NF, as violations hardly occur in practice. www. assignmentpoint. com

First Normal Form n A relation is in 1 NF iff the value of each attribute in a tuple is atomic. n A relation which is not in 1 NF sid 123 234 cid CS 51 S CS 51 T CS 51 S CS 52 T grade A B C B B www. assignmentpoint. com

Getting Tables into 1 NF n Normalizing a table which is not in 1 NF is easy: Simply repeat the other fields. n Thus sid 123 234 234 cid CS 51 S CS 51 T CS 51 S CS 52 T grade A B C B B www. assignmentpoint. com

Second and Third Normal Form n Second and third normal form concern relationship between non-key and prime attributes. n Recall that a prime attribute is a member of a candidate key. n Under 2 NF and 3 NF, a non-key attribute value must provide a fact about the key, the whole key and nothing but the key. n Every non-prime attribute must be fully functionally dependent on a candidate key. www. assignmentpoint. com

Second Normal Form n 2 NF is violated when a non-key attribute depends on a proper subset of a candidate key. n The following violates 2 NF Result(cid, sid, name, grade) n as name is functionally dependent on sid alone. www. assignmentpoint. com

Dangers of Violating 2 NF n Note that name is repeated for every course that a student has a grade for. n Problems: Danger of inconsistency if a student changes their name, e. g. , by getting married. n If a student has not passed any courses yet, then the student’s name cannot be stored. n www. assignmentpoint. com

Getting Tables into 2 NF n Decompose the table into Result(cid, sid, grade) Student(sid, name) n This decomposition leads to longer retrieval times for queries which involve joins. n Normalization is necessary to avoid anomalies which arise because of changes to attributes. n If little chance of changes, then sometimes do not normalize. www. assignmentpoint. com

Third Normal Form n Third normal form is violated when a non-prime attribute depends on another non-prime attribute. n The following violates 3 NF Empl(eid, dept, loc) n loc is a fact about dept. n Danger same as violation of 2 NF. www. assignmentpoint. com

Getting Tables into 3 NF n Again, decompose Empl(eid, dept) Department(dept, loc) n We can always restore 3 NF through a lossless and dependency preserving decomposition. www. assignmentpoint. com

Boyce-Codd Normal Form (BCNF) n A relation scheme R is in BCNF if every determinant of a FD over R is a candidate key. n In other words, the determinant of every FD is a superkey. n Violation of BCNF R(A, B, C, D, E, F) n { A BC, D AEF } n D+ = ABCDEF n n n D is a good primary key. A+ = ABC www. assignmentpoint. com

Another Violation of BCNF n Assume that we give each registration for a course a unique registration number Reg(rid, sid, cid, sname, grade) n FDs n rid sid, cid n sid, cid rid, grade n sid sname n rid+ = All attributes www. assignmentpoint. com

Getting Tables into BCNF n Decompose according to the FD whose determinant is not a superkey. n In our example, sid sname n This gives n n Reg(rid, sid, cid, grade) Stud(sid, sname) n Not always possible to get tables into BCNF while preserving all functional dependencies. www. assignmentpoint. com

Example where BCNF is not possible n Consider n R(A, B, C) n { AB C, C B} n Not in BCNF because C is not a superkey. n However, every decomposition of R fails to be dependency preserving as we have to split up the attributes in AB C n Have to settle for 3 NF. www. assignmentpoint. com

Multivalued Dependencies (MVDs) n In an FD, X Y, knowing the value of X means that you know the unique value for Y. n In an MVD, X Y, knowing the value of X means that you know the set of values from which Y can come. www. assignmentpoint. com

Example of MVD n Assume we have two streams for some course, taught by different instructors, and that for each course, we use two textbooks. n Example: course CS 51 T CS 52 S instructor Rao Mansingh Rao Stitt text Date Korth Jackson Rich www. assignmentpoint. com

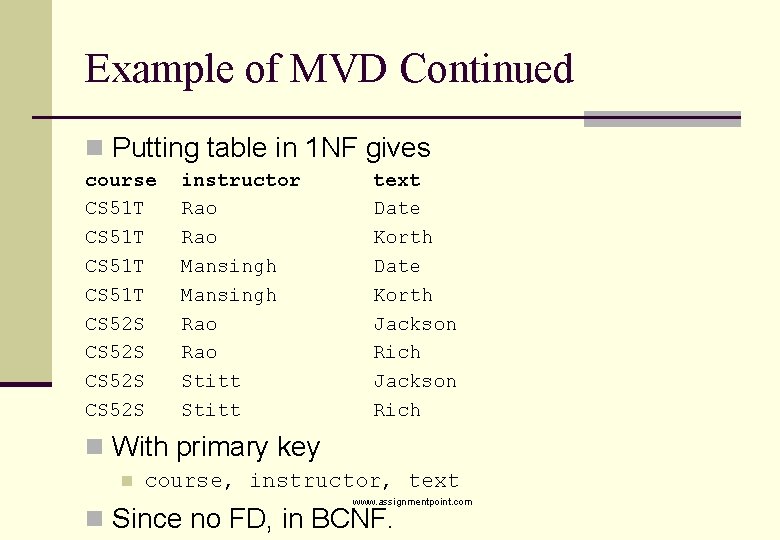
Example of MVD Continued n Putting table in 1 NF gives course CS 51 T CS 52 S instructor Rao Mansingh Rao Stitt text Date Korth Jackson Rich n With primary key n course, instructor, text www. assignmentpoint. com n Since no FD, in BCNF.

Redundancy because of MVDs n However, still redundancy in the table because n if <c, p, x> and <c, p’, x’> in table <c, p’, x> and <c, p, x’> in table too. n The table contains two multivalued dependencies: n course instructor n course text n Danger of insertion and update anomalies www. assignmentpoint. com

Fourth Normal Form n Under 4 NF, a relation should not contain two or more independent MVDs. n In other words, if there is a MVD, X Y, then X should be a superkey. www. assignmentpoint. com

Getting Tables into 4 NF n Again, get a table into 4 NF through decomposition so that each MVD is captured in a separate table. n Example: CP(course, instructor) n CT(course, text) n www. assignmentpoint. com

Normalization Reconsidered n Normalization helps avoid: n Insertion anomalies n Update anomalies n Deletion anomalies n Normalization increases retrieval time for some queries. www. assignmentpoint. com