Data warehouse Ch 4 Clustering Prepared by Dr

Data warehouse Ch. 4 Clustering Prepared by Dr. Maher Abuhamdeh

Clustering Definition v Given a set of data points, each having a set of attributes, and a similarity measure among them, find clusters such that § Data points in one cluster are more similar to one another. § Data points in separate clusters are less similar to one another. v Cluster analysis § Grouping a set of data objects into clusters v Clustering is unsupervised Learning: no predefined classes 2

Clustering: Application 1 v Market Segmentation: § Goal: subdivide a market into distinct subsets of customers where any subset may conceivably be selected as a market target to be reached with a distinct marketing mix. § Approach: • Collect different attributes of customers based on their geographical and lifestyle related information. • Find clusters of similar customers. • Measure the clustering quality by observing buying patterns of customers in same cluster vs. those from different clusters. 3

Clustering: Application 2 v Document Clustering: § Goal: To find groups of documents that are similar to each other based on the important terms appearing in them. § Approach: To identify frequently occurring terms in each document. Form a similarity measure based on the frequencies of different terms. Use it to cluster. § Gain: Information Retrieval can utilize the clusters to relate a new document or search term to clustered documents. 4

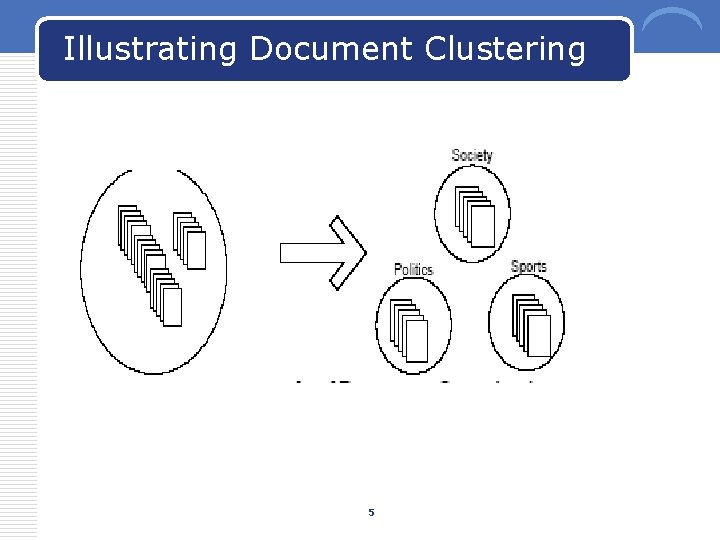
Illustrating Document Clustering 5

Illustrating Document Clustering v Clustering Points: 3204 Articles of Los Angeles Times. v Similarity Measure: How many words are common in these documents (after some word filtering). 6

What are some typical application of clustering? v Spatial Data Analysis § Create thematic maps in GIS by clustering feature spaces § Detect spatial clusters or for other spatial mining tasks v Image Processing v Economic Science (especially market research) v WWW § Document classification § Cluster Weblog data to discover groups of similar access patterns January 22, 2022 Data Mining: Concepts 7

Examples of Clustering Applications v Marketing: Help marketers discover distinct groups in their customer bases, and then use this knowledge to develop targeted marketing programs v Land use: Identification of areas of similar land use in an earth observation database v Insurance: Identifying groups of motor insurance policy holders with a high average claim cost v City-planning: Identifying groups of houses according to their house type, value, and geographical location v Earth-quake studies: Observed earth quake epicenters should be clustered along continent faults January 22, 2022 Data Mining: Concepts 8

Quality: What Is Good Clustering? v A good clustering method will produce high quality clusters with § high intra-class similarity (Points close to each other) § low inter-class similarity (cluster is different from each other) v The quality of a clustering result depends on both the similarity measure used by the method and its implementation v The quality of a clustering method is also measured by its ability to discover some or all of the hidden patterns January 22, 2022 Data Mining: Concepts 9

Requirements of Clustering in Data Mining v Scalability (Many cluster algorithms work well on small data) v Ability to deal with different types of attributes (numerical data) v Ability to handle dynamic data v Discovery of clusters with any kind of shape (Euclidean or Manhattan distance measures) v Minimal requirements for domain knowledge to determine input parameters ( Number of clusters K) v Able to deal with noise and outliers (some clustering algorithm are sensitive to such data and may lead to poor quality) v High dimensionality (Several dimensions or attributes) v Constraints based clustering January 22, 2022 Data Mining: Concepts 10

Approaches v K-Means v K-Medoids v Self-Organizing Maps (SOM) 11

Simple Clustering: K-means Works with numeric data only 1) Pick a number (K) of cluster centers (at random) 2) Assign every item to its nearest cluster center (e. g. using Euclidean distance) 3) Move each cluster center to the mean of its assigned items 4) Repeat steps 2, 3 until convergence (change in cluster assignments less than a threshold) 12

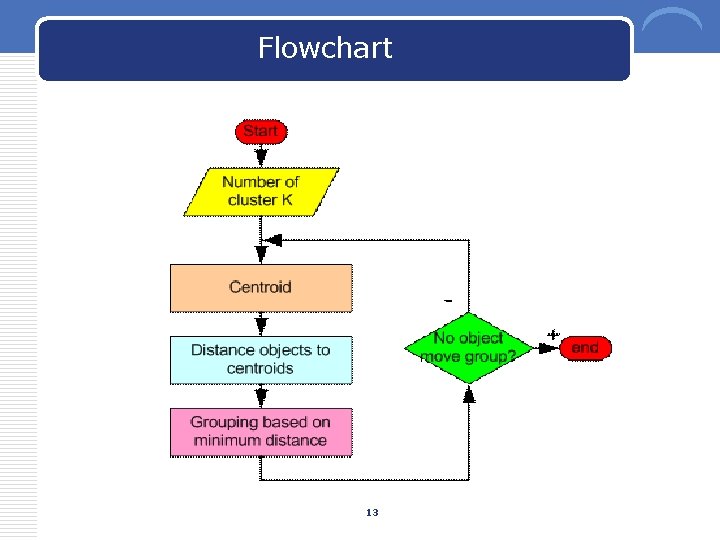
Flowchart 13

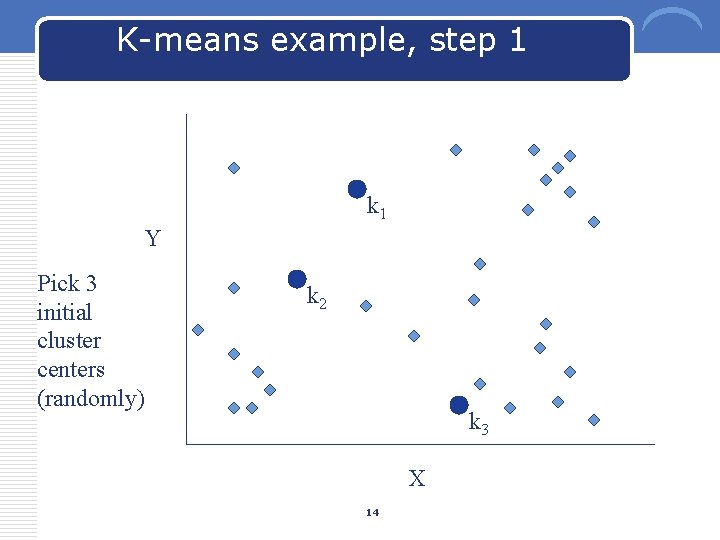
K-means example, step 1 k 1 Y Pick 3 initial cluster centers (randomly) k 2 k 3 X 14

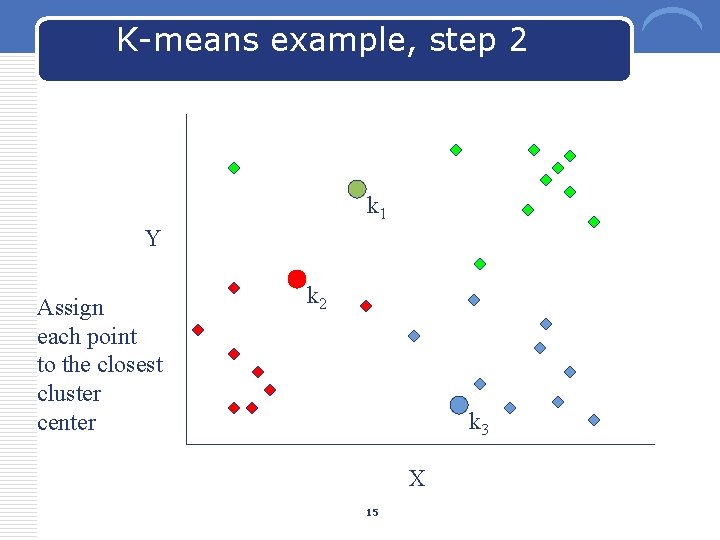
K-means example, step 2 k 1 Y Assign each point to the closest cluster center k 2 k 3 X 15

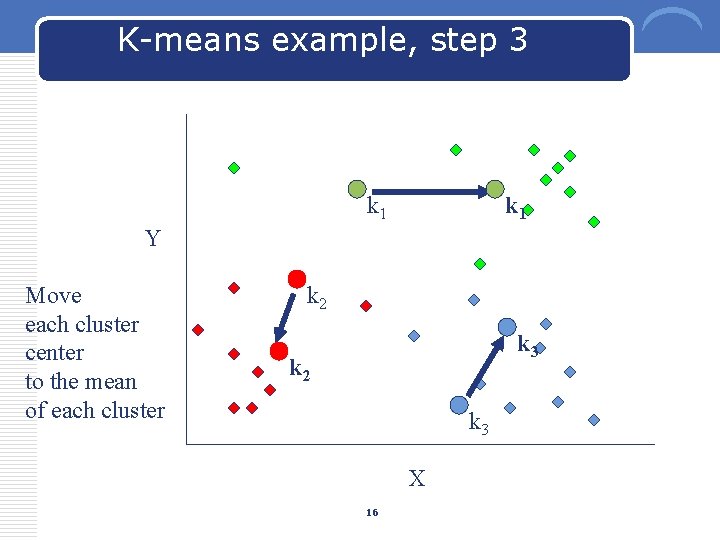
K-means example, step 3 k 1 Y Move each cluster center to the mean of each cluster k 2 k 3 X 16

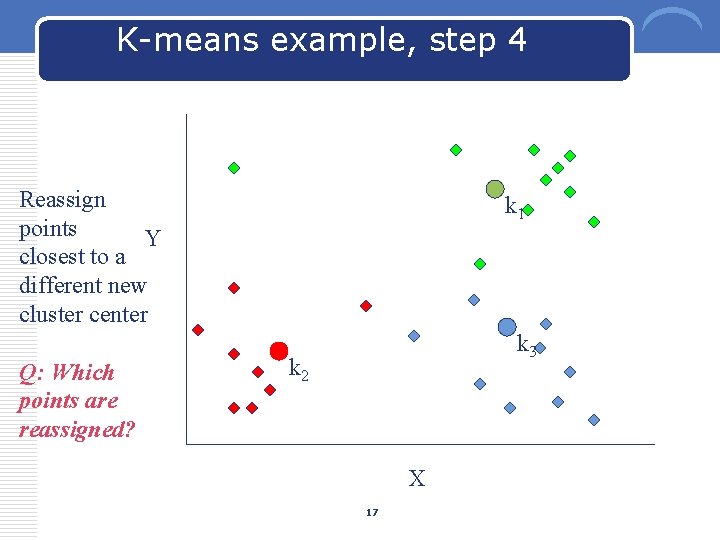
K-means example, step 4 Reassign points Y closest to a different new cluster center Q: Which points are reassigned? k 1 k 3 k 2 X 17

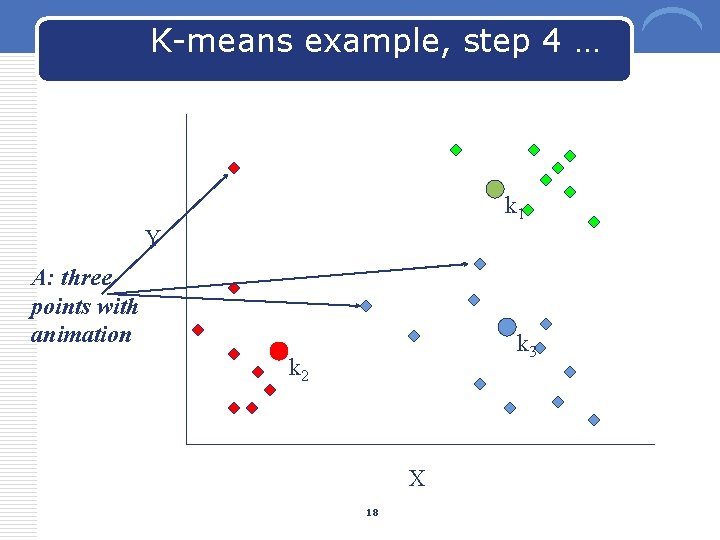
K-means example, step 4 … k 1 Y A: three points with animation k 3 k 2 X 18

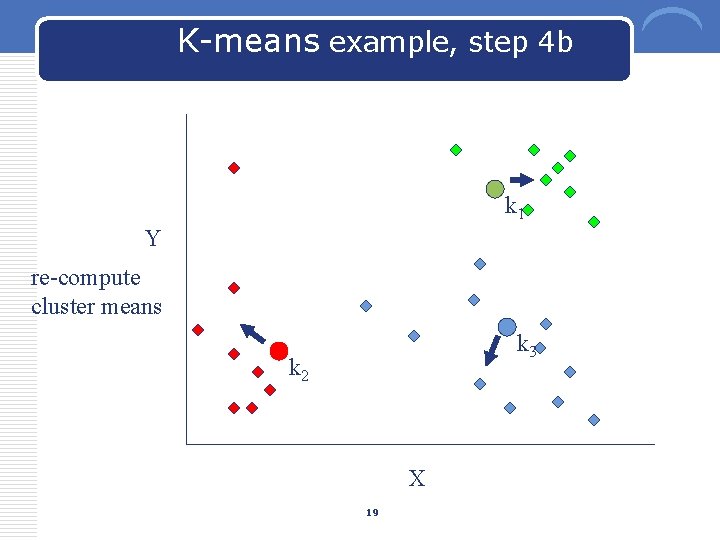
K-means example, step 4 b k 1 Y re-compute cluster means k 3 k 2 X 19

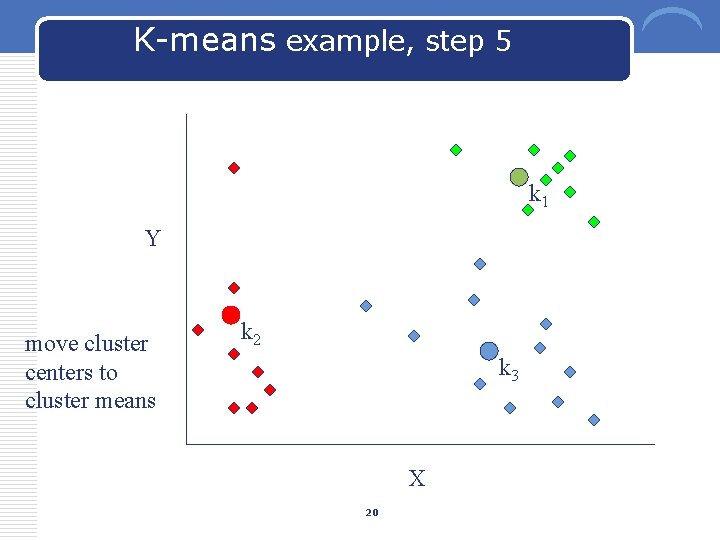
K-means example, step 5 k 1 Y move cluster centers to cluster means k 2 k 3 X 20

example v Suppose we have several objects (4 types of medicines) and each object have two attributes or features as shown in table below. Our goal is to group these objects into K=2 group of medicine based on the two features (p. H and weight index). Object attribute 1 (X): weight index attribute 2 (Y): p. H Medicine A 1 1 Medicine B 2 1 Medicine C 4 3 Medicine D 5 4 21

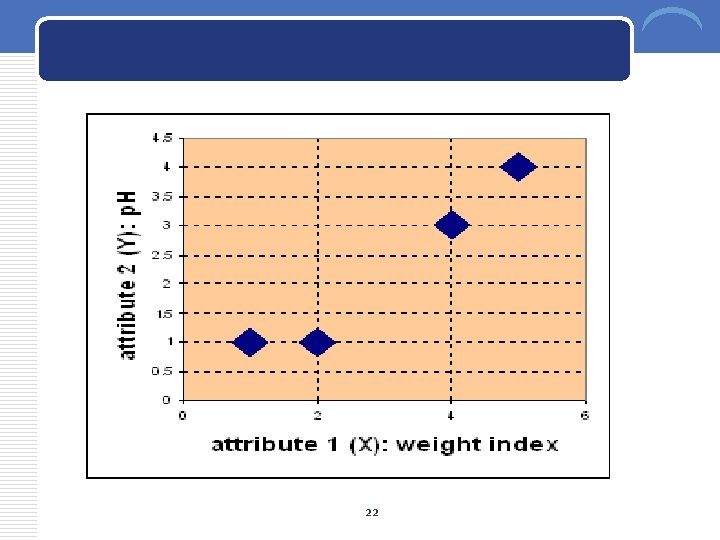
22

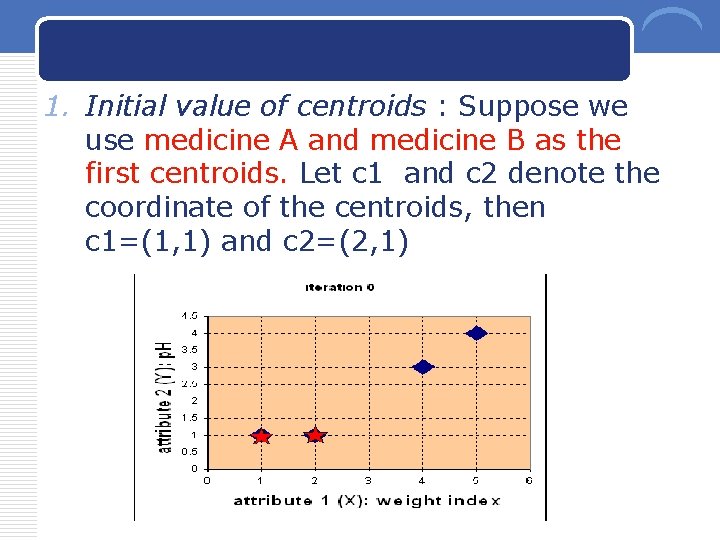
1. Initial value of centroids : Suppose we use medicine A and medicine B as the first centroids. Let c 1 and c 2 denote the coordinate of the centroids, then c 1=(1, 1) and c 2=(2, 1) 23

2. Objects-Centroids distance : we calculate the distance between cluster centroid to each object. Let us use Euclidean distance, then we have distance matrix at iteration 0 is 24

3. Objects clustering : We assign each object based on the minimum distance. Thus, medicine A is assigned to group 1, medicine B to group 2, medicine C to group 2 and medicine D to group 2. The element of Group matrix below is 1 if and only if the object is assigned to that group. 25

4. Iteration-1, determine centroids : Knowing the members of each group, now we compute the new centroid of each group based on these new memberships. Group 1 only has one member thus the centroid remains in Group 2 now has three members, thus the centroid is the average coordinate among the three members 26

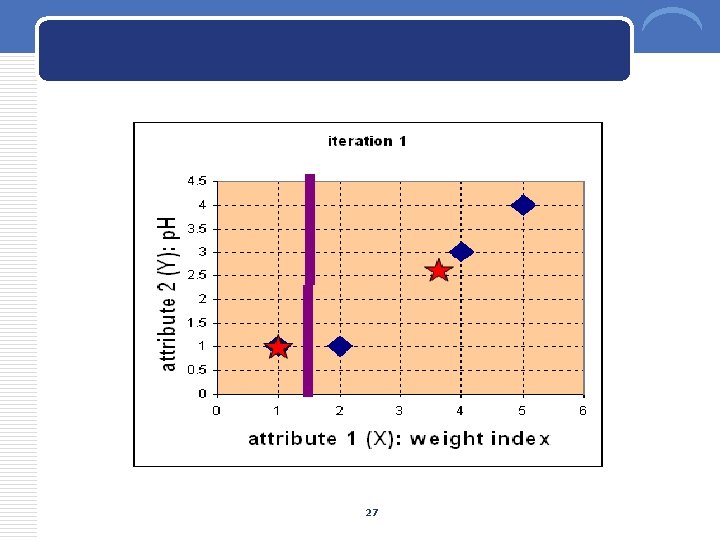
27

5. Iteration-1, Objects-Centroids distances : The next step is to compute the distance of all objects to the new centroids. Similar to step 2, we have distance matrix at iteration 1 is 28

6. Iteration-1, Objects clustering: Similar to step 3, we assign each object based on the minimum distance. Based on the new distance matrix, we move the medicine B to Group 1 while all the other objects remain. The Group matrix is shown below 29

7. Iteration 2, determine centroids: Now we repeat step 4 to calculate the new centroids coordinate based on the clustering of previous iteration. Group 1 and group 2 both has two members, thus the new centroids are and 30

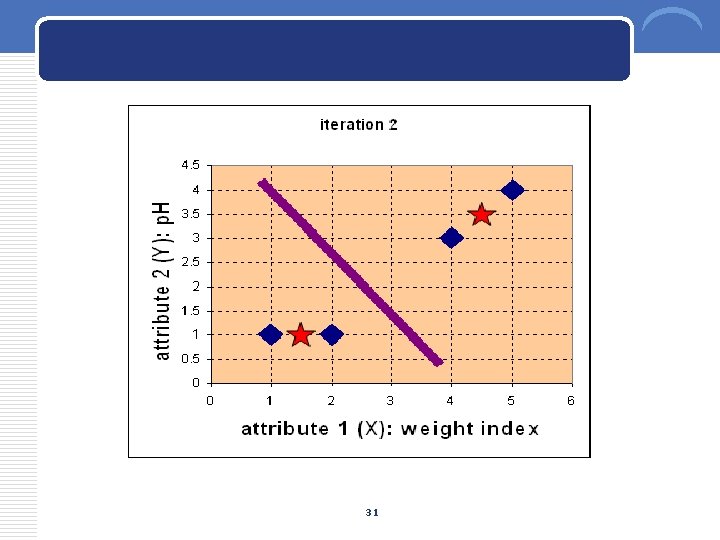
31

8. Iteration-2, Objects-Centroids distances : Repeat step 2 again, we have new distance matrix at iteration 2 as 32

9. Iteration-2, Objects clustering: Again, we assign each object based on the minimum distance We obtain result that G 1=G 2, Comparing the grouping of last iteration and this iteration reveals that the objects does not move group anymore. Thus, the computation of the k-mean clustering has reached its stability and no more iteration is needed 33

v We get the final grouping as the results Object Feature 1 (X): weight index Feature 2 (Y): p. H Group (result) Medicine A 1 1 1 Medicine B 2 1 1 Medicine C 4 3 2 Medicine D 5 4 2 34

pseudo code for k means clustering algorithm v Initialize clustering v Loop until done v Compute mean of each cluster update v Clustering based on new means v End loop 35

K-Means Properties Advantages c K-means is relatively scalable and efficient in processing large data sets Disadvantage c Can be applied only when the mean of a cluster is defined c Users need to specify k c K-means is not suitable for discovering clusters with nonconvex shapes or clusters of very different size c It is sensitive to noise and outlier data points (can influence the mean value)