Data types declarations and expressions in Java Variables

Data types, declarations, and expressions in Java

Variables • A variable is a named memory location capable of storing data • As we have already seen, object variables refer to objects, which are created by instantiating classes with the new operator • We can also store data in simple variables, which represent data only, without any associated methods

Data declaration syntax • The syntax for the declaration of a variable is: Data type identifier; – “data type” may be the name of a class, as we have seen, or may be one of the simple types, which we’ll see in a moment – “identifier” is a legal Java identifier; the rules for simple variable identifiers are the same as those for object identifiers

Variable declaration: examples • For example: int age; // int means integer double cash. Amount; // double is a real # • We can also declare multiple variables of the same type using a single instruction; for example: int x, y, z; // or int x, y, z; • The second way is preferable, because it’s easier to document the purpose of each variable this way.

Numeric data types in Java: integers Data type name Minimum value Maximum value byte -128 127 short -32, 768 32, 767 int -2, 147, 483, 648 2, 147, 483, 647 long -9, 223, 372, 036, 854, 775, 808 9, 223, 372, 036, 854, 775, 807

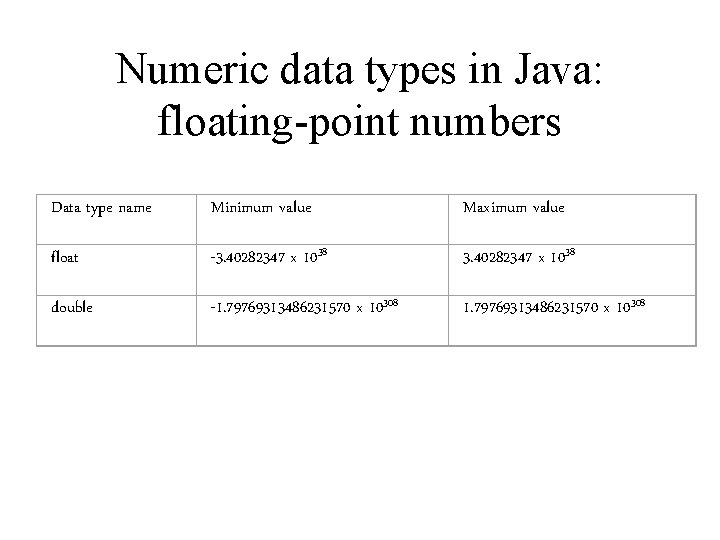
Numeric data types in Java: floating-point numbers Data type name Minimum value Maximum value float -3. 40282347 x 1038 double -1. 79769313486231570 x 10308

Numeric data types: some notes • Most programmers use int for whole numbers and double for real numbers • Numeric data types in Java are primitive (nonobject) types; this means that a numeric variable is somewhat different from an object: – You don’t use the new operator to initialize a numeric variable – just assign it a value – Memory for a numeric variable is allocated at declaration – Numeric variables actually store values; object names store addresses

Scientific notation and real numbers • Both float and double have wide ranges to the values they can represent • In order to save space, particularly large or small values are often displayed by default using a variation of scientific notation • For example, the value. 0000258 would appear as 2. 58 x 10 -5 in conventional notation – as output from a Java program, the number would appear as 2. 58 e-5 • The ‘e’ is for exponent, and can be upper or lowercase

Assignment statements • We can store a value in a variable using an assignment statement • Assignment statement syntax: variable. Name = expression; – variable. Name must be the name of a declared variable – expression must evaluate to an appropriate value for storage within the type of variable specified

Arithmetic expressions • An expression is a set of symbols that represents a value • An arithmetic expression represents a numeric value • Simple expressions are single values; examples: 18 -4 1. 245 e 3 • Previously-declared and initialized variables or constants can also be simple expressions

Arithmetic operators in Java • Compound expressions are formed by combining simple expressions using arithmetic operators Operation Symbol Addition + Subtraction - Multiplication * Division / Modulus %

Arithmetic operations in Java • As in algebra, multiplication and division (and modulus, which we’ll look at momentarily) take precedence over addition and subtraction • We can form larger expressions by adding more operators and more operands – Parentheses are used to group expressions, using the same rule as in algebra: evaluate the innermost parenthesized expression first, and work your way out through the levels of nesting – The one complication with this is we have only parentheses to group with; you can’t use curly or square brackets, as they have other specific meanings in Java

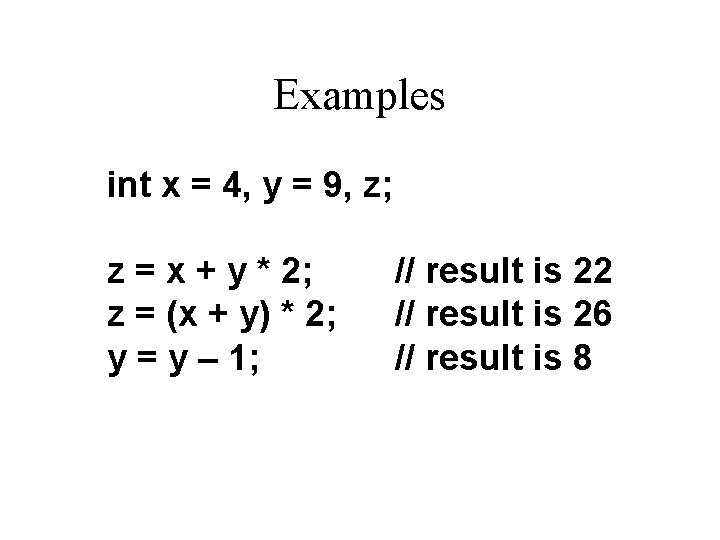
Examples int x = 4, y = 9, z; z = x + y * 2; z = (x + y) * 2; y = y – 1; // result is 22 // result is 26 // result is 8

Integer division • When one real number is divided by another, the result is a real number; for example: double x = 5. 2, y = 2. 0, z; z = x / y; // result is 2. 6 • When dividing integers, we get an integer result • For example: int x = 4, y = 9, z; z = x / 2; // result is 2 z = y / x; // result is 2, again z = x / y; // result is 0

Integer division • There are two ways to divide integers – using the / operator, produces the quotient of the two operands – using the % operator, produces the remainder when the operands are divided. This is called modular division, or modulus (often abbreviated mod). For example: int z = z = x x y x = % % % 4, y = 2; // x; // y; // 9, z; result is 0 result is 1 result is 4

Mixed-type expressions • A mixed-type expression is one that involves operands of different data types – Like other expressions, such an expression will evaluate to a single result – The data type of that value will be the type of the operand with the highest precision – What this means, for all practical purposes, is that, if an expression that involves both real numbers and whole numbers, the result will be a real number. • The numeric promotion that takes place in a mixed-type expression is also known as implicit type casting

Explicit type casting • We can perform a deliberate type conversion of an operand or expression through the explicit cast mechanism • Explicit casts mean the operand or expression is evaluated as a value of the specified type rather than the type of the actual result • The syntax for an explicit cast is: (data type) operand -or(data type) (expression)

Explicit type casts - examples int x = 2, y = 5; double z; z = (double) y / z; z = (double) (y / z); // z = 2. 5 // z = 2. 0

Assignment conversion • Another kind of implicit conversion can take place when an expression of one type is assigned to a variable of another type • For example, an integer can be assigned to a real-number type variable; in this case, an implicit promotion of the integer value occurs

No demotions in assignment conversions • In Java we are not allowed to “demote” a higherprecision type value by assigning it to a lowerprecision type variable • Instead, we must do an explicit type cast. Some examples: int x = 10; double y = x; x = y; y = y / 3; x = (int)y; // this is allowed; y = 10. 0 // error: can’t demote value to int // y now contains 3. 33333333 // allowed; x = 3

Compound arithmetic/assignment operators • Previous examples in the notes have included the following statements: y = y + 1; y = y / 3; • In each case, the current value of the variable is used to evaluate the expression, and the resulting value is assigned to the variable (erasing the previously-stored value) • This type of operation is extremely common; so much so, that Java (like C++ and C before it) provides a set of shorthand operators to perform this type of operation. The table on the next slide illustrates the use and meaning of these operators

Compound arithmetic/assignment operators Operator Use Meaning += X += 1; X = X + 1; -= X -= 1; X = X – 1; *= X *= 5; X = X * 5; /= X /= 2; X = X / 2; %= X %= 10; X = X % 10;

Named constants • A variable is a named memory location that can hold a value of a specific data type; as we have seen, the value stored at this location can change throughout the execution of a program • If we want to maintain a value in a named location, we use the Java keyword final in the declaration and immediately assign the desired value; with this mechanism, we declare a named constant. Some examples: final int LUCKY = 7; final double PI = 3. 14159; final double LIGHTSPEED = 3. 0 e 10. 0 ;

Named constants • The name of the constant is used in expressions but cannot be assigned a new value. For example, to calculate the value of variable circle. Area using the variable radius and the value , we could write: circle. Area = 2 * PI * radius; • The use of named constants is considered good programming practice, because it: – eliminates (or at least minimizes) the use of “magic” numbers in a program; it is easier to read code that contains meaningful names – allows a programmer to make global changes in calculations easily

Using named constants: example • Suppose, for example, that you are writing a program that involves adding sales tax and subtracting discounts from users’ totals • If the tax rate is 5% and the discount rate is 10%, the calculation could look like this: total = total – (total *. 1) + ((total *. 1) * (1 +. 05)); • By itself, this isn’t too bad; but suppose there are several places in the program that use these values?

Example continued • If, for example, the discount changes to 12%, the programmer who has to maintain the code would have to change the value. 1 to. 12 everywhere in the program – at least, everywhere that it actually refers to the discount. – The value. 1 could very well mean something else in a different expression. – If we use named constants instead, the value has to change in just one place, and there is no ambiguity about what the number means in context; with named constants, the revised code might read: total = total – (total * discount) + ((total * discount) * (1 + taxrate));

Calculations using Java’s Math class • The standard Java class Math contains class methods and constants that are useful in performing calculations that go beyond simple arithmetic operations • The constants defined in the Math class are Math. PI and Math. E, which are defined values for and e (the base for natural logs), respectively

Math class methods • Math. abs(a): returns the absolute value of its argument (a), which can be of type int, long, float, or double • Math. sin(a): returns the sine of its argument, a double value representing an angle in radians; similar trigonometric functions include Math. cos(a) for cosine, Math. tan(a) for tangent, Math. acos(a), Math. asin(a) and Math. atan(a), which provide arccosine, arcsine, and arctangent, respectively

Math class methods • Math. to. Degrees(a): converts a, a double value representing an angle in radians, to the corresponding value in degrees • Math. to. Radians(a): converts a, a double value representing an angle in degrees to the corresponding value in radians

Math class methods • Math. sqrt(a): returns the square root of a, a value of type double • Math. cbrt(a): returns the cube root of a, a value of type double • Math. pow(a, b): returns the value of ab • Math. log(a): returns the natural log of a, a double value • Math. log 10(a): returns the log base 10 of a, a double value

Example // computing the roots of a quadratic equation: double a, // coefficient of x squared b, // coefficient of x c, // 3 rd term in equation x 1, // first root x 2; // second root // read in values for a, b, and c – not shown here … x 1 = (-b + Math. sqrt(Math. pow(b, 2) – (4 * a * c))) / (2 * a); x 2 = (-b - Math. sqrt(Math. pow(b, 2) – (4 * a * c))) / (2 * a);