Data Structures Using C 2 E Chapter 8

Data Structures Using C++ 2 E Chapter 8 Queues Edited by Malak Abdullah Jordan University of Science and Technology

Introduction • Queue data structure – Elements added at one end (rear), deleted from other end (front) – First In First Out (FIFO) – Middle elements inaccessible 2

Queue Operations • Two key operations – add. Queue – delete. Queue • Additional operations – initialize. Queue, is. Empty. Queue, is. Full. Queue, front, back • queue. Front, queue. Rear pointers – Keep track of front and rear • See code on pages 453 -454 3

Implementation of Queues as Arrays • Four member variables – Array to store queue elements – Variables queue. Front, queue. Rear – Variable max. Queue. Size • Using queue. Front, queue. Rear to access queue elements – queue. Front: first queue element index – queue. Rear: last queue element index • queue. Front changes after each delete. Queue operation • queue. Rear changes after each add. Queue operation 4

Empty Queue 0 list max. Size 20 front 0 rear 19 count 0 1 2 3 4 5 6 . . . . 19

add. Queue(‘R’) 0 list max. Size 20 front 0 rear 0 count 1 R 1 2 3 4 5 6 . . . . 19

add. Queue(‘T’) list max. Size 20 front 0 rear 1 count 2 0 1 R T 2 3 4 5 6 . . . . 19

add. Queue(‘P’) list max. Size 20 front 0 rear 2 count 3 0 1 2 R T P 3 4 5 6 . . . . 19

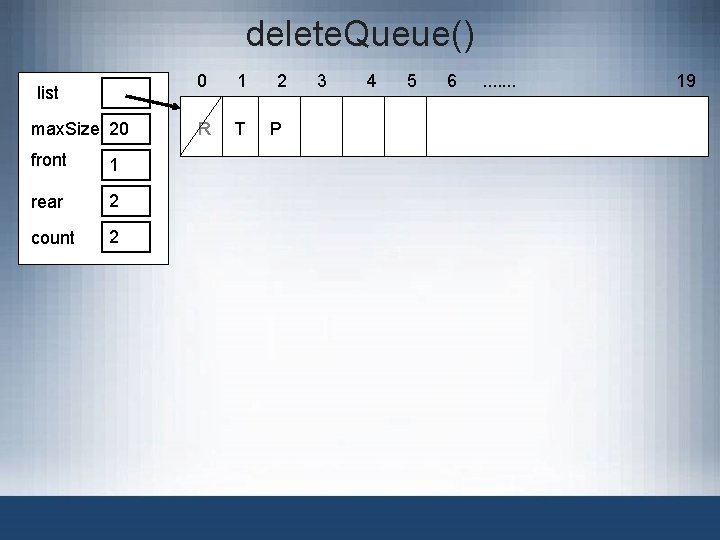
delete. Queue() list max. Size 20 front 1 rear 2 count 2 0 1 2 R T P 3 4 5 6 . . . . 19

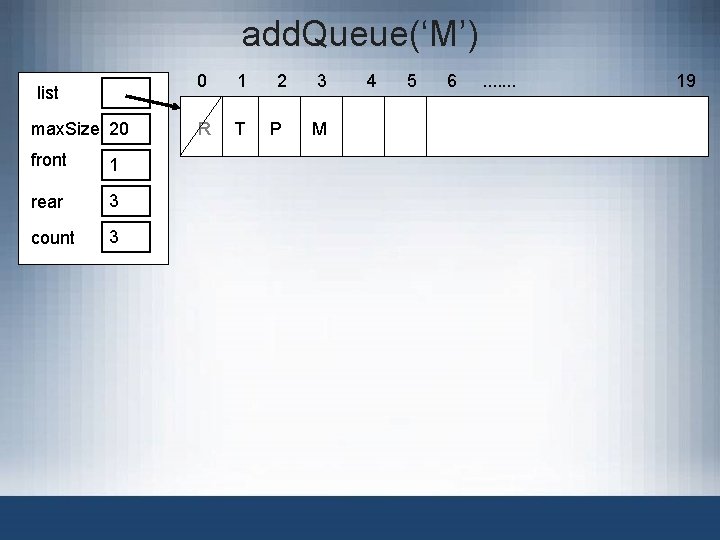
add. Queue(‘M’) list max. Size 20 front 1 rear 3 count 3 0 1 2 3 R T P M 4 5 6 . . . . 19

Implementation of Queues as Arrays (cont’d. ) • Execute operation – add. Queue(Queue, 'A'); • Execute – add. Queue(Queue, 'B'); – add. Queue(Queue, 'C'); • Execute – delete. Queue(); Data Structures Using C++ 2 E 11

FIGURE 8 -1 Queue after the first add. Queue operation FIGURE 8 -2 Queue after two more add. Queue operations FIGURE 8 -3 Queue after the delete. Queue operation Data Structures Using C++ 2 E 12

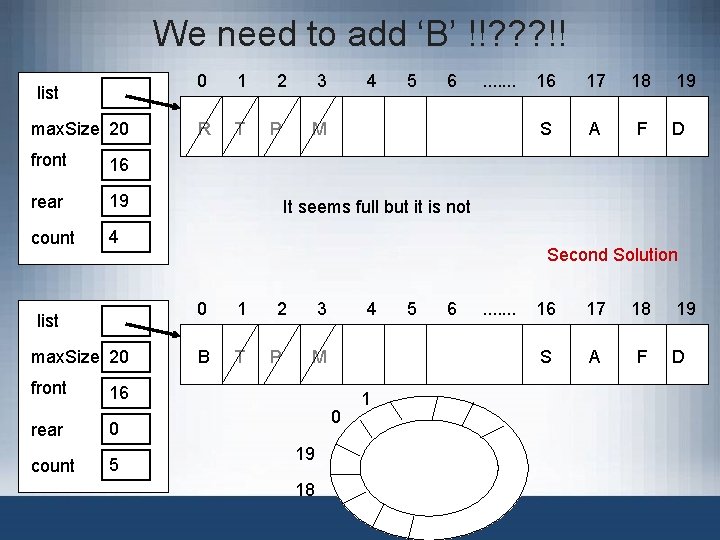
Implementation of Queues as Arrays (cont’d. ) • Consider the sequence of operations: AAADADADADA. . . – Eventually index queue. Rear points to last array position • Looks like a full queue • Reality: queue has two or three elements, array empty in the front FIGURE 8 -4 Queue after the sequence of operations AAADADADA. . . Data Structures Using C++ 2 E 13

Implementation of Queues as Arrays (cont’d. ) • First solution – Upon queue overflow to the rear • Check value of queue. Front • If room in front: slide all queue elements toward first array position – Works if queue size very small • Second solution: assume circular array FIGURE 8 -5 Circular queue Data Structures Using C++ 2 E 14

We need to add ‘B’ !!? ? ? !! list max. Size 20 front 16 rear 19 count 4 list max. Size 20 front 0 rear 4 count 5 0 1 2 3 R T P M 4 5 6 . . . . 16 17 18 S A F 19 D It seems full but it is not First Solution 0 1 S A 2 F 3 D 4 5 6 . . . . 16 17 18 19 B Imagine 1000000 elements? ?

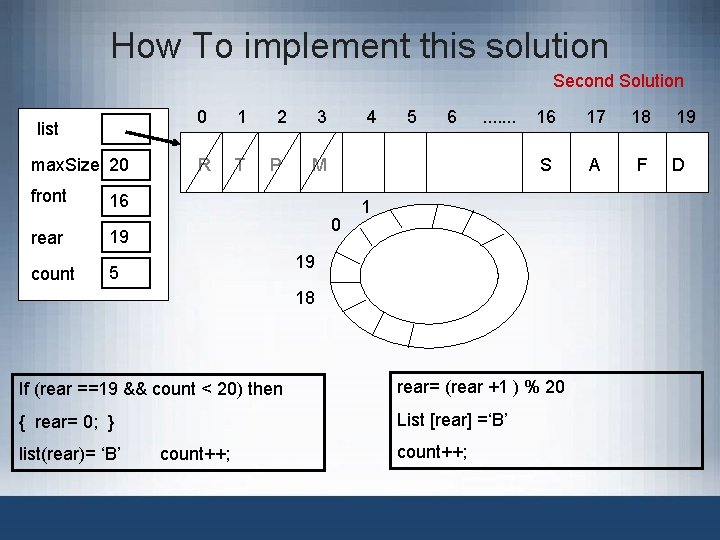
We need to add ‘B’ !!? ? ? !! list max. Size 20 front 16 rear 19 count 4 list max. Size 20 front 16 rear 0 count 5 0 1 2 3 R T P M 4 5 6 . . . . 16 17 18 S A F 19 D It seems full but it is not Second Solution 0 1 2 3 B T P M 4 0 19 18 1 5 6 . . . . 16 17 18 S A F 19 D

How To implement this solution Second Solution list max. Size 20 front 16 rear 19 count 5 0 1 2 3 R T P M 4 0 5 6 . . . . 16 17 18 S A F 1 19 18 If (rear ==19 && count < 20) then rear= (rear +1 ) % 20 { rear= 0; } List [rear] =‘B’ list(rear)= ‘B’ count++; 19 D

Implementation of Queues as Arrays(cont’d. ) • queue. Rear = (queue. Rear + 1) % max. Queue. Size; – Advances queue. Rear (queue. Front) to next array position FIGURE 8 -6 Queue before and after the add operation Data Structures Using C++ 2 E 18

Implementation of Queues as Arrays(cont’d. ) f r • If queue. Rear < max. Queue. Size – 1 – queue. Rear + 1 <= max. Queue. Size – 1 – (queue. Rear + 1) % max. Queue. Size = queue. Rear + 1 0 f r • If queue. Rear == max. Queue. Size – 1 – queue. Rear + 1 == max. Queue. Size – (queue. Rear + 1) % max. Queue. Size = 0 queue. Rear set to zero – First array position Data Structures Using C++ 2 E 19

Implementation of Queues as Arrays (cont’d. ) • Two cases with identical queue. Front, queue. Rear values – Figure 8 -7(b) represents an empty queue – Figure 8 -8(b) represents a full queue FIGURE 8 -7 Queue before and after the delete operation FIGURE 8 -8 Queue before and after the add operation Data Structures Using C++ 2 E 20

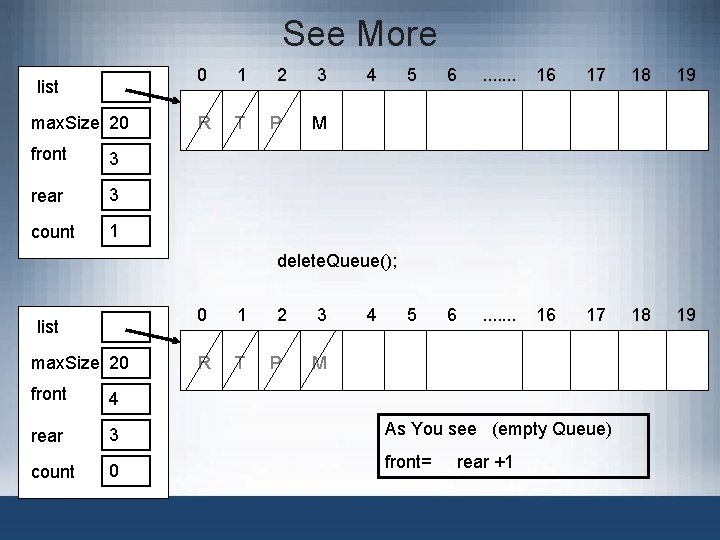
See More list max. Size 20 front 3 rear 3 count 1 0 1 2 3 R T P M 4 5 6 . . . 16 17 18 19 delete. Queue(); list max. Size 20 front 4 rear 3 count 0 0 1 2 3 R T P M 4 As You see (empty Queue) front= rear +1

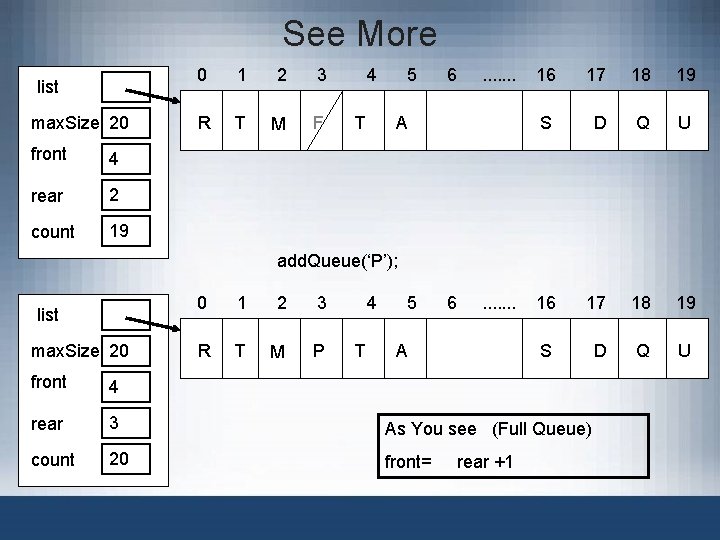
See More list max. Size 20 front 4 rear 2 count 19 0 1 2 3 R T M F 4 T 5 6 . . . . A 16 17 18 19 S D Q U add. Queue(‘P’); list max. Size 20 0 1 2 3 R T M P 4 T 5 6 . . . . A front 4 rear 3 As You see (Full Queue) count 20 front= rear +1

Implementation of Queues as Arrays (cont’d. ) • First solution: use variable count – Incremented when new element added – Decremented when element removed – Functions initialize. Queue, destroy. Queue initialize count to zero Data Structures Using C++ 2 E 23

Implementation of Queues as Arrays (cont’d. ) • Second solution – queue. Front indicates index of array position preceding first element of the queue – Assume queue. Rear indicates index of last element • Empty queue if queue. Front == queue. Rear – Slot indicated by index queue. Front is reserved – Queue is full • If next available space represents special reserved slot Data Structures Using C++ 2 E 24

Implementation of Queues as Arrays (cont’d. ) FIGURE 8 -9 Array to store the queue elements with a reserved slot • See code on pages 459 -460 – Uses first solution Data Structures Using C++ 2 E 25

Empty Queue and Full Queue • Empty queue – If count == 0 • Full queue – If count == max. Queue. Size Data Structures Using C++ 2 E 26

Initialize Queue • Initializes queue to empty state – First element added at the first array position – Initialize queue. Front to zero, queue. Rear to max. Queue. Size - one, count to zero FIGURE 8 -10 Empty queue Data Structures Using C++ 2 E 27

Front • Returns first queue element – If the queue nonempty • Element indicated by index queue. Front returned – Otherwise • Program terminates Data Structures Using C++ 2 E 28

Back • Returns last queue element – If queue nonempty • Returns element indicated by index queue. Rear – Otherwise • Program terminates Data Structures Using C++ 2 E 29

Add Queue Data Structures Using C++ 2 E 30

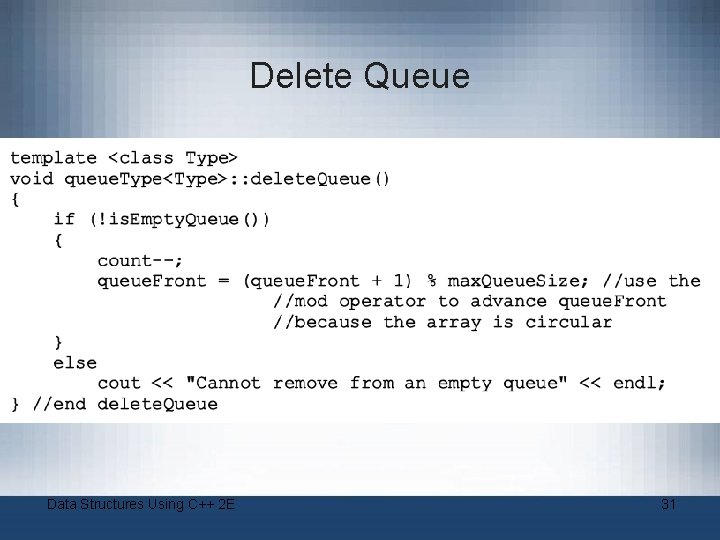
Delete Queue Data Structures Using C++ 2 E 31

Constructors and Destructors Data Structures Using C++ 2 E 32

Constructors and Destructors (cont’d. ) • Array storing queue elements – Created dynamically – When queue object goes out of scope • Destructor deallocates memory occupied by the array storing queue elements Data Structures Using C++ 2 E 33

Linked Implementation of Queues • Array implementation issues – Fixed array size • Finite number of queue elements – Requires special array treatment with the values of the indices queue. Front, queue. Rear • Linked implementation of a queue – Simplifies special cases of the array implementation – Queue never full • See code on pages 464 -465 Data Structures Using C++ 2 E 34

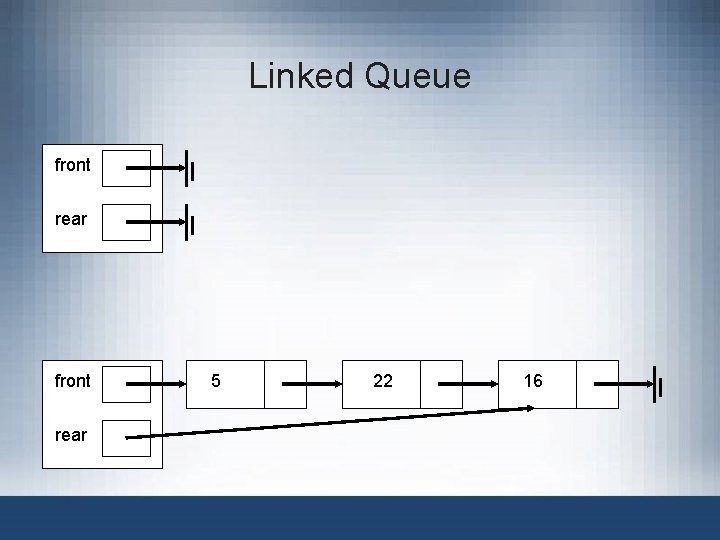
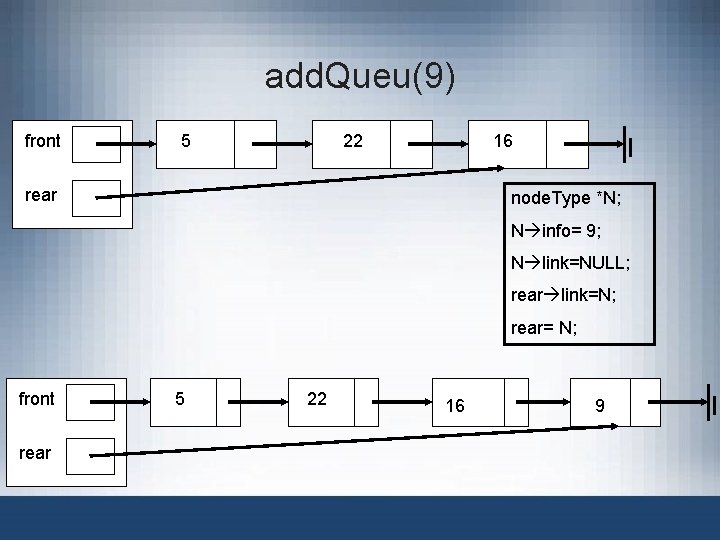
Linked Queue front rear 5 22 16

add. Queu(9) front 5 22 16 rear node. Type *N; N info= 9; N link=NULL; rear link=N; rear= N; front rear 5 22 16 9

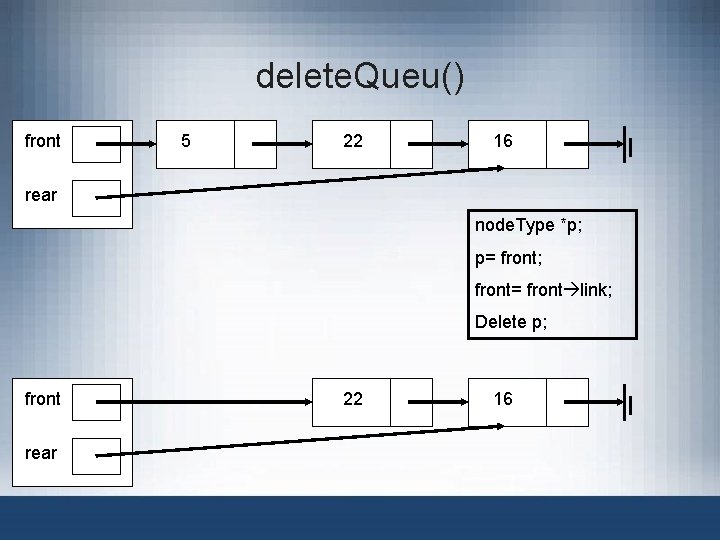
delete. Queu() front 5 22 16 rear node. Type *p; p= front; front= front link; Delete p; front rear 22 16

Empty and Full Queue • Empty queue if queue. Front is NULL • Memory allocated dynamically – Queue never full – Function implementing is. Full. Queue operation returns the value false Data Structures Using C++ 2 E 38

Initialize Queue • Initializes queue to an empty state – Empty if no elements in the queue Data Structures Using C++ 2 E 39

add. Queue, front, back, and delete. Queue Operations • add. Queue operation adds a new element at end of the queue – Access the pointer queue. Rear Data Structures Using C++ 2 E 40

add. Queue, front, back, and delete. Queue Operations (cont’d. ) • If queue nonempty – Operation front returns first element – Element indicated queue. Front returned • If queue empty: front terminates the program Data Structures Using C++ 2 E 41

add. Queue, front, back, and delete. Queue Operations (cont’d. ) • If queue nonempty – Operation back returns last element – Element indicated by queue. Rear returned • If queue empty: back terminates the program Data Structures Using C++ 2 E 42

add. Queue, front, back, and delete. Queue Operations (cont’d. ) • If queue nonempty – Operation delete. Queue removes first element • Access pointer queue. Front Data Structures Using C++ 2 E Edited by Malak Abdullah Jordan University of Science and Technology 43

add. Queue, front, back, and delete. Queue Operations (cont’d. ) • Default constructor – When queue object goes out of scope • Destructor destroys the queue • Deallocates memory occupied by the queue elements – Function definition similar to function initialize. Queue Data Structures Using C++ 2 E 44

Queue Derived from the class unordered. Linked. List. Type • Linked queue implementation – Similar to forward manner linked list implementation – Similar operations • add Queue, insert. First • initialize. Queue , initialize. List • is. Empty. Queue, is. Empty. List – delete. Queue operation implemented as before – Same pointers • queue. Front and first, queue. Rear and last Data Structures Using C++ 2 E 45

Queue Derived from the class unordered. Linked. List. Type (cont’d. ) • Linked queue implementation (cont’d. ) – Can derive the class to implement the queue from the class linked. List. Type – class linked. List. Type • An abstract • Does not implement all operations – class unordered. Linked. List. Type • Derived from class linked. List. Type • Provides definitions of the abstract functions of the class linked. List. Type Data Structures Using C++ 2 E 46

STL class queue (Queue Container Adapter) • Standard Template Library (STL) – Provides a class to implement queues in a program – Queue • Name of class defining the queue • Name of header defining class queue Data Structures Using C++ 2 E 47

STL class queue (cont’d. ) • Queue container class – Provides relational operators comparing two queues • See Example 8 -2 TABLE 8 -1 Operations on a queue object Data Structures Using C++ 2 E 48

Priority Queues • Queue structure ensures items processed in the order received • Priority queues – Customers (jobs) with higher priority pushed to the front of the queue • Implementation – Ordinary linked list • Keeps items in order from the highest to lowest priority – Treelike structure • Very effective • Chapter 10 Data Structures Using C++ 2 E 49

Application of Queues: Simulation • Queuing systems – Computer simulations • Queues represent the basic data structure – Queues of objects • Waiting to be served by various servers – Consist of servers and queues of objects waiting to be served Data Structures Using C++ 2 E 50

Designing a Queuing System • Server – Object that provides the service • Customer – Object receiving the service • Transaction time (service time) – Time required to serve a customer • Queuing system consists of servers, queue of waiting objects – Model system consisting of a list of servers; waiting queue holding the customers to be served Data Structures Using C++ 2 E 51

Summary • Queue – First In First Out (FIFO) data structure – Implemented as array or linked list – Linked lists: queue never full • Standard Template Library (STL) – Provides a class to implement a queue in a program • Priority Queue – Customers with higher priority pushed to the front • Simulation – Common application for queues Data Structures Using C++ 2 E 52