Data Structures Theorem If a binary tree has

Data Structures

Theorem If a binary tree has n>=2 leaves (n is a finite number), this tree must contain a subtree that has between n/3 and 2 n/3 leaves, inclusive. n Copy and pasted. n

Contradiction If a binary tree has n>=2 leaves (n is a finite number), this tree contains a subtree “s” that has either m<(n/3) or m>(2 n/3) n m is s’s leaves. n

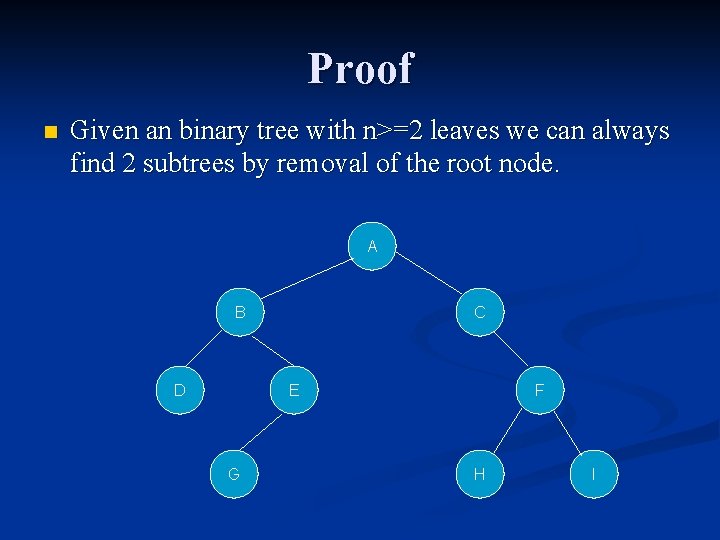
Proof n Given an binary tree with n>=2 leaves we can always find 2 subtrees by removal of the root node. A B D C E G F H I

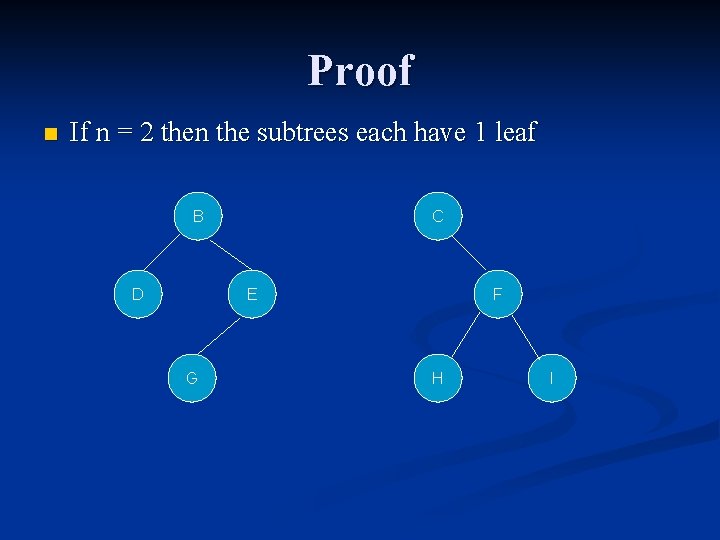
Proof n If n = 2 then the subtrees each have 1 leaf B D C E G F H I

Proof If n=3 s (one subtree) has 1 leaf and s’ (the other subtree) has 2 so in this case these cause the proposition to hold true for n>=3. n Assume the position is false for the sake of contradiction. n

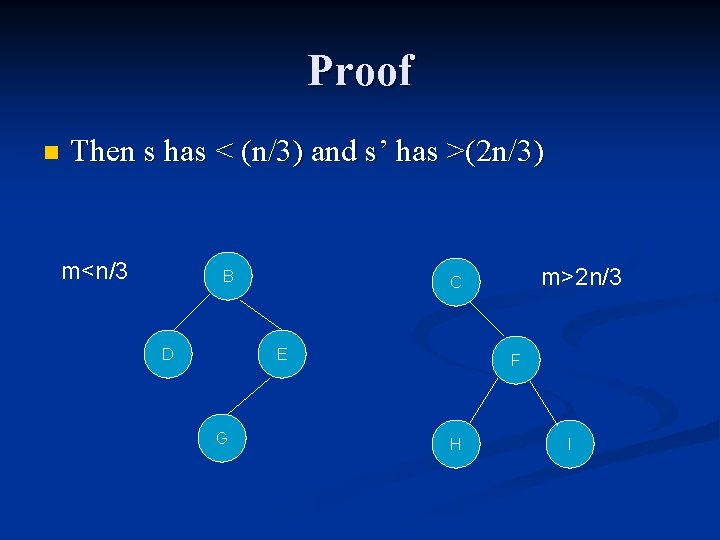
Proof n Then s has < (n/3) and s’ has >(2 n/3) m<n/3 B D E G m>2 n/3 C F H I

Proof If we take the larger of the 2 (whether s or s’) and again remove the top node (like in slide 4) one subtree must still have m>2 n/3 n This is because of the assumption for the sake of contradiction (because one of the 2 subtrees must contain at least ½ the leaves) n The other subtree (s’) must contain at least one leaf (like in slide 5) n

Proof n Repeating the process with the larger subtree (whether it be s or s’) will remove at least 1 leaf and yet leave m>2 n/3 leaves but that can only continue if the tree is infinite. CONTRADICTION!!

The principle of the proof is simple. Proving by contradiction was difficult to show, but easily applied.