Data Structures Selection Haim Kaplan Uri Zwick December
Data Structures Selection Haim Kaplan & Uri Zwick December 2013 1
Selection Given n items, each with a key that belongs to a totally ordered domain, select the item with the k-th largest key The item with the n/2 -th largest key is called the median The k-th largest item is also called the k-th order statistic Can we do it faster than sorting?
![Quick-select ≥ A[k]](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-3.jpg "Quick-select ≥ A[k]")
Quick-select ≥ A[k]
![Quick-select (Adapted from Sedgewick’s Algorithms in Java) ≥ A[k]](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-4.jpg "Quick-select (Adapted from Sedgewick’s Algorithms in Java) ≥ A[k]")
Quick-select (Adapted from Sedgewick’s Algorithms in Java) ≥ A[k]
Fredman’s analysis (2013) The probability that ni+1 ≤ (3/4)ni is at least 1/2 Expected number of comparisons needed to get from ni to first nj with nj ≤(3/4)ni is at most 2 ni Total expected number of comparisons is at most
![Exact analysis [Knuth 1971] P 2 C 2 E (Slightly more complicated than the](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-6.jpg "Exact analysis [Knuth 1971] P 2 C 2 E (Slightly more complicated than the")
Exact analysis [Knuth 1971] P 2 C 2 E (Slightly more complicated than the analysis of quicksort)
Approximate median by sampling Suppose that we only want an item whose rank is close to n/2. (rank = index in sorted order) Choose a random sample of size s Find the median m of the sample With high probability, the rank of m in the original set is in the range 7
![Exact median via sampling [Floyd-Rivest (1975)] Choose a random sample of size n 3/4](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-8.jpg "Exact median via sampling [Floyd-Rivest (1975)] Choose a random sample of size n 3/4")
Exact median via sampling [Floyd-Rivest (1975)] Choose a random sample of size n 3/4 8
![Exact median via sampling [Floyd-Rivest (1975)] 9](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-9.jpg "Exact median via sampling [Floyd-Rivest (1975)] 9")
Exact median via sampling [Floyd-Rivest (1975)] 9
![Exact median via sampling [Floyd-Rivest (1975)] 10](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-10.jpg "Exact median via sampling [Floyd-Rivest (1975)] 10")
Exact median via sampling [Floyd-Rivest (1975)] 10
![Deterministic linear time selection [Blum, Floyd, Pratt, Rivest, and Tarjan (1973)] 11](http://slidetodoc.com/presentation_image_h2/90f3bd567099cff47d909b99831bf188/image-11.jpg "Deterministic linear time selection [Blum, Floyd, Pratt, Rivest, and Tarjan (1973)] 11")
Deterministic linear time selection [Blum, Floyd, Pratt, Rivest, and Tarjan (1973)] 11
Split the items into 5 -tuples 6 2 9 5 1 12
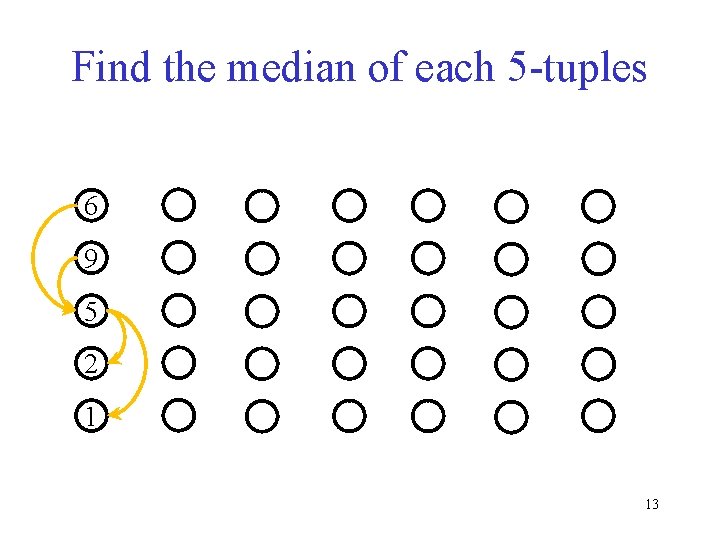
Find the median of each 5 -tuples 6 9 5 2 1 13
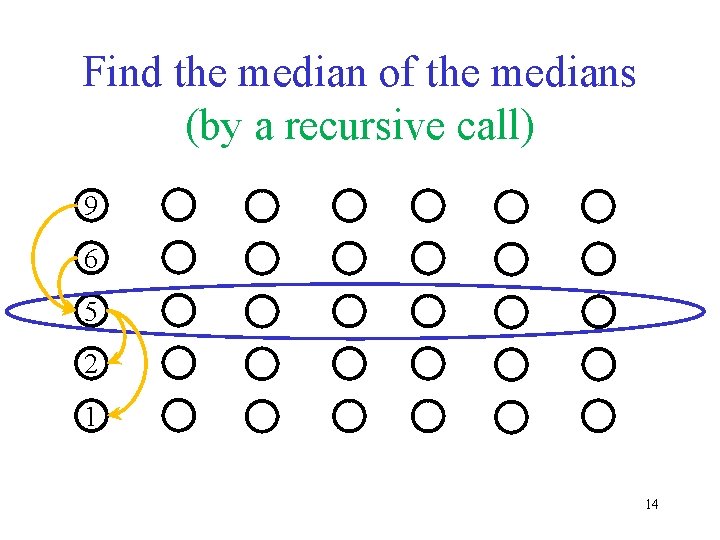
Find the median of the medians (by a recursive call) 9 6 5 2 1 14
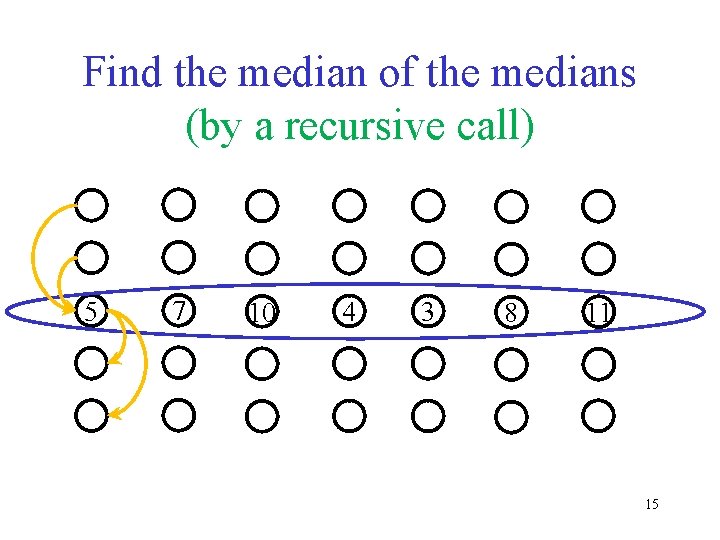
Find the median of the medians (by a recursive call) 5 7 10 4 3 8 11 15
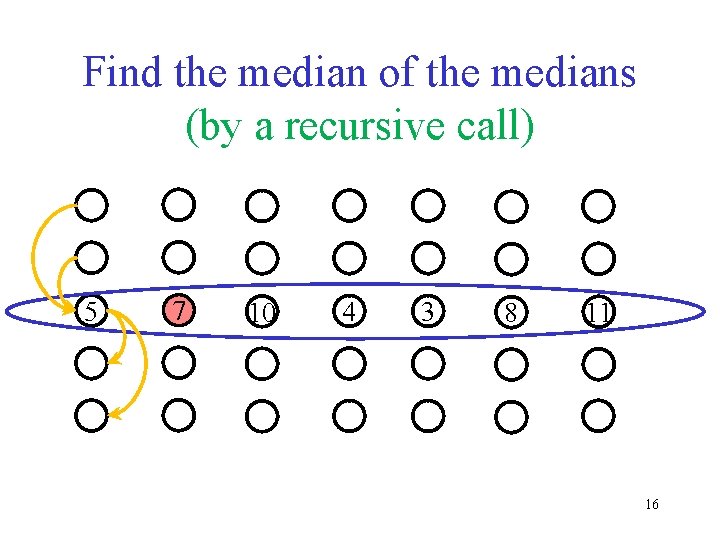
Find the median of the medians (by a recursive call) 5 7 10 4 3 8 11 16
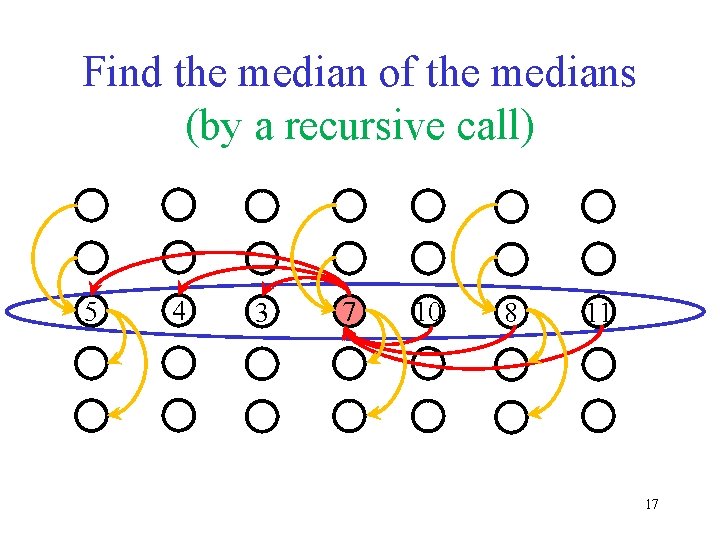
Find the median of the medians (by a recursive call) 5 4 3 7 10 8 11 17
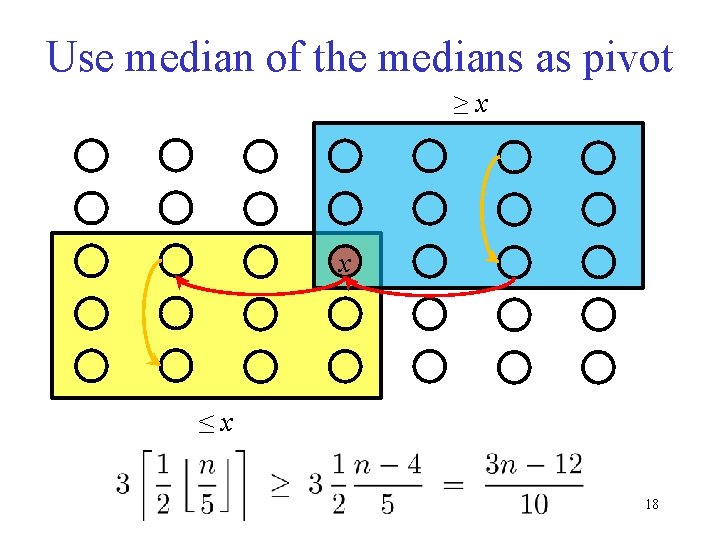
Use median of the medians as pivot ≥x x ≤x 18
Analysis Counting comparisons Induction basis: Easily verified for 2 ≤ n < 10 19
Analysis Counting comparisons Induction step: 20
Some improvements The median of 5 items can be found using 6 comparisons The pivot x should be compared to only 2 items in each 5 -tuple Many other improvements are possible 21
“Master Theorem” for recurrence relations Many generalizations 22
- Slides: 22