Data Structures More List Methods Our first encoding

Data Structures More List Methods Our first encoding Matrix

CQ: Are these programs equivalent? 1 2 b = [‘h’, ’e’, ’l’, ’o’] b. insert(len(b), “w”) print(b) A: yes B: no b = [‘h’, ’e’, ’l’, ’o’] b. append(“w”) print(b)

Advanced List Operations L = [0, 1, 2, 0] L. reverse() print(L) will print: [0, 2, 1, 0] L. remove(0) print(L) will print: [2, 1] print (L. index(2)) will print 0

Why are Lists useful? They provide a mechanism for creating a collection of items def double. List(b): i=0 while i < len(b): b[i] = 2 * b[i] i = i +1 return (b) print(double. List([1, 2, 3]))

Using Lists to Create Our Own Encodings Python provides a number of encodings for us: Binary, ASCII, Unicode, RGB, Pictures etc. We know the basic building blocks, but we are still missing something … We need to be able to create our own encodings What if I want to write a program that operates on proteins?

Under the hood: what is a matrix? A matrix is not “pre defined” in python We “construct” a way to encode a matrix through the use of lists We will see how to do so using a single list (not ideal) We will see how to do so using a list of lists Two different ways Row by Row Column by Column 12 34 ( )

Lists Suppose we wanted to extract the value 3 y = [“ABCD”, [1, 2, 3] , ”CD”, ”D”] y[1][2] The first set of [] get the array in position 1 of y. The second [] is selecting the element in position 2 of that array. This is equiv. to: z = y[1] z[2]

Lets make it more concrete! Lets revisit encoding a matrix Lets try something simple: A = [1, -1, 0, 2] B = [1, 0, 0, 0. 5, 3, 4, -1, -3, 6]

Does this work? We lose a bit of information in this encoding Which numbers correspond to which row We can explicitly keep track of rows through a row length variable B = [1, 0, 0, 0. 5, 3, 4, -1, -3, 6] row. Length = 3 B[row. Length*y +x]

Lets convince ourselves B = [1, 0, 0, 0. 5, 3, 4, -1, -3, 6] row. Length = 3 B[row. Length*y +x] x=0 y=0 B[3*0 + 0] x=1 y=1 B[3*1 + 1] x=2 y=1 B[3*1 + 2]

Can we encode it another way? We can encode column by column, but we lose some information again Which numbers correspond to which column We can explicitly keep track of columns through a column length variable B = [1, 0. 5, -1, 0, 3, -3, 0, 4, 6] column. Length = 3 B[column. Length*x + y]

Lets convince ourselves B = [1, 0. 5, -1, 0, 3, -3, 0, 4, 6] column. Length = 3 B[column. Length*x + y] x=0 y=0 B[3*0 + 0] x=1 y=1 B[3*1 + 1] x=2 y=1 B[3*2 + 1]

Lists of Lists Recall that when we had a string in our list B = [“ABCD”, 0, 1, 3] We could utilize the bracket syntax multiple times print B[0][1] would print B Lists can store other Lists B = [[0, 1, 3], 4, 5, 6]

Another way to encode a Matrix Lets take a look at our example matrix What about this? B= [[1, 0, 0], [0. 5, 3, 4], [-1, -3, 6]]

Why is this important? We can now write code that more closely resembles mathematical notation i. e. , we can use x and y to index into our matrix B = [[1, 0, 0], [0. 5, 3, 4], [-1, -3, 6]] for x in range(3): for y in range(3): print (B[x][y])

…but first some more notation We can use the “*” to create a multi element sequence 6 * [0] results in a sequence of 6 0’s [0, 0, 0, 0] 3 * [0, 0] results in a sequence of 6 0’s [0, 0, 0, 0] 10 * [0, 1, 2] results in what?

What is going on under the hood? Lets leverage some algebraic properties 3 * [0, 0] is another way to write [0, 0] + [0, 0] We know that “+” concatenates two sequences together

What about lists of lists? We have another syntax for creating lists [ X for i in range(y)] This creates a list with y elements of X Example: [ 0 for i in range(6)] ≡ [0]*6 [0, 0 , 0 , 0] Example: [[0, 0] for i in range(3)] ≡ [[0, 0]]*3 [[0, 0], [0, 0]] What does this does: [2*[0] for i in range(3)]?

Lets put it all together m 1 = [ [1, 2, 3, 0], [4, 5, 6, 0], [7, 8, 9, 0] ] m 2 = [ [2, 4, 6, 0], [1, 3, 5, 0], [0, -1, -2, 0] ] m 3= [ 4*[0] for i in range(3) ] for x in range(3): for y in range(4): m 3[x][y]= m 1[x][y]+m 2[x][y]

Data structures We have constructed our first data structure! As the name implies, we have given structure to the data The data corresponds to the elements in the matrix The structure is a list of lists The structure allows us to utilize math-like notation

Clicker Question: did we encode the same matrix in both programs? 1 2 [[1, 2], [3, 4]] [[1, 3], [2, 4]] A: yes B: no C: maybe

Lets explore why it depends 1 [[1, 2], [3, 4]] 12 34 ( ) 2 [[1, 3], [2, 4]] 13 24 ( ) Both lists of lists can either be a row by row or a column by column encoding

Let us encode something else using lists!

We call this structure a tree Root

How might we encode such a structure? What structures do we know of in python? Strings, Ranges, Lists We know that lists allow us to encode complex structures via sub lists We used sub list to encode either a row or a column in the matrix We used an ‘outer’ list of rows or columns as a matrix

Can we use the same strategy? How might we encode a simple tree? Root Leaf 1 Leaf 2 Leaf 3 Tree = [‘Leaf 1’, ‘Leaf 2’, ‘Leaf 3’]

Trees can be more complex Root Leaf 1 Leaf 2 Leaf 3 Leaf 4 Leaf 5 Tree = [‘Leaf 1’, ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, ‘Leaf 5’]]

Trees can be more complex Root Leaf 2 Leaf 0 Leaf 1 Leaf 3 Leaf 4 Leaf 5 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, ‘Leaf 5’]]

Trees can be more complex Root Leaf 2 Leaf 0 Leaf 1 Leaf 3 Leaf 4 Leaf 5 Leaf 6 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]]

What is the intuition Each sub list encodes the ‘branches’ of the tree We can think of each sub list as a ‘sub tree’ We can use indexes (the bracket notation []) to select out elements or ‘sub trees’

How can we select out the leaves? Root Leaf 1 Leaf 2 Leaf 3 Tree[0] Tree[1] Tree[2] Tree = [‘Leaf 1’, ‘Leaf 2’, ‘Leaf 3’]

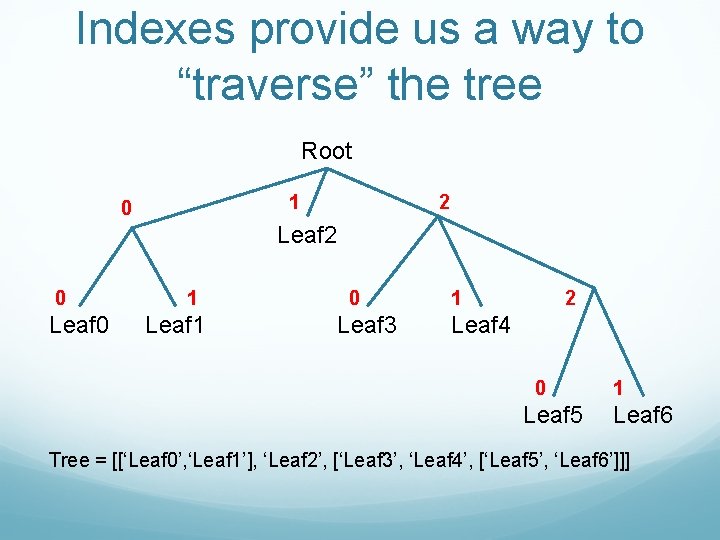
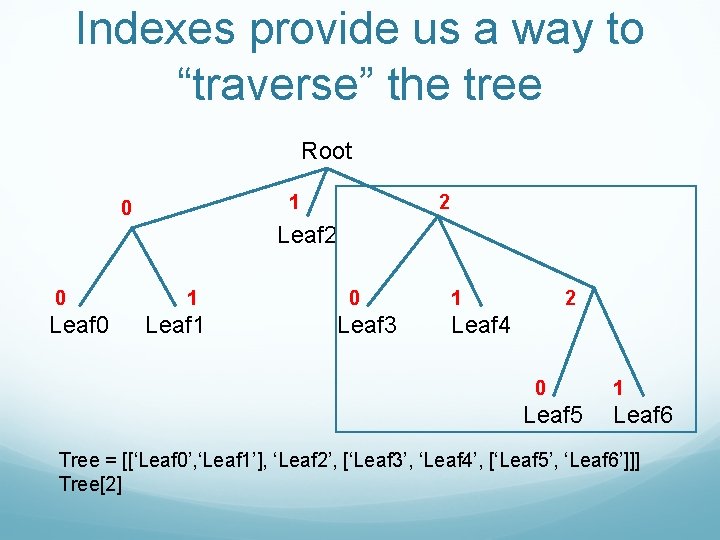
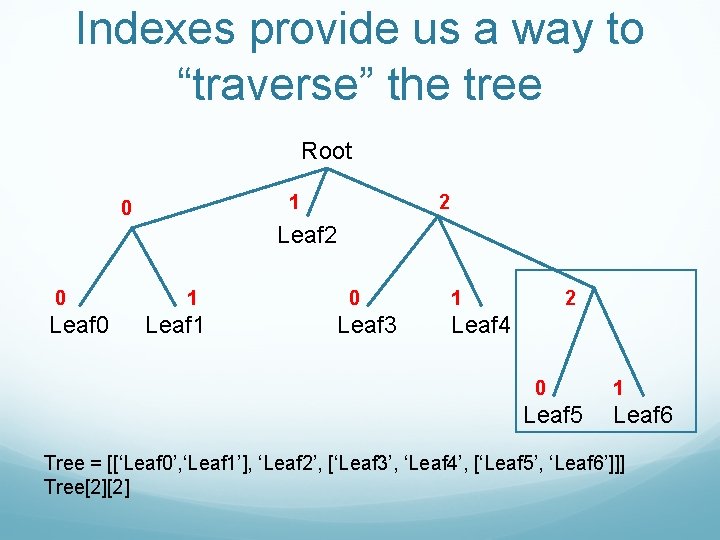
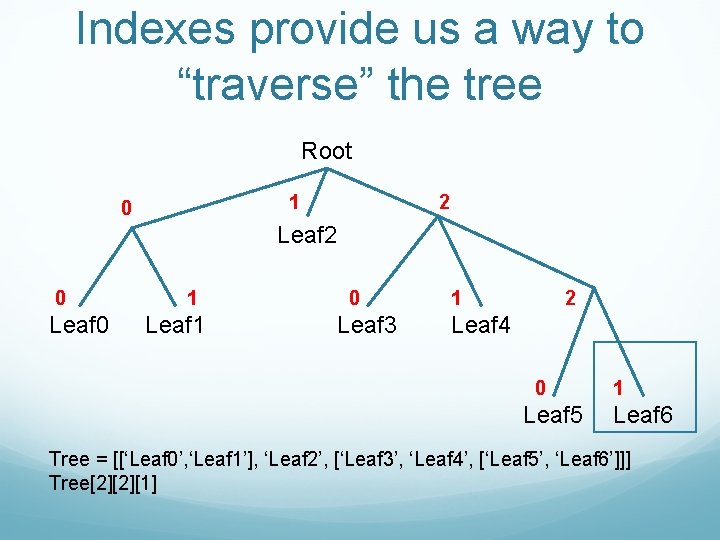
Indexes provide us a way to “traverse” the tree Root 1 0 2 Leaf 2 0 Leaf 0 1 Leaf 1 0 Leaf 3 1 2 Leaf 4 0 Leaf 5 1 Leaf 6 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]]

Indexes provide us a way to “traverse” the tree Root 1 0 2 Leaf 2 0 Leaf 0 1 Leaf 1 0 Leaf 3 1 2 Leaf 4 0 Leaf 5 1 Leaf 6 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] Tree[2]

Indexes provide us a way to “traverse” the tree Root 1 0 2 Leaf 2 0 Leaf 0 1 Leaf 1 0 Leaf 3 1 2 Leaf 4 0 Leaf 5 1 Leaf 6 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] Tree[2][2]

Indexes provide us a way to “traverse” the tree Root 1 0 2 Leaf 2 0 Leaf 0 1 Leaf 1 0 Leaf 3 1 2 Leaf 4 0 Leaf 5 1 Leaf 6 Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] Tree[2][2][1]

CQ: How do we select ‘Leaf 4’ from the Tree? Tree = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’, [‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] A: Tree[2][1] B: Tree[3][2] C: Tree[1][2]

Operations on Trees, since they are encoded via lists support the same operations lists support We can “+” two trees We can embedded two trees within a list This creates a larger tree with each of the smaller trees as sub trees Example: Tree 1 = [‘Leaf 1’, ‘Leaf 2’] Tree 2 = [‘Leaf 3’, ‘Leaf 4’] Tree = [Tree 1, Tree 2]

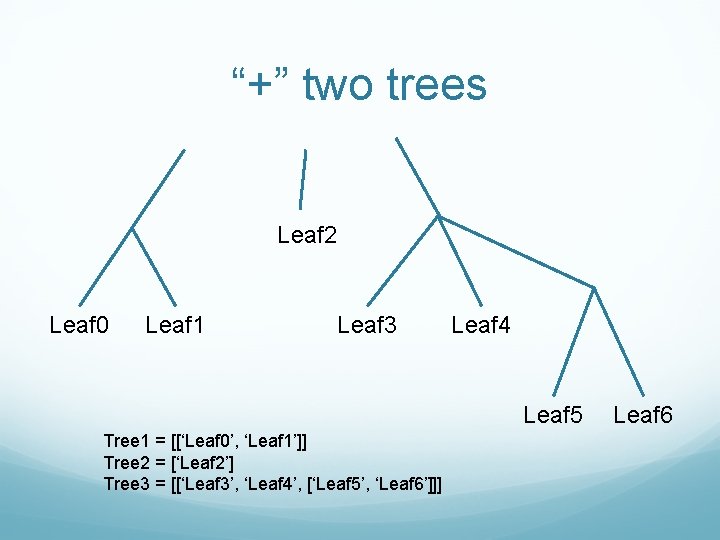
“+” two trees Leaf 2 Leaf 0 Leaf 1 Leaf 3 Leaf 4 Leaf 5 Tree 1 = [[‘Leaf 0’, ‘Leaf 1’]] Tree 2 = [‘Leaf 2’] Tree 3 = [[‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] Leaf 6

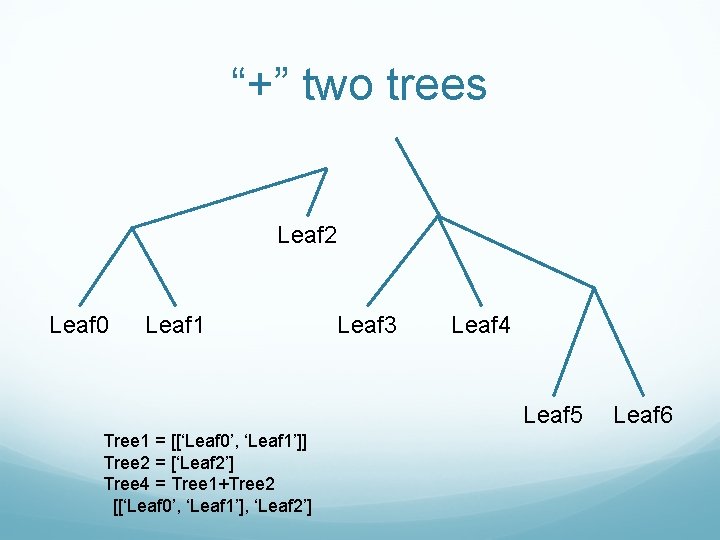
“+” two trees Leaf 2 Leaf 0 Leaf 1 Leaf 3 Leaf 4 Leaf 5 Tree 1 = [[‘Leaf 0’, ‘Leaf 1’]] Tree 2 = [‘Leaf 2’] Tree 4 = Tree 1+Tree 2 [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’] Leaf 6

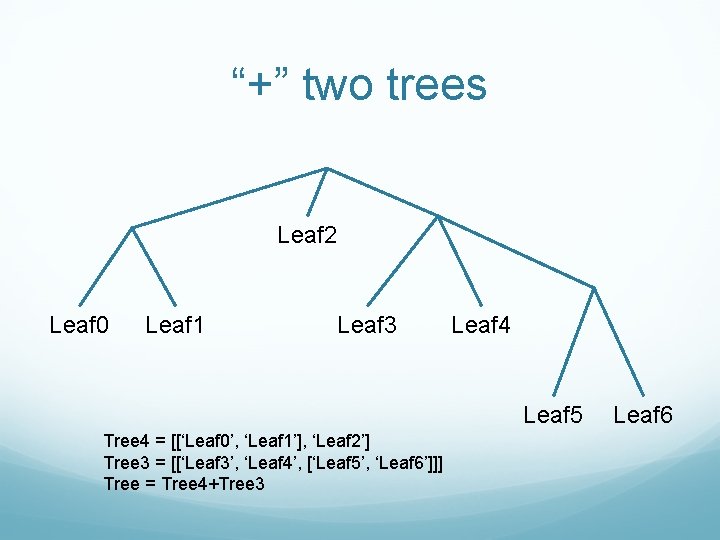
“+” two trees Leaf 2 Leaf 0 Leaf 1 Leaf 3 Leaf 4 Leaf 5 Tree 4 = [[‘Leaf 0’, ‘Leaf 1’], ‘Leaf 2’] Tree 3 = [[‘Leaf 3’, ‘Leaf 4’, [‘Leaf 5’, ‘Leaf 6’]]] Tree = Tree 4+Tree 3 Leaf 6

Why are trees important? They are a fundamental structure in computer science They enable us to search very quickly We will revisit trees later in the course What have we covered so far: Given a tree diagram we can write a list of lists Given a complex list we can select elements