Data Structures Lecture No 03 Queues A stack

Data Structures Lecture No. 03

Queues § A stack is LIFO (Last-In First Out) structure. § In contrast, a queue is a FIFO (First-In First-Out ) structure. § A queue is a linear structure for which items can be only enqueed at one end and removed at another end.

Queues In Everyday Life

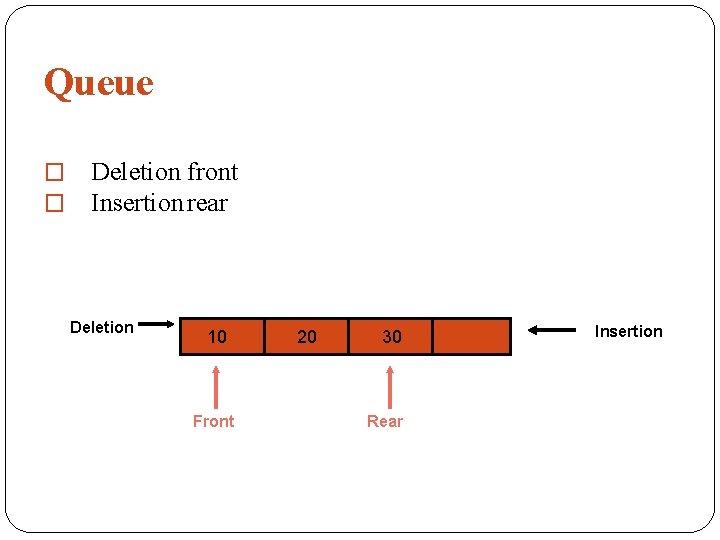
Queue � � Deletion front Insertion rear Deletion 10 Front 20 30 Rear Insertion

Queue � The terms “front” and “rear” are used in describing a queue

Queue Operations enqueue(X) – place X at the rear of the queue. dequeue() -- remove the front element and return it. front() -- return front element without removing it. Is. Empty() --return TRUE if queue is empty, FALSE otherwise

Representation Of Queues may be represented as � 1. 2. One-way linked-list Linear array Linear Array 2. • • • Consider a linear array QUEUE and two pointer variables FRONT and REAR FRONT location of front element REAR location of rear element

Representation Of Queues Linear Array 2. • • FRONT=REAR=NULL queue empty If array QUEUE has N elements then � When new element added REAR: = REAR+1 � When an element deleted FRONT: = FRONT+1 � After N insertions REAR will occupy QUEUE[N]

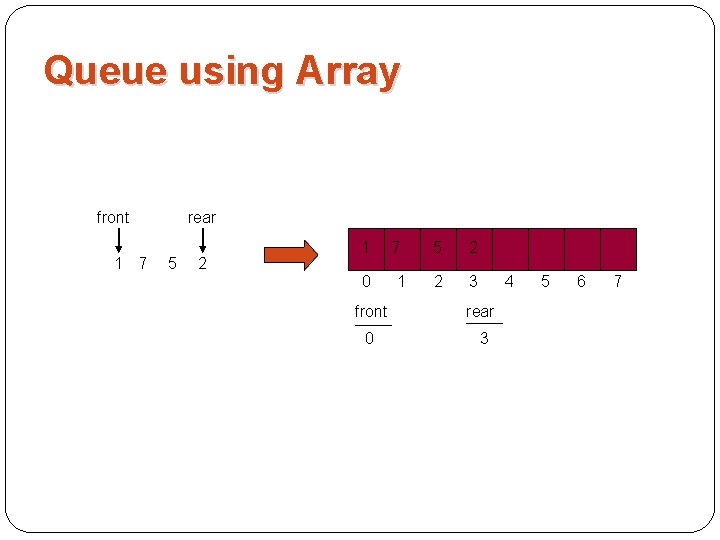
Queue using Array front 1 7 rear 5 2 1 0 7 1 5 2 2 3 4 front rear 0 3 5 6 7

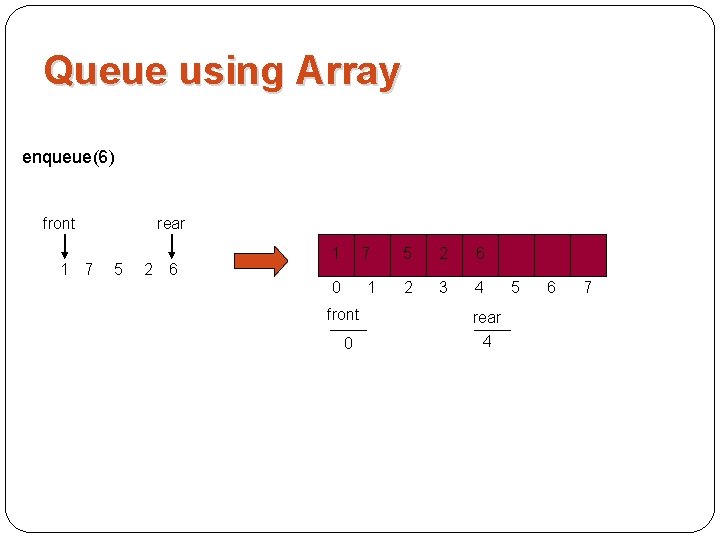
Queue using Array enqueue(6) front 1 7 rear 5 2 6 1 7 0 1 front 0 5 2 6 2 3 4 rear 4 5 6 7

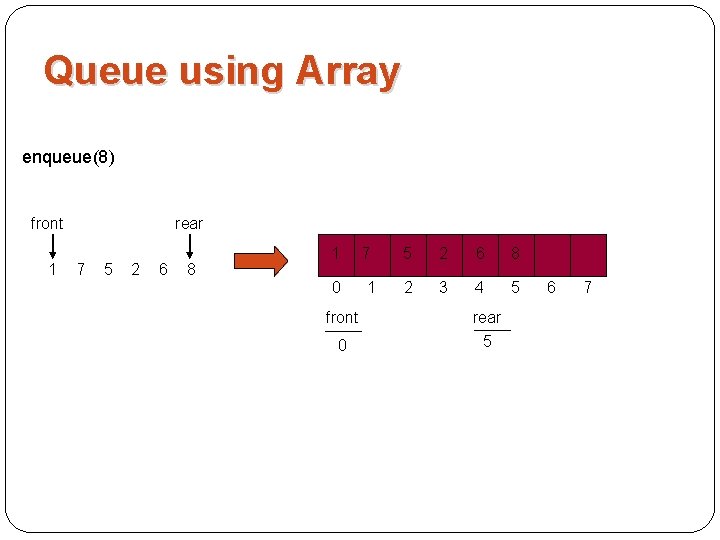
Queue using Array enqueue(8) front 1 rear 7 5 2 6 8 1 0 front 0 7 1 5 2 6 8 2 3 4 5 rear 5 6 7

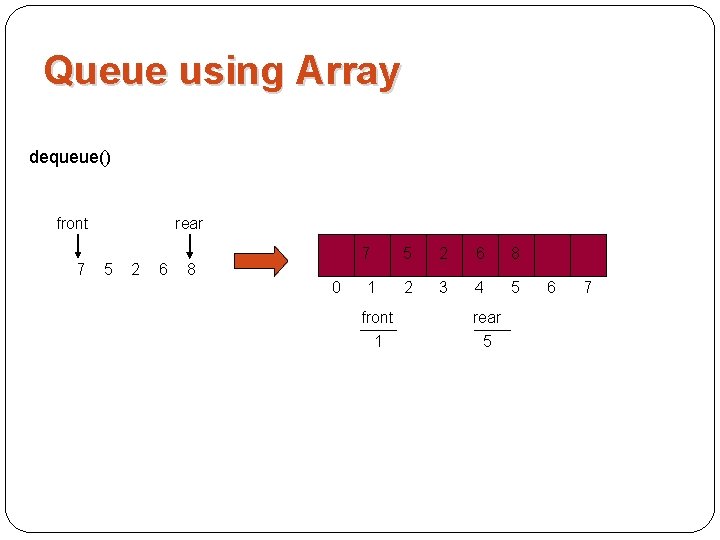
Queue using Array dequeue() front 7 rear 5 2 6 7 8 0 1 front 1 5 2 6 8 2 3 4 5 rear 5 6 7

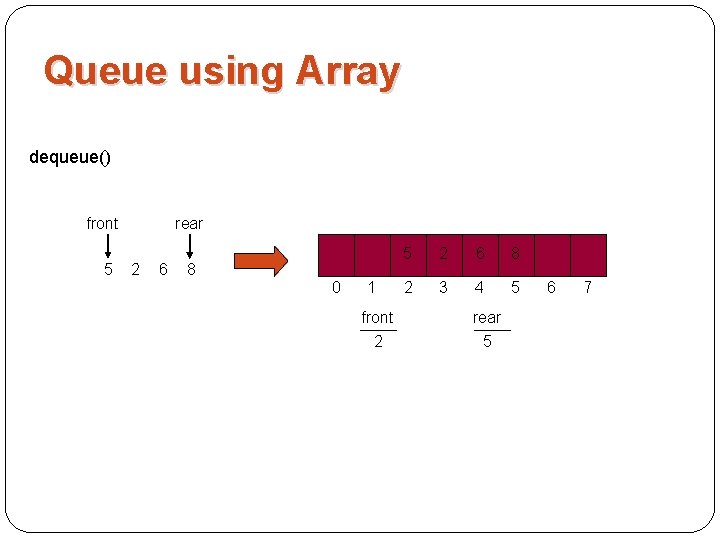
Queue using Array dequeue() front 5 rear 2 6 8 0 1 front 2 5 2 6 8 2 3 4 5 rear 5 6 7

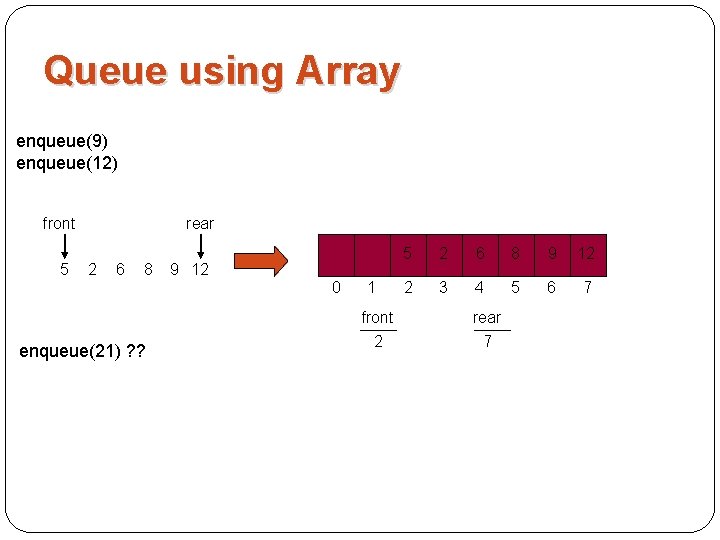
Queue using Array enqueue(9) enqueue(12) front 5 rear 2 6 8 9 12 0 enqueue(21) ? ? 1 front 2 5 2 6 8 9 12 2 3 4 5 6 7 rear 7

QINSERT(QUEUE, N, FRONT, REAR, ITEM) � This algorithm is used to insert an ITEM into a queue. 1. [Queue already filled? ] If (REAR=N) then Write: Overflow, and Return. 2. [Set the Rear Pointer] REAR: =REAR+1 3. [Insert the Item in the Queue] QUEUE[REAR]=ITEM 4. [Is the front Pointer set? ] if front=0 then set front = 1 5. [Finish] [exit]

QDELETE � 1. 2. 3. 4. QDELETE(QUEUE, N, FRONT, REAR, ITEM) This algorithm is used to delete an ITEM from a queue and assigns it to the variable ITEM. [Queue already empty? ] If FRONT: =NULL, then Write: Underflow, and Return. [Delete Item] Set ITEM: = QUEUE[FRONT] [Set FRONT Pointer] If (FRONT: = REAR), then: [Queue has only one element] FRONT: = NULL REAR: = NULL Else FRONT: =FRONT+1 [End of If structure. ] [finish] exit.

Program of Queue. . #include<iostream> #include<conio. h> #define MAX 10 void enque(); void display(); void deque(); int que 1[MAX], front=-1, rear=-1, item; void main() { enque(); display(); deque(); display(); getch(); }

enque() in queue. . void enque() { if(rear==(MAX-1)) cout<<"n Queue is Already Full. . "; else { cout<<"n. Enter an Item in Queue. . "; cin>>item; if(rear==-1 && front==-1) {rear++; front++; } else rear++; que 1[rear]=item; }}

display() in queue void display() { int i; if(front==-1) cout<<"n Queue is Alreday Empty. . . "; else { cout<<"n Items is in the Queue. . . "; for(i=front; i<=rear; i++) cout<<que 1[i]<<"t"; } }

delete() in queue void deque() { int x; if(front==-1) cout<<"n. Queue is Already Empty. . "; else { if(rear==front) {rear=-1; front=-1} else front++; x=que 1[front]; cout<<"n. Deleting item from queue is "<<x; } }

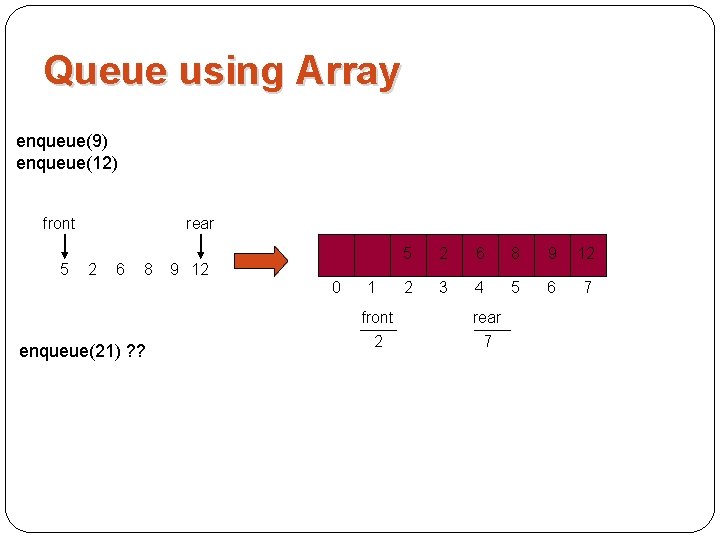
Queue using Array § Cannot insert new elements even though there are two places available at the start of the array. § Solution: allow the queue to “wrap around”.

Queue using Array enqueue(9) enqueue(12) front 5 rear 2 6 8 9 12 0 enqueue(21) ? ? 1 front 2 5 2 6 8 9 12 2 3 4 5 6 7 rear 7

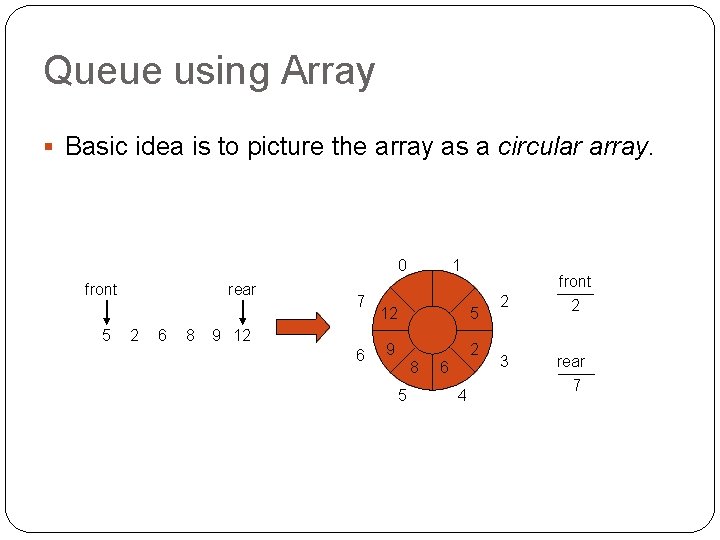
Queue using Array § Basic idea is to picture the array as a circular array. 0 front 5 rear 2 6 8 7 9 12 6 1 12 5 9 2 8 5 6 4 2 3 front 2 rear 7

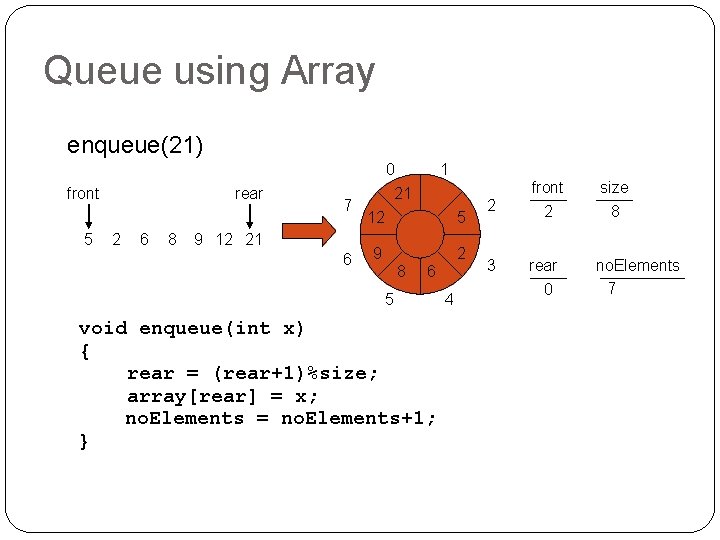
Queue using Array enqueue(21) front 5 rear 2 6 8 7 9 12 21 6 0 21 1 12 5 9 2 8 6 5 void enqueue(int x) { rear = (rear+1)%size; array[rear] = x; no. Elements = no. Elements+1; } 4 2 front 2 size 8 3 rear no. Elements 7 0

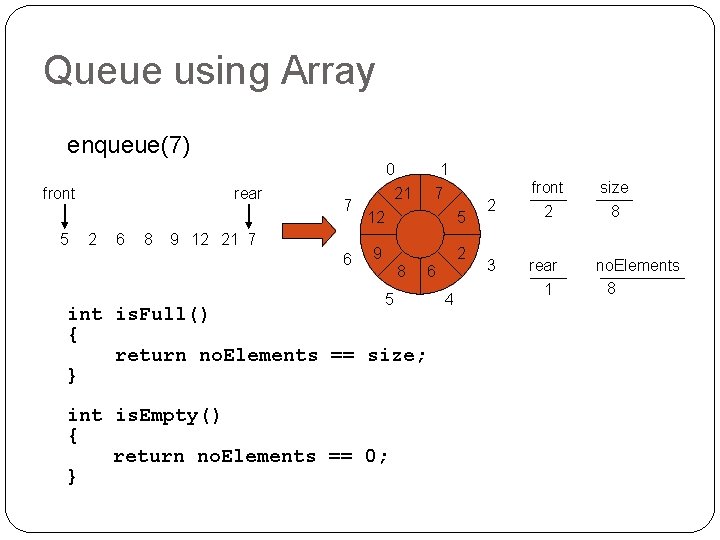
Queue using Array enqueue(7) front 5 rear 2 6 8 7 9 12 21 7 6 0 21 1 7 12 5 9 2 8 5 int is. Full() { return no. Elements == size; } int is. Empty() { return no. Elements == 0; } 6 4 2 front 2 size 8 3 rear no. Elements 8 1

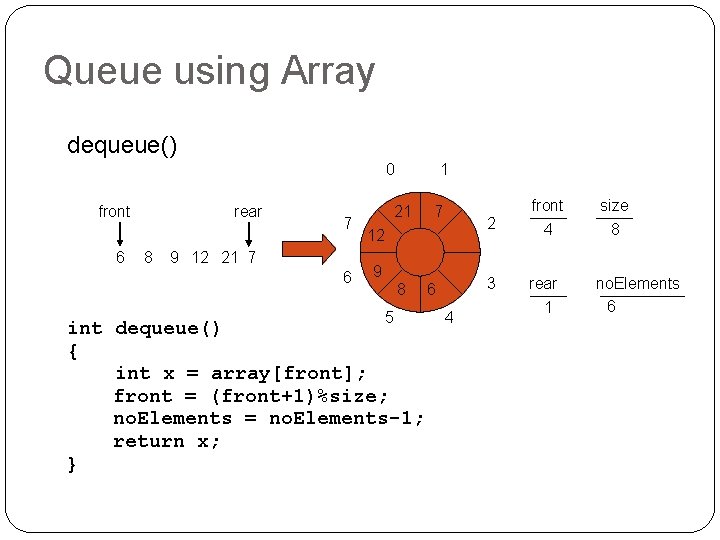
Queue using Array dequeue() 0 front 6 rear 8 7 9 12 21 7 6 1 21 7 2 12 9 8 5 int dequeue() { int x = array[front]; front = (front+1)%size; no. Elements = no. Elements-1; return x; } 3 6 4 front 4 size 8 rear 1 no. Elements 6