Data Structures Graph Graphs are simply a collection

Data Structures - Graph • Graphs are simply a collection of nodes (points) and edges connecting the nodes. • Typical notation lookslike this G = { N, E }. – G = the graph. – N = node set – E = edge set • Nodes represent items under consideration - can be anything. • Edges represent relationships between the items - can be anything. – Edges can be undirected, meaning the relationship holds both ways between nodes. – Edges can be directed, meaning the relationship is only one way.

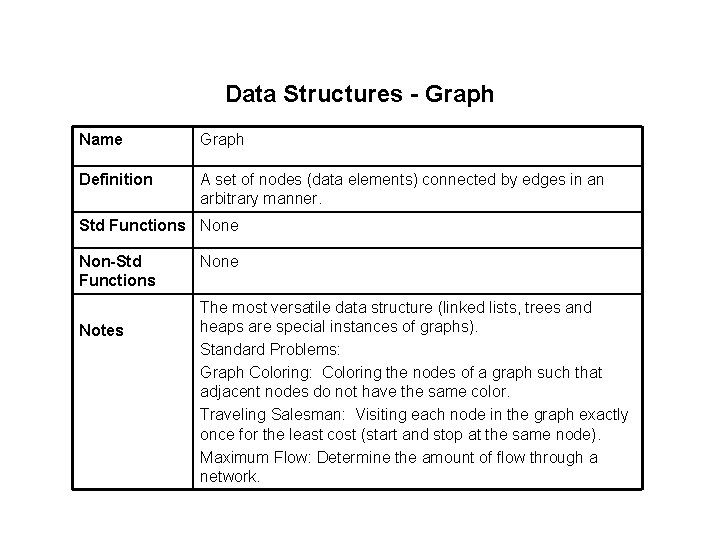
Data Structures - Graph Name Graph Definition A set of nodes (data elements) connected by edges in an arbitrary manner. Std Functions None Non-Std Functions Notes None The most versatile data structure (linked lists, trees and heaps are special instances of graphs). Standard Problems: Graph Coloring: Coloring the nodes of a graph such that adjacent nodes do not have the same color. Traveling Salesman: Visiting each node in the graph exactly once for the least cost (start and stop at the same node). Maximum Flow: Determine the amount of flow through a network.

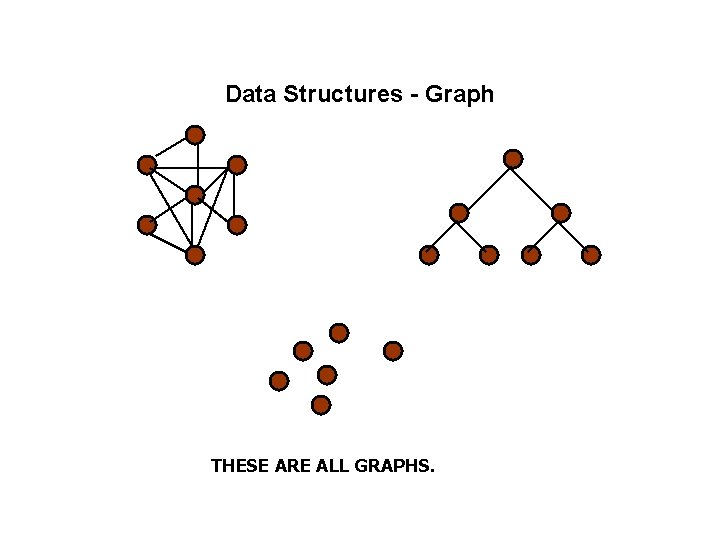
Data Structures - Graph THESE ARE ALL GRAPHS.

Graph Problems • There are literally thousands of graph problems, but we will focus on three that are occur very commonly and show the diversity of the graph structure: – The Traveling Salesman Problem. – Graph Coloring Problem. – Maximum Flow Problem. • At least one of these problems is solved by you every day without you realizing it (until now). • The fact that the nodes and edges can represent anything means that the graph structure is very versatile and virtually any problem can be mapped to a graph problem.

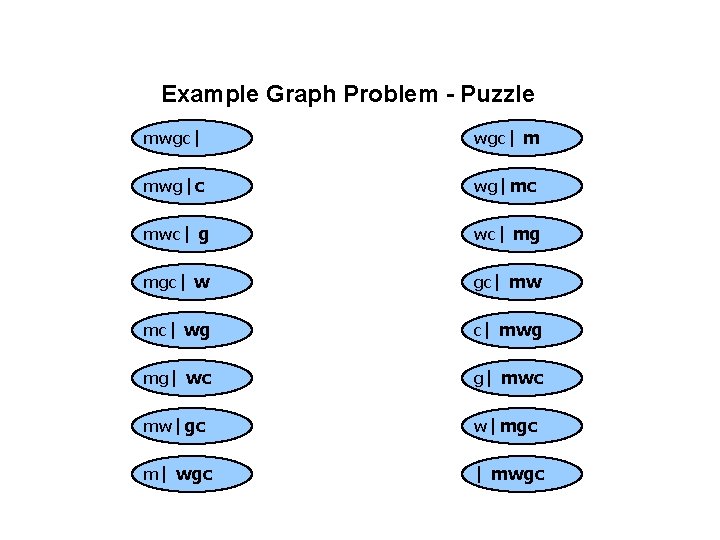
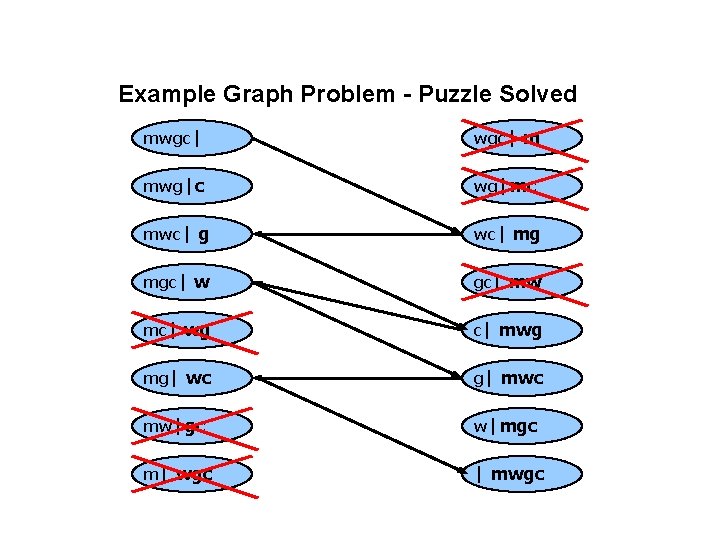
Example Graph Problem - Puzzle • This is an old puzzle and has many variants: A man is returning home from market with a wolf, bag of corn, and goose. He has to cross a lttle river on the way and the only way is to use a little boat. The boats holds him and one other item. – He cannot leave the wolf and goose alone, as the wolf eats the goose. – He cannot leave the corn and goose alone as the goose eats the corn. – He can leave the corn and wolf alone. • How does he get everything across the river and bring everything home (uneaten)? • Build a graph: – N = the set of possible arrangements of man, wolf, goose, corn, and river. – E = Possible transitions due to one boat trip.

Example Graph Problem - Puzzle mwgc| m mwg|c wg|mc mwc| g wc| mg mgc| w gc| mw mc| wg c| mwg mg| wc g| mwc mw|gc w|mgc m| wgc | mwgc

Example Graph Problem - Puzzle Solved mwgc| m mwg|c wg|mc mwc| g wc| mg mgc| w gc| mw mc| wg c| mwg mg| wc g| mwc mw|gc w|mgc m| wgc | mwgc

Graph Problems • There are literally thousands of graph problems, but we will focus on three that are occur very commonly and show the diversity of the graph structure: – The Traveling Salesman Problem. – Graph Coloring Problem. – Maximum Flow Problem. • Each problem has a decision form and an optimization form. The decision form asks "Can we do it? " and the optimization form asks "How well can we do it? " • At least one of these problems is solved by you every day without you realizing it (until now). • The fact that the nodes and edges can represent anything means that the graph structure is very versatile and virtually any problem can be mapped to a graph problem.

Graph Problems - Traveling Salesman • Description: Given a graph, G = {N, E}, where – N = a set of cities. – E = travel routes between the cities, each having a cost associated with it. – One special node, s. – You must begin at city sand travel to each of the other cities exactly once and then return to city s. Thus you make a complete cycle of all cities in the graph. • Decision form of the problem: Can a route be found where the total cost of the trip is less than X? (Answer is yes or no). • Optimization form of the problem: What is the absolute lowest cost?

Graph Problems - Graph Coloring • Description: Given a graph, G = {N, E}, where – N = a set of nodes. – E = edges between the nodes. – The object is to color the graph such that no nodes connecte by an edge have the same color. • Decision form of the problem: Can the graph be colored with X or less colors? (Answer is yes or no). • Optimization form of the problem: What is the fewest number of colors required to color the graph?

Graph Problems - Maximum Flow • Description: Given a graph, G = {N, E}, where – N = a set of nodes. – E = edges representing pipes, each assigned a given capacity. – Two special nodes. Node s is a source node that can potentially spit out an infinite amount of material. Node f is a sink node that can potentially absorb an infinite amount of material. – The object is to determine the maximum amount of material that can flow through the network for the source to the sink. • Decision form of the problem: Can X amount of material be pushed through the network from the source to the sink? (Answer is yes or no). • Optimization form of the problem: What is the maximum amount of material that can flow through the material from the source to the sink?

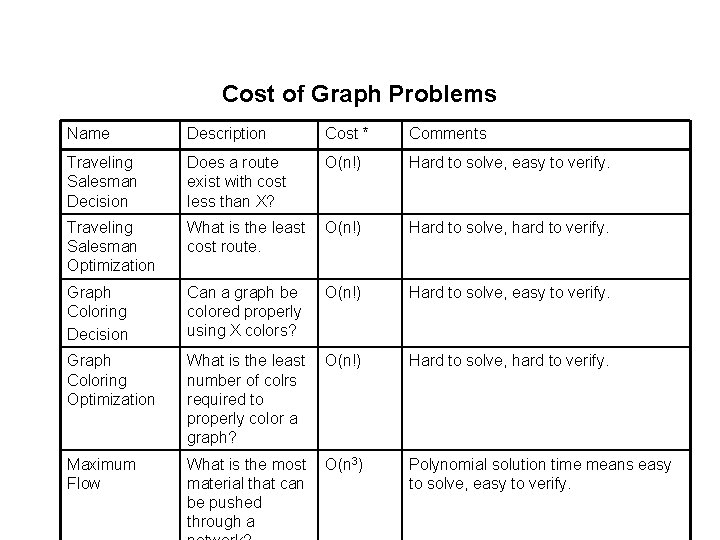
Cost of Graph Problems Name Description Cost * Comments Traveling Salesman Decision Does a route exist with cost less than X? O(n!) Hard to solve, easy to verify. Traveling Salesman Optimization What is the least cost route. O(n!) Hard to solve, hard to verify. Graph Coloring Decision Can a graph be colored properly using X colors? O(n!) Hard to solve, easy to verify. Graph Coloring Optimization What is the least number of colrs required to properly color a graph? O(n!) Hard to solve, hard to verify. Maximum Flow What is the most material that can be pushed through a O(n 3) Polynomial solution time means easy to solve, easy to verify.

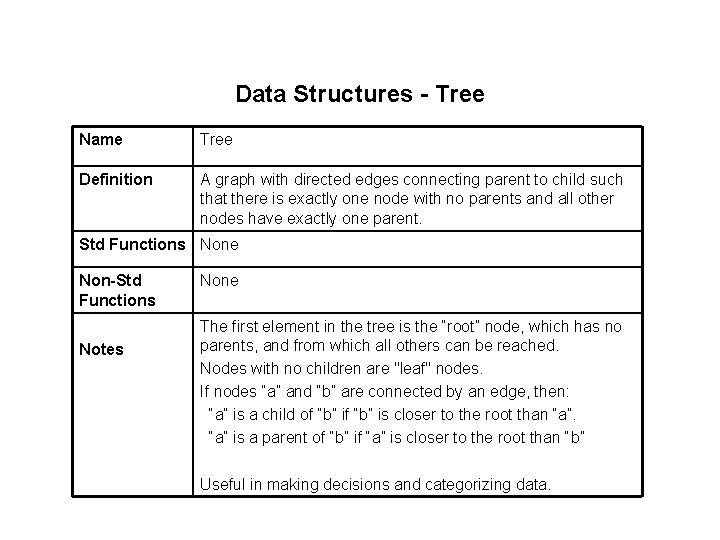
Data Structures - Tree Name Tree Definition A graph with directed edges connecting parent to child such that there is exactly one node with no parents and all other nodes have exactly one parent. Std Functions None Non-Std Functions Notes None The first element in the tree is the “root” node, which has no parents, and from which all others can be reached. Nodes with no children are "leaf" nodes. If nodes “a” and “b” are connected by an edge, then: “a” is a child of “b” is closer to the root than “a” is a parent of “b” if “a” is closer to the root than “b” Useful in making decisions and categorizing data.

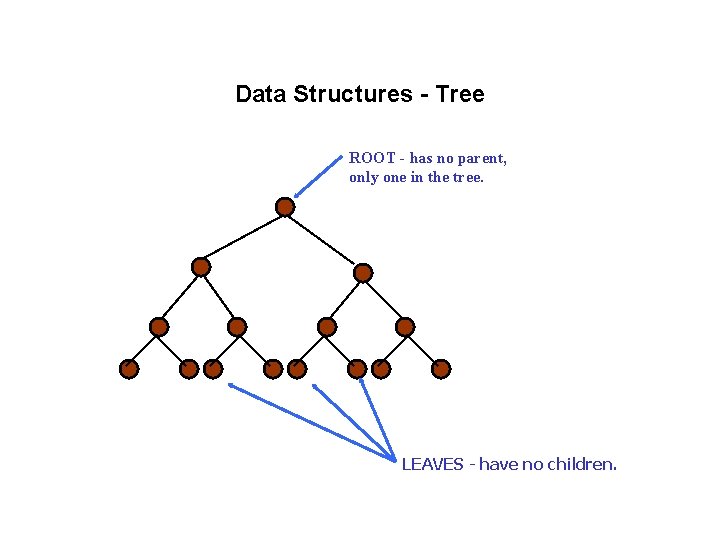
Data Structures - Tree ROOT - has no parent, only one in the tree. LEAVES - have no children.

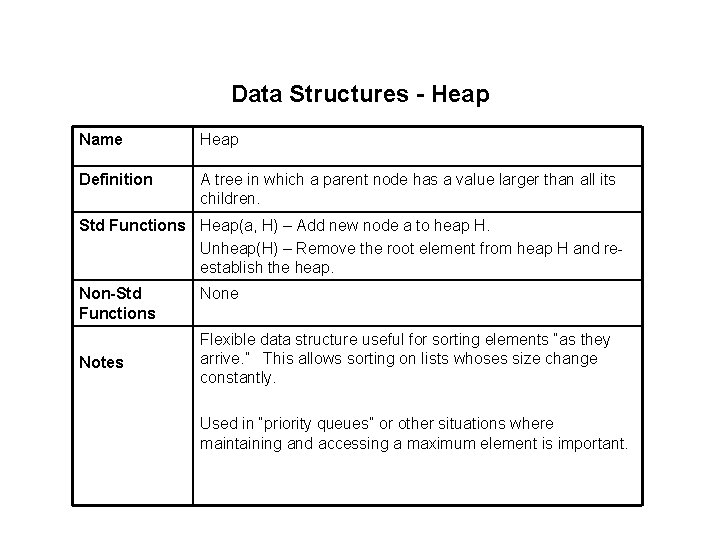
Data Structures - Heap Name Heap Definition A tree in which a parent node has a value larger than all its children. Std Functions Heap(a, H) – Add new node a to heap H. Unheap(H) – Remove the root element from heap H and reestablish the heap. Non-Std Functions Notes None Flexible data structure useful for sorting elements “as they arrive. ” This allows sorting on lists whoses size change constantly. Used in “priority queues” or other situations where maintaining and accessing a maximum element is important.

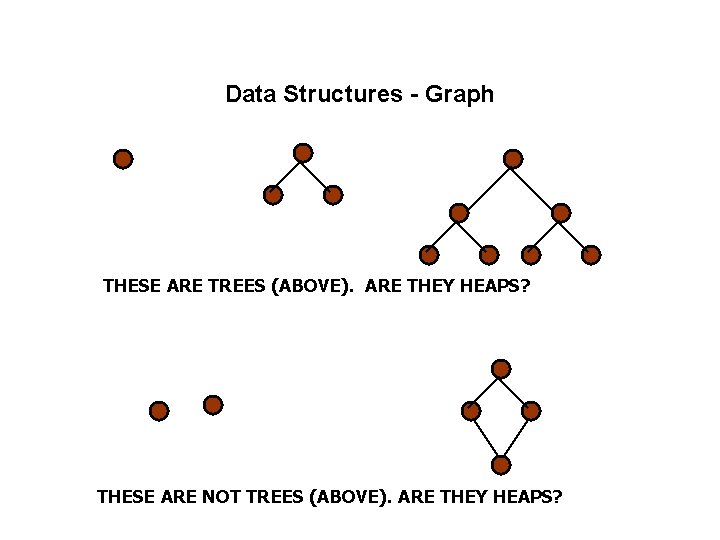
Data Structures - Graph THESE ARE TREES (ABOVE). ARE THEY HEAPS? THESE ARE NOT TREES (ABOVE). ARE THEY HEAPS?