Data Structures Graph 6 1 The Graph Abstract

Data Structures Graph 6. 1 The Graph Abstract Data Type 6. 2 Elementary Graph Operations 6. 3 Minimum Cost Spanning Trees 6. 4 Shortest Path Algorithm

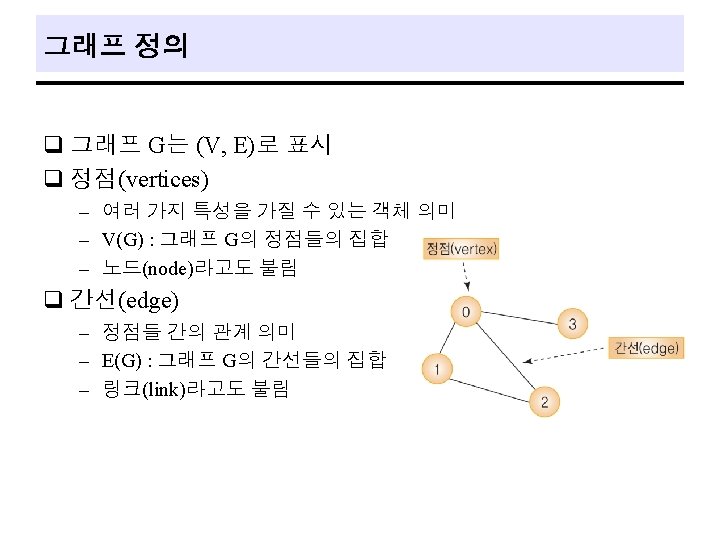
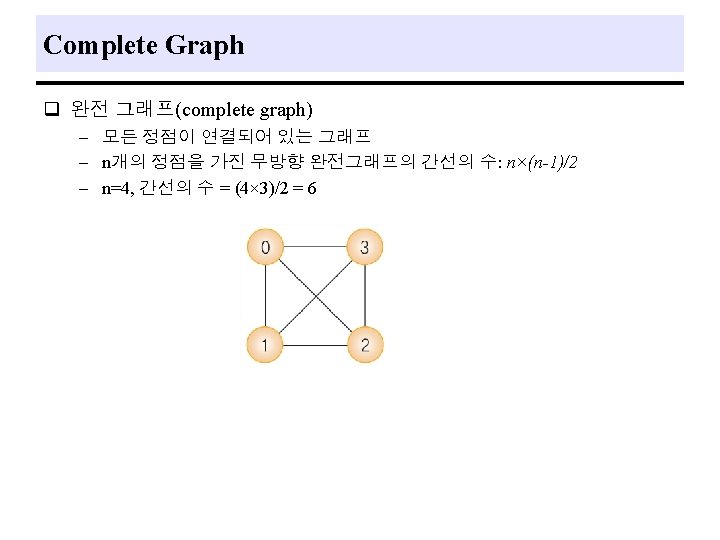
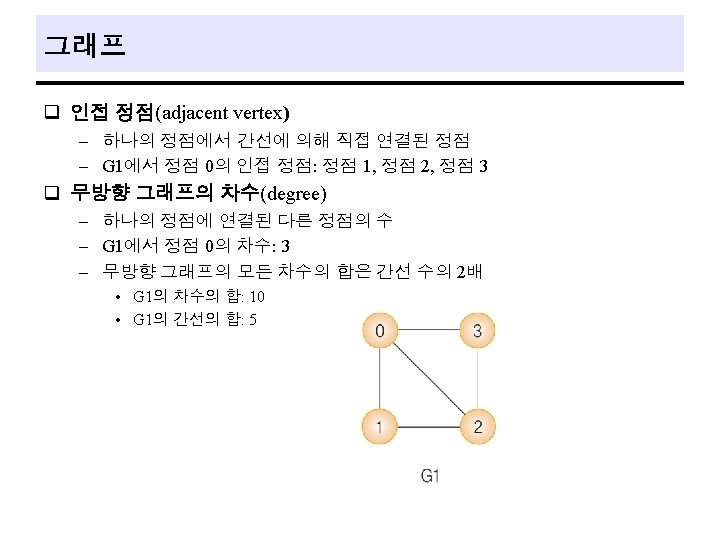
The Graph Abstract Data Type q A graph, G, consists of two sets : a finite, nonempty set of vertices, and a finite, possibly empty set of edges. - V(G) and E(G) represent the sets of vertices and edges of G, respectively. Alternately, we may write G = (V, E) to represent a graph. q Undirected graph is one in which the pair of vertices representing any edge is unordered. - (v 0, v 1), (v 1, v 0) represent the same edge. q Directed graph is one in which we represent each edge as a directed pair of vertices. - <v 0, v 1> represents an edge in which v 0 is the tail and v 1 is the head. 6

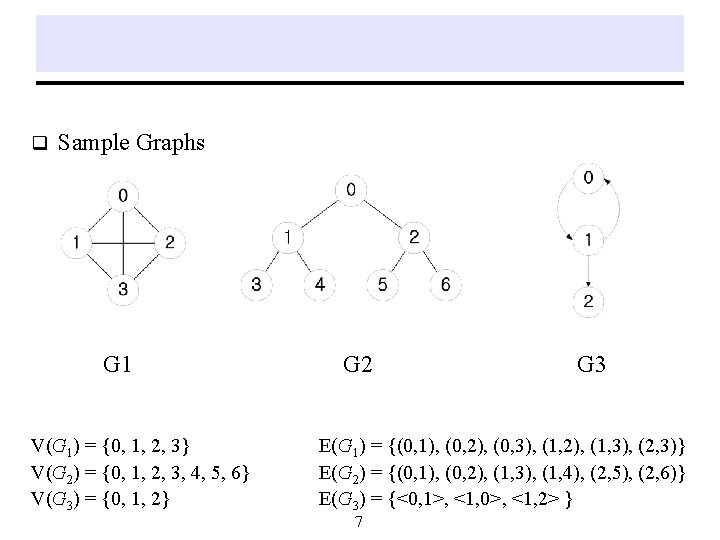
q Sample Graphs G 1 V(G 1) = {0, 1, 2, 3} V(G 2) = {0, 1, 2, 3, 4, 5, 6} V(G 3) = {0, 1, 2} G 2 G 3 E(G 1) = {(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)} E(G 2) = {(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6)} E(G 3) = {<0, 1>, <1, 0>, <1, 2> } 7

Definitions q complete graph - graph that has the maximum number of edges. q adjacent, incident - q subgraph - q if (v 0, v 1) is an edge in an undirected graph, then the vertices v 0 and v 1 are adjacent and the edge (v 0, v 1) is incident on vertices v 0 and v 1 a subgraph of G is a graph G’ such that V(G’ ) V(G) and E(G’) E(G) path - a path from vertex vp to vertex vq in a graph, G, is a sequence of vertices, vp, vi 1, vi 2, … , vin , vq such that (vp, vi 1), (vi 1, vi 2), … , (vin , vq) are edges in an undirected graph. 9

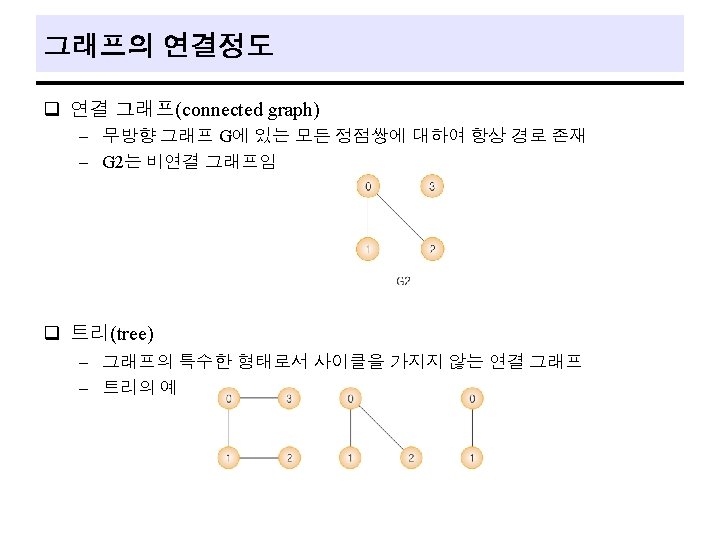
the length of a path is the number of edges on it. q simple path : path in which all vertices, except possibly the first and the last, are distinct. q cycle : simple path in which the first and the last vertices are the same. q connected q - In an undirected graph G, two vertices, v 0 and v 1, are connected if there is a path in G from v 0 to v 1. connected component : maximal connected subgraph q tree : graph that is connected and a cyclic (it has no cycles). q The degree of a vertex is the number of edges incident to the vertex. q 10

q restriction on graphs : 1. A graph may not have an edge from a vertex, i, back to itself. - self loops. 2. A graph may not have multiple occurrences of the same edge. - if we allow, multigraph. 15

Graph Representations q Adjacency Matrix - The adjacency matrix of G is a two-dimensional n n array, say adj_mat. - If the edge (vi, vj) ( <vi, vj> for a digraph) is in E(G), adj_mat[i][j] = 1. - If there is no edge in E(G), adj_mat[i][j] = 0. ex) 16

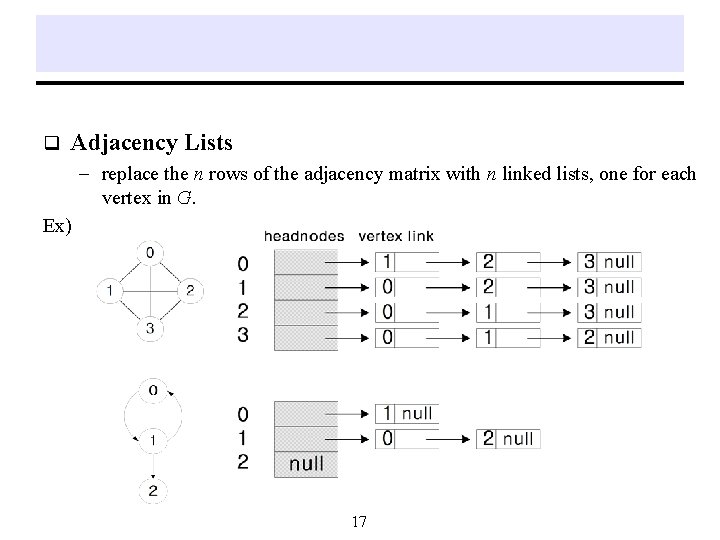
q Adjacency Lists - replace the n rows of the adjacency matrix with n linked lists, one for each vertex in G. Ex) 17

Depth First Search q Algorithm 1. begin the search by visiting the start vertex, v. 2. select an unvisited vertex, w, from v’s adjacency list and carry out a depth first search on w. (using recursion) 19

Depth First Search Function #define FALSE 0 #define TRUE 1 short int visited[MAX_VERTICES]; void dfs(int v) { /* depth first search of a graph beginning with vertex v. */ node_pointer w; visited[v]=TRUE; printf(“ 5 d”, v); for (w = graph[v]; w; w = w->link) if( !visited[w->vertex] ) dfs(w->vertex); } 20

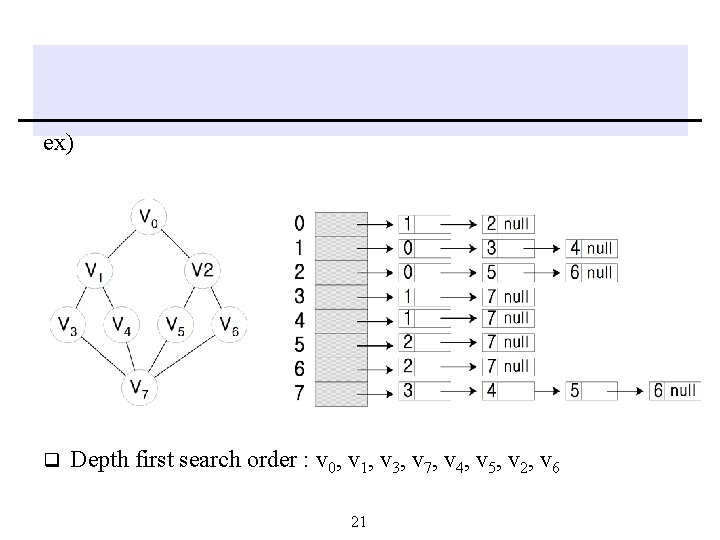
ex) q Depth first search order : v 0, v 1, v 3, v 7, v 4, v 5, v 2, v 6 21

Breadth First Search q Algorithm 1. starts at vertex v and marks it as visited. 2. visits each of the vertices on v’s adjacency list. 3. when we have visited all the vertices on v’s adjacency list, we visit all the unvisited vertices that are adjacent to the first vertex on v’s adjacency list. - using queue. 22

Connected Components q whether or not an undirected graph is connected? - q Calling either dfs(0) of bfs(0) and then determining if there any unvisited vertices. Listing the connected components of a graph. void connected(void) { /* determine the connected components of a graph */ int i; for ( i = 0; i < n; i++ ) if ( !visited[i] ) { dfs(i); printf(“n”); } } 23

Biconnected Components And Articulation Points q Definition An articulation point is a vertex v of G such that the deletion of v, together with all edges incident on v, produces a graph, G’ that has at least two connected components. - A biconnected graph is a connected graph that has no articulation points. - A biconnected component of a connected undirected graph is a maximal biconnected subgraph, H, of G. The maximal biconnected subgraph means that G contains no other subgraph that is both biconnected and properly contains H. - 24

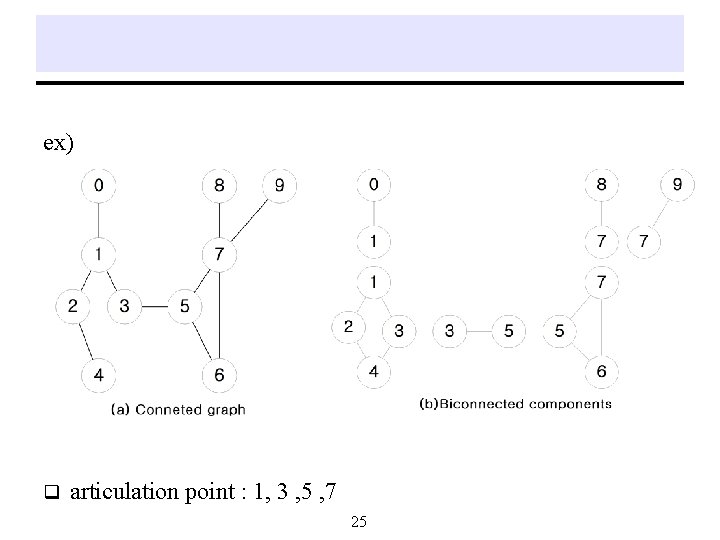
ex) q articulation point : 1, 3 , 5 , 7 25

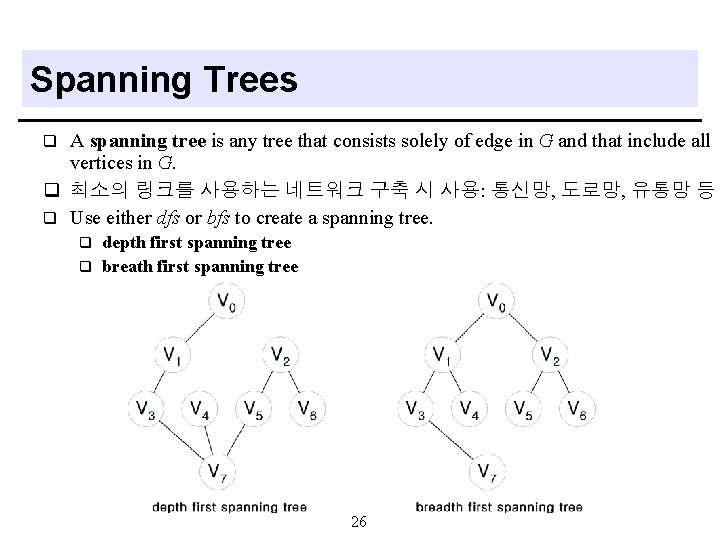
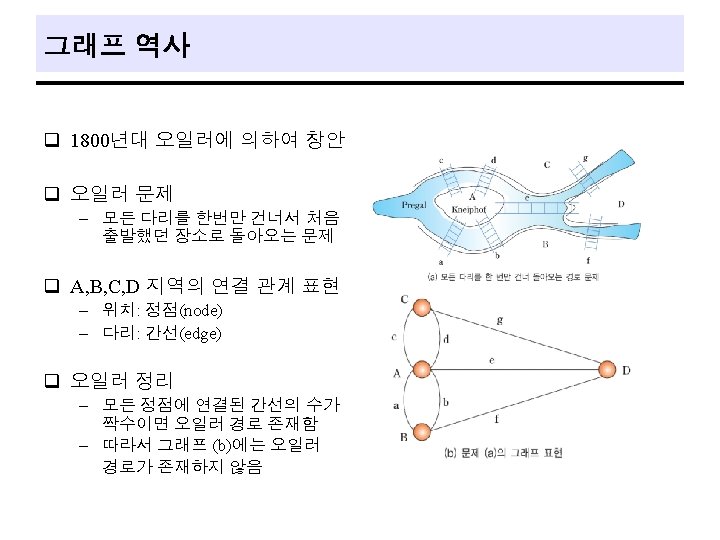
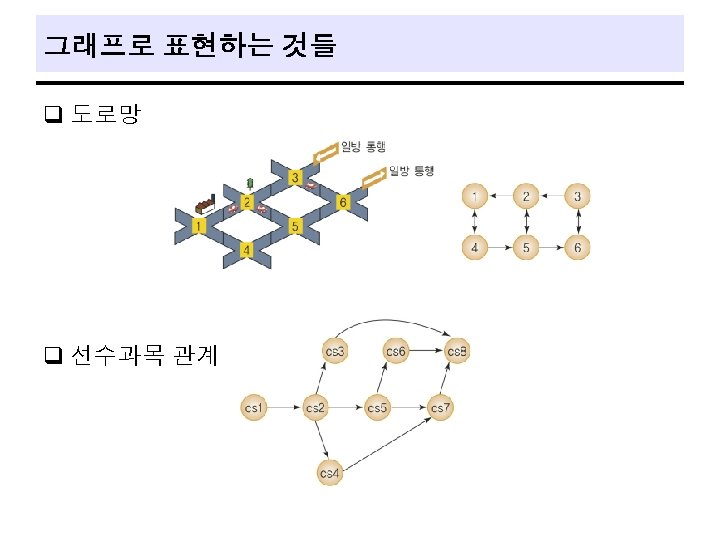
Spanning Trees A spanning tree is any tree that consists solely of edge in G and that include all vertices in G. q 최소의 링크를 사용하는 네트워크 구축 시 사용: 통신망, 도로망, 유통망 등 q Use either dfs or bfs to create a spanning tree. q depth first spanning tree q breath first spanning tree q 26

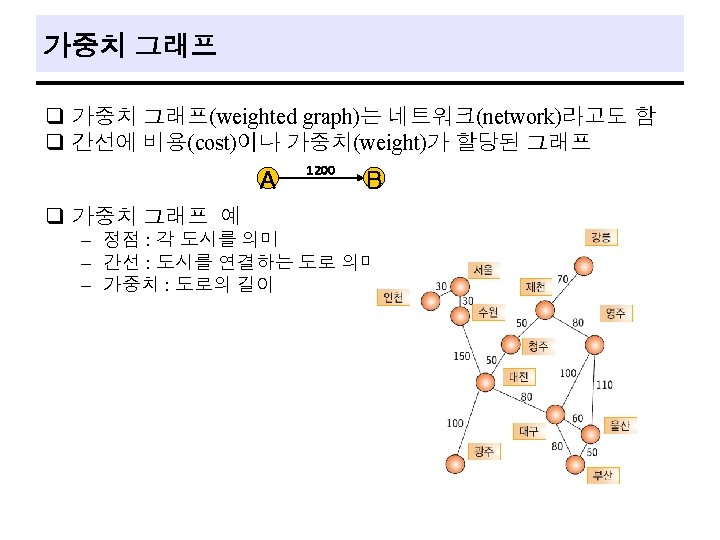
Minimum Cost Spanning Trees q Definition - cost of a spanning tree of a weighted undirected graph : the sum of the costs(weights) of the edges in the spanning tree - Minimum cost spanning tree : a spanning tree of least cost q 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결 q MST의 응용 – 도로 건설 - 도시들을 모두 연결하면서 도로의 길이를 최소가 되도록 하는 문 제 – 전기 회로 - 단자들을 모두 연결하면서 전선의 길이를 가장 최소로 하는 문제 – 통신 - 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제 – 배관 - 파이프를 모두 연결하면서 파이프의 총 길이를 최소로 하는 문제 q Three algorithms for minimum cost spanning tree - Kruskal’s, Prim’s, Sollin’s algorithms - All three use an greedy method 27

Minimum Cost Spanning Trees (Cont’d) q Greedy method - At each stage, make a decision that is the best decision (using the criterion). - Since we cannot change this decision later, we make sure that the decision will result in a feasible solution. - Typical criterion : least cost, highest profit criterion q Constraints for minimum cost spanning tree algorithms 1. Must use only edges within the graph. 2. Must use exactly n-1 edges. 3. May not use edges that would produce a cycle. 28

Kruskal’s Algorithm q Methods - build a minimum cost tree T by adding edges to T one at a time selects the edges for inclusion in T in nondecreasing order of their cost an edge is added in T if it does not form a cycle graph G is connected and has n>0 vertices, exactly n-1 edges will be selected 29

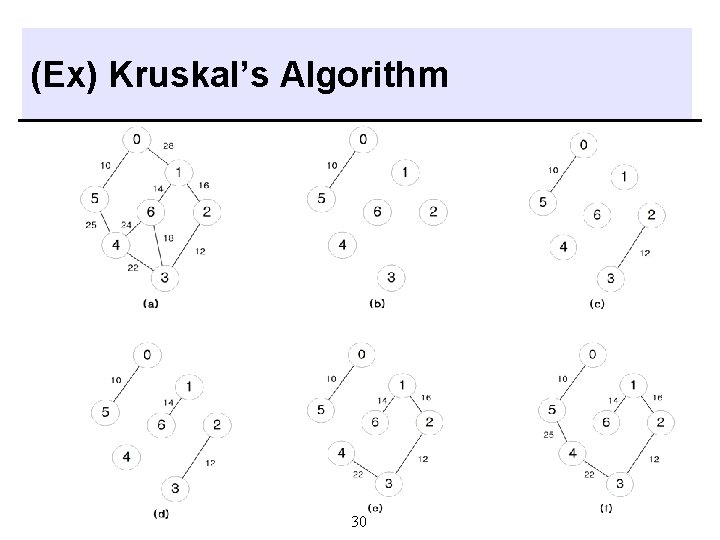
(Ex) Kruskal’s Algorithm 30

Prim’s Algorithm q Methods - constructs the minimum cost spanning tree one edge at a time. at each stage, the set of selected edges forms a tree. begins with a tree, T, that contains a single vertex. add a least cost edge (u, v) to T such that T {(u, v)} is also a tree. repeat until n-1 edges are selected. 31

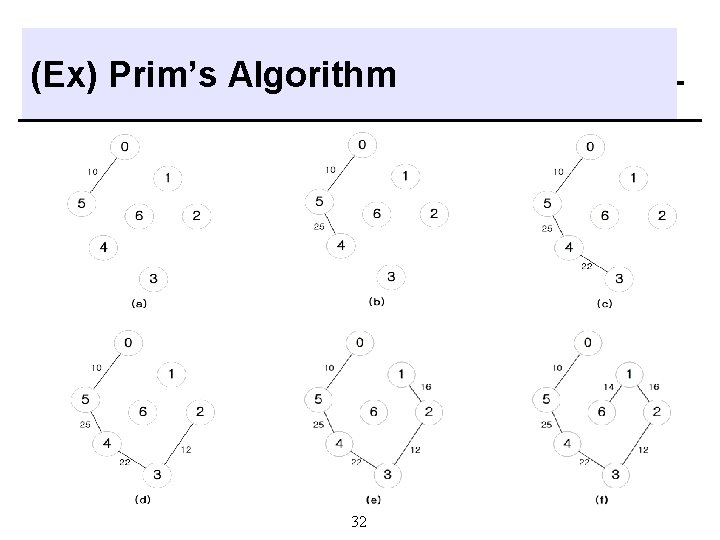
(Ex) Prim’s Algorithm 32

Sollin’s Algorithm q Methods - select several edges for inclusion in T at each stage. - at the start of the stage, the selected edges, together with all n graph vertices, form a spanning forest. - during a stage, select one edge for each tree in the forest. - Since two trees in the forest could select the same edge, need to eliminate multiple copies of edges. - at start of the first stage the set of selected edges is empty. - terminates when there is only tree at the end of a stage or no edges remain for selection. 33

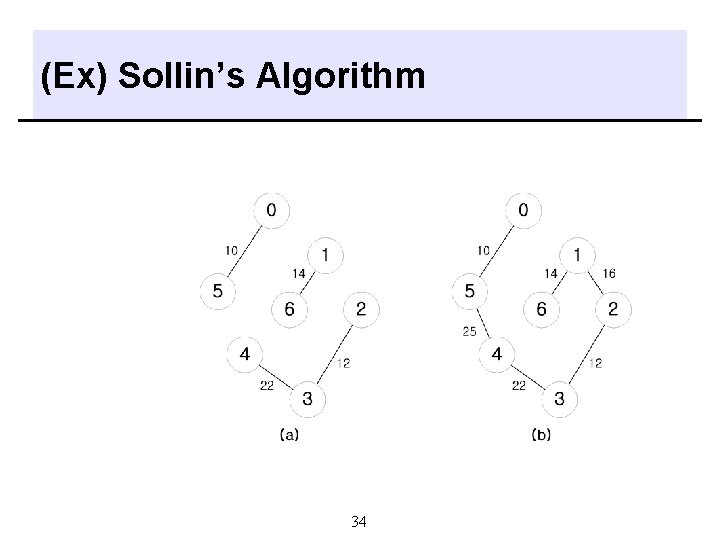
(Ex) Sollin’s Algorithm 34

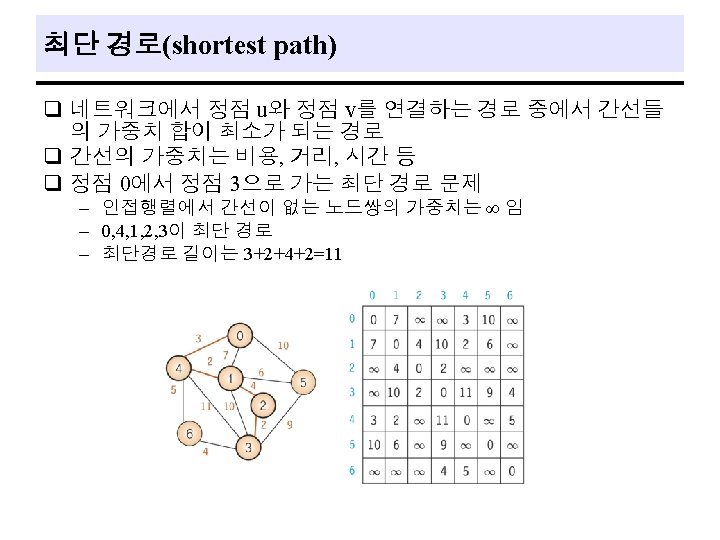
Shortest paths and Transitive closure q Problem 1. Is there a path from A to B? 2. If there is more than one path from A to B, which path is the shortest? q Assume - the length of a path as the sum of the weights of the edges on that path rather than the number of edges on the path - since one-way streets are possible, the graphs are directed. - assume that all weights are positive 35

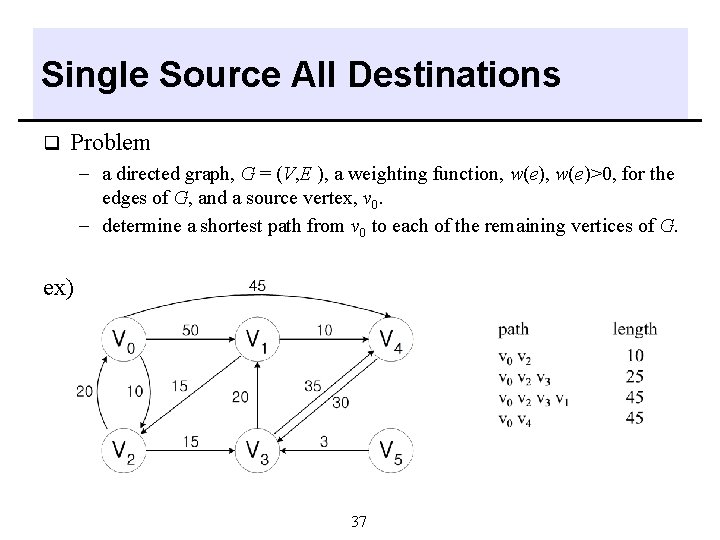
Single Source All Destinations q Problem - a directed graph, G = (V, E ), a weighting function, w(e)>0, for the edges of G, and a source vertex, v 0. - determine a shortest path from v 0 to each of the remaining vertices of G. ex) 37

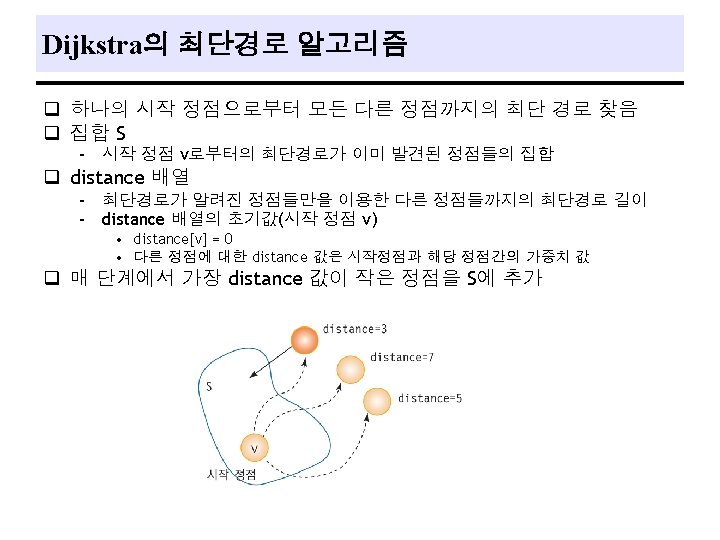
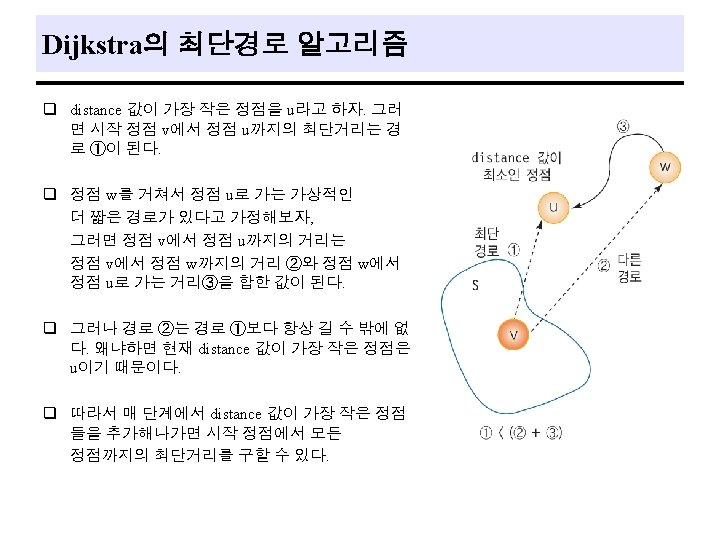
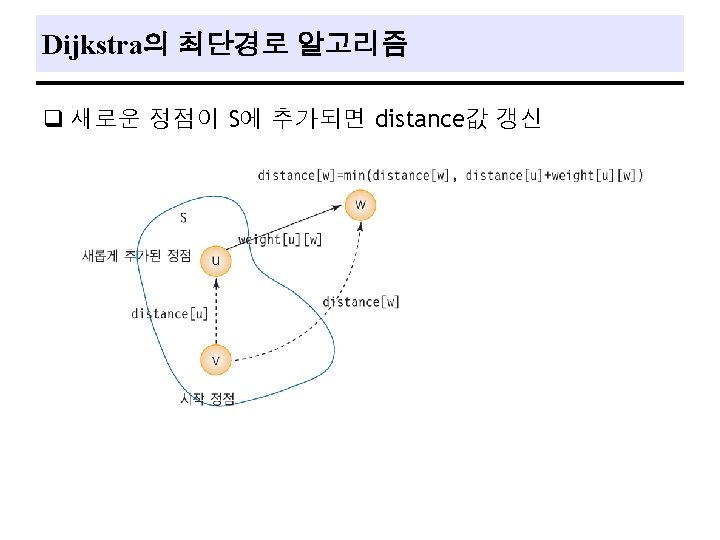
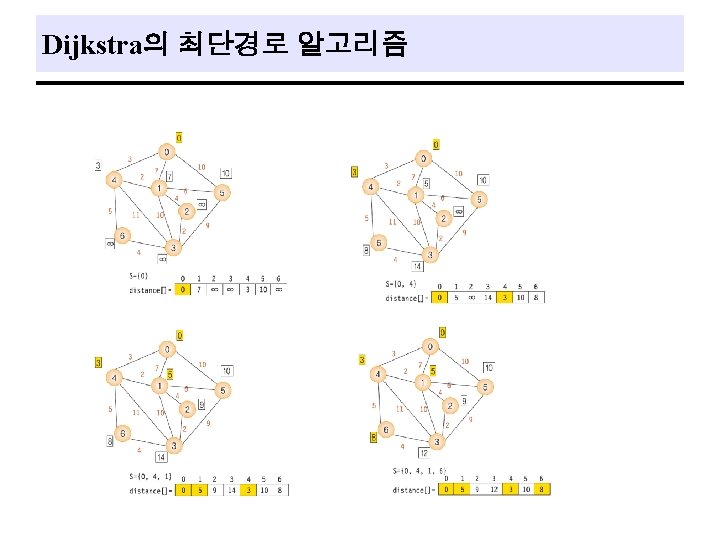
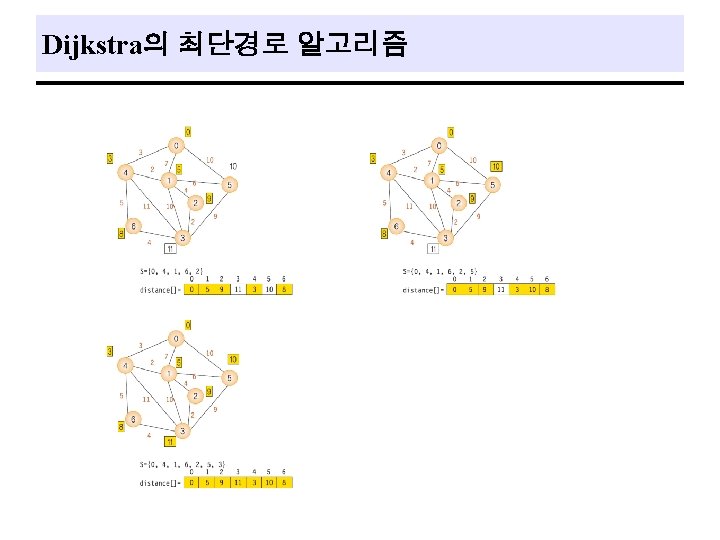
Dijkstra의 최단경로 프로그램 #include <stdio. h> #include <limits. h> #define TRUE 1 #define FALSE 0 #define MAX_VERTICES 7 // 정점의 수 #define INF 1000 // 무한대 (연결이 없는 경우) int weight[MAX_VERTICES]={ // 네트워크의 인접 행렬 { 0, 7, INF, 3, 10, INF }, { 7, 0, 4, 10, 2, 6, INF }, { INF, 4, 0, 2, INF, INF }, { INF, 10, 2, 0, 11, 9, 4 }, { 3, 2, INF, 11, 0, INF, 5 }, { 10, 6, INF, 9, INF, 0, INF }, { INF, 4, 5, INF, 0 }}; int distance[MAX_VERTICES]; // 시작정점으로부터의 최단경로 거리 int found[MAX_VERTICES]; // 방문한 정점 표시 // int choose(int distance[], int n, int found[]) { int i, minpos; min = INT_MAX; minpos = -1; for(i=0; i<n; i++) if( distance[i]< min && ! found[i] ){ min = distance[i]; minpos=i; } return minpos; }

Dijkstra의 최단경로 프로그램(cont. ) void shortest_path(int start, int n) { int i, u, w; for(i=0; i<n; i++) // 초기화 {distance[i] = weight[start][i]; found[i] = FALSE; } found[start] = TRUE; // 시작 정점 방문 표시 distance[start] = 0; for(i=0; i<n-2; i++){ u = choose(distance, n, found); found[u] = TRUE; for(w=0; w<n; w++) if(!found[w]) if( distance[u]+weight[u][w]<distance[w] ) distance[w] = distance[u]+weight[u][w]; } } // void main() { shortest_path(0, MAX_VERTICES); }

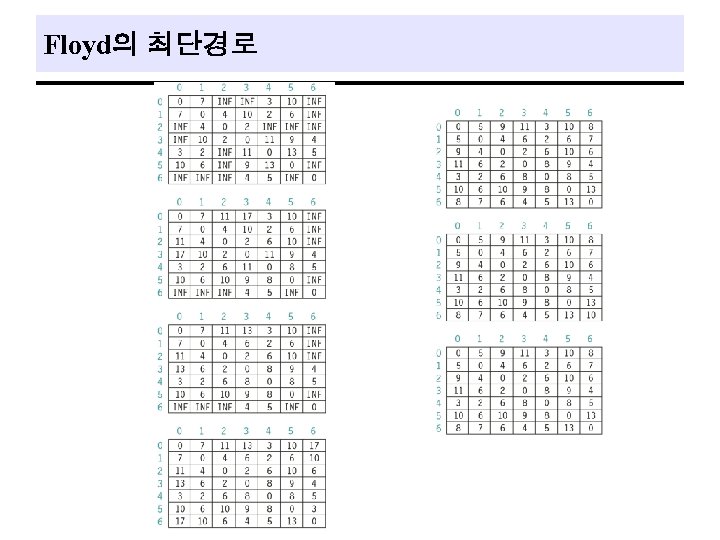
All Pairs Shortest Paths q Problem - find the shortest paths between all pairs of vertices, vi, vj, i j. q Solution 1. using shortestpath with each of the vertices in V(G) as the source : O(n 3). 2. Dynamic programming method : (n 3) with a smaller constant factor. 46

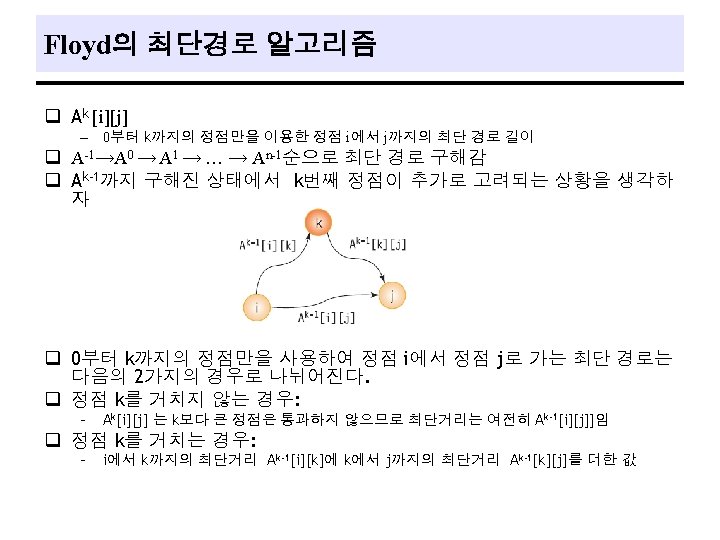
Floyd의 최단경로 프로그램 int A[MAX_VERTICES]; void floyd(int n) { int i, j, k; for(i=0; i<n; i++) for(j=0; j<n; j++) A[i][j]=weight[i][j]; for(k=0; k<n; k++) for(i=0; i<n; i++) for(j=0; j<n; j++) if (A[i][k]+A[k][j] < A[i][j]) A[i][j] = A[i][k]+A[k][j]; }

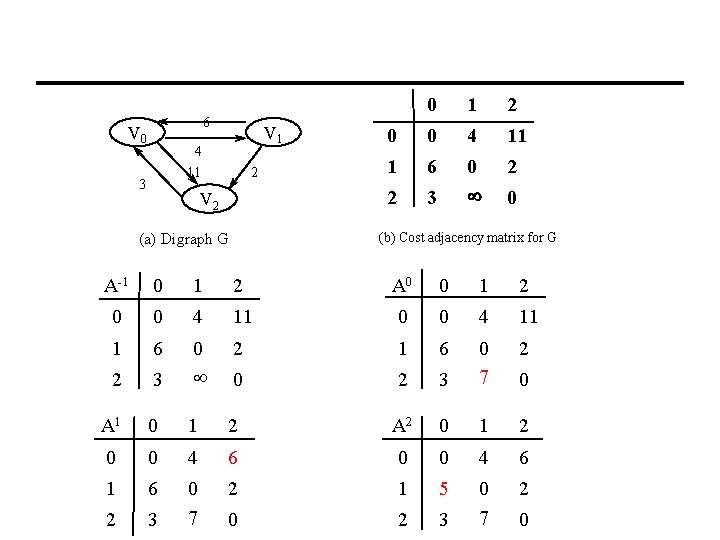
6 V 0 V 1 4 11 3 2 V 2 0 1 2 0 0 4 11 1 6 2 2 3 0 ¥ 0 (b) Cost adjacency matrix for G (a) Digraph G A-1 0 1 2 A 0 0 1 2 0 0 4 11 1 6 2 1 6 3 0 2 3 0 7 2 2 0 ¥ A 1 0 1 2 A 2 0 1 2 0 0 4 6 1 6 2 1 5 3 0 2 3 0 7 2 2 0 7 0 0