Data Structures for Java William H Ford William

Representing Graphs • Adjacency matrix representation of a graph uses a matrix whose entries

Representing Graphs (concluded) • An Adjacency list representation of a graph includes the vertex

Di. Graph Components • The Edge class holds data that references the destination of

Edge Class class Edge { // index of the destination vertex in the Array.

Representing Vertex Information • The Vertex. Info class has a reference to the vertex

Vertex. Info Class // maintains vertex properties, including // its set of Edges class

Vertex. Info Class (continued) // indicates vertex color for use in algorithms // that

Vertex. Info Class (concluded) // constructor creates an object with initial // values for

Vertex. Color Class The Vertex. Color class maintains the color of a vertex. The

The Vertex Map and Vertex. Info Array. List • The vertex map contains key‑value

The Vertex Map and Vertex. Info Array. List (concluded) © 2005 Pearson Education, Inc.

Exploring the Adjacency List of a Vertex • A Vertex. Info object allows access

Exploring the Adjacency List of a Vertex (continued) • Let us look at a

Exploring the Adjacency List of a Vertex (continued) // iterator to scan adjacency list

Exploring the Adjacency List of a Vertex (continued) // output the edge that has

The occupied Field • Occupied field of a Vertex. Info object indicates if the

Di. Graph Class Design • The class provides an availability stack to store indices

Di. Graph Class Design (continued) © 2005 Pearson Education, Inc. , Upper Saddle River,

Di. Graph Class Methods • The method get. VInfo. Index() takes a vertex as

get. VInfo. Index() • Private method get. VInfo. Index() looks up a vertex in

Getting Neighbors • The get. Neighbors() method scans the adjacency list of a vertex

get. Neighbors() // returns the vertices that are adjacent to // vertex v in

get. Neighbors() (concluded) // create Hash. Set object to hold vertices, // obtain the

Adding an Edge • To add an edge to a graph, obtain the v.

Adding an Edge (continued) pos 1=get. VInfo. Index(v 1); pos 2=get. VInfo. Index(v 2);

Erasing a Vertex • To erase a vertex remove all of the edges to

Erasing a Vertex (continued) • Task 1: Get the Vertex. Info object in v.

Erasing a Vertex (continued) • Task 2: Delete all edges that terminate in v.

Erasing a Vertex (continued) // remove all the edges that terminate at the vertex

Erasing a Vertex (continued) // check if vertex is valid if (edge. Vtx. Info.

Erasing a Vertex (continued) • Task 3: Delete all edges that emanate from v.

Erasing a Vertex (concluded) // reduce num. Edges by number of elements in adjacency

Efficiency of add. Edge() and remove. Vertex() Methods • The running time for adding

Graph Algorithm Support Methods • The Di. Graph class includes access and update methods

get. Color() // returns the color of vertex v; if v is not //

set. Parent() // assigns the parent of vertex v to be p and returns

set. Parent() (concluded) if (pos 1 != -1 && pos 2 != -1) {

color. White() // sets the color of each vertex to Vertex. Color. WHITE; //

Graph Collection View • The method vertex. Set() returns a set view of the

Set view remove() public boolean remove(Object item) { boolean ret. Value = false; if

Di. Graph Iterators • The implementation of the graph set view iterator uses an

Di. Graph Inner Class Iterator. Impl // implements graph iterators private class Iterator. Impl

Di. Graph Inner Class Iterator. Impl (continued) public T next() { last. Value =

Di. Graph Inner Class Iterator. Impl (concluded) // find the index of last. Value

Slides: 45

Download presentation

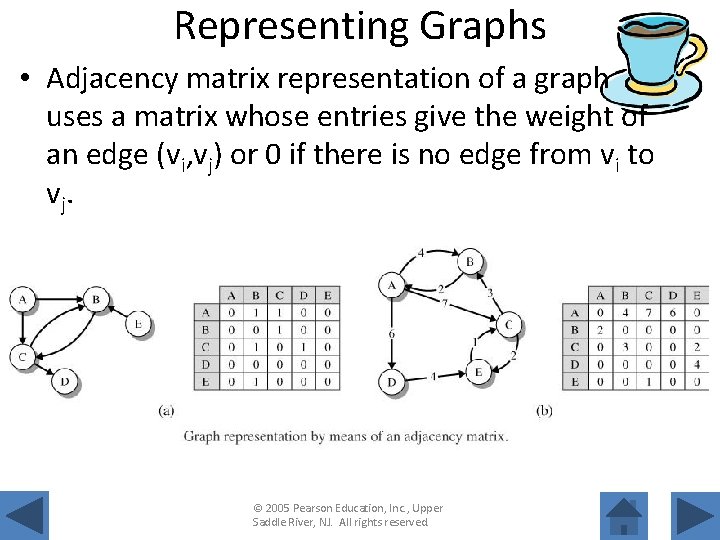
Representing Graphs • Adjacency matrix representation of a graph uses a matrix whose entries give the weight of an edge (vi, vj) or 0 if there is no edge from vi to v j. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

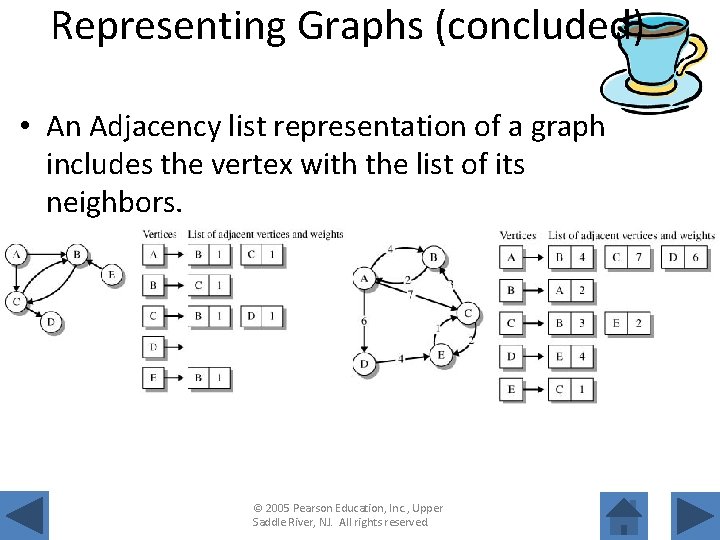
Representing Graphs (concluded) • An Adjacency list representation of a graph includes the vertex with the list of its neighbors. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Edge Class class Edge { // index of the destination vertex in the Array. List // v. Info of vertex properties public int dest; // weight of this edge public int weight; public Edge(int dest, int weight) { this. dest = dest; this. weight = weight; } public boolean equals(Object obj) { return ((Edge)obj). dest == this. dest; } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

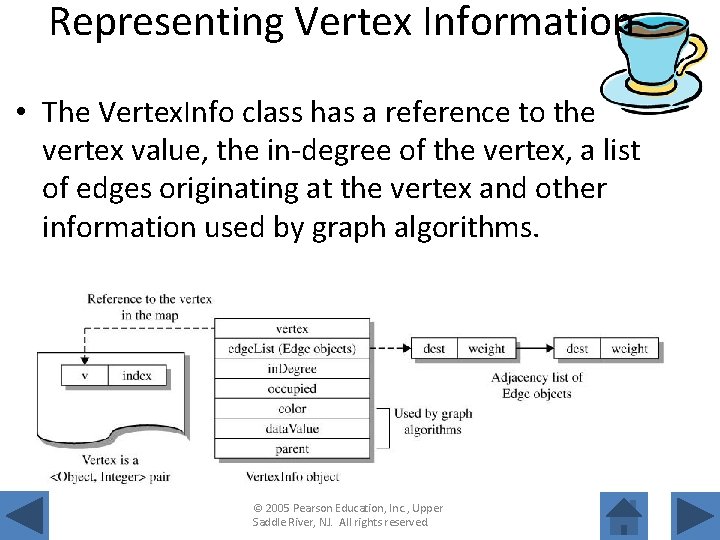
Representing Vertex Information • The Vertex. Info class has a reference to the vertex value, the in-degree of the vertex, a list of edges originating at the vertex and other information used by graph algorithms. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Vertex. Info Class // maintains vertex properties, including // its set of Edges class Vertex. Info<T> { // vertex reference back to the vertex in the map public T vertex; // list of Edge objects (adjacent vertices) for the // current vertex public Linked. List<Edge> edge. List; // maintains the in-degree of the vertex public int in. Degree; public int out. Degree; // indicates whether the object currently // represents a vertex public boolean occupied; © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Vertex. Info Class (continued) // indicates vertex color for use in algorithms // that traverse the vertices of a Graph public Vertex. Color color; // available to algorithms for storing relevant // data values public int data. Value; // available to Graph algorithms; holds parent // which is a vertex that has an edge terminating // in the current vertex public T parent; © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Vertex. Info Class (concluded) // constructor creates an object with initial // values for the vertex, edge. List, in. Degree, // and occupied fields public Vertex. Info(T v) { vertex = v; edge. List = new Linked. List<Edge>(); in. Degree = 0; occupied = true; } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Vertex. Color Class The Vertex. Color class maintains the color of a vertex. The colors of WHITE, GRAY, and BLACK are values of the enumerated type. public enum Vertex. Color { WHITE, GRAY, BLACK } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

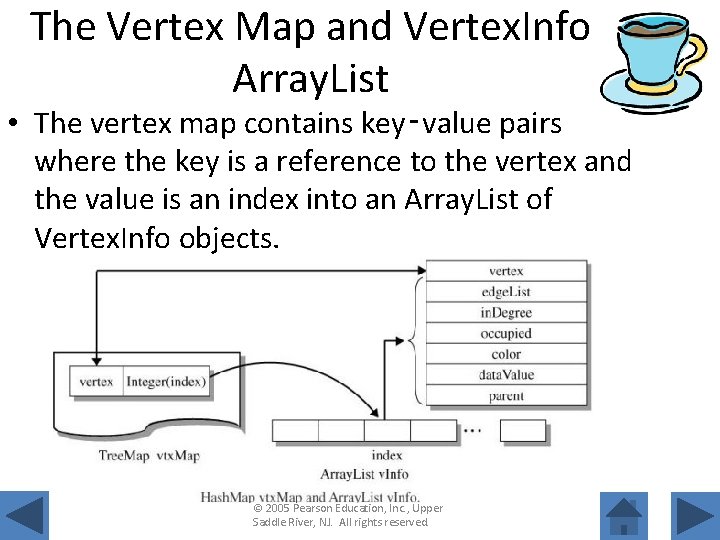
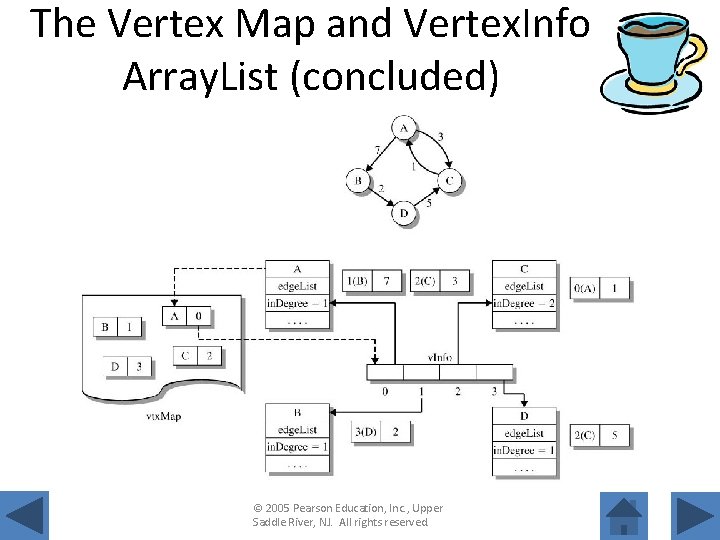
The Vertex Map and Vertex. Info Array. List • The vertex map contains key‑value pairs where the key is a reference to the vertex and the value is an index into an Array. List of Vertex. Info objects. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Exploring the Adjacency List of a Vertex • A Vertex. Info object allows access to all the neighbors of the vertex. Vertex. Info<T> vtx. Info = v. Info. get(i); // declare an iterator for edge. List and position it at the first // element in the adjacency list Iterator<Edge> iter = vtx. Info. edge. List. iterator(); // extract the first element and output its weight Edge e = iter. next(); System. out. println(e. weight); // use the dest field to access the v. Info element that corresponds // to the adjacent vertex; the index of the element is e. dest; // output the name of the vertex Vertex. Info<T> edge. Vtx. Info = v. Info. get(e. dest); System. out. println(edge. Vtx. Info. vertex); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Exploring the Adjacency List of a Vertex (continued) • Let us look at a code segment that scans the adjacency list looking for the edge of minimum weight. In order to output the edge, we must maintain the v. Info index of the destination vertex. // declare variables for the minimum dest index and // minimum weight int min. Dest, min. Weight = Integer. MAX_VALUE; // Vertex. Info objects for elements in Array. List v. Info; // current vertex element in v. Info is vtx. Info; v. Info element // for a neighbor is edge. Vtx. Info Vertex. Info<T> vtx. Info = null, edge. Vtx. Info = null; . . . © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Exploring the Adjacency List of a Vertex (continued) // iterator to scan adjacency list for current vertex Iterator<Edge> iter = vtx. Info. edge. List. iterator(); while (iter. has. Next) { // extract next element (Edge object) from adjacency list Edge e = iter. next(); // update if new minimum weight is discovered if (e. weight < min. Weight) { min. Weight = e. weight; min. Dest = e. dest; } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Exploring the Adjacency List of a Vertex (continued) // output the edge that has minimum weight; first get the // corresponding v. Info element and then access the vertex field edge. Vtx. Info = v. Info. get(min. Dest); System. out. println("Edge (" + vtx. Info. vertex + ", " + edge. Vtx. Info. vertex + ") has weight + edge. Vtx. Info. weight); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

The occupied Field • Occupied field of a Vertex. Info object indicates if the object corresponds to an existing vertex entry in the map. for (i = 0; i < v. Info. size(); i++) { Vertex. Info<T> vtx. Info = v. Info. get(i); if (vtx. Info. occupied) < v. Info element corresponds to an actual vertex> } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Class Design • The class provides an availability stack to store indices for the Array. List. Whenever a vertex is deleted from the map, push the index for the corresponding v. Info element onto the stack. When adding a new vertex, check to see whether an index is available on the stack. If so, pop it and reuse the corresponding v. Info element to store vertex properties, thus insuring more efficient memory management. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Class Methods • The method get. VInfo. Index() takes a vertex as an argument and returns the index of the corresponding element in the Array. List. The index is in the value field of the vtx. Map entry. A return value -1 indicates that the vertex is not in the graph. This method is used by many Di. Graph class methods. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

get. VInfo. Index() • Private method get. VInfo. Index() looks up a vertex in the map and returns the v. Info index of the vertex. // takes vertex v in the map and returns the // index of the corresponding v. Info element // or -1 if v is not a vertex private int get. VInfo. Index(Object v) { // get the Integer value field of the vtx. Map entry Integer index. Obj = vtx. Map. get(v); // // // if if value is null, there is not entry in the map; return -1; otherwise, convert object to an int (index. Obj == null) return -1; else return index. Obj; } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Getting Neighbors • The get. Neighbors() method scans the adjacency list of a vertex and returns a set containing its neighbors. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

get. Neighbors() // returns the vertices that are adjacent to // vertex v in a Set object; if v is not a graph // vertex, throws Illegal. Argument. Exception public Set<T> get. Neighbors(T v) { // find the Vertex. Info object for index v int index = get. VInfo. Index(v); // check for an error and throw exception // if vertices not in graph if (index == -1) throw new Illegal. Argument. Exception( "Di. Graph get. Neighbors(): vertex not in graph"); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

get. Neighbors() (concluded) // create Hash. Set object to hold vertices, // obtain the Vertex. Info object, and initialize // an iterator to scan the adjacency list of // the Vertex. Info object Hash. Set<T> edge. Set = new Hash. Set<T>(); Vertex. Info<T> vtx. Info = v. Info. get(index); Iterator<Edge> iter = vtx. Info. edge. List. iterator(); Edge e = null; while (iter. has. Next()) { e = iter. next(); edge. Set. add(v. Info. get(e. dest). vertex); } return edge. Set; } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Adding an Edge • To add an edge to a graph, obtain the v. Info index of the source vertex and insert an Edge object for the destination vertex in the adjacency list. Update the in-degree of the destination vertex. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Adding an Edge (continued) pos 1=get. VInfo. Index(v 1); pos 2=get. VInfo. Index(v 2); // get Vertex. Info objects for vertices v 1 and v 2 Vertex. Info<T> vtx. Info 1 = v. Info. get(pos 1), vtx. Info 2 = v. Info. get(pos 2); Edge e = new Edge(pos 2, w); boolean return. Value = true; // try to add an Edge reference v 1 -v 2. // if it already exists, just return if (!vtx. Info 1. edge. List. contains(e)) { vtx. Info 1. edge. List. add(e); // increment in. Degree for vertex v 2 and number of edges vtx. Info 2. in. Degree++; num. Edges++; } else return. Value = false; return. Value; © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (continued) • Task 1: Get the Vertex. Info object in v. Info that corresponds to the index. Set the occupied field to false and then push the index onto an availability stack for use by a vertex that might be added later. // iterator used to scan Edge objects in adjacency lists Iterator<Edge> iter = null; Edge e = null; Vertex. Info<T> vtx. Info = v. Info. get(index), edge. Vtx. Info; vtx. Info. occupied = false; avail. Stack. push(index); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (continued) • Task 2: Delete all edges that terminate in v. These edges have the form (vi, v) and are found by scanning all of the elements in v. Info. Extract the adjacency list for each vertex and use an iterator to scan the element, removing the Edge object that indicates v is an adjacent vertex. Decrement of the variable num. Edges with each edge deletion. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (continued) // remove all the edges that terminate at the vertex being // removed. use a loop to check all of the Vertex. Info // elements in v. Info for which occupied is true; these // correspond to actual vertices in the map for (int i = 0; i < v. Info. size(); i++) { // get the Vertex. Info object for index i edge. Vtx. Info = v. Info. get(i); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (continued) // check if vertex is valid if (edge. Vtx. Info. occupied) { // obtain an iterator to scan the adjacency list iter = edge. Vtx. Info. edge. List. iterator(); while (iter. has. Next()) { // get the Edge object and check if the dest field // has value index which identifies vertex v; if so // remove it and decrement num. Edges e = iter. next(); if (e. dest == index) { iter. remove(); num. Edges--; break; } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (continued) • Task 3: Delete all edges that emanate from v. These edges constitute the adjacency list for the vertex. First, determine the number of edges and decrement num. Edges. Then, search the list of Edge objects and decrement the indegree for each adjacent vertex. Delete each edge during the scan. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Erasing a Vertex (concluded) // reduce num. Edges by number of elements in adjacency list num. Edges -= vtx. Info. edge. List. size(); // scan the adjacency list for vertex v and decrement the // in-degree for each adjacent vertex iter = vtx. Info. edge. List. iterator(); while (iter. has. Next()) { e = iter. next(); edge. Vtx. Info = v. Info. get(e. dest); iter. remove(); edge. Vtx. Info. in. Degree--; } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Efficiency of add. Edge() and remove. Vertex() Methods • The running time for adding a vertex is O(E) and for removing a vertex is O(V + E). © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Graph Algorithm Support Methods • The Di. Graph class includes access and update methods for the color, data, and parent reference properties of a vertex. The properties are found in the Vertex. Info object corresponding to the vertex. The implementations are relatively simple. Identify the object and access the appropriate field. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

get. Color() // returns the color of vertex v; if v is not // a graph vertex, throws Illegal. Argument. Exception; // for use by graph algorithms public Vertex. Color get. Color(T v) { // find the v. Info index for v int pos = get. VInfo. Index(v); if (pos != -1) return v. Info. get(pos). color; else // throw an exception throw new Illegal. Argument. Exception( "Di. Graph get. Color(): vertex not in graph"); } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

set. Parent() // assigns the parent of vertex v to be p and returns // the previous parent; if v or p is not a graph // vertex, throws Illegal. Argument. Exception; for use // by graph algorithms public T set. Parent(T v, T p) { // find the v. Info index for v int pos 1 = get. VInfo. Index(v), pos 2 = get. VInfo. Index(p); Vertex. Info<T> vtx. Info; T old. Parent = null; © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

set. Parent() (concluded) if (pos 1 != -1 && pos 2 != -1) { vtx. Info = v. Info. get(pos 1); old. Parent = vtx. Info. parent; vtx. Info. parent = p; } else // throw an exception throw new Illegal. Argument. Exception( "Di. Graph set. Parent(): vertex not in graph"); return old. Parent; } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

color. White() // sets the color of each vertex to Vertex. Color. WHITE; // for use by graph algorithms public void color. White() { Vertex. Info<T> vtx. Info; for (int i = 0; i < v. Info. size(); i++) { vtx. Info = v. Info. get(i); if (vtx. Info. occupied) vtx. Info. color = Vertex. Color. WHITE; } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Graph Collection View • The method vertex. Set() returns a set view of the graph vertices. The implementation of vertex. Set() is similar to the implementation for a set view of map keys or entries. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Set view remove() public boolean remove(Object item) { boolean ret. Value = false; if (vtx. Map. contains. Key(item)) { remove. Vertex(item); ret. Value = true; } return ret. Value; } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Iterators • The implementation of the graph set view iterator uses an inner class Iterator. Impl similar to iterator implementations we have discussed for the Linked. List and other collections. The class includes a variable that is an iterator for the key. Set collection view associated with the vertex map. © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Inner Class Iterator. Impl // implements graph iterators private class Iterator. Impl implements Iterator<T> { Iterator<T> iter; T last. Value = null; public Iterator. Impl() { // iter traverses the map vertices iter = vtx. Map. key. Set(). iterator(); } public boolean has. Next() { return iter. has. Next(); } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Inner Class Iterator. Impl (continued) public T next() { last. Value = iter. next(); return last. Value; } public void remove() { if (last. Value == null) throw new Illegal. State. Exception( "Graph vertex set iterator call " + "to next() required before calling " + "remove()"); © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.

Di. Graph Inner Class Iterator. Impl (concluded) // find the index of last. Value in v. Info int index = get. VInfo. Index(last. Value); // remove the current vertex from the map iter. remove(); // remove all edges that terminate at // last. Value, and update the in-degree // of each neighbor of last. Value remove. Fixup(index); } } © 2005 Pearson Education, Inc. , Upper Saddle River, NJ. All rights reserved.