Data Structures CS 212 D Week 2 Arrays

Data Structures (CS 212 D) Week # 2: Arrays

Data Structures q Data structure § A particular way of storing and organising data in a computer so that it can be used efficiently q Types of data structures § Based on memory allocation o Static (or fixed sized) data structures (Arrays) o Dynamic data structures (Linked lists) § Based on representation o Linear o Non-linear (Arrays/linked lists) (Trees/graphs)

Array: motivation q You want to store 5 numbers in a computer § Define 5 variables, e. g. num 1, num 2, . . . , num 5 q What, if you want to store 1000 numbers? § Defining 1000 variables is a pity! § Requires much programming effort q Any better solution? § Yes, some structured data type o Array is one of the most common structured data types o Saves a lot of programming effort (cf. 1000 variable names)

What is an Array? q A collection of data elements in which § all elements are of the same data type, hence homogeneous data o An array of students’ marks o An array of students’ names o An array of objects (OOP perspective!) § elements (or their references) are stored at contiguous/ consecutive memory locations q Array is a static data structure § An array cannot grow or shrink during program execution – its size is fixed

Basic concepts q Array name (data) q Index/subscript (0. . . 9) q The slots are numbered sequentially starting at zero (Java, C++) q If there are N slots in an array, the index will be 0 through N-1 § Array length = N = 10 § Array size = N x Size of an element = 40 q Direct access to an element

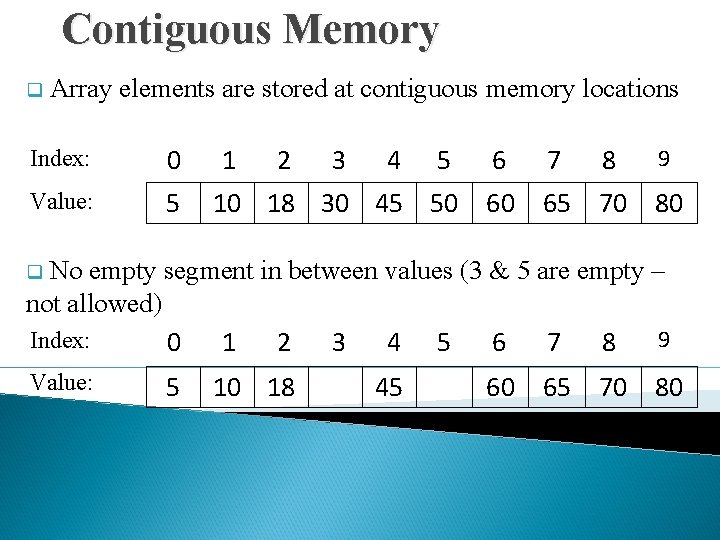
Homogeneity q All elements in the array must have the same data type Index: 0 Value: 5 1 2 3 5 4 6 7 8 9 10 18 30 45 50 60 65 70 80 Index: 0 1 Value: 5. 5 10. 2 Index: 0 1 Value: ‘A’ 10. 2 2 4 3 45. 6 18. 5 2 4 3 55 60. 5 ‘X’ 60. 5 Not an array

Contiguous Memory q Array elements are stored at contiguous memory locations Index: 0 Value: 5 1 2 3 4 5 6 7 8 9 10 18 30 45 50 60 65 70 80 q No empty segment in between values (3 & 5 are empty – not allowed) Index: 0 Value: 5 1 2 10 18 3 4 45 5 6 7 8 9 60 65 70 80

Declaring and Creating Arrays Declaring and Creating arrays ◦ Arrays are objects that occupy memory ◦ Created dynamically with keyword new int c[] = new int[ 12 ]; Equivalent to int c[]; // declare array variable c = new int[ 12 ]; // create array We can create arrays of objects too String b[] = new String[ 100 ];

Using Arrays q Array_name[index] q For example, in Java § System. out. println(data[4]) will display 0 § data[3] = 99 will replace -3 with 99

Using Arrays q Array_name[index] q For example, in Java § System. out. println(data[4]) will display 0 § data[3] = 99 will replace -3 with 99

Using Arrays Using an array initializer ◦ Use initializer list Items enclosed in braces ({}) Items in list separated by commas int n[] = { 10, 20, 30, 40, 50 }; Creates a five-element array Index values of 0, 1, 2, 3, 4 ◦ Do not need keyword new

Using Arrays (Cont. ) q To declare an array follow the type with (empty) []s int[] grade; //or int grade[]; //both declare an int array q In Java arrays are objects so must be created with the new keyword § To create an array of ten integers: int[] grade = new int[10]; Note that the array size has to be specified, although it can be specified with a variable at run-time

Examples Using Arrays (Cont. ) • Calculating the value to store in each array element – Initialize elements of 10 -element array to even integers

Examples Using Arrays (Cont. ) Init. Array. java Line 10 Declare array as an array of ints Line 12 Create 10 ints for array Line 16 Use array index to assign array value

Examples Using Arrays (Cont. )

Examples Using Arrays (Cont. ) Summing the elements of an array ◦ Array elements can represent a series of values We can sum these values

Examples Using Arrays (Cont. ) Histogram. java Line 9 Declare array with initializer list Line 19 For each array element, print associated number of asterisks

Examples Using Arrays (Cont. )

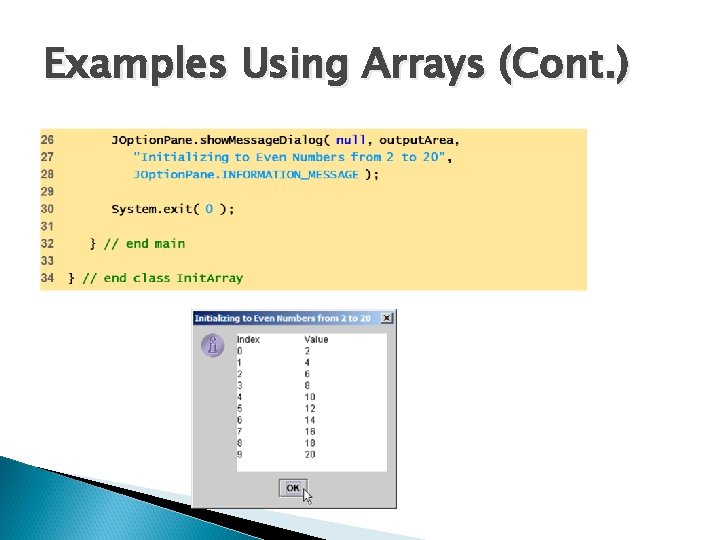
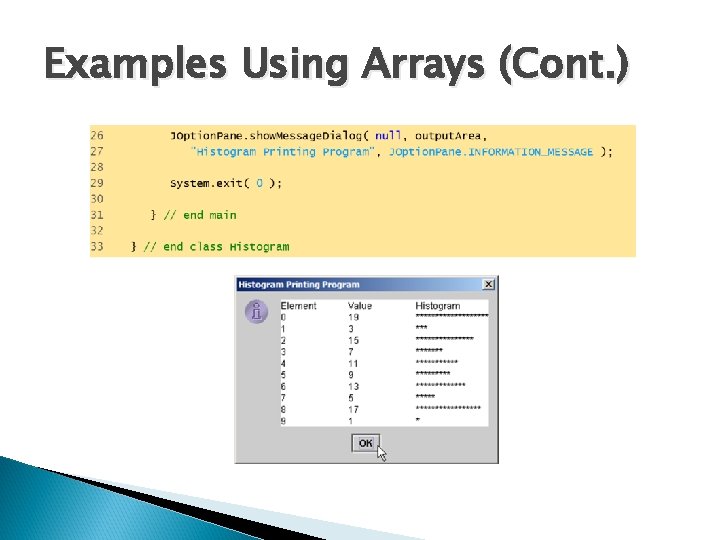
Some more concepts 1. 2. data[ -1 ] always illegal data[ 10 ] illegal (10 > upper bound) data[ 1. 5 ] always illegal data[ 0 ] always OK data[ 9 ] OK Q. What will be the output of? data[5] + 10 data[3] = data[3] + 10

Array’s Dimensionality q One dimensional (just a linear list) § e. g. , 5 10 18 30 45 50 60 65 70 80 § Only one subscript is required to access an individual element q Two dimensional (matrix/table) § e. g. , 2 x 4 matrix (2 rows, 4 columns) Row 0 Row 1 Col 0 20 30 Col 1 25 15 Col 2 60 70 Col 3 40 90

Multidimensional arrays ◦ Tables with rows and columns Two-dimensional array Declaring two-dimensional array b[2][2] int b[][] = { { 1, 2 }, { 3, 4 } }; 1 and 2 initialize b[0][0] and b[0][1] 3 and 4 initialize b[1][0] and b[1][1] int b[][] = { { 1, 2 }, { 3, 4, 5 } }; row 0 contains elements 1 and 2 row 1 contains elements 3, 4 and 5

Multidimensional arrays (Cont. ) Creating multidimensional arrays ◦ Can be allocated dynamically 3 -by-4 array int b[][]; b = new int[ 3 ][ 4 ]; Rows can have different number int b[][]; b = new int[ 2 ][ ]; // b[ 0 ] = new int[ 5 ]; // b[ 1 ] = new int[ 3 ]; // of columns allocate row 0 allocate row 1

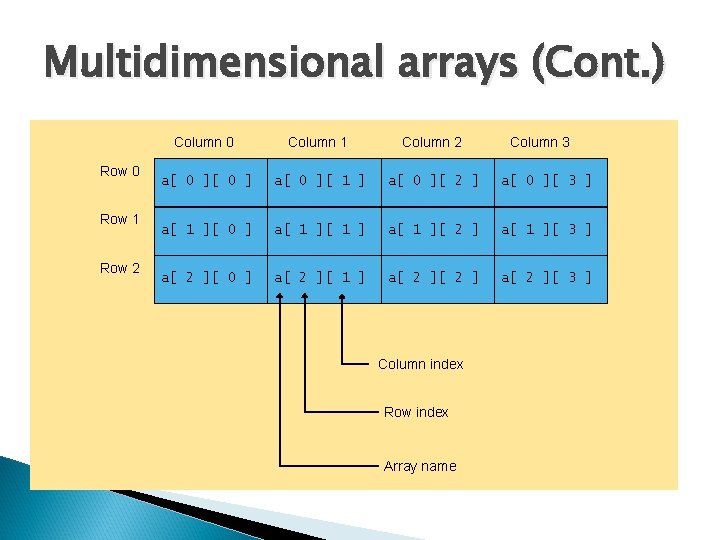
Multidimensional arrays (Cont. ) Row 0 Row 1 Row 2 Column 0 Column 1 Column 2 a[ 0 ][ 1 ] a[ 0 ][ 2 ] a[ 0 ][ 3 ] a[ 1 ][ 0 ] a[ 1 ][ 2 ] a[ 1 ][ 3 ] a[ 2 ][ 0 ] a[ 2 ][ 1 ] a[ 2 ][ 3 ] Column index Row index Array name Column 3

Multidimensional arrays (Cont. ) Init. Array. jav a Line 16 Declare array 1 with six initializers in two sublists Line 17 Declare array 2 with six initializers in three sublists

Multidimensional arrays (Cont. ) Init. Array. java Line 34 array[row]. leng th returns number of columns associated with row subscript Line 35 Use double-bracket notation to access twodimensional array values

Searching Arrays: Linear Search and Binary Searching ◦ Finding elements in large amounts of data Determine whether array contains value matching key value ◦ Linear searching ◦ Binary searching

Searching Arrays: Linear Search and Binary Search (Cont. ) Linear search ◦ Compare each array element with search key If search key found, return element index If search key not found, return – 1 (invalid index) ◦ Works best for small or unsorted arrays ◦ Inefficient for larger arrays

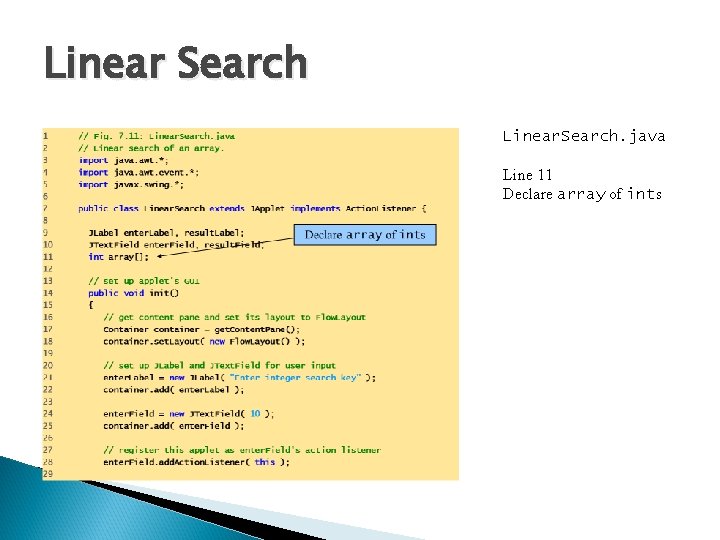
Linear Search Linear. Search. java Line 11 Declare array of ints

Linear Search(Cont. ) Linear. Search. java Lines 39 -42 Allocate 100 ints for array and populate array with even ints Line 50 Loop through array Lines 53 -54 If array element at index matches search key, return index

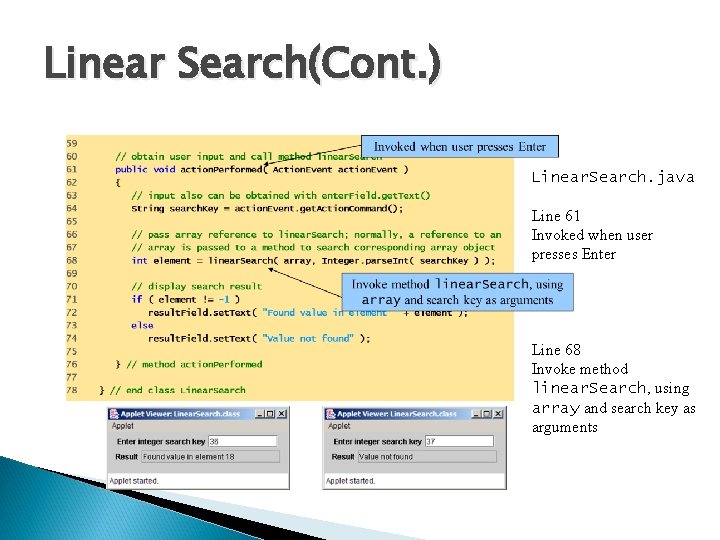
Linear Search(Cont. ) Linear. Search. java Line 61 Invoked when user presses Enter Line 68 Invoke method linear. Search, using array and search key as arguments

Binary Search Binary search ◦ Efficient for large, sorted arrays ◦ Eliminates half of the elements in search through each pass Compare middle array element to search key If element equals key Return array index If element is less than key Repeat search on first half of array If element is greater then key Repeat search on second half of array Continue search until element equals search key (success) Search contains one element not equal to key (failure)

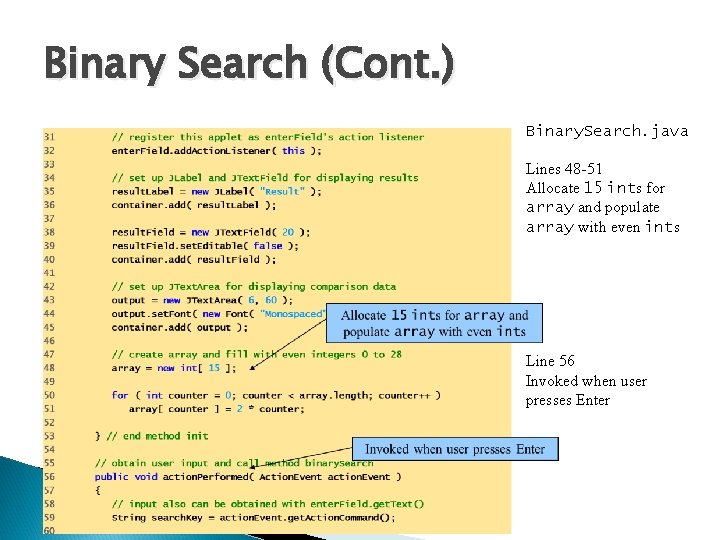
Binary Search (Cont. ) Binary. Search. java Line 14 Declare array of ints Declae array of ints

Binary Search (Cont. ) Binary. Search. java Lines 48 -51 Allocate 15 ints for array and populate array with even ints Line 56 Invoked when user presses Enter

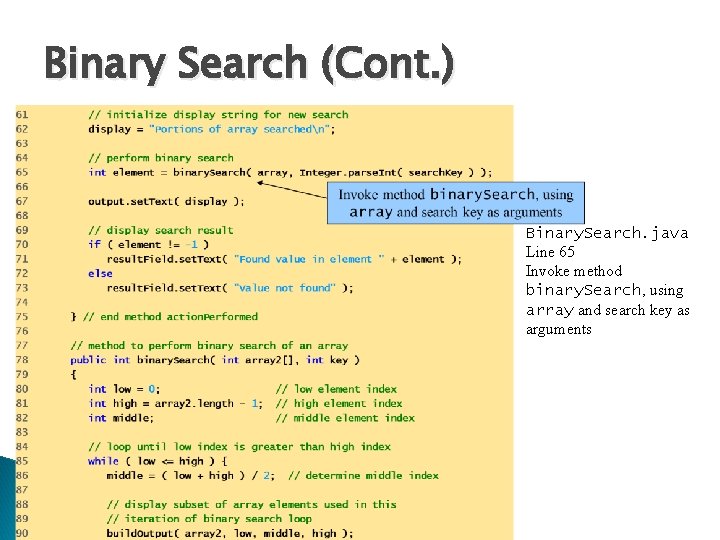
Binary Search (Cont. ) Binary. Search. java Line 65 Invoke method binary. Search, using array and search key as arguments

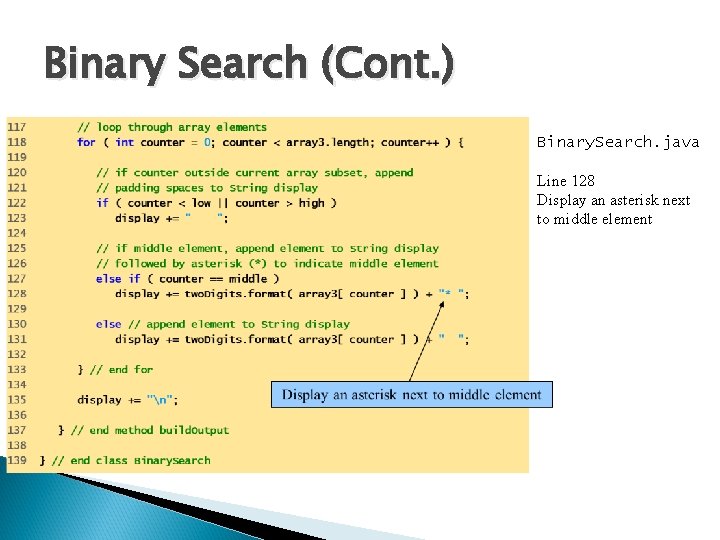
Binary Search (Cont. ) Binary. Search. java Lines 93 -94 If search key matches middle array element, return element index Lines 97 -98 If search key is less than middle array element, repeat search on first array half Lines 101 -102 If search key is greater than middle array element, repeat search on second array half Lines 112 -137 Method build. Output displays array contents being searched

Binary Search (Cont. ) Binary. Search. java Line 128 Display an asterisk next to middle element

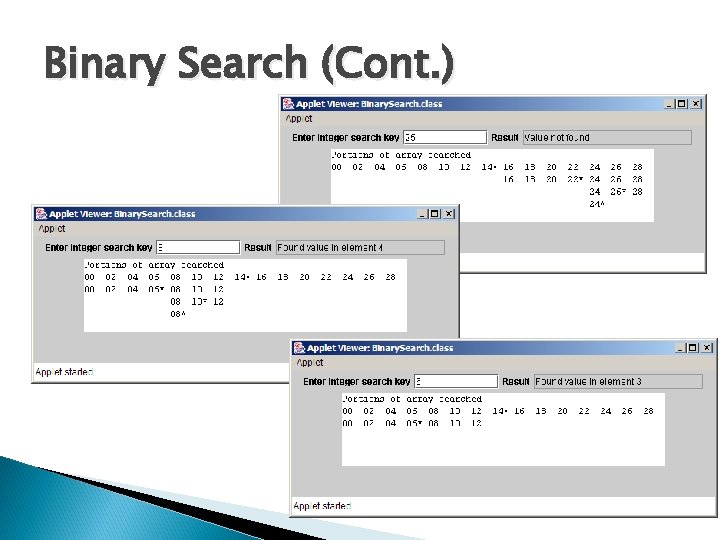
Binary Search (Cont. )

Sorting q Motivation q Generally, to arrange a list of elements in some order q List of numbers § 10 20 50 30 40 60 25 (Unsorted list) § 10 20 25 30 40 50 60 (Sorted list, ascending) § 60 50 40 30 25 20 10 (Sorted list, descending) q List of alphabets § P A K I S T A N § A A I K N P S T § T S P N K I A A (Unsorted list) (Sorted list, ascending) (Sorted list, descending)

Sorting Algorithms 1. Bubble Sort 2. Selection Sort There are few more sorting algorithms; you can find them in a book on data structures and algorithms (or on the Web)

Bubble Sort Algorithm: Informal q Repeatedly compare the elements at consecutive locations in a given list, and do the following until the elements are in required order: § If elements are not in the required order, swap them (change their position) § Otherwise do nothing

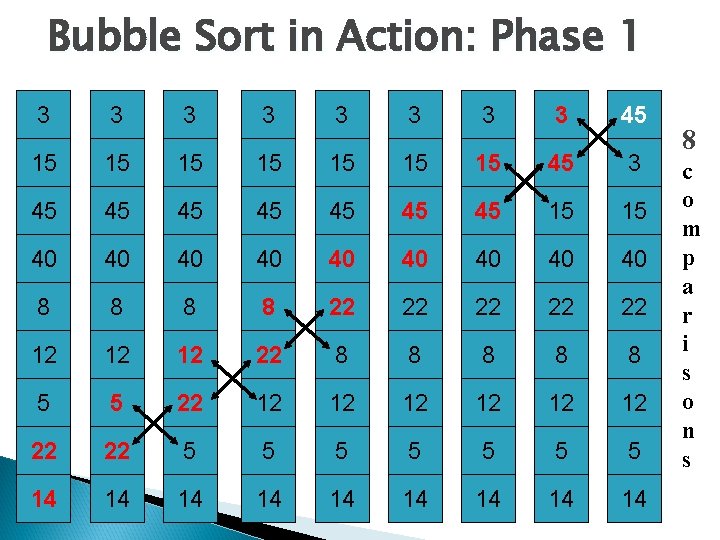
Bubble Sort in Action: Phase 1 3 3 3 3 45 15 15 45 3 45 45 15 15 40 40 40 8 8 22 22 22 12 12 12 22 8 8 8 5 5 22 12 12 12 22 22 5 5 5 5 14 14 14 8 c o m p a r i s o n s

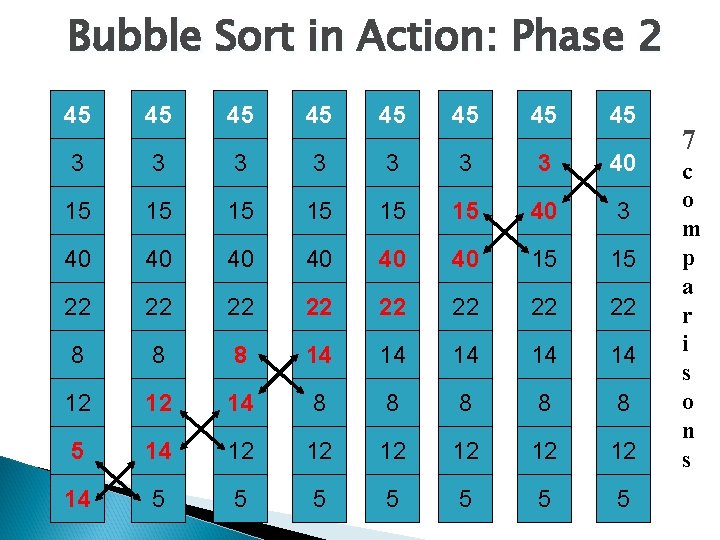
Bubble Sort in Action: Phase 2 45 45 3 3 3 3 40 15 15 15 40 3 40 40 40 15 15 22 22 8 8 8 14 14 14 12 12 14 8 8 8 5 14 12 12 12 14 5 5 5 5 7 c o m p a r i s o n s

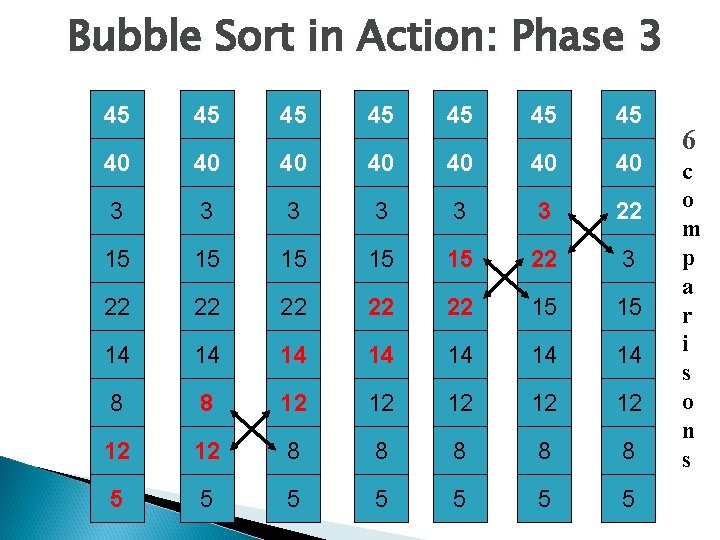
Bubble Sort in Action: Phase 3 45 45 40 40 3 3 3 22 15 15 15 22 3 22 22 22 15 15 14 14 8 8 12 12 8 8 8 5 5 5 5 6 c o m p a r i s o n s

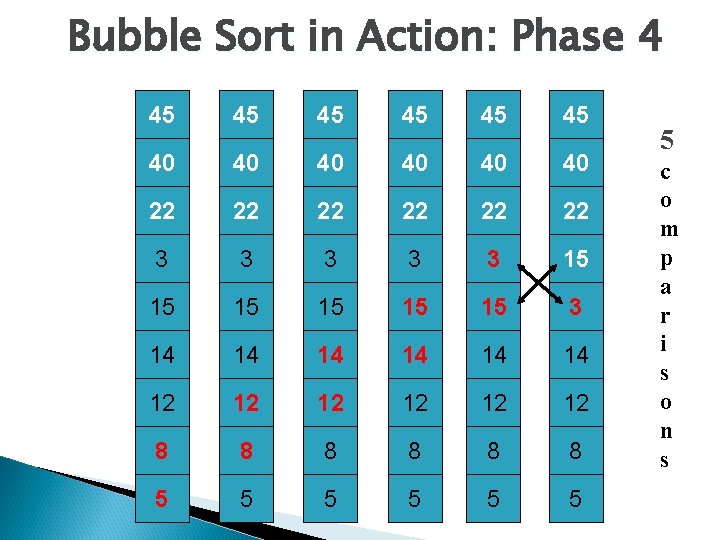
Bubble Sort in Action: Phase 4 45 45 45 40 40 40 22 22 22 3 3 3 15 15 15 3 14 14 14 12 12 12 8 8 8 5 5 5 5 c o m p a r i s o n s

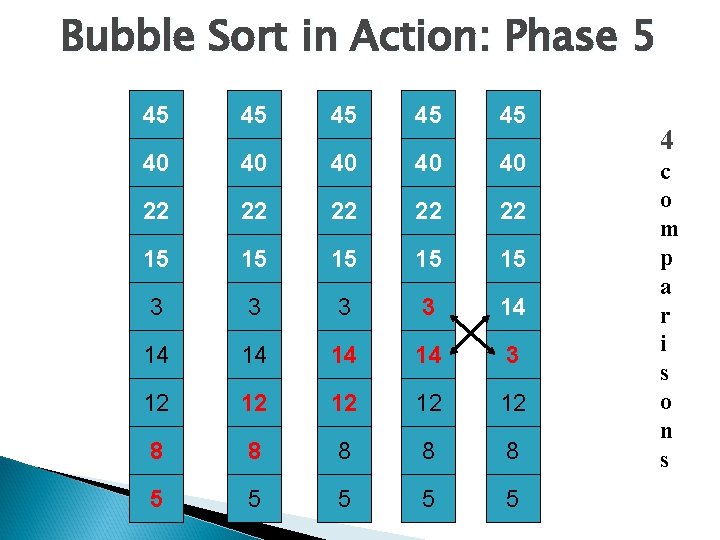
Bubble Sort in Action: Phase 5 45 45 40 40 40 22 22 22 15 15 15 3 3 14 14 14 3 12 12 12 8 8 8 5 5 5 4 c o m p a r i s o n s

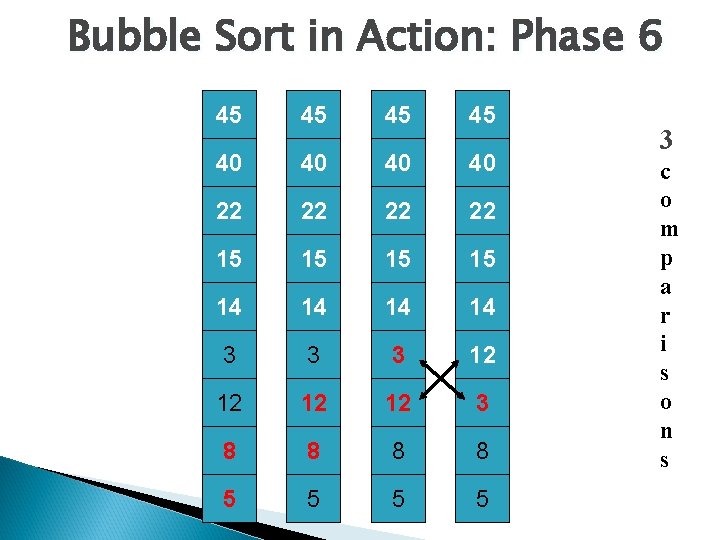
Bubble Sort in Action: Phase 6 45 45 40 40 22 22 15 15 14 14 3 3 3 12 12 3 8 8 5 5 3 c o m p a r i s o n s

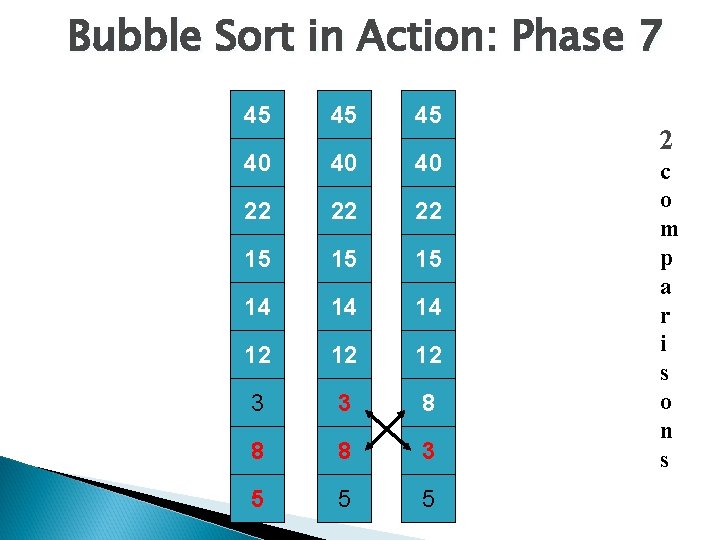
Bubble Sort in Action: Phase 7 45 45 45 40 40 40 22 22 22 15 15 15 14 14 14 12 12 12 3 3 8 8 8 3 5 5 5 2 c o m p a r i s o n s

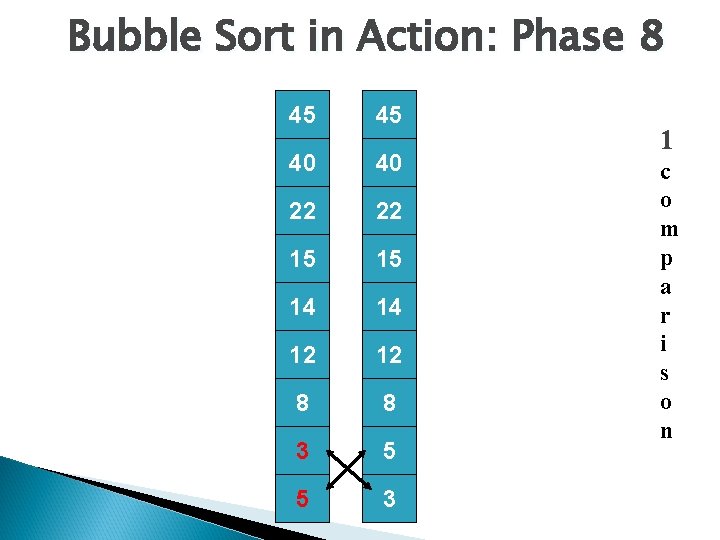
Bubble Sort in Action: Phase 8 45 45 40 40 22 22 15 15 14 14 12 12 8 8 3 5 5 3 1 c o m p a r i s o n

Bubble Sort Algorithm in Java void bubble. Sort(int List[]) { int temp; int size = List. length; for (i = 0; i < size - 1; i++) { for (j = 0; j < size – (i + 1); j++) { if (List[j] > List[j+1]) { //swap temp = List[j]; List[j] = List[j+1]; List[j+1] = temp; } }