Data Structures Binary Tree What is a tree

Data Structures – Binary Tree

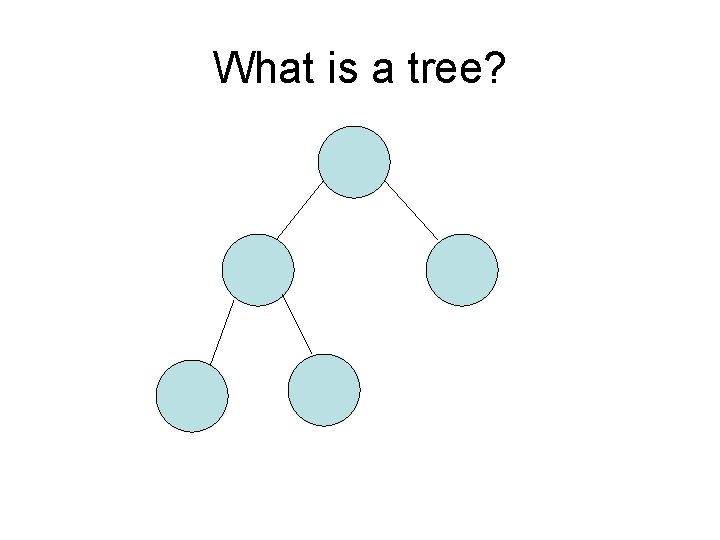
What is a tree?

Where do you see trees? • Ummm. . . outside • Family trees • File systems

Tree Terminology • node – any element of the tree • root – the topmost node of the tree • parent – a node that has one or more nodes connected below it (children) • child – a node that has a connected node above it (parent) • leaf – any child node at the bottom of the tree • subtree – any node and all its descendants

Name that part! root / parent subtree parent / child’ child / leaf

So what’s a binary tree? 1. A parent can have at most TWO children (left child, right child) 2. The left child’s data and all the data in the left subtree is “less than” the parent’s data 3. The right child’s data all the data in the right subtree is “greater than” the parent’s data • NOTE: The “less than” and “greater than” requirements of the subtrees is commonly known outside of the IB world as a Binary Search Tree

Example – Valid Binary Tree 6 2 1 10 4

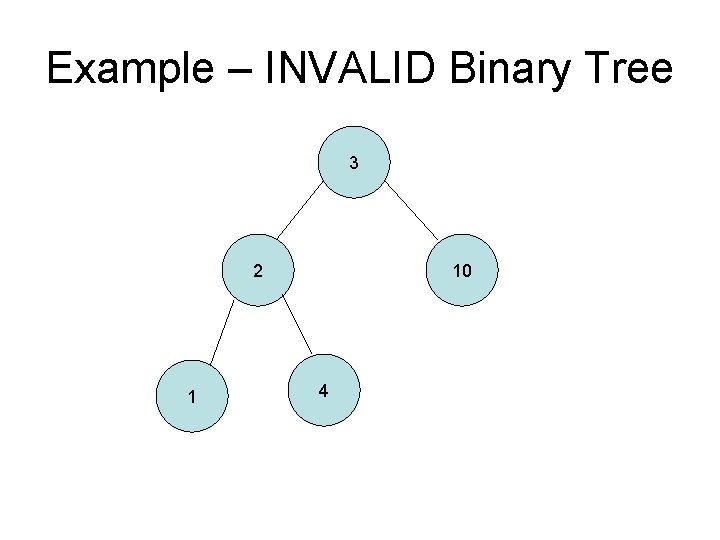
Example – INVALID Binary Tree 3 2 1 10 4

Adding to a Binary Tree 1. Start at the root 2. Compare against the current node 1. Go left if less than current node OR insert if there is none (creating a new leaf) 2. Go right if greater than current node OR insert if there is none (creating a new leaf) 3. Repeat step 2

Creating a binary tree • Insert the following numbers in the given order: 6, 4, 2, 7, 8, 14, 9

Your Turn • Create a binary tree by inserting the following numbers in the given order : 14, 75, 2, 5, 60, 25, 1, 9

Your Turn Again • Create a binary tree by inserting the following numbers in the given order : 2, 4, 6, 8, 10 Notice anything weird? It’s unbalanced!

Another Binary Tree h d a m k x

Practice w/ Strings • Create a binary tree by inserting the following strings: Wanda, Alpos, Vazbyte, Fecso, Downs, Mata, Montante

Searching in a Binary Tree 1. Start at the root 2. Compare against the current node 1. Found the node if they are equal 2. Go left if less than current node OR if there is no left, then does not exist 3. Go right if greater than current node OR if there is no left, then does not exist 3. Repeat step 2

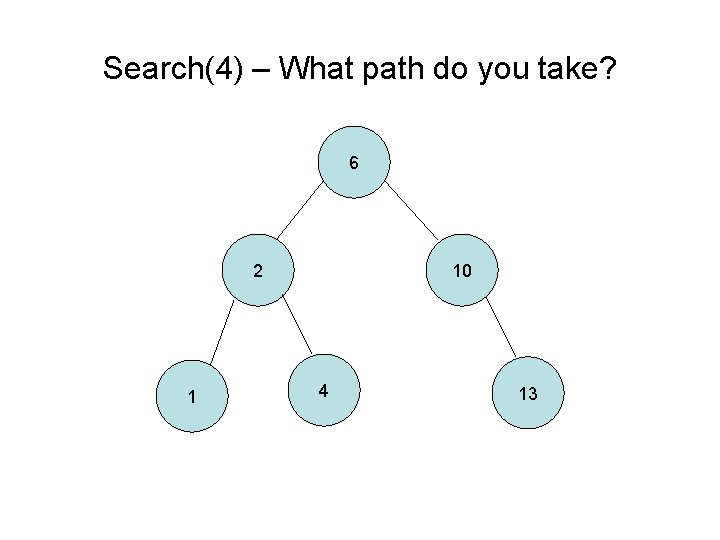
Search(4) – What path do you take? 6 2 1 10 4 13

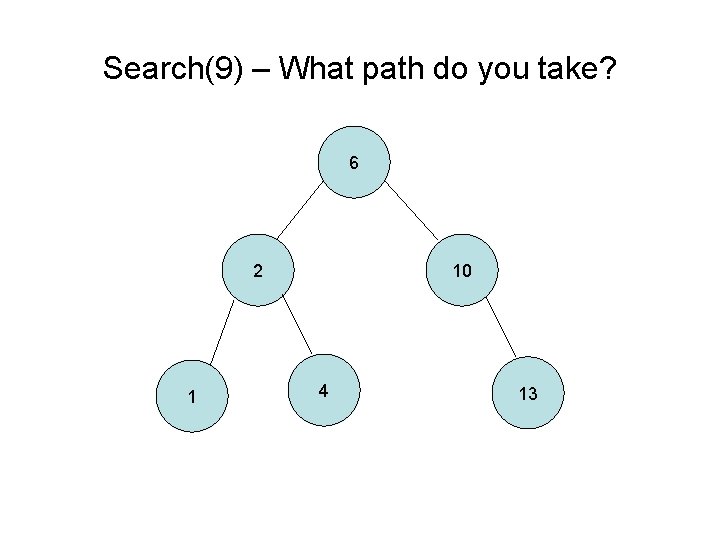
Search(9) – What path do you take? 6 2 1 10 4 13

Removing from a Binary Tree 1. Search for matching node 2. If the node is a leaf (0 children), unlink its parent 3. If the node has 1 child, then link the node’s parent to the node’s child 4. If the node has 2 children, then go to its right subtree and find the left-most child (smallest value of the right subtree). Take the value and put it in the original node that was being removed. Repeat the remove process on the node with 2 children

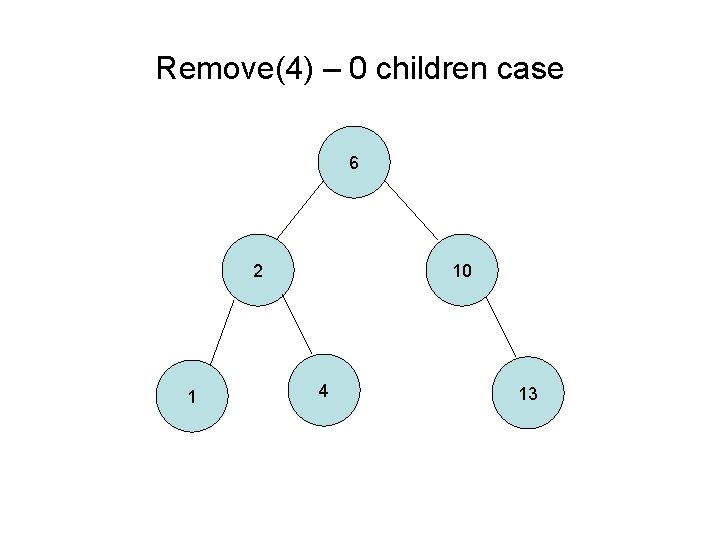
Remove(4) – 0 children case 6 2 1 10 4 13

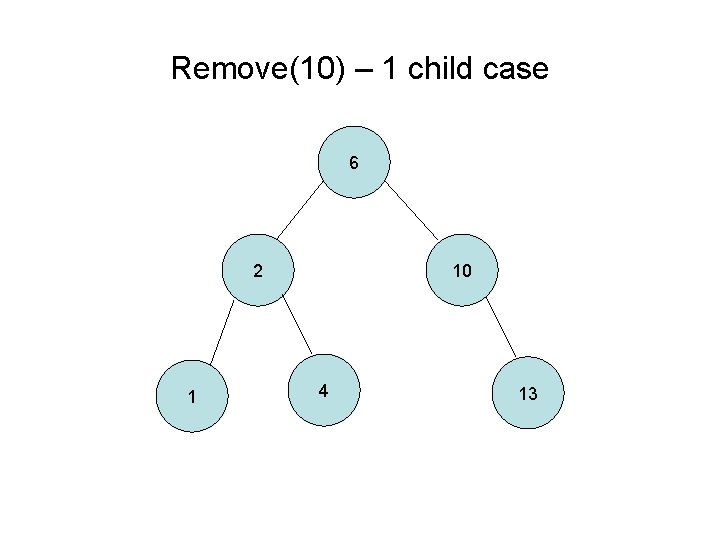
Remove(10) – 1 child case 6 2 1 10 4 13

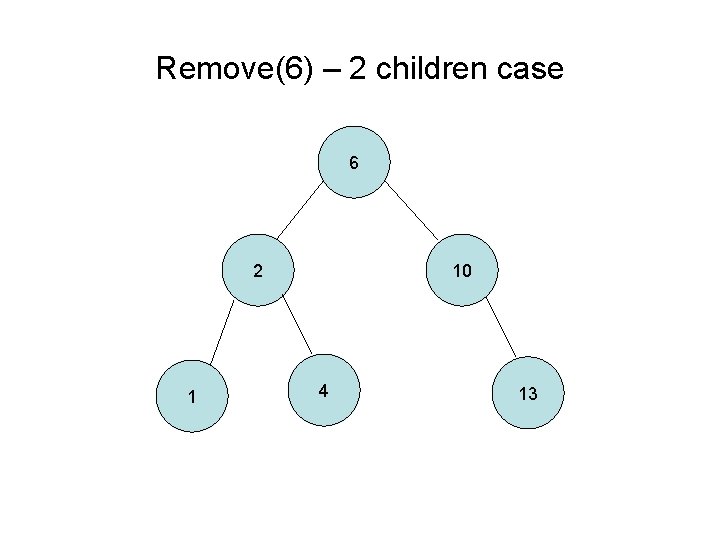
Remove(6) – 2 children case 6 2 1 10 4 13

When do we use binary trees? • . . . whenever we need to search for quickly – Inherent binary searching capabilities – Large trees can be searched quickly • What is the best case scenario? • What is the worst case scenario? – Balanced tree? – Unbalanced tree? • What is the average case scenario? • Compare a Linked List to a Binary Tree

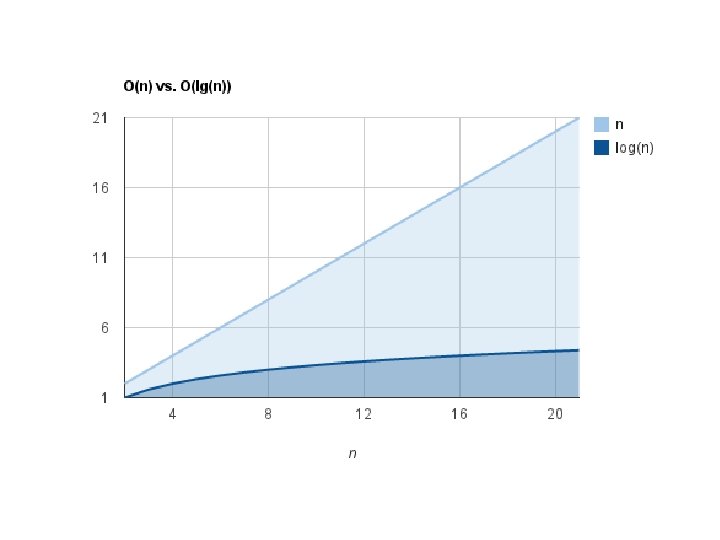
Tree Traversal • Add, remove, search only go down 1 path • How do you “walk-through” all the nodes of a tree?

In-order tree traversal 1. Left-subtree traversal if it exists and rerun 2. Action on the current node (e. g. print) 3. Right-subtree traversal if it exists and rerun Note: In-order traversal often used to visit nodes in their inherent order

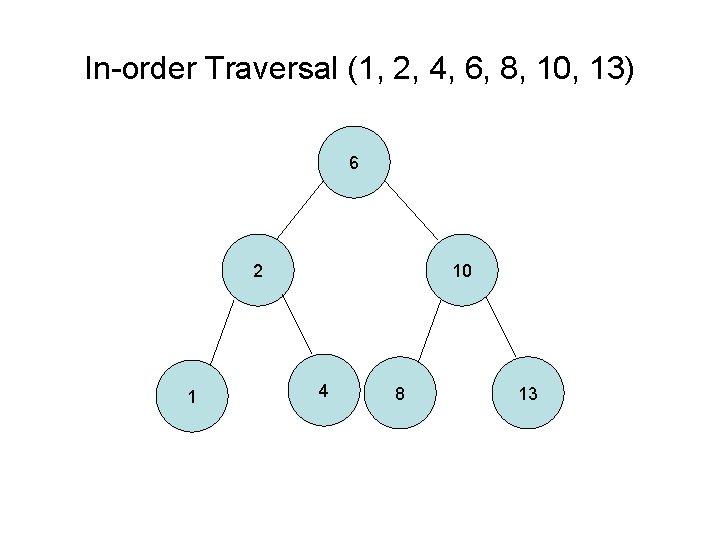
In-order Traversal (1, 2, 4, 6, 8, 10, 13) 6 2 1 10 4 8 13

Pre-order tree traversal 1. Action on the current node (e. g. copy) 2. Left-subtree traversal if it exists and rerun 3. Right-subtree traversal if it exists and rerun Note: Pre-order traversal is often used to duplicate a tree

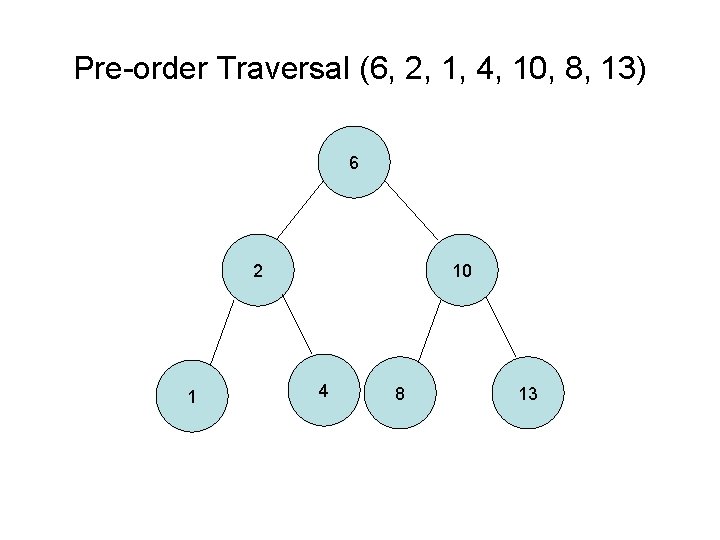
Pre-order Traversal (6, 2, 1, 4, 10, 8, 13) 6 2 1 10 4 8 13

Post-order tree traversal 1. Left-subtree traversal if it exists and rerun 2. Right-subtree traversal if it exists and rerun 3. Action on the current node (e. g. print) Note: Post-order traversal is often used to completely delete or free up all nodes by visiting children and lowest levels first. (not really necessary with garbage collection)

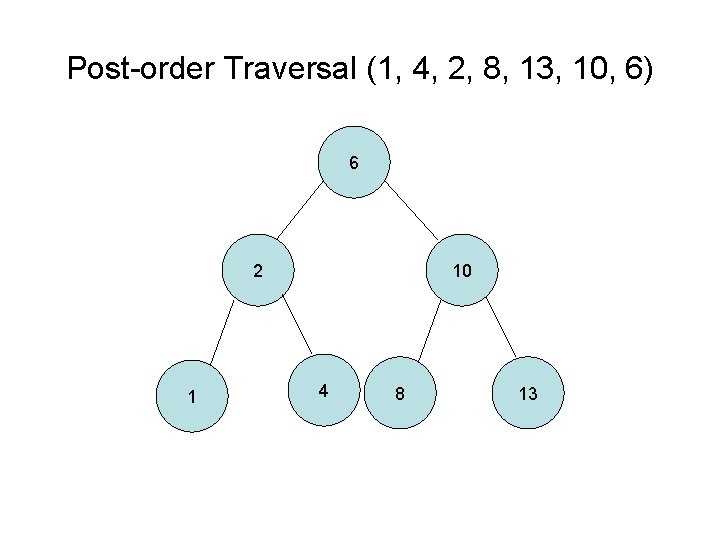
Post-order Traversal (1, 4, 2, 8, 13, 10, 6) 6 2 1 10 4 8 13

Other Resources • http: //www. csanimated. com/animation. php ? t=Binary_search_tree