Data Structures and Image Segmentation Luc Brun L

Data Structures and Image Segmentation Luc Brun L. E. R. I. , Reims University, France and Walter Kropatsch Vienna Univ. of Technology, Austria

Segmentation • Segmentation: Partition of the image into homogeneous connected components S 1 S 2 S 5 S 4 S 3

Segmentation • Problems – Huge amount of data – Homogeneity: • Resolution/Context dependent • Needs – Massive parallelism – Hierarchy

Contents of the talk • Hierarchical Data Structures • Combinatorial Maps • Combinatorial Pyramids

Regular Pyramids

Matrix-Pyramids • Stack of images with progressively reduced resolution 2 x 2/4 Pyramid Level 2 Level 1 Level 0 Level 3

M-Pyramids • M-Pyramid Nx. N/q (Here 2 x 2/4) – Nx. N : Reduction window. Pixels used to compute father’s value (usually low pass filter) – q : Reduction factor. Ratio between the size of two successive images. – Receptive field: set of children in the base level

M-Pyramids • Nx. N/q=1: Non overlapping pyramid without hole (eg. 2 x 2/4) • Nx. N/q<1: Holed Pyramid. • Nx. N/q>1: Overlapping pyramid

Regular Pyramids • Advantages(Bister) – makes the processes independent of the resolution…. • Drawbacks(Bister) : Rigidity – Regular Grid – Fixed reduction window – Fixed decimation ratio

Irregular Pyramids • Stack of successively reduced graphs

Irregular Pyramids [Mee 89, MMR 91, JM 92] • From G=(V, E) to the reduced graph G’=(V’, E’) – Selection of a set of surviving vertices V’ V – Child Parent link Partition of V – Definition of E’ • Selection of Roots

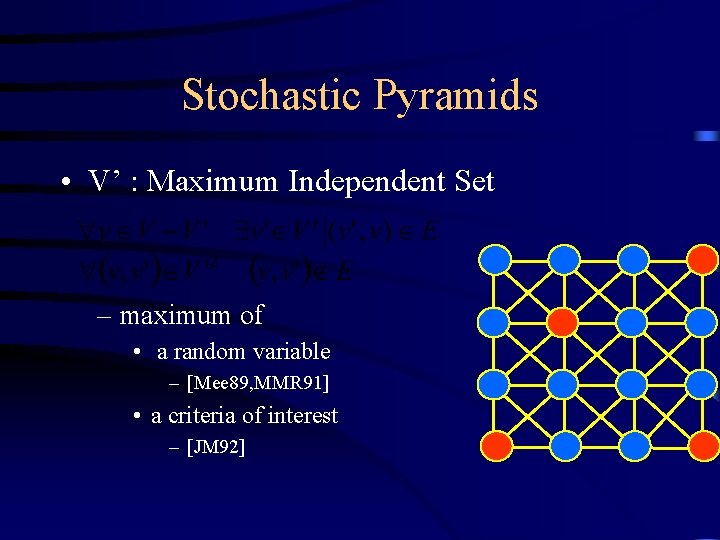
Stochastic Pyramids • V’ : Maximum Independent Set – maximum of • a random variable – [Mee 89, MMR 91] • a criteria of interest – [JM 92]

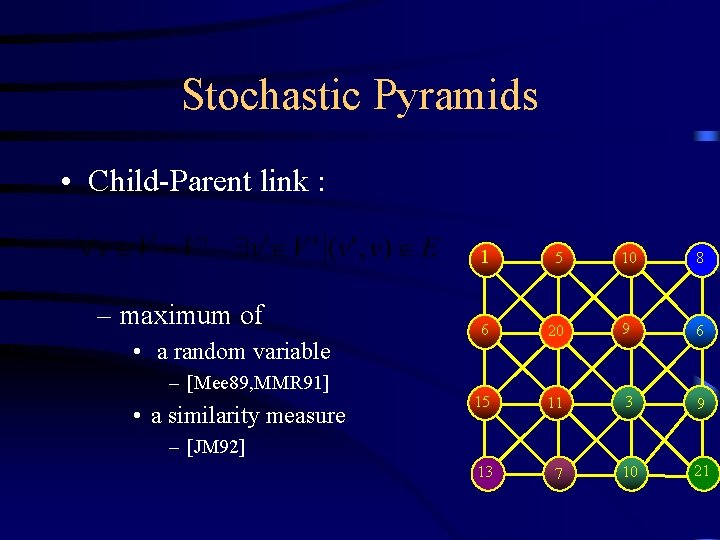
Stochastic Pyramids • Child-Parent link : – maximum of • a random variable – [Mee 89, MMR 91] • a similarity measure 1 5 10 8 6 20 9 6 15 11 3 9 13 7 10 21 – [JM 92]

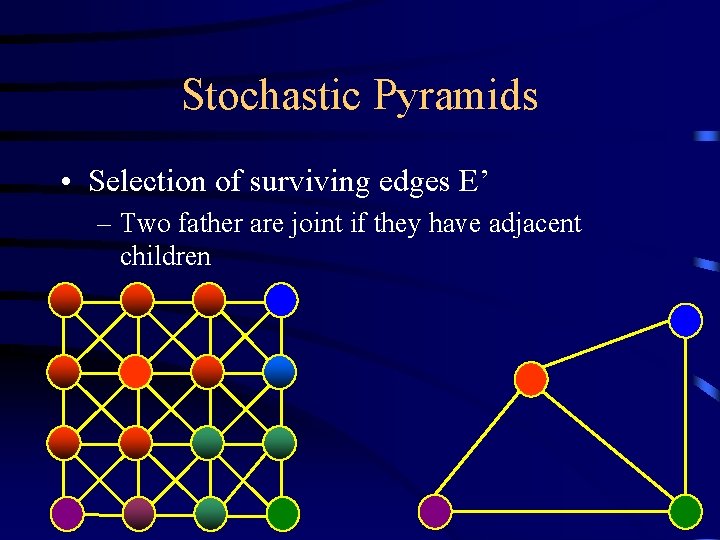
Stochastic Pyramids • Selection of surviving edges E’ – Two father are joint if they have adjacent children

Stochastic Pyramids • Selection of Roots: – Restriction of the decimation process by a class membership function [MMR 91] – contrast measure with legitimate father exceed a threshold [JM 92]

Stochastic Pyramid [MMR 91] • Restriction of the decimation process : Class membership function

Stochastic Pyramids • Advantages – Purely local Processes [Mee 89] – Each root corresponds to a connected region[MMR 91] • Drawback – Rough description of the partition

Formal Definitions Edge Contraction Given an edge to be contracted Identify both vertices Remove the contracted edge

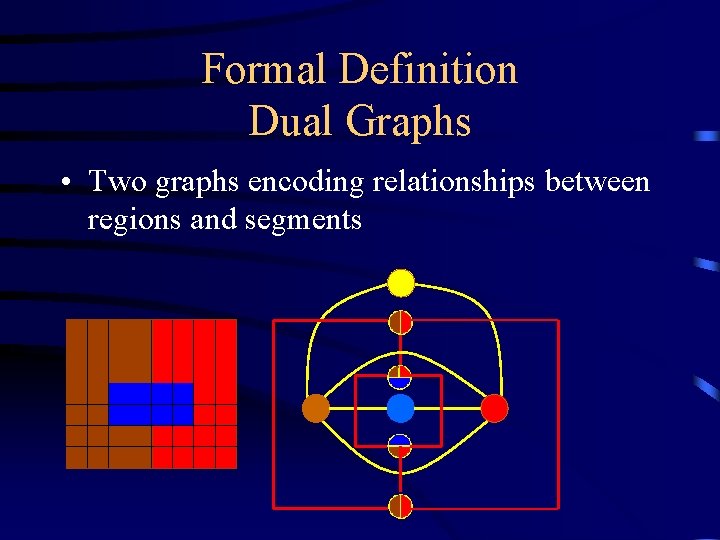
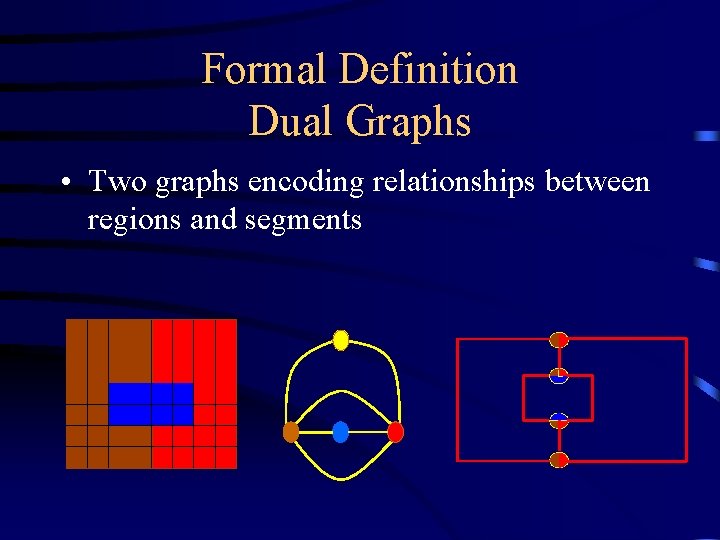
Formal Definition Dual Graphs • Two graphs encoding relationships between regions and segments

Dual Graphs • Advantages (Kropatsch)[Kro 96] – Encode features of both vertices and faces • Drawbacks [BK 00] – Requires to store and to update two data structures • Contraction in G Removal in G • Removal in G Contraction in G

Decimation parameter • Given G=(V, E), a decimation parameter (S, N) is defined by (Kropatsch)[WK 94]: – a set of surviving vertices S V – a set of non surviving edges N E • Every non surviving vertex is connected to a surviving one in a unique way:

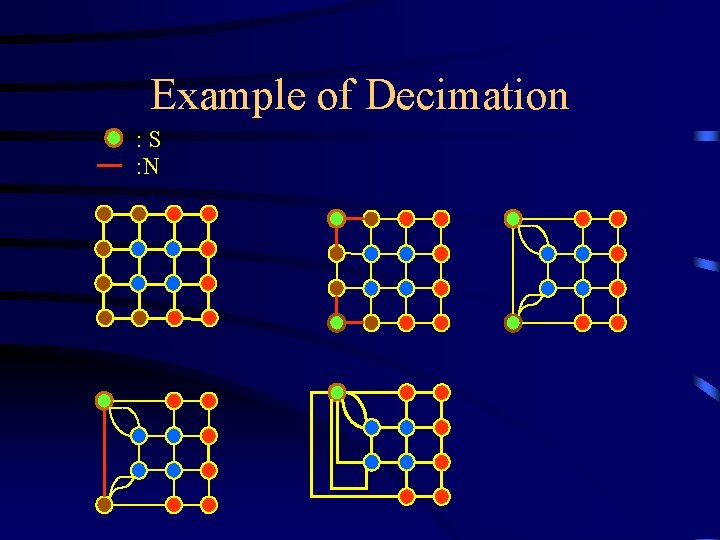
Example of Decimation : S : N

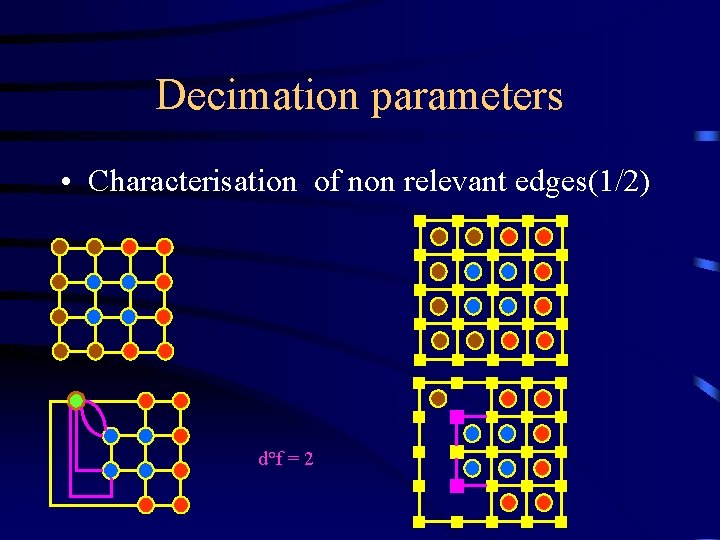
Decimation parameters • Characterisation of non relevant edges(1/2) d°f = 2

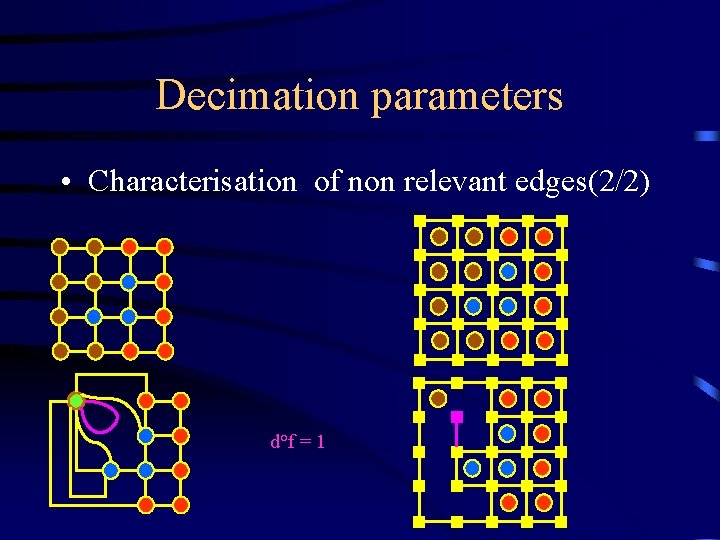
Decimation parameters • Characterisation of non relevant edges(2/2) d°f = 1

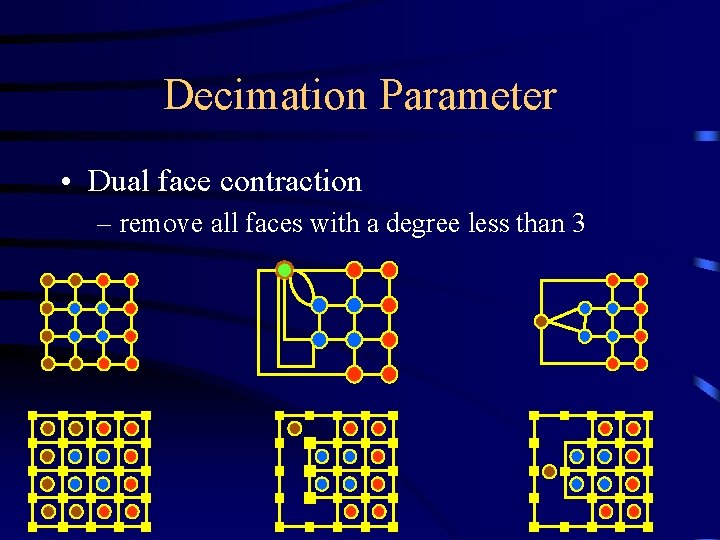
Decimation Parameter • Dual face contraction – remove all faces with a degree less than 3

Decimation Parameter • Edge contraction: Decimation parameter (S, N) – Contractions in G – Removals in G • Dual face contraction : Dual Decimation parameter – Contractions in G – Removals in G

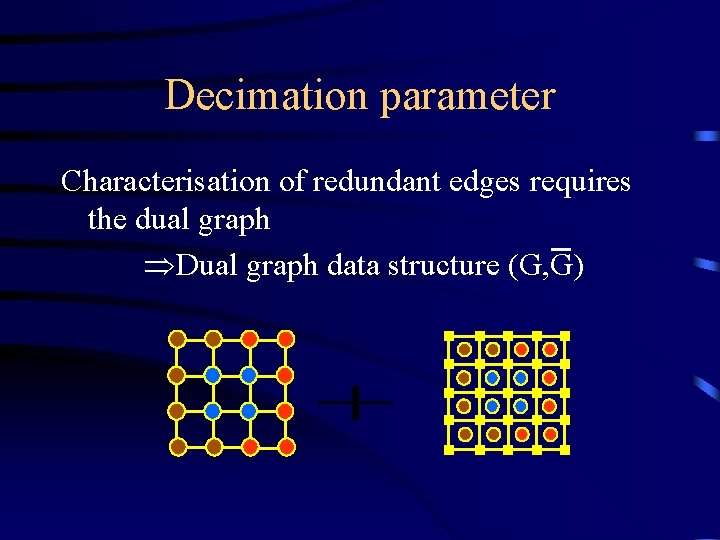
Decimation parameter Characterisation of redundant edges requires the dual graph Dual graph data structure (G, G)

Decimation Parameter • Advantages – Better description of the partition • Drawbacks – Low decimation Ratio

Contraction Kernels Given G=(V, E), a Contraction kernel (S, N) is defined by: – a set of surviving vertices S V – a set of non surviving edges N E Such that: – (V, N) is a forest of (V, E) – Surviving vertices S are the roots of the trees

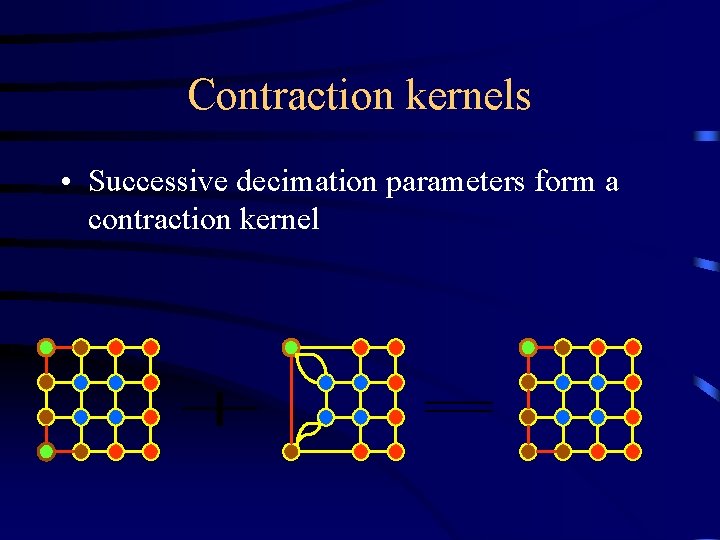
Contraction kernels • Successive decimation parameters form a contraction kernel

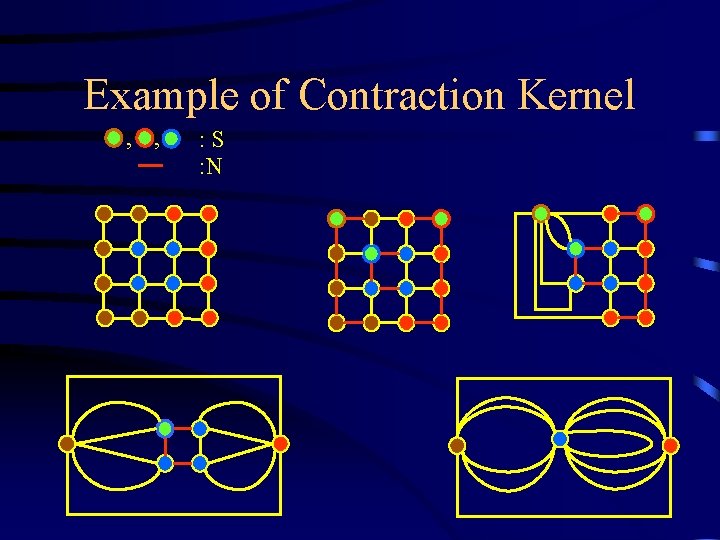
Example of Contraction Kernel , , : S : N

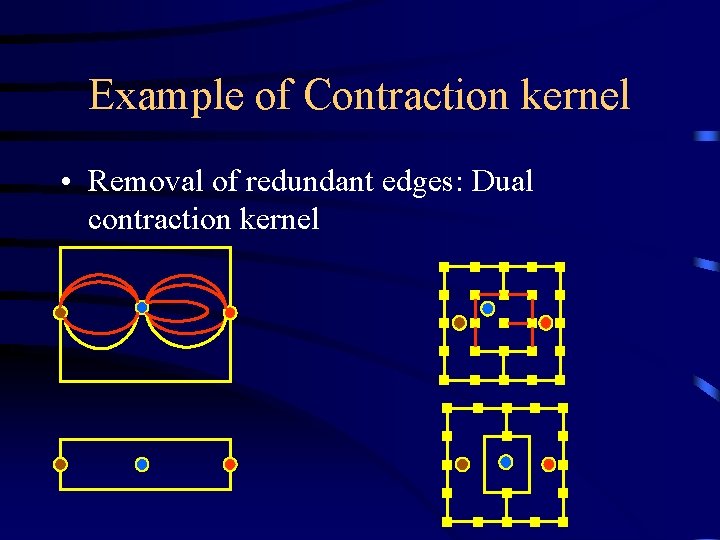
Example of Contraction kernel • Removal of redundant edges: Dual contraction kernel

Hierarchical Data Structures / Combinatorial Maps • M-Pyramids • Overlapping Pyramids • Stochastic Pyramids • Adaptive Pyramids • Decimation parameter • Contraction kernel

Combinatorial Maps Definition • G=(V, E) G=(D, , ) – decompose each edge into two half-edges(darts) : D ={-6, …, -1, 1, …, 6} - : edge encoding -2 -6 -5 6 -1 -4 5 -3 3 4 2 1

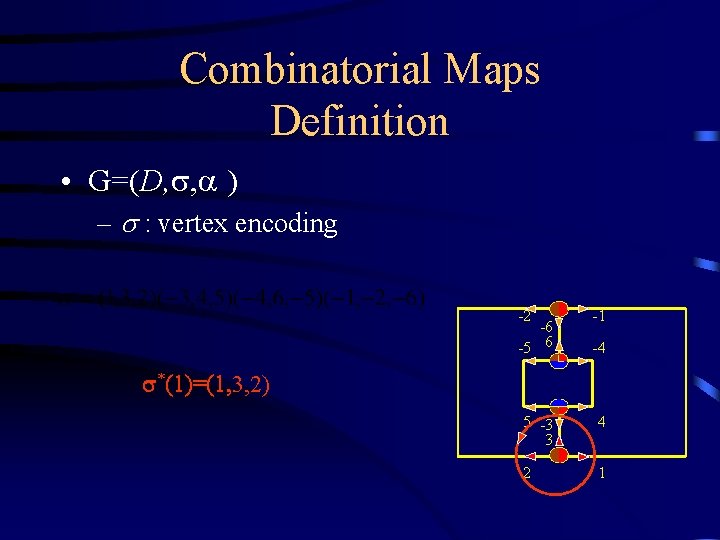
Combinatorial Maps Definition • G=(D, , ) – : vertex encoding -2 -6 -5 6 -1 -4 (1)=(1, 3 *(1)=(1, 3, 2) 5 -3 3 4 2 1

Combinatorial Maps Properties • Computation of the dual graph : – G=(D, , ) G=(D, = , ) 1 -2 2 -3 -5 5 *(-1)=(-1, 3, 4, 6) (-1)=(-1, 3, 4 (-1)=(-1, -6 3 -1 -4 4 6 • The order defined on induces an order on

Combinatorial Maps Properties • Computation of the dual graph : – G=(D, , ) G=(D, = , ) (-1)=(-1, 3, 4 (-1)=(-1, *(-1)=(-1, 3, 4, 6) -2 -6 -5 6 -1 -4 5 -3 3 4 2 1

Combinatorial Maps Properties • Summary – The darts are ordered around each vertex and face • The boundary of each face is ordered • The set of regions which surround an other one is ordered – The dual graph may be implicitly encoded – Combinatorial maps may be extended to higher dimensions (Lienhardt)[Lie 89]

Combinatorial Maps/Combinatorial Pyramids • Combinatorial Maps • Computation of Dual Graphs • Combinatorial Maps properties • Discrete Maps [Bru 99] http: //www. univ-st-etienne. fr/iupvis/color/Ecole-Ete/Brun. ppt

Removal operation • G=(D, , ) – d D such that d is not a bridge • G’=G *(d)=(D’, ) d -d

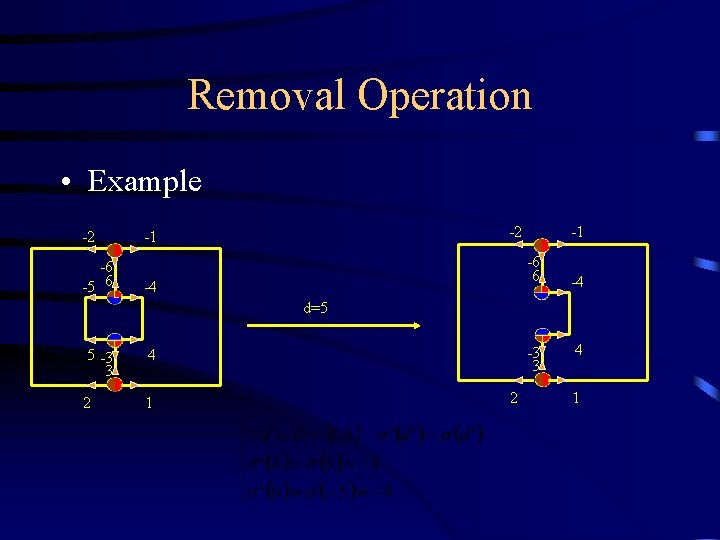
Removal Operation • Example -2 -6 -5 6 -2 -1 -1 -6 6 -4 -4 d=5 5 -3 3 4 2 1 -3 3 2 4 1

Contraction operations • G=(D, , ) – d D such that d is not a self-loop • G’=G/ *(d)=(D’, ) d -d

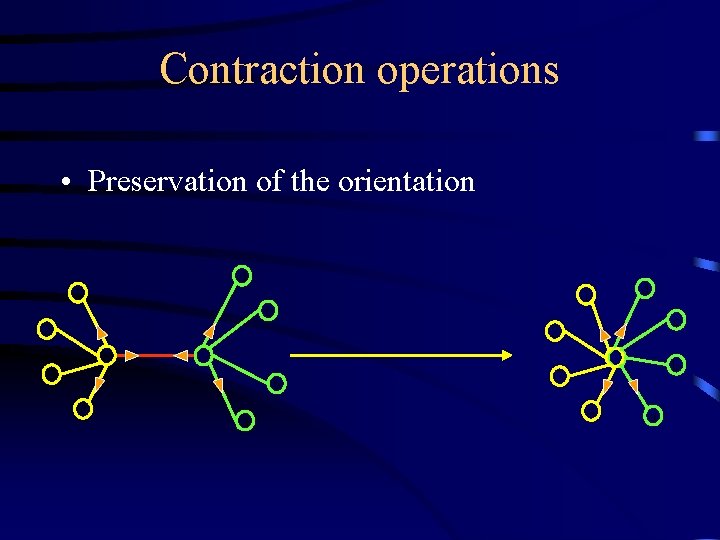
Contraction operations • Preservation of the orientation 1 d 1 c 2 d c 2 3 b 4 a b 3 4 a

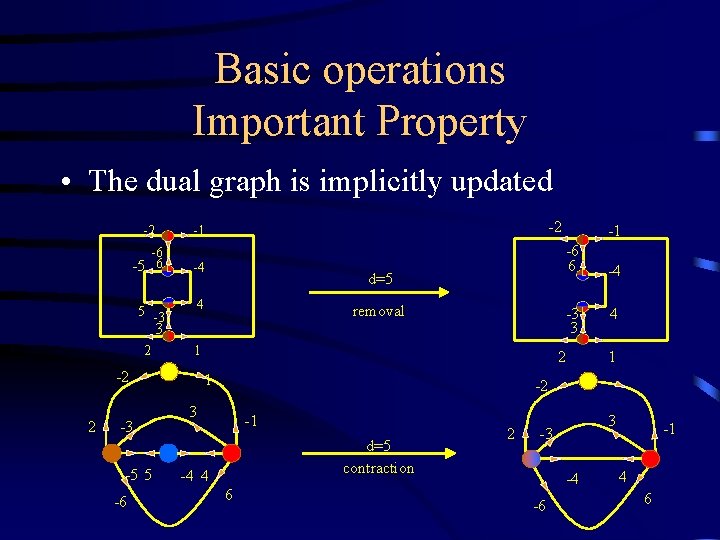
Basic operations Important Property • The dual graph is implicitly updated -2 -2 -1 -6 -5 6 -4 5 -3 4 2 1 -6 6 d=5 removal -3 3 3 -2 2 -3 -5 5 -6 -1 2 1 -4 4 1 -2 3 -1 d=5 contraction -4 4 6 2 3 -3 -4 -6 -1 4 6

Contraction Kernel • Given G=(D, , ), K D is a contraction kernel iff: – K is a forest of G • Symmetric set of darts ( (K)=K) • Each connected component is a tree – Some surviving darts must remain • SD=D-K

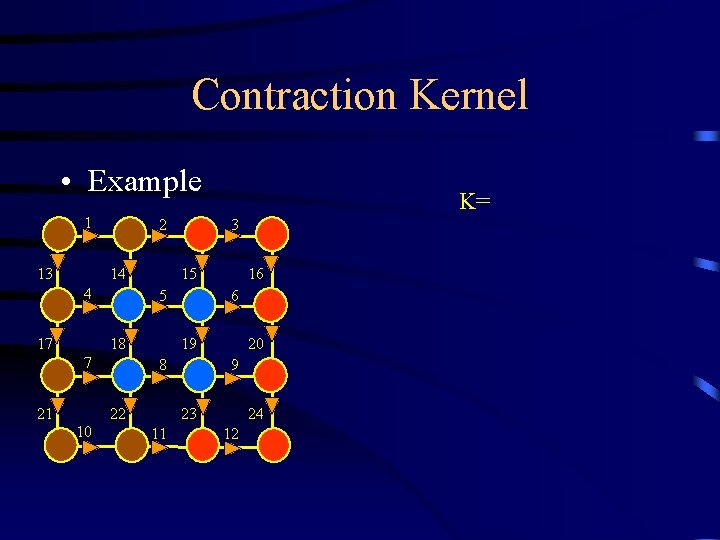
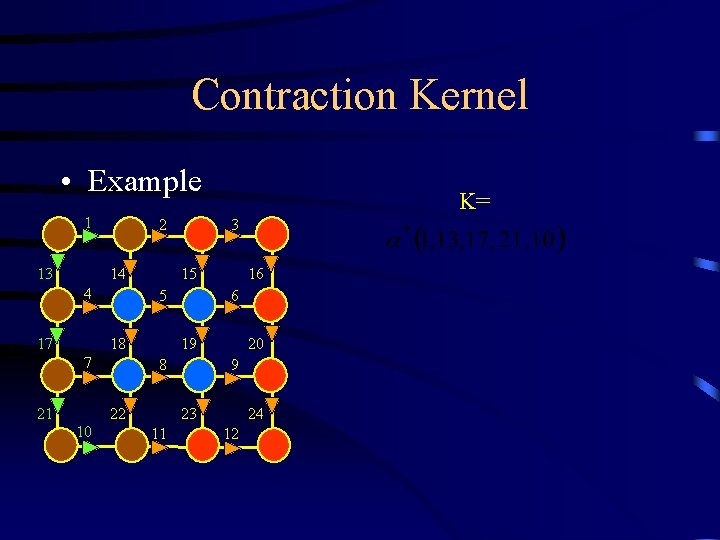
Contraction Kernel • Example 1 13 2 14 4 17 21 15 18 10 3 5 7 K= 16 6 19 8 22 20 9 23 11 24 12

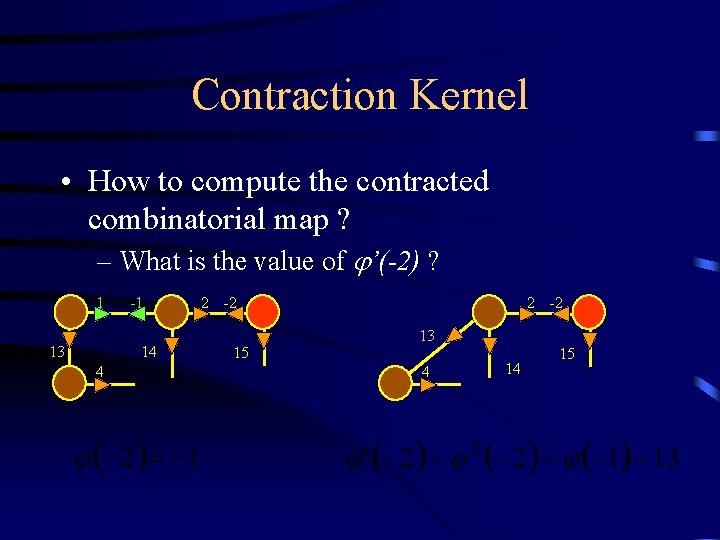
Contraction Kernel • How to compute the contracted combinatorial map ? – What is the value of ’(-2) ? 1 13 -1 14 4 2 -2 13 15 4 14 15

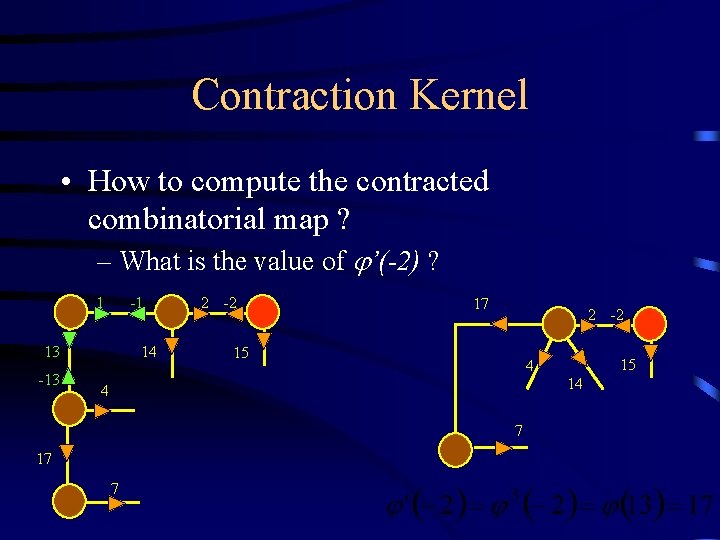
Contraction Kernel • How to compute the contracted combinatorial map ? – What is the value of ’(-2) ? 1 -1 13 -13 14 2 -2 17 2 -2 15 15 4 14 4 7 17 7

Contraction Kernel • Connecting Walk – Given G=(D, , ) , K D and SD=D-K – If d SD, CW(d) is the minimal sequence of non surviving darts between d and a surviving one. • The connecting walks connect the surviving darts.

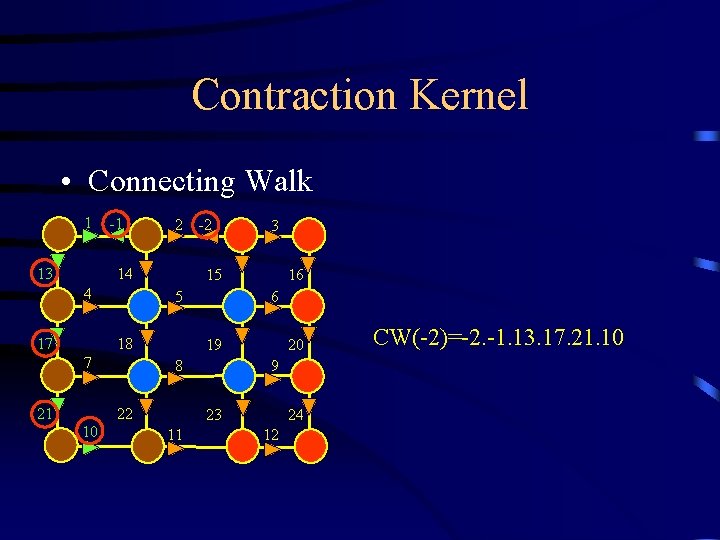
Contraction Kernel • Connecting Walk 1 13 -1 14 4 17 18 10 3 15 5 7 21 2 -2 16 6 19 8 22 20 9 23 11 24 12 CW(-2)=-2. -1. 13. 17. 21. 10

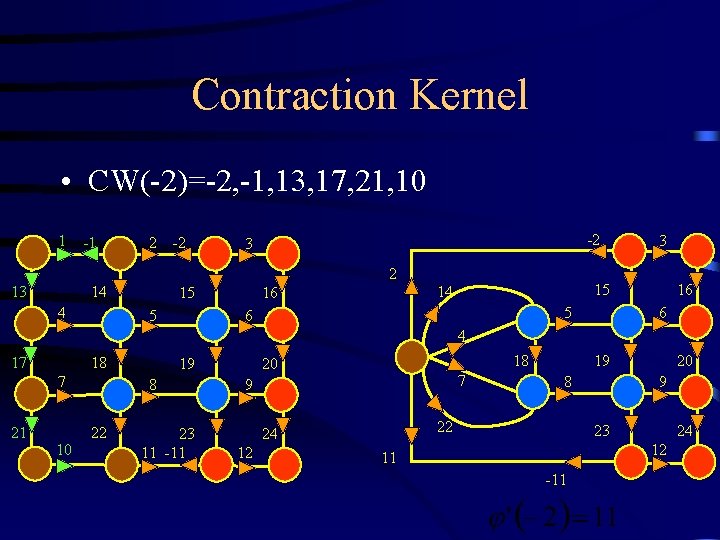
Contraction Kernel • CW(-2)=-2, -1, 13, 17, 21, 10 1 -1 2 -2 -2 3 2 13 14 4 15 5 15 14 16 3 5 6 16 6 4 17 18 7 21 10 19 8 22 23 11 -11 7 9 8 22 24 12 19 18 20 20 9 23 24 12 11 -11

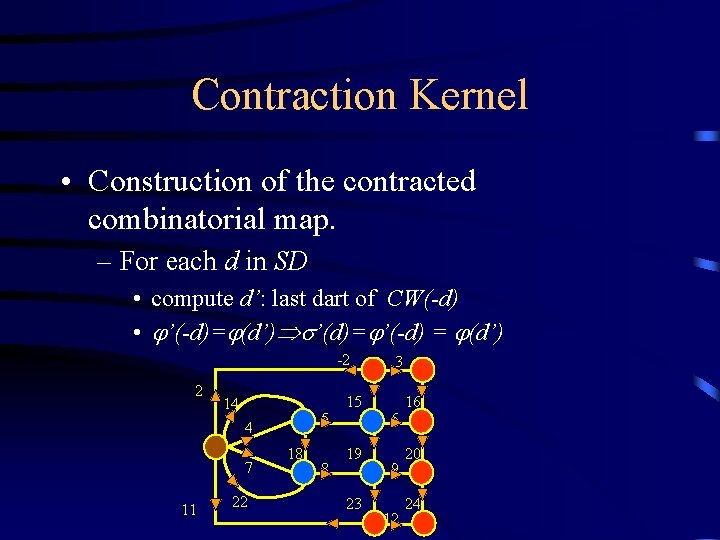
Contraction Kernel • Construction of the contracted combinatorial map. – For each d in SD • compute d’: last dart of CW(-d) • ’(-d)= (d’) ’(d)= ’(-d) = (d’) -2 2 14 5 4 7 11 22 18 8 15 19 23 3 6 9 12 16 20 24

Extensions (1/2) • Dual contraction kernel – Replace by • Successive Contraction kernels with a same type – Concatenation of connecting walks

Extensions (2/2) • Successive contraction kernels with different types – From connecting walks to Connecting Dart Sequences • Label Pyramids: – for each dart encode • Its maximum level in the pyramid (life time) • How its disappear (contracted or removed)

Conclusion • Graphs encode efficiently topological features. Combinatorial maps: – Encode the orientation – Provide an implicit encoding of the dual – May be generalised to higher dimension • Irregular Pyramids overcome the limitations of their regular ancestors Combinatorial Pyramids