Data Structures and Algorithms Sorting AlgorithmsI Data Structure

Data Structures and Algorithms Sorting Algorithms(I) Data Structure _ Sem 4_ICT& CS Lecture 4 Ms. Hiba Sayed

Introduction to Sorting Algorithms • Sort: arrange values into an order: – Alphabetical – Ascending numeric – Descending numeric • There are many different types of sorting algorithms, but the primary ones are: – – – Bubble Sort Selection Sort Insertion Sort Merge Sort Quick Sort – – Bubble sort Selection sort Insertion sort Quick Sort • Four algorithms considered here:

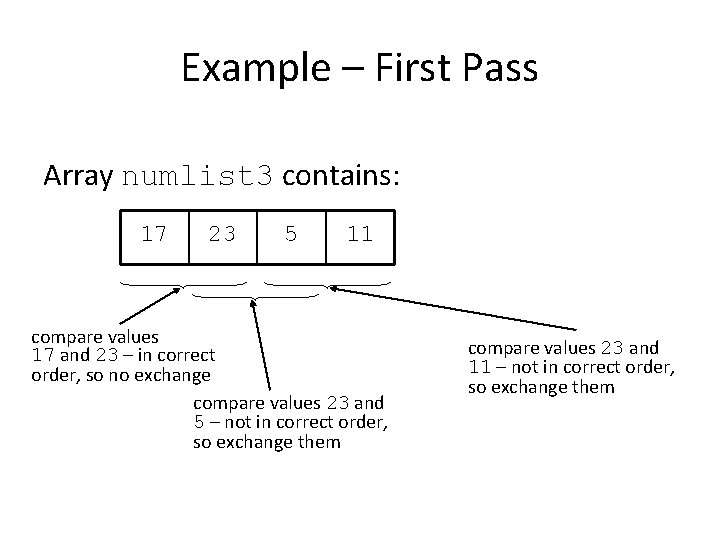
Bubble Sort Bubble sort is a simple sorting algorithm, orders a list of values by repetitively comparing neighboring elements and swapping their positions if necessary Concept: – Compare 1 st two elements • If out of order, exchange them to put in order – Move down one element, compare 2 nd and 3 rd elements, exchange if necessary. Continue until end of array. – Pass through array again, exchanging as necessary – Repeat until pass made with no exchanges

Example – First Pass Array numlist 3 contains: 17 23 5 11 compare values 17 and 23 – in correct order, so no exchange compare values 23 and 5 – not in correct order, so exchange them compare values 23 and 11 – not in correct order, so exchange them

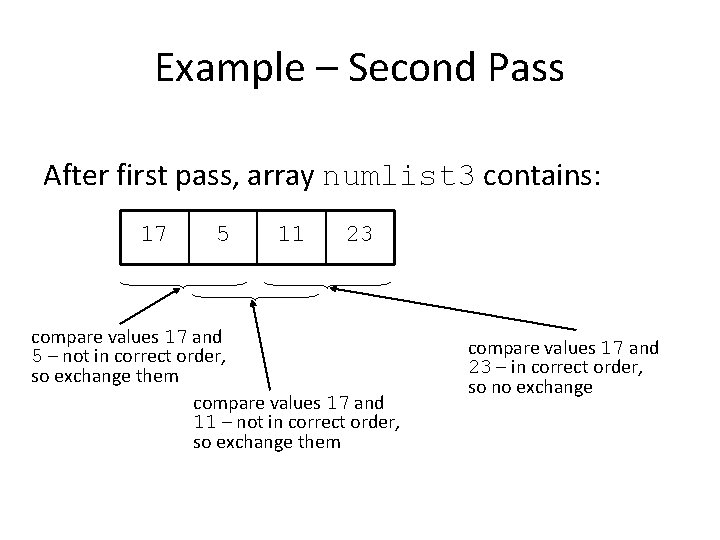
Example – Second Pass After first pass, array numlist 3 contains: 17 5 11 23 compare values 17 and 5 – not in correct order, so exchange them compare values 17 and 11 – not in correct order, so exchange them compare values 17 and 23 – in correct order, so no exchange

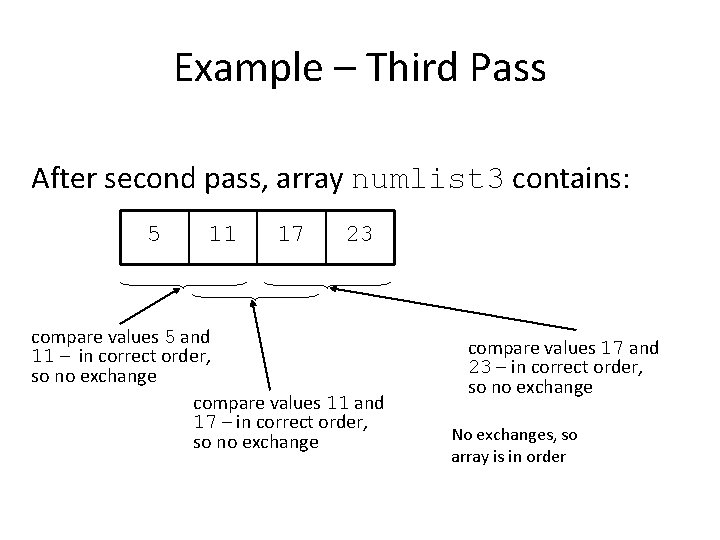
Example – Third Pass After second pass, array numlist 3 contains: 5 11 17 23 compare values 5 and 11 – in correct order, so no exchange compare values 11 and 17 – in correct order, so no exchange compare values 17 and 23 – in correct order, so no exchange No exchanges, so array is in order

Algorithm Bubble Sort (numlist 3, N element): for i : = 1 to N-1 do { for j : = 0 to N-i-1 do { if (numlist 3 [j] > numlist 3 [j+1] ) { temp : = numlist 3 [j]; numlist 3 [j] : = numlist 3 [j+1]; numlist 3 : = temp ; } } }

A Bubble Sort Function Exercise: Rewrite Bubble_Sort( ) function using for loop , while loop and using Temp() function

Bubble Sort - Tradeoffs • Benefit: – Easy to understand implement • Disadvantage: – Inefficient: slow for large arrays

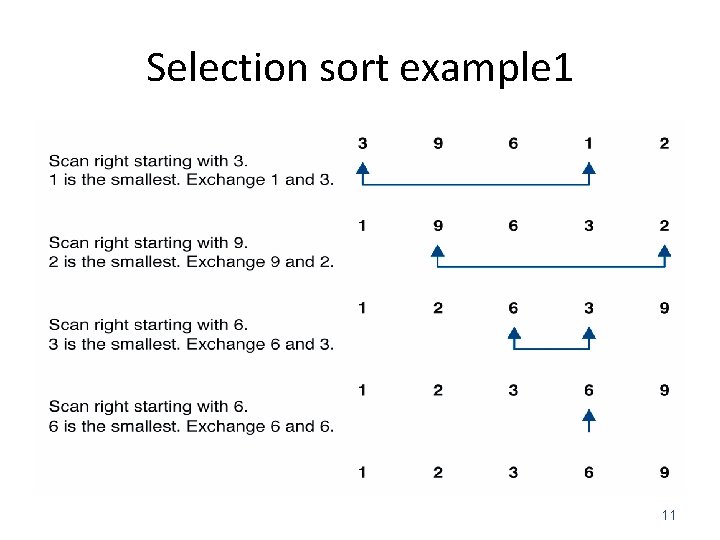
Selection Sort • Selection sort is a good algorithm to sort small number of elements, orders a list of values by repetitively putting a particular value into its final position • Concept for sort in ascending order: – Find the smallest value in the array. – Locate smallest element in array. Exchange it with element in position 0 – Locate next smallest element in array. Exchange it with element in position 1. – Continue until all elements are arranged in order

Selection sort example 1 11

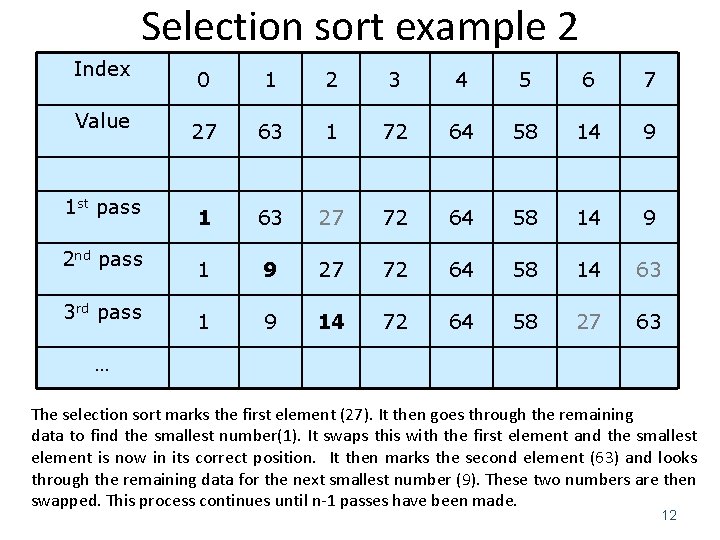
Selection sort example 2 Index Value 1 st pass 2 nd pass 3 rd pass 0 1 2 3 4 5 6 7 27 63 1 72 64 58 14 9 1 63 27 72 64 58 14 9 1 9 27 72 64 58 14 63 1 9 14 72 64 58 27 63 … The selection sort marks the first element (27). It then goes through the remaining data to find the smallest number(1). It swaps this with the first element and the smallest element is now in its correct position. It then marks the second element (63) and looks through the remaining data for the next smallest number (9). These two numbers are then swapped. This process continues until n-1 passes have been made. 12

Selection Sort – Example 3 Array numlist contains: 11 2 29 3 1. Smallest element is 2. Exchange 2 with element in 1 st position in array: 2 11 29 3

Example 3 (Continued) 2. Next smallest element is 3. Exchange 3 with element in 2 nd position in array: 2 3 29 11 3. Next smallest element is 11. Exchange 11 with element in 3 rd position in array: 2 3 11 29

A Selection Sort Function void Selection_Sort(int array[], int size) { int i, min. Index, min. Value; for (i = 0; i < (size - 1); i++) { min. Index = i; min. Value = array[i]; for(int index = i + 1; index < size; index++) { if (array[index] < min. Value) { min. Value = array[index]; min. Index = index; } } array[min. Index] = array[i]; array[i] = min. Value; Exercise: Rewrite Selection_Sort( } } using, while loop. ) function

Selection Sort - Tradeoffs • Benefit: – More efficient than Bubble Sort, since fewer exchanges • Disadvantage: – May not be as easy as Bubble Sort to understand