DATA STRUCTURES AND ALGORITHMS ROAD MAP What is

DATA STRUCTURES AND ALGORITHMS

ROAD MAP �What is an algorithm ? �What is a data structure ? �Analysis of An Algorithm �Asymptotic Notations �Big Oh Notation �Omega Notation �Theta Notation �Little o Notation �Rules about Asymptotic Notations 2

What is An Algorithm ? �Definition : A finite, clearly specified sequence of instructions to be followed to solve a problem. 3

What is An Algorithm ? Problem : Write a program to calculate int Sum (int N) Partial. Sum 0 i 1 int Sum (int N) { int Partial. Sum = 0 ; for (int i=1; i<=N; i++) Partial. Sum += i * i; foreach (i > 0) and (i<=N) Partial. Sum + (i*i*i) increase i with 1 return value of Partial. Sum return Partial. Sum; } 4

Properties of an Algorithm �Effectiveness �simple �can be carried out by pen and paper �Definiteness �clear �meaning is unique �Correctness �give the right answer for all possible cases �Finiteness �stop in reasonable time 5

Is function F an algorithm? int F (int m) { n = m; while (n>1) { if (n/2 == 0) n=n/2; else n=3*n+1; } return m; } 6

What is a Data Structure ? �Definition : An organization and representation of data �representation � data can be stored variously according to their type � signed, unsigned, etc. � example : integer representation in memory �organization � the way of storing data changes according to the organization � ordered, inordered, tree � example : if you have more then one integer ? 7

Properties of a Data Structure ? �Efficient utilization of medium �Efficient algorithms for �creation �manipulation (insertion/deletion) �data retrieval (Find) �A well-designed data structure allows using little �resources �execution time �memory space 8

The Process of Algorithm Development �Design �divide&conquer, greedy, dynamic programming �Validation �check whether it is correct �Analysis �determine the properties of algorithm �Implementation �Testing �check whether it works for all possible cases 9

Analysis of Algorithm �Analysis investigates �What are the properties of the algorithm? � in terms of time and space �How good is the algorithm ? � according to the properties �How it compares with others? � not always exact �Is it the best that can be done? � difficult ! 10

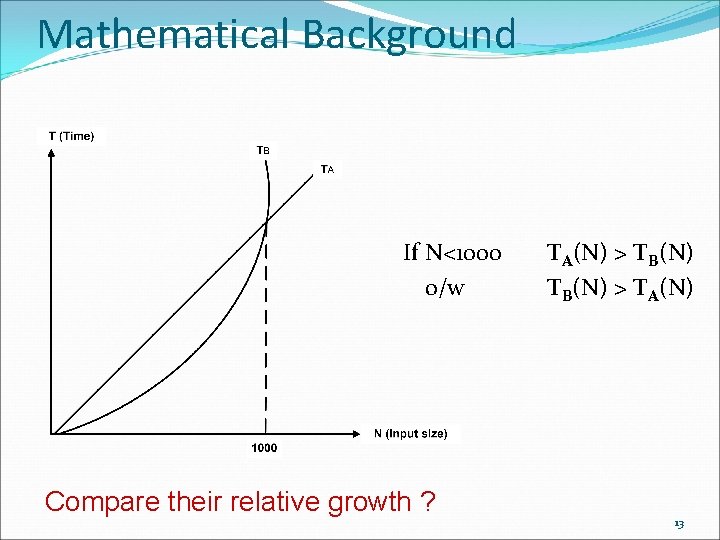
Mathematical Background �Assume the functions for running times of two algorthms are found ! For input size N Running time of Algorithm A = TA(N) = 1000 N Running time of Algorithm B = TB(N) = N 2 Which one is faster ? 11

Mathematical Background If the unit of running time of algorithms A and B is µsec N 10 TA 10 -2 sec TB 10 -4 sec 100 10 -1 sec 10 -2 sec 1000 1 sec 10000 10 sec 100000 100 sec 10000 sec So which algorithm is faster ? 12

Mathematical Background If N<1000 o/w Compare their relative growth ? TA(N) > TB(N) > TA(N) 13

Mathematical Background �Is it always possible to have definite results? NO ! The running times of algorithms can change because of the platform, the properties of the computer, etc. We use asymptotic notations (O, Ω, θ, o) � compare relative growth � compare only algorithms 14

Big Oh Notation (O) Provides an “upper bound” for the function f �Definition : T(N) = O (f(N)) if there are positive constants c and n 0 such that T(N) ≤ cf(N) when N ≥ n 0 �T(N) grows no faster than f(N) �growth rate of T(N) is less than or equal to growth rate of f(N) for large N �f(N) is an upper bound on T(N) � not fully correct ! 15

Big Oh Notation (O) Analysis of Algorithm A 1000 N ≤ c. N if c= 2000 and n 0 = 1 for all N is right 16

Examples � 7 n+5 = O(n) for c=8 and n 0 =5 7 n+5 ≤ 8 n n>5 = n 0 � 7 n+5 = O(n 2) for c=7 and n 0=2 7 n+5 ≤ 7 n 2 n≥n 0 � 7 n 2+3 n = O(n) ? 17

Advantages of O Notation �It is possible to compare of two algorithms with running times �Constants can be ignored. �Units are not important O(7 n 2) = O(n 2) �Lower order terms are ignored �O(n 3+7 n 2+3) = O(n 3) 18

Running Times of Algorithm A and B TA(N) = 1000 N = O(N) TB(N) = N 2 = O(N 2) A is asymptotically faster than B ! 19

Omega Notation (Ω) Definition : T(N) = Ω (f(N)) if there are positive constants c and n 0 such that T(N) ≥ c f(N) when N≥ n 0 T(N) grows no slower than f(N) growth rate of T(N) is greater than or equal to growth rate of f(N) for large N f(N) is a lower bound on T(N) not fully correct ! 20

Omega Notation Example: �n 1/2 = W )lg n. ( for c = 1 and n 0 = 16 Let n > 16 c*(lg n) ≤ n 1/2 21

Omega Notation �Theorem: f(N) = O(g(n)) <=> g(n) = Ω(f(N)) Proof: f(N) ≤ c 1 g(n) <=> g(n) ≥ c 2 f(N) divide the left side with c 1 1/c 1 f(N) ≤ g(n) <=> g(n) ≥ c 2 f(N) if we choose c 2 as 1/c 1 then theorem is right. 22

Omega Notation � 7 n + 3 n + 5 = O(n ) 2 4 � 7 n 2 + 3 n + 5 = O(n 3) � 7 n 2 + 3 n + 5 = O(n 2) � 7 n 2 + 3 n + 5 = Ω(n) � 7 n 2 + 3 n + 5 = Ω(1) n 2 and 7 n 2 + 3 n + 5 grows at the same rate 7 n 2 + 3 n + 5 = O(n 2) = Ω(n 2) = θ (n 2) 23

Theta Notation (θ) �Definition : T(N) = θ (h(N)) if and only if T(N) = O(h(N)) and T(N) = Ω(h(N)) �T(N) grows as fast as h(N) �growth rate of T(N) and h(N) are equal for large N �h(N) is a tight bound on T(N) � not fully correct ! 24

Theta Notation (θ) �Example : T(N) = 3 N 2 T(N) = O(N 4) T(N) = O(N 3) T(N) = θ(N 2) best 25

Little O Notation (o) �Definition : T(N) = o(p(N)) if T(N) = O(p(N)) and T(N)≠θ(p(N)) �f(N) grows strictly faster than T(N) �growth rate of T(N) is less than the growth rate of f(N) for large N �f(N) is an upperbound on T(N) (but not tight) � not fully correct ! 26

Little O Notation (o) �Example : T(N) = 3 N 2 T(N) = o(N 4) T(N) = o(N 3) T(N) = θ(N 2) 27

RULES �RULE 1: if T 1(N) = O(f(N)) and T 2(N) = O(g(N)) then a) T 1(N) + T 2(N) = max (O(f(N)), O(g(N))) b) T 1(N) * T 2(N) = O(f(N) * g(N)) You can prove these ? Is it true for θ notation ? What about Ω notation? 28

RULES �RULE 2: if T(N) is a polynomial of degree k T(N) = ak. Nk + ak-1 Nk-1 + … + a 1 N + a 0 then T(N) = θ(Nk) 29

RULES �RULE 3: logk N = o(N) for any constant k logarithm grows very slowly ! 30

Some Common Functions �c = o (log N) => c=O(log N) but c≠Ω(log. N) �log N = o(log 2 N) �log 2 N = o(N) �N = o(N log N) �N = o (N 2) �N 2 = o (N 3) �N 3 = o (2 N) 31

�Example : T(N) = 4 N 2 � T(N) = O(2 N 2) correct but bad style T(N) = O(N 2) drop the constants � T(N) = O(N 2+N) correct but bad style T(N) = O(N 2) ignore low order terms 32

Another Way to Compute Growth Rates 33

�Example : f(N) = 7 N 2 g(N) = N 2 + N 34

�Example : f(N) = N log. N g(N) = N 1. 5 compare log. N with N 0. 5 compare log 2 N with N compare log 2 N with o(N) N log. N = o(N 1. 5) 35