Data Structures and Algorithms Lecture 1 0 A

Data Structures and Algorithms Lecture 1 0 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Course objectives: n Assess how the choice of data structures and algorithm design methods impacts the performance of programs. n Choose the appropriate data structure and algorithm design method for a specified application. n Solve problems using data structures such as linear lists, stacks, queues, hash tables, …. n Solve problems using algorithm design methods such as the greedy method, divide and conquer. 1 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Agenda n Administrative n Course objective and outline 2 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Introduction n What is Algorithm? n a clearly specified set of simple instructions to be followed to solve a problem n Takes a set of values, as input and n produces a value, or set of values, as output n May be specified n In English n As a computer program n As a pseudo-code n Data structures n Methods of organizing data n Program = algorithms + data structures A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1 3

Objectives n Analysis of algorithms n The theoretical study of the computer-program performance and resource usage. n Design of algorithms n data structures techniques 4 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Expectation n Assumed Knowledge n Some experience in Java or other similar OO language n BEFORE each lecture n Download and printout the lecture slides n Read the related chapter (s) and lectures notes n Make sure you keep up with the progress n Consult course staff EARLY enough for difficulties and problems! 5 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Our Textbook n Anany Levitin, Introduction to The Design & Analysis of Algorithms, 2 rd edition. 6 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Rule of Conducts n n Okay to discuss ideas and problem approaches All work must be your own creation Turn off your mobile phone during the class Be on time 7 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Questions? 8 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

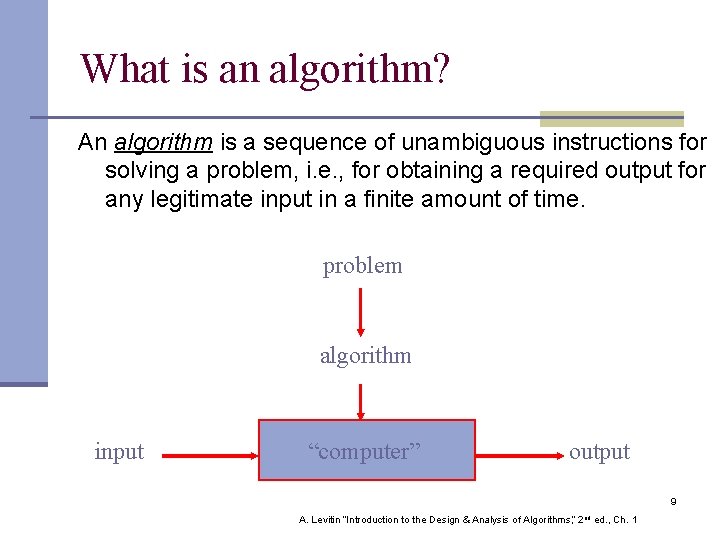
What is an algorithm? An algorithm is a sequence of unambiguous instructions for solving a problem, i. e. , for obtaining a required output for any legitimate input in a finite amount of time. problem algorithm input “computer” output 9 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Historical Perspective n Muhammad ibn Musa al-Khwarizmi – 9 th century mathematician www. lib. virginia. edu/science/parshall/khwariz. html 10 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example of computational problem: sorting n Statement of problem: n Input: A sequence of n numbers <a 1, a 2, …, an> n Output: A reordering of the input sequence <a´ 1, a´ 2, …, a´n> so that a´i ≤ a´j whenever i < j n Instance: The sequence <5, 3, 2, 8, 3> n Algorithms: n n Selection sort Insertion sort Merge sort (many others) 11 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Selection Sort n Input: array a[1], …, a[n] n Output: array a sorted in non-decreasing order n Algorithm: n for i=1 to n swap a[i] with smallest of a[i], …a[n] 12 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Analysis of Algorithms n How good is the algorithm? n Correctness n Time efficiency n Space efficiency n Does there exist a better algorithm? n Lower bounds n Optimality 13 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

What is an algorithm? n 1. 2. 3. 4. n Recipe, process, method, technique, procedure, routine, … with following requirements: Finiteness b terminates after a finite number of steps Definiteness b rigorously and unambiguously specified Input b valid inputs are clearly specified Output b can be proved to produce the correct output given a valid input Effectiveness 1. steps are sufficiently simple and basic 14 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Why study algorithms? n Theoretical importance n the core of computer science n Practical importance n A practitioner’s toolkit of known algorithms n Framework for designing and analyzing algorithms for new problems 15 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Analysis of algorithms n How good is the algorithm? n time efficiency n space efficiency n Does there exist a better algorithm? n lower bounds n optimality 16 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Important problem types n sorting n searching n string processing n graph problems n combinatorial problems n geometric problems n numerical problems 17 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Fundamental data structures n list n graph n array n tree n linked list n set and dictionary n string n stack n queue n priority queue 18 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Questions? 19 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Chapter Fundamentals of the Analysis of Algorithm Efficiency (1) 20 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Introduction n What is Algorithm? n a clearly specified set of simple instructions to be followed to solve a problem n Takes a set of values, as input and n produces a value, or set of values, as output n May be specified n In English n As a computer program n As a pseudo-code n Data structures n Methods of organizing data n Program = algorithms + data structures A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Introduction n Why need algorithm analysis ? n writing a working program is not good enough n The program may be inefficient! n If the program is run on a large data set, then the running time becomes an issue A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Algorithm Analysis… n Factors affecting the running time n computer n compiler n algorithm used n input to the algorithm n The content of the input affects the running time n typically, the input size (number of items in the input) is the main consideration § E. g. sorting problem the number of items to be sorted § E. g. multiply two matrices together the total number of elements in the two matrices n Machine model assumed n Instructions are executed one after another, with no concurrent operations Not parallel computers A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example n Calculate 1 1 2 2 N+2 3 4 N 4 1 n Lines 1 and 4 count for one unit each n Line 3: executed N times, each time four units n Line 2: (For… 1 for initialization, N+1 for all the tests, N for all the increments) total 2 N + 2 n total cost: 6 N + 4 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Selection Problem n Given a list of N numbers, determine the kth largest, where k N. n Algorithm 1: (1) Read N numbers into an array (2) Sort the array in decreasing order by some simple algorithm (3) Return the element in position k A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Selection Problem… n Algorithm 2: (1) Read the first k elements into an array and sort them in decreasing order (2) Each remaining element is read one by one n n If smaller than the kth element, then it is ignored Otherwise, it is placed in its correct spot in the array, bumping one element out of the array. (3) The element in the kth position is returned as the answer. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Selection Problem… n Which algorithm is better when n N =100 and k = 100? n N =100 and k = 1? n What happens when N = 1, 000 and k = 500, 000? n There exist better algorithms A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Theoretical analysis of time efficiency Time efficiency is analyzed by determining the number of repetitions of the basic operation as a function of input size Basic operation: the operation that contributes most towards the running time of the algorithm input size running time T(n) ≈ cop. C(n) Number of times basic operation is executed execution time for basic operation. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1 28

Best-case, average-case, worst-case For some algorithms efficiency depends on form of input: n Worst case: Cworst(n) – maximum over inputs of size n n Best case: Cbest(n) – minimum over inputs of size n n Average case: Cavg(n) – “average” over inputs of size n n Number of times the basic operation will be executed on typical input n NOT the average of worst and best case n Expected number of basic operations considered as a random variable under some assumption about the probability distribution of all possible inputs 29 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Input size and basic operation examples Problem Input size measure Basic operation Searching for key in a list of n items Number of list’s items, i. e. Key comparison n Multiplication of two matrices Matrix dimensions or total number of elements Multiplication of two numbers Checking primality of a n’size = number of digits Division given integer n (in binary representation) Typical graph problem #vertices and/or edges Visiting a vertex or traversing an edge 30 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Sequential search n Worst case n Best case n Average case 31 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Sequential search (Count. ) n Worst case The last number n 32 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Example: Sequential search (Count. ) n Worst case The last number n 33 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Binary Search n Used with a sorted list n First check the middle list element n If the target matches the middle element, we are done n If the target is less than the middle element, the key must be in the first half n If the target is larger than the middle element, the key must be in the second half A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Binary Search Example A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Binary Search Algorithm start = 1 end = N while start ≤ end do middle = (start + end) / 2 switch (Compare(list[middle], target)) case -1: case 0: case 1: start = middle + 1 break return middle break end = middle – 1 break end select end while return 0 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Algorithm Review n Each comparison eliminates about half of the elements of the list from consideration n If we begin with N = 2 k – 1 elements in the list, there will be 2 k– 1 elements on the second pass, and 2 k– 2 – 1 elements on the third pass A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Worst-Case Analysis n In the worst case, we will either find the target on the last pass, or not find the target at all n The last pass will have only one element left to compare, which happens when 21 -1 = 1 n If N = 2 k – 1, then there must be k = log(N+1) passes A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1

Questions? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 2 nd ed. , Ch. 1