Data Structures and Algorithms in Parallel Computing Lecture

Data Structures and Algorithms in Parallel Computing Lecture 2

Parallel algorithmic techniques • Techniques used in parallel algorithm design • Some are extensions of sequential algorithms’ design approaches • Others are specific to parallel algorithms • Methods: – Divide-and-conquer – Randomization – Parallel pointer manipulation

Divide-and-conquer • Split problem in subproblems – Easier to solve than original problem • Merge solutions to construct global solution • Improves program modularity • May lead to simple but efficient algorithms • Powerful tool in sequential algorithm design

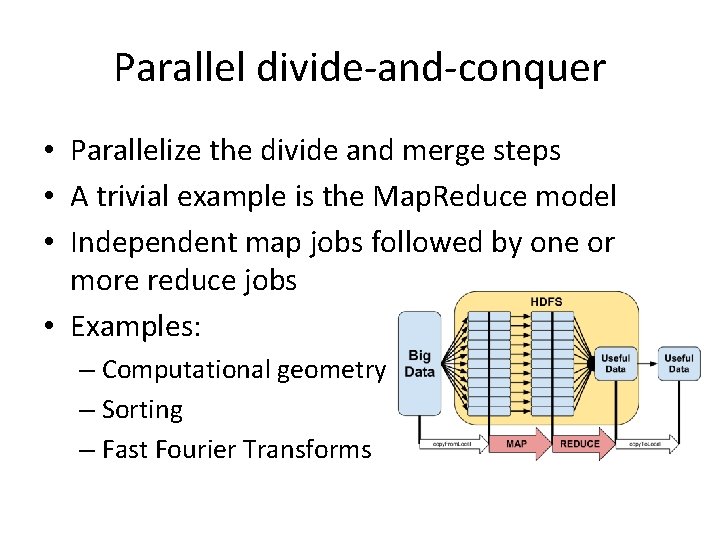
Parallel divide-and-conquer • Parallelize the divide and merge steps • A trivial example is the Map. Reduce model • Independent map jobs followed by one or more reduce jobs • Examples: – Computational geometry – Sorting – Fast Fourier Transforms

Example: mergesort • Takes a sequence of n keys and returns the ordered list • Split sequence in two sequences of n/2 keys • Recursively sort the two sequences • Merge the two sorted n/2 keys sequence • O(n) time complexity • Runtime

Parallel mergesort • Recursive calls are independent

Complexity analysis • Hence the complexity is W(n)/D(n) = O(n log n)/O(n) = O(log n) • Merge phase is sequential bottleneck – Need to improve the depth of the merge phase

Improvements • Parallel merge C. P. Kruskal. Searching, merging, and sorting in parallel computation. IEEE Trans. Comput. , C– 32(10): 942– 946, Oct. 1983 • Pipelined divide-and-conquer : O(log n) – Start the merge phase at the top level before the recursive calls complete R. Cole. Parallel merge sort. SIAM Journal of Computing, 17(4): 770– 785, Aug. 1988

Randomization • Random numbers used in parallel algorithms to ensure that processors make local decisions which with high probability add up to global decisions • Techniques – Sampling – Symmetric breaking – Load balancing

Sampling • Select a representative sample from a set of elements • Solve the problem on that sample • Use the solution to guide the solution for the original set • Example: sorting

Number sorting • Partition the keys into non-overlapping intervals and sort each interval • Each interval must contain approximatively the same number of keys • Random sampling used to determine the interval boundaries – Select a random sample of keys – All selected keys are sorted together – Sorted keys are used as boundaries • Examples: computational geometry, graphs, string matching

Symmetry breaking • Phenomenon in which small fluctuations acting on a system crossing a critical point decide the system’s fate • Example: – Select a large number of independent graph vertices in parallel – Vertices are not neighbors • If one vertex joins the set all of its neighbors must deny to join – Difficult if the structure of each vertex is the same – Randomness is used to break the symmetry between vertices

Load balancing • Evenly distribute a large number of items across processors • Randomly assign each element to a subset • Good results if the average size of a subset is at least logarithmic in the size of the original set

Parallel pointer techniques • Sequential techniques for manipulating lists, trees, graphs, do not translate easily into parallel techniques • Examples: – Traversing the elements of a linked list – Visiting the list of nodes in postorder – Performing a depth first search • Solution: replace them with equivalent parallel techniques

Pointer jumping • In each step, each node in parallel replaces its pointer with that of its successor (or parent for trees) • Example – Label each node of an n-node list with the label of the last node (or root) – Log n steps for each node to point to the same node

Euler tour • A path through the graph in which every edge is traversed exactly once • Example – Euler tour of an undirected tree is computed by following the perimeter of the tree visiting each edge twice (on the way down and then up) • Keeping the Euler tour it is possible to compute many functions on the tree • O(n) - independent on the depth of the tree

Graph contraction • Reduce size of a graph while keeping some of its original structure • Example – Graph partitioning • Collapse high density vertices recursively • Find connected components • Expand the connected components to original graph

Ear decomposition • Partition a graph into an ordered collection of paths – – First path is a cycle The rest are called ears End-points of each ear are anchored on previous paths Can be used to determine of 2 edges are on a common cycle • Example – Determining biconnectivity, triconnectivity, 4 -connectivity, planarity, replace depth first search • Logarithmic depth and linear work

What’s next? • Graph parallel algorithms • BSP model – SSSP, connected components, pagerank • Vertex centric vs. subgraph centric • Load balancing – Importance of partitioning and graph type • . . .