Data Structures and Algorithms CSCE 221 Dr Scott

Data Structures and Algorithms CSCE 221 Dr. Scott Schaefer 1

Staff n n n Instructor u Dr. Scott Schaefer u HRBB 527 B u Office Hours: MTWR 9: 30 am – 10 am, F 9 am-10 am (or by appointment) TA u Zain Shamsi u HRBB 501 C u Office Hours: TR noon-2 pm Peer Teacher u Colton Williams u RDMC 111 B u Office Hours: MW noon-1 pm, F noon-2 pm 2/36

What will you learn? n n n n n Analysis of Algorithms Stacks, Queues, Deques Vectors, Lists, and Sequences Trees Priority Queues & Heaps Maps, Dictionaries, Hashing Skip Lists Binary Search Trees Sorting and Selection Graphs 3/36

Prerequisites n CSCE 121 “Introduction to Program Design and Concepts” or (ENGR 112 “Foundations of Engineering” and CSCE 113 “Intermediate Programming & Design”) n CSCE 222 “Discrete Structures” or MATH 302 “Discrete Mathematics” (either may be taken concurrently with CSCE 221) 4/36

Textbook 5/36

More on Assignments Turn in code/homeworks via CSNET (get an account if you don’t already have one) n Due by 11: 59 pm on day specified n All programming in C++ n Code, proj file, sln file, and Win 32 executable n Make your code readable (comment) n You may discuss concepts, but coding is individual (no “team coding” or web) n 6/36

Grading 3% Labs n 12% Homework n 35% Programming Assignments n 10% Quizzes n 20% Midterm n 20% Final n 7/36

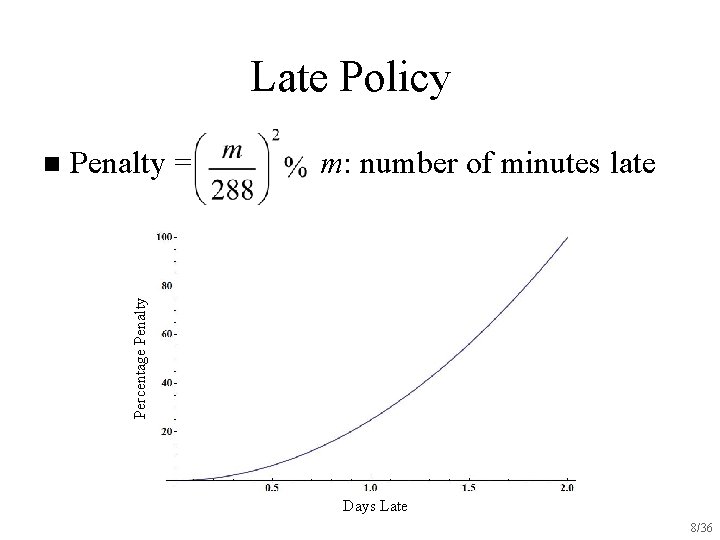
Late Policy Penalty = m: number of minutes late Percentage Penalty n Days Late 8/36

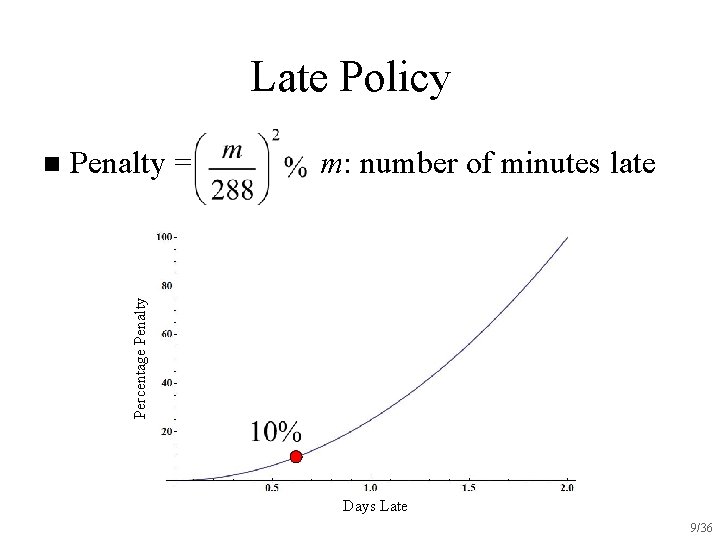
Late Policy Penalty = m: number of minutes late Percentage Penalty n Days Late 9/36

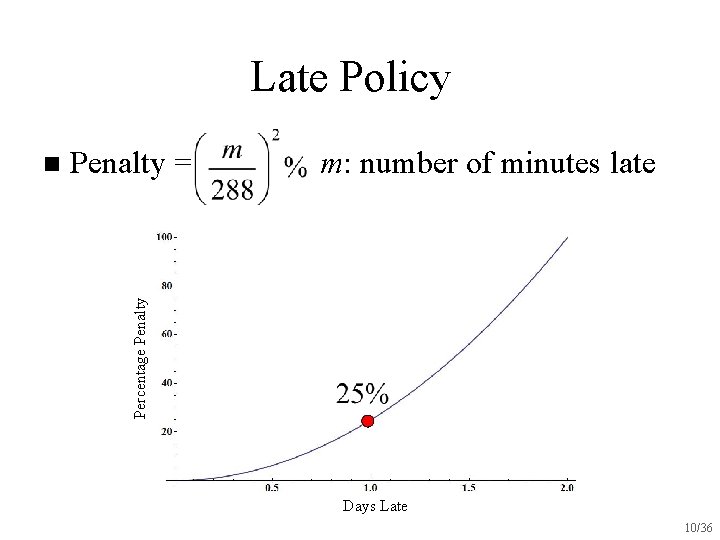
Late Policy Penalty = m: number of minutes late Percentage Penalty n Days Late 10/36

Labs n Several structured labs at the beginning of class with (simple) exercises u Graded on completion u Time to work on homework/projects 11/36

Homework Between 5 -10 n Written/Typed responses n Simple coding if any n 12/36

Programming Assignments 5 throughout the semester n Implementation of data structures or algorithms we discusses in class n Written portion of the assignment n 13/36

Quizzes Approximately 10 throughout the semester n Short answer, small number of questions n Will only be given in class or lab u Must be present to take the quiz n 14/36

Academic Honesty Assignments are to be done on your own u May discuss concepts, get help with a persistent bug u Should not copy work, download code, or work together with other students unless specifically stated otherwise n We use a software similarity checker n 15/36

Class Discussion Board n piazza. com/tamu/summer 2013/csce 221100 n Sign up as a student 16/36

Asymptotic Analysis 17/36

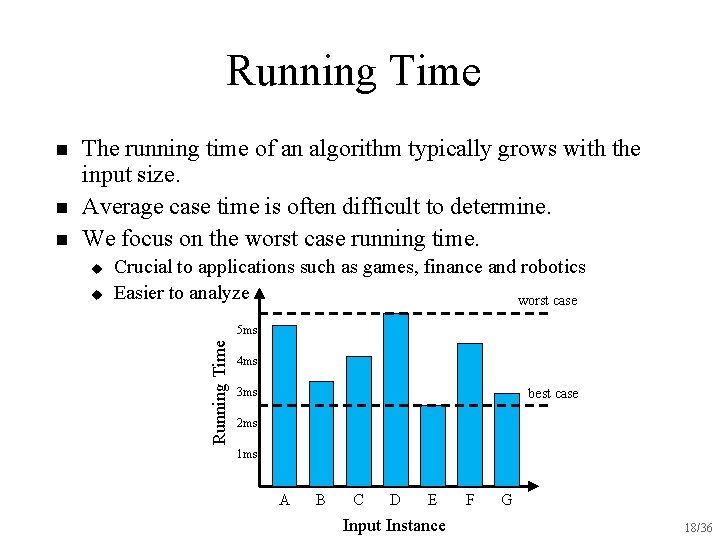
Running Time n n The running time of an algorithm typically grows with the input size. Average case time is often difficult to determine. We focus on the worst case running time. u u Crucial to applications such as games, finance and robotics Easier to analyze worst case 5 ms Running Time n 4 ms 3 ms best case 2 ms 1 ms A B C D E Input Instance F G 18/36

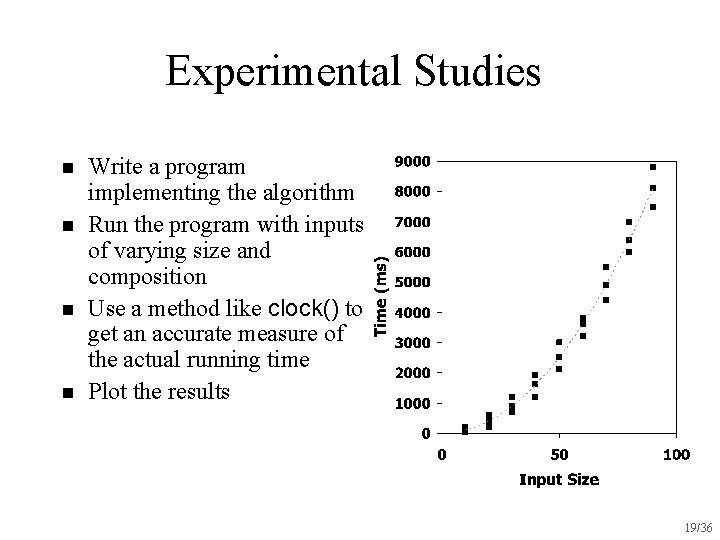
Experimental Studies n n Write a program implementing the algorithm Run the program with inputs of varying size and composition Use a method like clock() to get an accurate measure of the actual running time Plot the results 19/36

Stop Watch Example 20/36

Limitations of Experiments It is necessary to implement the algorithm, which may be difficult n Results may not be indicative of the running time on other inputs not included in the experiment. n In order to compare two algorithms, the same hardware and software environments must be used n 21/36

Theoretical Analysis Uses a high-level description of the algorithm instead of an implementation n Characterizes running time as a function of the input size, n. n Takes into account all possible inputs n Allows us to evaluate the speed of an algorithm independent of the hardware/software environment n 22/36

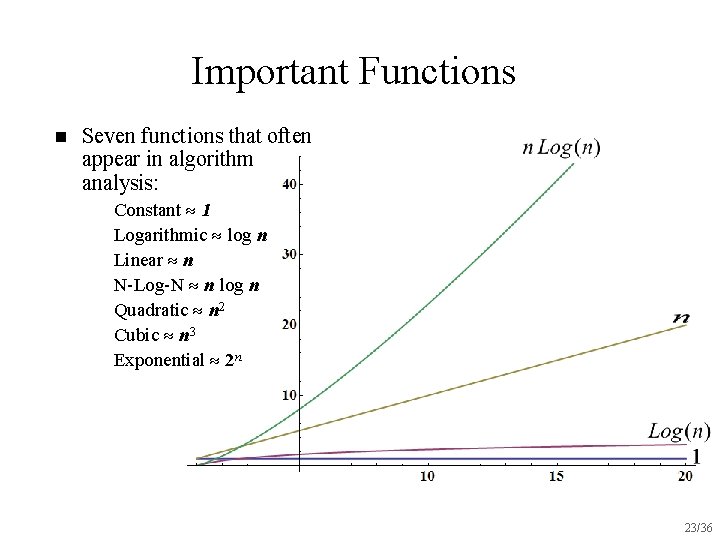
Important Functions n Seven functions that often appear in algorithm analysis: u u u u Constant 1 Logarithmic log n Linear n N-Log-N n log n Quadratic n 2 Cubic n 3 Exponential 2 n 23/36

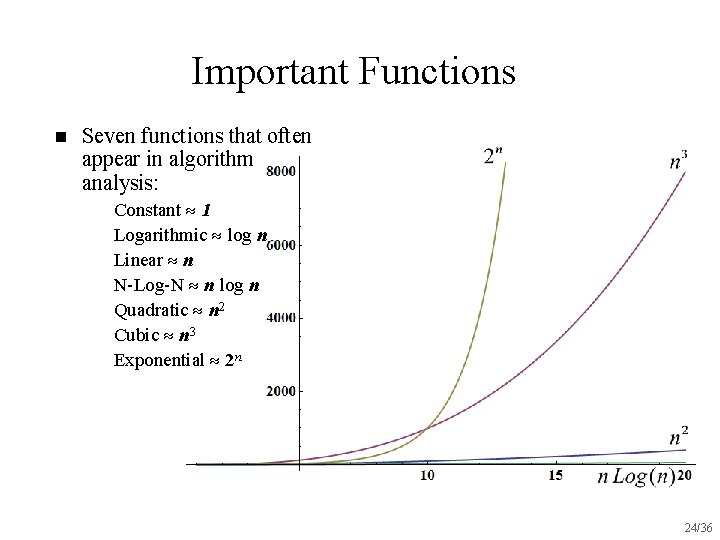
Important Functions n Seven functions that often appear in algorithm analysis: u u u u Constant 1 Logarithmic log n Linear n N-Log-N n log n Quadratic n 2 Cubic n 3 Exponential 2 n 24/36

Why Growth Rate Matters if runtime is. . . time for n + 1 time for 2 n time for 4 n c lg (n + 1) c (lg n + 1) c(lg n + 2) cn c (n + 1) 2 c n 4 c n lg n ~ c n lg n + cn 2 c n lg n + 2 cn 4 c n lg n + 4 cn c n 2 ~ c n 2 + 2 c n 4 c n 2 16 c n 2 c n 3 ~ c n 3 + 3 c n 2 8 c n 3 64 c n 3 c 2 n c 2 n+1 c 2 2 n c 2 4 n runtime quadruples when problem size doubles 25/36

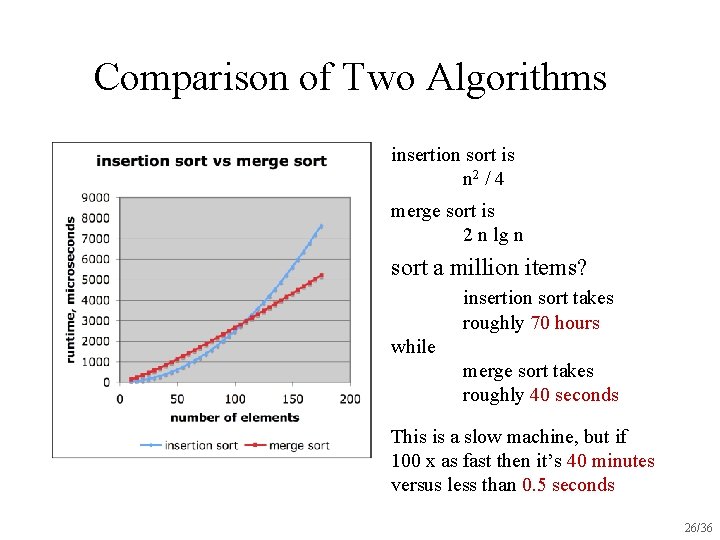
Comparison of Two Algorithms insertion sort is n 2 / 4 merge sort is 2 n lg n sort a million items? insertion sort takes roughly 70 hours while merge sort takes roughly 40 seconds This is a slow machine, but if 100 x as fast then it’s 40 minutes versus less than 0. 5 seconds 26/36

Constant Factors n The growth rate is not affected by u u n constant factors or lower-order terms Examples u u 102 n + 105 is a linear function 105 n 2 + 108 n is a quadratic function 27/36

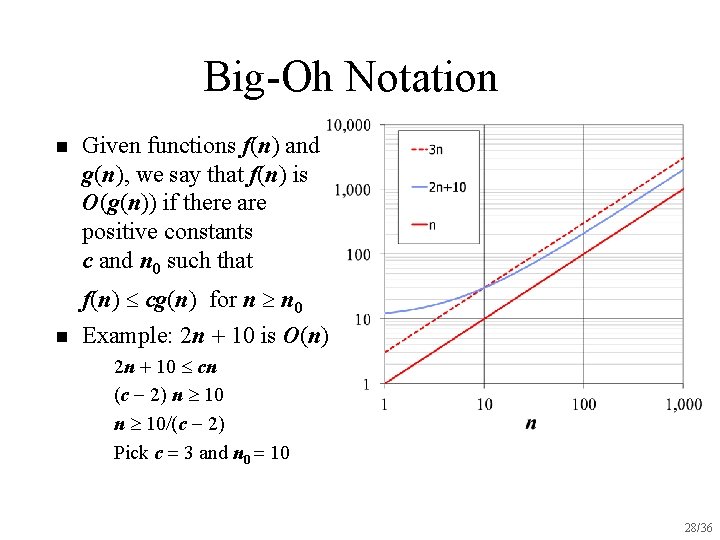
Big-Oh Notation n n Given functions f(n) and g(n), we say that f(n) is O(g(n)) if there are positive constants c and n 0 such that f(n) cg(n) for n n 0 Example: 2 n + 10 is O(n) u u 2 n + 10 cn (c 2) n 10/(c 2) Pick c = 3 and n 0 = 10 28/36

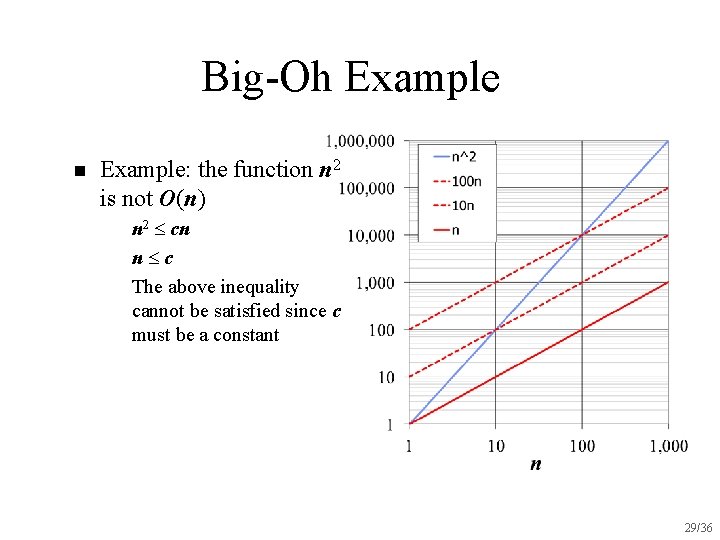
Big-Oh Example n Example: the function n 2 is not O(n) u u u n 2 cn n c The above inequality cannot be satisfied since c must be a constant 29/36

More Big-Oh Examples 7 n-2 is O(n) need c > 0 and n 0 1 such that 7 n-2 c • n for n n 0 this is true for c = 7 and n 0 = 1 n 3 n 3 + 20 n 2 + 5 is O(n 3) need c > 0 and n 0 1 such that 3 n 3 + 20 n 2 + 5 c • n 3 for n n 0 this is true for c = 4 and n 0 = 21 n 3 log n + 5 is O(log n) need c > 0 and n 0 1 such that 3 log n + 5 c • log n for n n 0 this is true for c = 8 and n 0 = 2 30/36

Big-Oh and Growth Rate n n n The big-Oh notation gives an upper bound on the growth rate of a function The statement “f(n) is O(g(n))” means that the growth rate of f(n) is no more than the growth rate of g(n) We can use the big-Oh notation to rank functions according to their growth rate g(n) grows more f(n) grows more Same growth f(n) is O(g(n)) g(n) is O(f(n)) Yes No Yes 31/36

Big-Oh Rules n If is f(n) a polynomial of degree d, then f(n) is O(nd), i. e. , 1. 2. n Use the smallest possible class of functions u n Drop lower-order terms Drop constant factors Say “ 2 n is O(n)” instead of “ 2 n is O(n 2)” Use the simplest expression of the class u Say “ 3 n + 5 is O(n)” instead of “ 3 n + 5 is O(3 n)” 32/36

Computing Prefix Averages n n We further illustrate asymptotic analysis with two algorithms for prefix averages The i-th prefix average of an array X is average of the first (i + 1) elements of X: A[i] = (X[0] + X[1] + … + X[i])/(i+1) 33/36

Prefix Averages (Quadratic) The following algorithm computes prefix averages in quadratic time by applying the definition Algorithm prefix. Averages 1(X, n) Input array X of n integers Output array A of prefix averages of X #operations A new array of n integers n for i 0 to n 1 do n s X[0] n for j 1 to i do 1 + 2 + …+ (n 1) s s + X[j] 1 + 2 + …+ (n 1) A[i] s / (i + 1) n return A 1 34/36

Arithmetic Progression n The running time of prefix. Averages 1 is O(1 + 2 + …+ n) The sum of the first n integers is n(n + 1) / 2 Thus, algorithm prefix. Averages 1 runs in O(n 2) time 35/36

Prefix Averages (Linear) The following algorithm computes prefix averages in linear time by keeping a running sum Algorithm prefix. Averages 2(X, n) Input array X of n integers Output array A of prefix averages of X A new array of n integers s 0 for i 0 to n 1 do s s + X[i] A[i] s / (i + 1) return A #operations n 1 n n n 1 Algorithm prefix. Averages 2 runs in O(n) time 36/36