Data Structures and Algorithms Analysis of Algorithms Richard

Data Structures and Algorithms Analysis of Algorithms Richard Newman

Players Boss/Manager/Customer – Wants a cheap solution – Cheap = efficient Programmer/developer – Wants to solve the problem, deliver system Theoretician – Wants to understand Student – Might play any or all of these roles some day

Why Analyze Algorithms? • • Predict performance Compare algorithms Provide guarantees Understand theory • Practical reason: avoid poor performance! • Also – avoid logical/design errors

Algorithmic Success Stories • DFT Discrete Fourier Transform Take N samples of waveform Decompose into periodic components • Used in DVD, JPEG, MRI, astrophysics, . . • Brute force: N 2 steps • FFT algorithm: N lg N steps

Algorithmic Success Stories • B-Body Simulation Simulate gravitational interactions among N bodies • Brute force: N 2 steps • Barnes-Hut algorithm: N lg N steps

The Challenge Will my algorithm be able to solve problem with large practical input? – Time – Memory – Power Knuth (1970's) – use scientific method to understand performance

Scientific Method Observe feature of natural world Hypothesize a model consistent with observations Predict events using hypothesis Test predictions experimentally Iterate until hypothesis and observations agree

Scientific Method Principles Experiments must be reproducible Hypotheses must be falsifiable

Example: 3 -Sum Given N distinct integers, how many triples sum up to exactly zero % cat 8 ints. txt 8 30 -40 -20 -10 40 0 10 5 %. /Three. Sum 8 ints. txt 4

3 -Sum Brute Force Algo For i=0 to N-1 For j=i+1 to N-1 For k=j+1 to N-1 If a[i] + a[j] + a[k] == 0 count++ return count

Measuring Running Time Manually Start stopwatch when starting program Stop it when program finishes Can do this in script (date) Internally Use C library function time() Can insert calls around code of interest – Avoid initialization, etc.

Measuring Running Time Strategy Run program on various input sizes Measure time for each Can do this in script also Plot results tools: http: //www. opensourcetesting. org/performance. php

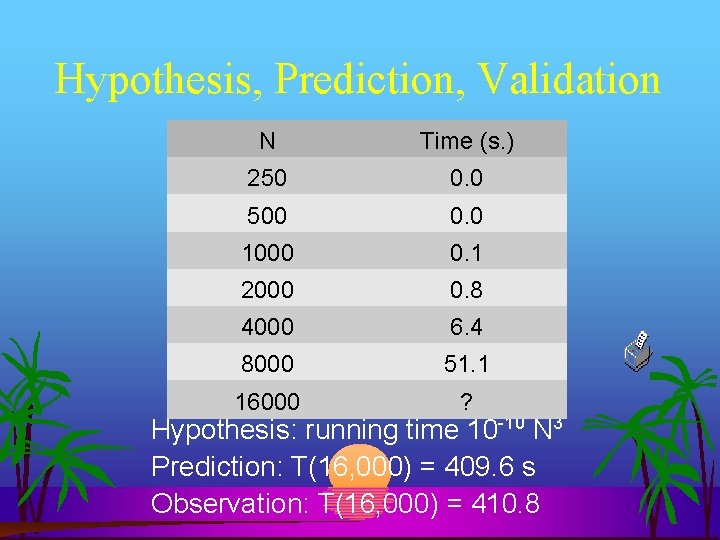
Measuring Running Time N Time (s. ) 250 0. 0 500 0. 0 1000 0. 1 2000 0. 8 4000 6. 4 8000 51. 1 16000 ? What do you think the time will be for input of size 16, 000? Why?

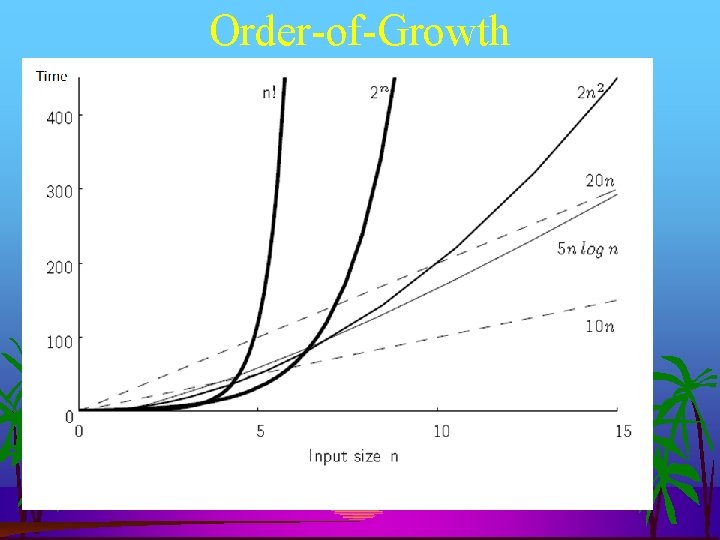
Data Analysis Standard Plot running time T(N) vs. input size N Use linear scales for both

Data Analysis Log-log Plot If straight line Slope gives power lg y = m lg x + b y = 2 b xm

Hypothesis, Prediction, Validation N Time (s. ) 250 0. 0 500 0. 0 1000 0. 1 2000 0. 8 4000 6. 4 8000 51. 1 16000 ? Hypothesis: running time 10 -10 N 3 Prediction: T(16, 000) = 409. 6 s Observation: T(16, 000) = 410. 8

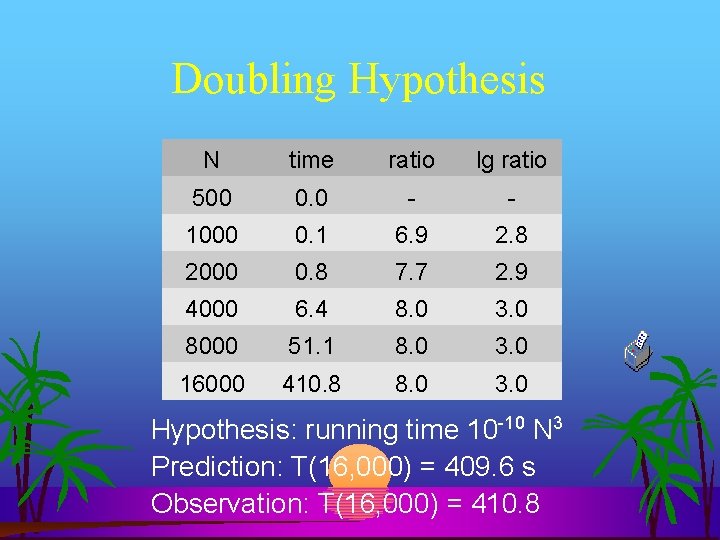
Doubling Hypothesis Quick way to estimate slope m in log-log plot Strategy: Double size of input each run Run program on doubled input sizes Measure time for each Take ratio of times If polynomial, should converge to power

Doubling Hypothesis N time ratio lg ratio 500 0. 0 - - 1000 0. 1 6. 9 2. 8 2000 0. 8 7. 7 2. 9 4000 6. 4 8. 0 3. 0 8000 51. 1 8. 0 3. 0 16000 410. 8 8. 0 3. 0 Hypothesis: running time 10 -10 N 3 Prediction: T(16, 000) = 409. 6 s Observation: T(16, 000) = 410. 8

Doubling Hypothesis: running time is about a. Nb With b = lg(ratio of running times) Caveat!!! Cannot identify logarithmic factors How to find a? Take large input, equate time to hypothesized time with b as estimated, then solve for a

Experimental Algorithmics System Independent Effects Algorithm Input data

Experimental Algorithmics System Dependent Effects Hardware: CPU, memory, cache, . . . Software: compiler, interpreter, garbage collection, . . . System: OS, network, other processes

Experimental Algorithmics Bad news Hard to get precise measurements Good news Easier than other physical sciences! Can run huge number of experiments

Mathematical Running Time Models Total running time = sum (cost x freq) Need to analyze program to determine set of operations over which weighted sum is computed Cost depends on machine, compiler Frequency depends on algorithm, input data Donald Knuth 1974 Turing Award

How to Estimate Constants? Operation example Time* (ns) Integer add a+b 2. 1 Integer multiply a*b 2. 4 Integer divide a/b 5. 4 Fp add a+b 4. 6 Fp multiply a*b 4. 2 Fp divide a/b 13. 5 sine Math. sine(theta) 91. 3 arctangent Math. atan 2(x, y) 129. 0 . . *Running OS X on Macbook Pro 2. 2 GHz 2 GB RAM

Experimental Algorithmics Observation: most primitive functions take constant time Warning: non-primitive often do not! How many instructions as f(input size)? int count = 0; for (int i = 1; i < N; ++i) if (a[i] == 0) count++;

Experimental Algorithmics int count = 0; for (int i = 1; i < N; ++i) if (a[i] == 0) count++; Operation Frequency Var declaration 2 assignment 2 < compare N+1 == compare N array access N increment N to 2 N

Counting Frequency - Loops int count = 0; for (int i = 1; i < N; ++i) for (int j = i+1; j < N, ++j) if (a[i] + a[j] == 0) count++; How many additions in loop? N-1 + N-2 +. . . + 3 + 2 + 1 = (1/2) N (N-1) Exact number of other operations? Tedious and difficult. .

Experimental Algorithmics Observation: tedious at best Still may have noise! Approach: Simplify! Use some basic operation as proxy e. g. , array accesses int count = 0; for (int i = 1; i < N; ++i) for (int j = i+1; j < N; ++j) if (a[i] + a[j] == 0) count++;

Experimental Algorithmics Observation: lower order terms become less important as input size increases Still may be important for “small” inputs Approach: Simplify! Use ~ Ignore lower order terms – N large, they are negligible – N small, who cares?

Leading Term Approximation Examples Ex 1: 1/6 N 3 + 20 N + 16 ~ 1/6 N 3 Ex 2: 1/6 N 3 + 100 N 4/3 + 56 ~ 1/6 N 3 Ex 3: 1/6 N 3 – 1/2 N 2 + 1/3 N ~ 1/6 N 3 Discard lower order terms e. g. , N=1000, 166. 67 million vs. 166. 17 million

Leading Term Approximation Technical definition: f(N) ~ g(N) means limit =1 N -> inf g(N)

Bottom Line int count = 0; for (int i = 1; i < N; ++i) for (int j = i+1; j < N, ++j) if (a[i] + a[j] == 0) count++; How many array accesses in loop? ~ N 2 Use cost model and ~ notation!

Example - 3 -Sum int count = 0; for (int i = 1; i < N; ++i) for (int j = i+1; j < N; ++j) for (int k = j+1; k < N; ++k) if (a[i] + a[j] + a[k] == 0) count++; How many array accesses in loop? Execute N (N-1)(N-2)/3! Times ~ (1/6)N 3 ~ (1/2) N 3 array accesses (3 per stmt) Use cost model and ~ notation!

Estimating Discrete Sums Take Discrete Math (remember? ) Telescope series, inductive proof Approximate with integral Doesn't always work! Use Maple or Wolfram Alpha

Takeaway In principle, accurate mathematical models In practice Formulas can be complicated Advanced math might be needed Are subject to noise anyway Exact models – leave to experts! We will use approximate models

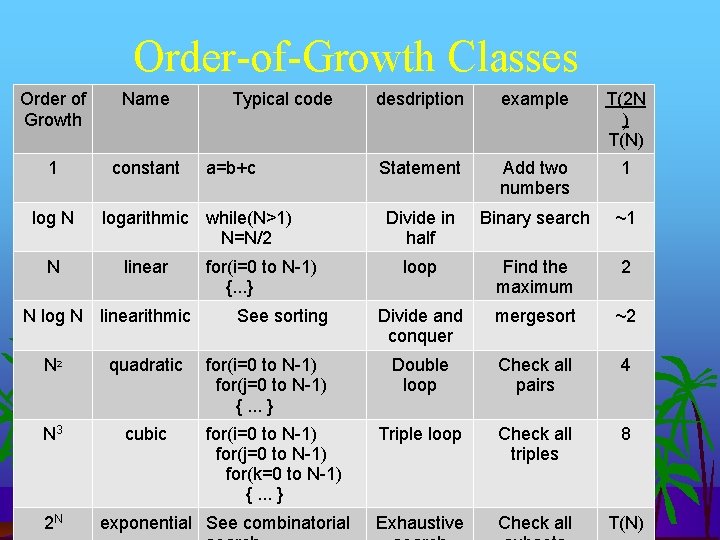
Order-of-Growth Classes Order of Growth Name 1 constant log N N a=b+c logarithmic while(N>1) N=N/2 linear N log N linearithmic N 2 quadratic N 3 cubic 2 N Typical code for(i=0 to N-1) {. . . } See sorting for(i=0 to N-1) for(j=0 to N-1) {. . . } for(i=0 to N-1) for(j=0 to N-1) for(k=0 to N-1) {. . . } exponential See combinatorial desdription example T(2 N ) T(N) Statement Add two numbers 1 Divide in half Binary search ~1 loop Find the maximum 2 Divide and conquer mergesort ~2 Double loop Check all pairs 4 Triple loop Check all triples 8 Exhaustive Check all T(N)

Order-of-Growth Definition: If f(N) ~ c g(N) for some constant c > 0, then f(N) is O(g(N)) – Ignores leading coefficient – Ignores lower order terms Brassard notation: O(g(N)) is the set of all functions with the same order So 3 -Sum algorithm is order N 3 – Leading coefficient depends on hardware, compiler, etc.

Order-of-Growth Good News! The following set of functions suffices to describe order of growth of most algorithms: 1, log N, N, N log N, N 2, N 3, 2 N, N!

Order-of-Growth

Binary Search Goal: Given a sorted array and a key, find the index of the key in the array Binary Search: Compare key against middle entry (of what is left) – Too small, go left – Too big, go right – Equal, found

Binary Search Implementation Trivial to implement? First binary search published in 1946 First bug-free version in 1962 Bug in Java's Arrays. binary. Search() discovered in 2006! http: //googleresearch. blogspot. com/2006/06/ extra-read-all-about-it-nearly. html

Binary Search – Math Analysis Proposition: BS uses at most 1+lg N key compares for a sorted array of size N Defn: T(N) = # key compares on sorted array of size <= N Recurrence: for N > 1, T(N) <= T(N/2) + 1 for N = 1, T(1) = 1

Binary Search – Math Analysis Recurrence: for N > 1, T(N) <= T(N/2) + 1 for N = 1, T(1) = 1 Pf Sketch: (Assume N a power of 2) T(N) <= T(N/2) + 1 <= T(N/4) + 1 <= T(N/8) + 1 + 1. . . <= T(N/N) + 1 + 1 +. . . + 1 = 1 + lg N

3 -Sum Version 0: N 3 time, N space Version 1: N 2 log N time, N space Version 2: N 2 time, N space

3 -Sum – 2 N log N Algorithm – Sort the N (distinct) integers – For each pair of numbers a[i] and a[j], – Binary Search for -(a[i] + a[j]) Analysis: Order of growth is N 2 log N – Step 1: N 2 using insertion sort – Step 2: N 2 log N with binary search Can achieve N 2 by modifying BS step

Comparing Programs Hypothesis: Version 1 is significantly faster in practice than Version 0 Version 1 N Time (s) 1000 0. 14 2000 0. 8 2000 0. 18 4000 6. 4 4000 0. 34 8000 51. 1 8000 0. 96 16000 3. 67 32000 14. 88 64000 59. 16 Theory works well in practice!

Memory Bit: 0 or 1 (binary digit) Byte: 8 bits (wasn't always that way) Megabyte (MB): 1 million or 220 bytes Gigabyte (GB): 1 billion or 230 bytes NIST and networks guys Everybody else

Memory 64 -bit machine: assume 8 -byte pointers • Can address more memory • Pointers use more space • Some JVMs “compress” ordinary object pointers to 4 bytes to avoid this cost

Typical Memory Usage Type Bytes boolean 1 char[ ] 2 N + 24 byte 1 int[ ] 4 N + 24 char 2 double[ ] 8 N + 24 int 4 float 4 long 8 Type Bytes double 8 char[ ][ ] ~2 MN int[ ][ ] ~4 MN double[ ][ ] ~8 MN Primitive types 1 -D arrays 2 -D arrays

Typical Java Memory Usage Object Overhead: 16 bytes Object Reference: 8 bytes Padding: Objects use multiple of 8 bytes Ex: Date object Object public class Date { Overhead private int day; day private int month; month year private int year; padding. . . } 16 bytes (OH) 4 bytes (int) 4 bytes (pad) 32 bytes total

Summary Empirical Analysis: Execute pgm to perform experiments Assume power law, formulate hypothesis for running time Model allows us to make predictions

Summary Mathematical Analysis: Analyze algo to count freq of operations Use tilde notation to simplify analysis Model allows us to explain behavior

Summary Scientific Method Mathematical model is independent of particular system, applies to machines not yet built Empirical approach needed to validate theory, and to make predictions

Next – Lecture 5 Read Chapter 3 Basic data structures