Data Structures Amihood Amir INPUT OUTPUT INPUT OUTPUT

Data Structures Amihood Amir

המחשב INPUT מדעי OUTPUT

המחשב INPUT מדעי OUTPUT

What Does Data Structures Mean? EXAMPLE: Input: Text T=T[1], … , T[n] of words. Query: Find occurrences of word P. Time: O(n|P|).

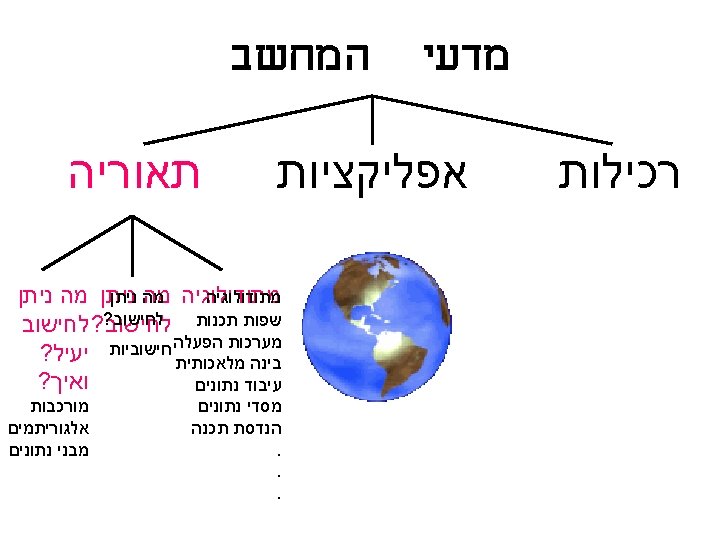
Can we do better? Concordance (index) : Construct a table C of pairs: <word, index> Sort the table lexicographically by word.

EXAMPLE: Let T= boa, aba, xavier, abracadabra, wonderful C= <aba, 2> <abracadabra, 4> <boa, 1> <wonderful, 5> <xavier, 3> Do binary search on C: Time: O((log n)|P|).

What Happened? We constructed an external structure (in the example, a table) That enabled answering our question faster. In this course we will see some basic such structures and the type of problems they enable to solve more efficiently.

Another Example Let’s play a game: Players: Two people. Input: A pile of gogoim. Moves: Take gogoim out of the pile. First player takes out 1 or 2 gogoim. Then alternately, can not exceed the number already taken out. Winner: The player who takes out the last gogoim.

Example pile 1 3 1 7 33 32 31 30 27 26 25 17 10 0 Total taken 1 1 2 3 6 7 8 16 23 1 1 8 10 I WIN !!!!

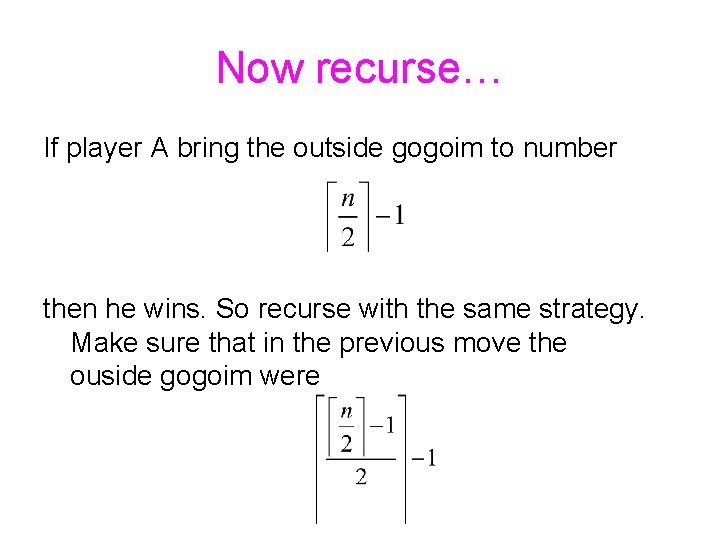
What is the strategy? Note that if there are n elements in the pile, and player A manages to bring the gogoim taken out of the pile to the number Then player B still can not win, but no matter what B does, he will bring the number of gogoim to more than half so A will then be able to win in the next move.

Now recurse… If player A bring the outside gogoim to number then he wins. So recurse with the same strategy. Make sure that in the previous move the ouside gogoim were

The LIFO The data structure we need is the LIFO – Last In First Out – Or stack ( )מחסנית.

Using the LIFO Let L be a stack, V a variable. Basic Operations: Push(L, V) -- pushes V into stack L. Pop(L, V) -- pops the top value out of stack L and puts it in variable V

A Winning Algorithm for our Game Our data structures: V = the current number of gogoim outside. L = the stack of “winning” number of gogoim outside. Initialization: V L empty.

A Winning Algorithm (2) Find winning sizes: While V > 2 do: PUSH(L, V) V End While You start. If V=2 take 2 gogoim. If V=1 take 1.

A Winning Algorithm (3) The Game: Variables: S = number of gogoim taken out so far. Initialize: S 0. The Game moves: While pile not empty do: POP(L, V) If this is first pop then take out V gogoim. S V else take out V-S gogoim. S V. Opponent makes his move. End While

A Sample Run n = 440/2 219/2 109/2 54/2 26/2 12/2 5/2 - 1 = 219 1 = 109 1 = 54 1 = 26 1 = 12 1=5 1=2

Stack Implementation Option 1: Array S[1], …, S[n]. First element in S[1]. Pointer top points to last element. Advantages: Simple. Disadvantages: Need to keep a long array for stack. When it fills, need to copy everything to a longer array.

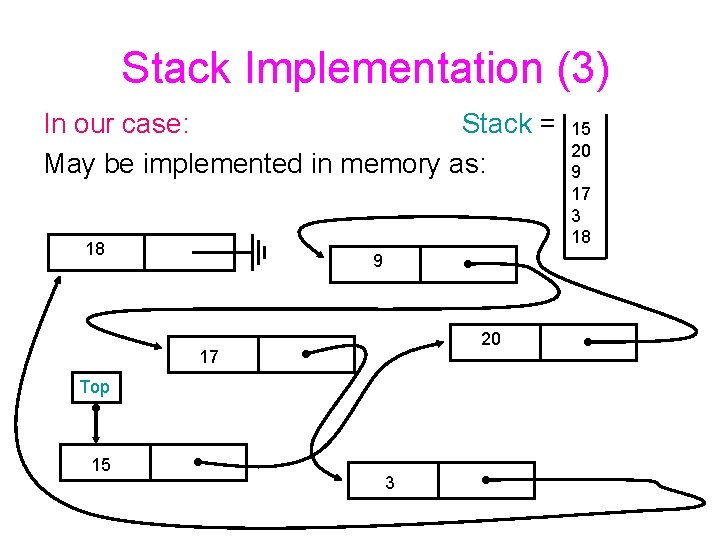
Stack Implementation (2) Option 2: Linked list of records. A record has a number of data fields and a pointer to the next record.

Stack Implementation (3) In our case: Stack = May be implemented in memory as: 18 9 20 17 Top 15 3 15 20 9 17 3 18

Stack Implementation (4) Advantages: Efficient for dynamic allocation of records. Disadvantages: More complicated to maintain.

Linked List Top

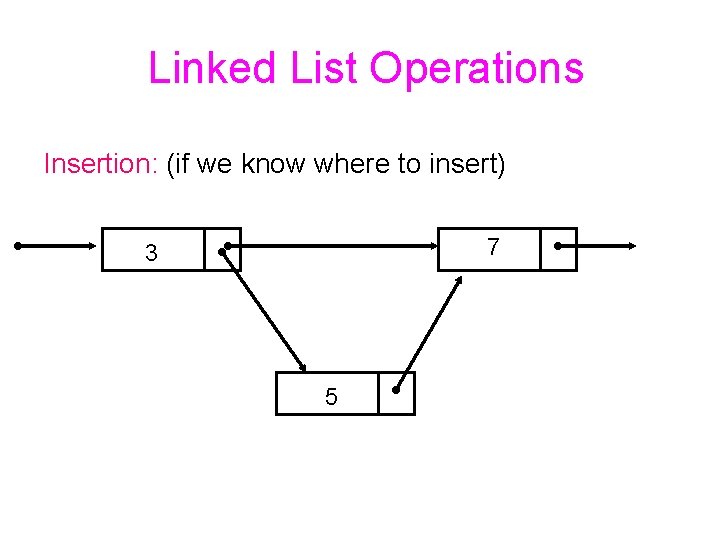
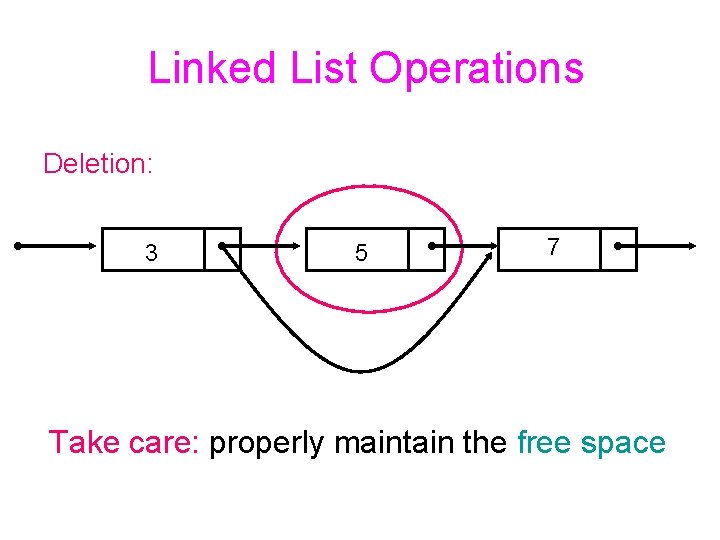
Linked List Operations Insertion: (if we know where to insert) 7 3 5

Linked List Operations Deletion: 3 5 7 Take care: properly maintain the free space

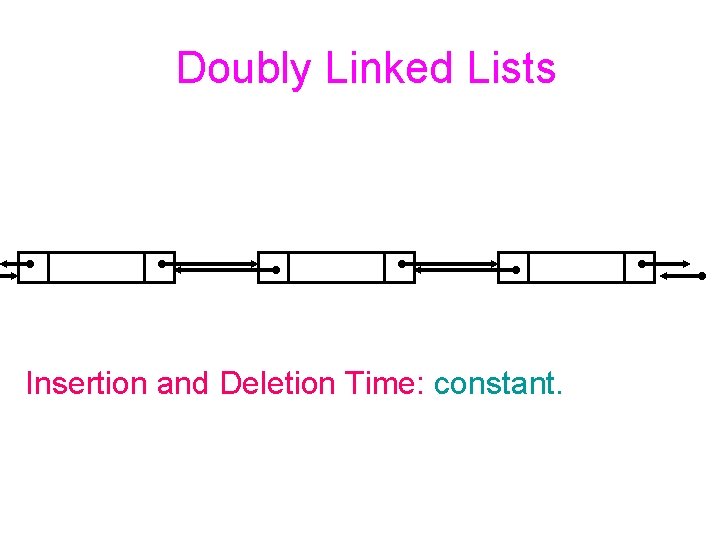
Doubly Linked Lists Insertion and Deletion Time: constant.

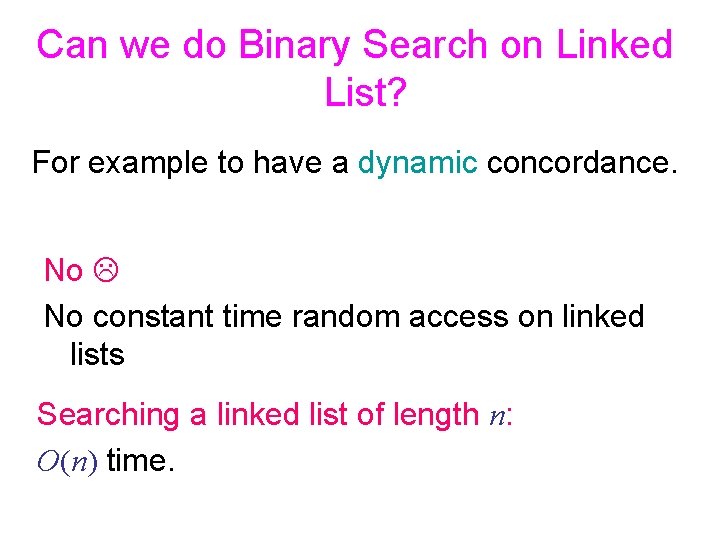
Can we do Binary Search on Linked List? For example to have a dynamic concordance. No constant time random access on linked lists Searching a linked list of length n: O(n) time.

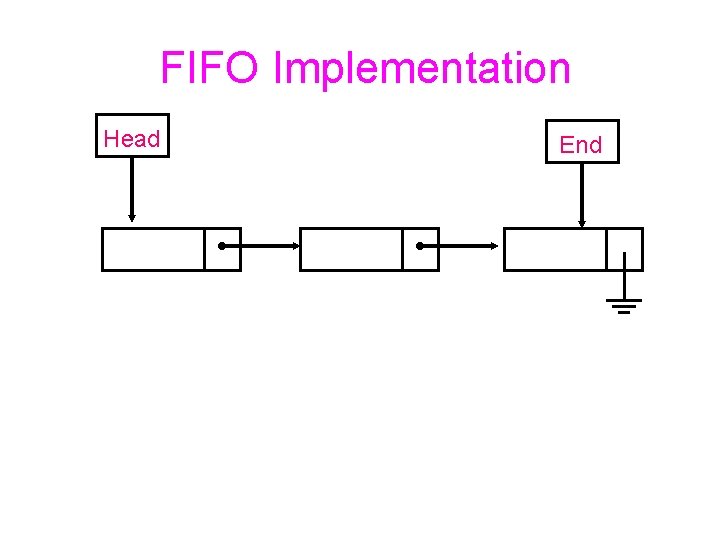
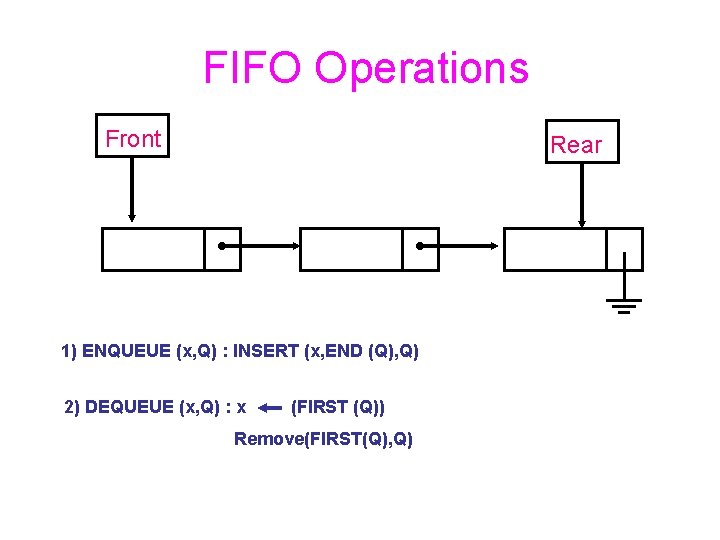
Other Data Structures for which Linked Lists are Suitable FIFO – First In First Out – Queue

FIFO Implementation Head End

FIFO Operations Front Rear 1) ENQUEUE (x, Q) : INSERT (x, END (Q), Q) 2) DEQUEUE (x, Q) : x (FIRST (Q)) Remove(FIRST(Q), Q)

Double Ended Queue Can get in or out at head or end of queue.

Linked Lists used for Compression Sparse Arrays: 613 0 7 17 0 1 2 3 4 5 0 0 6 7 8 9 0 248 26 10 11 Top 613 1 7 3 17 4 248 11 Similar scheme for multidimensions. 26 12 12