Data Structures Algorithms Stacks The Stack Definition A

Data Structures & Algorithms Stacks

The Stack: Definition • A stack is an ordered collection of items into which new items may be inserted and from which items may be deleted at one end called the TOP of the stack

Stack • The definition of stack provides for the insertion and deletion of items, so that a stack is a dynamic, constantly changing object. • How does a stack change?

Stack • New items may be put on top of the stack – In which case the top of the stack moves upward to correspond to the new highest element • Items which are at the top of the stack may be removed – In which case the top of the stack moves downward to correspond to the new highest element • Which way is up? ? ? – We must decide which end of the stack is designated as its top

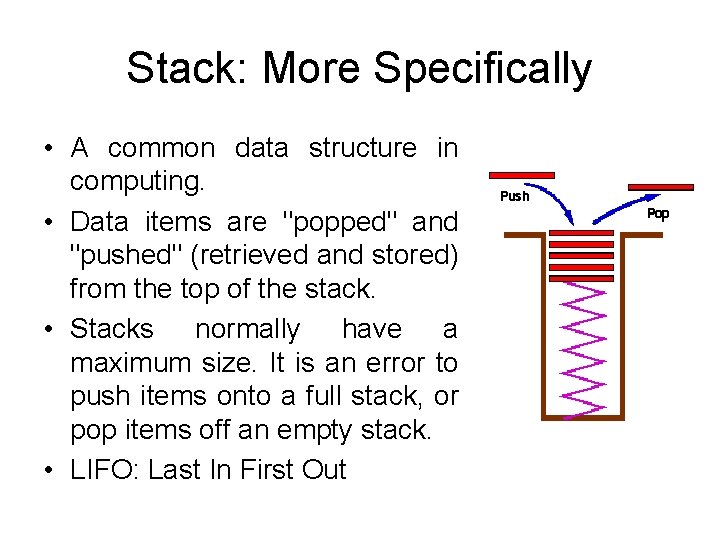
Stack: More Specifically • A common data structure in computing. • Data items are "popped" and "pushed" (retrieved and stored) from the top of the stack. • Stacks normally have a maximum size. It is an error to push items onto a full stack, or pop items off an empty stack. • LIFO: Last In First Out

Applications • Parsing of Algebraic Expression… • Banking Transaction View – You view the last transaction first • Inventory Systems like issuing students the Multi-meters… you will be issued the most recently returned item likely

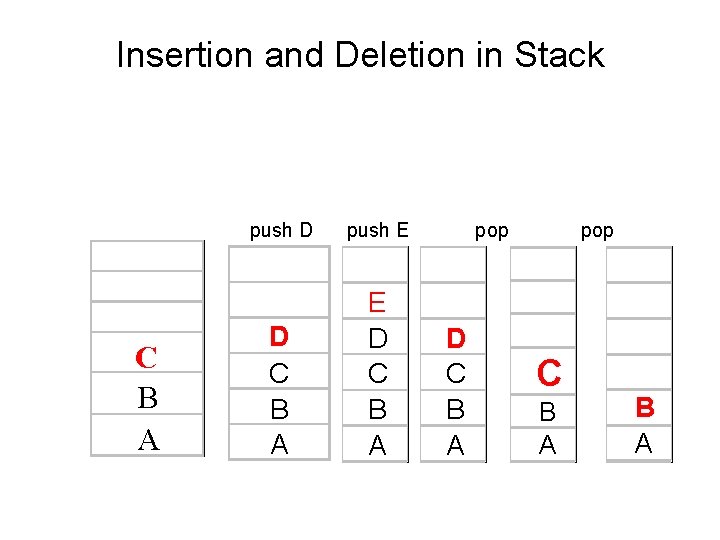
Insertion and Deletion in Stack • C is the current top element of the stack. If any new items are added to the stack, they are placed on top of C • If any new items are deleted C is deleted first C B A

Insertion and Deletion in Stack C B A push D push E D C B A pop C B A

Abstraction of a Stack • Now, let's think about a stack in an abstract way i. e. , it doesn't hold any particular kind of thing (like books) and we aren't restricting ourselves to any particular programming language or any particular implementation of a stack. • Stacks hold objects, usually all of the same type. Most stacks support just the simple set of operations we introduced above; and thus, the main property of a stack is that objects go on and come off of the top of the stack.

Operation on Stack • A Stack should have the following methods: push(item) pop( ) is. Empty() top( ) //Push an item onto the stack //Pop an item off the stack //Return true if stack is empty //Return value of top item • Because we think of stacks in terms of the physical analogy, we usually draw them vertically (so the top is really on top). • There are several ways to implement a Stack in C.

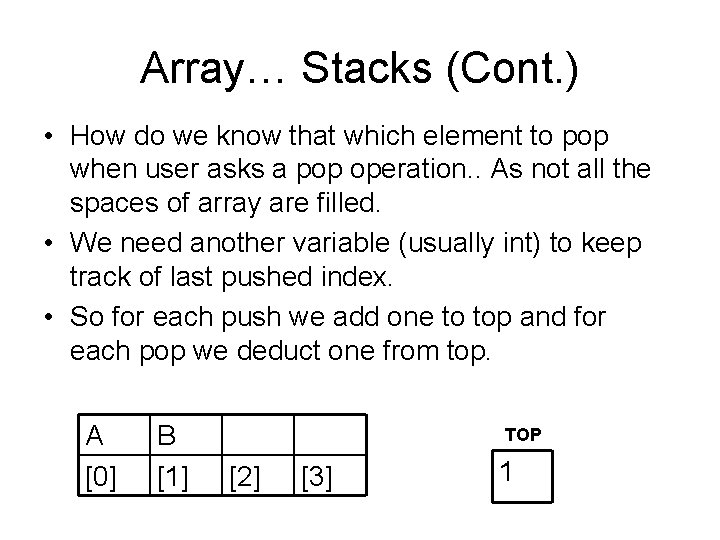
Implementing a Stack with an Array • Let's think about how to implement this stack in the C programming language. • An ordered collection of items in C is array. • First, if we want to store letters, we can use type char. Next, since a stack usually holds a bunch of items with the same type (e. g. , char), we can use an array to hold the contents of the stack. • Now, consider how we'll use this array of characters, call it contents, to hold the contents of the stack. At some point we'll have to decide how big this array is; keep in mind that a normal array has a fixed size. • Let's choose the array to be of size 4 for now. So, an array getting A, then B, will look like: A B [0] [1] [2] [3]

Array… Stacks (Cont. ) • How do we know that which element to pop when user asks a pop operation. . As not all the spaces of array are filled. • We need another variable (usually int) to keep track of last pushed index. • So for each push we add one to top and for each pop we deduct one from top. A [0] B [1] TOP [2] [3] 1

Array Stack Pictorial View say Array Name is Char. Stac. K 1 A [0] B [1] [2] [3] 2 A [0] B [1] C [2] [3] 3 A [0] B [1] C [2] 2 A [0] B [1] C [2] D [3] • Push(Char. Stack, ’C’) • Push(char. Stack, ‘D’) • Pop(char. Stack)

• Push Concerns – What if when the stack is full? • Pop Concerns – What if the stack is empty? • Solution – Before any push check if the stack is already filled or not. If it is filled then generate error message e. g. , Stack Overflow – Before pop check if stack is not already empty

A Sample Program (Push Pop using Array) #include<stdio. h> #include<conio. h> #include<stdlib. h> #include <iostream. h> #define length 10 int top=-1; int stack[length]; void main() { int ch; do{ cout << endl << "1. push"; cout << endl << "2. pop"; cout << endl << "3. exit"; cout << endl << "enter choice"; cin >> ch; switch(ch) { case 1: push(); list. Stack(); break; case 2: cout << "data poped= " << pop(); list. Stack(); break; case 3: exit(0); } } while(1); getch(); }

A Sample Program (Push Pop using Array) void push() { int data; if(top+1==length) { cout << "stack overflown Cannot enter new data"; return; } top++; cout << "enter the data "; cin >> data; stack[top]=data; } int pop() { int temp. Var; if(top==-1)//we can also make is. Empty() { cout << "stack is underflow (Empty)"; return(-1); } temp. Var=stack[top]; top--; return(temp. Var); } void list. Stack() { cout << endl << "The stack is" << endl ; for(int i=top; i>=0; i--) cout << stack[i] << endl; }

Stack in Problem Solving • • • Consider a mathematical expression that includes several sets of nested parenthesis, e. g. ( x + (y – (a +b)) ) We want to ensure that parenthesis are nested correctly and the expression is valid Validation 1. There is an equal number of right and left parentheses 2. Every right parenthesis is preceded by a matching left parenthesis

Expressions • (A+B) * C • A + B) • (A+B] Valid Invalid

Rules • Each left parentheses is the opening scope. • Each right parenthesis is a closing scope. • The number of left parentheses encountered whose matching right parentheses have not been encountered is nesting depth at that point. • Parentheses count = 0 at the end means that no scopes have been left open and left and right parentheses exactly match. • The parentheses count at any time should never become negative. IF negative then its error.

Expressions • ((A+B) • 122221 Error • (A*B) • 11110 Right • A*B( • 0001 Error

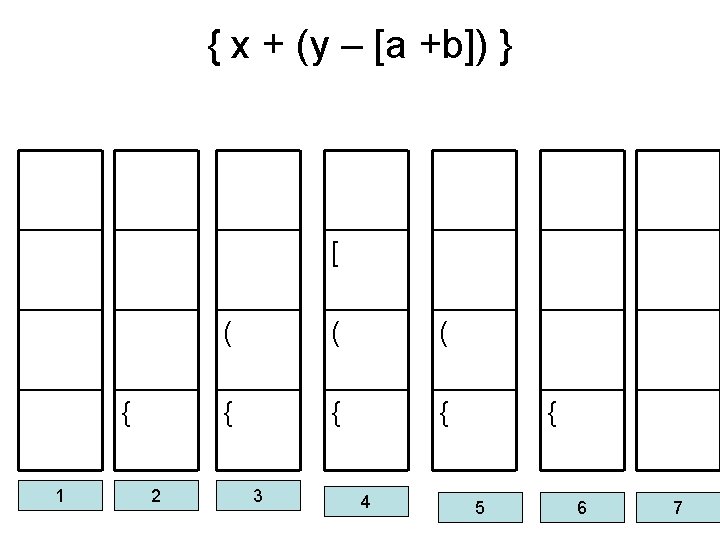
Parsing Parenthesis • Let us change the problem slightly • Three different kinds of scope delimiters exist e. g. { x + (y – [a +b]) } • The scope ender must be of same type as scope opener • It is necessary to keep track of not only the count of scope but also the types • A stack may be used to keep track of the types of scopes encountered

Stacks in Expression Validation • Whenever a scope opener is encountered it is pushed into the stack • Whenever a scope ender is encountered the stack is examined • If the stack is empty the scope ender does not have a matching opener and string is invalid • If stack is not empty we pop an item and check if it corresponds to scope ender • If match occurs we continue, at the end of the string the stack must be empty

Pusedo-Code Valid = true S = the empty stack // array of chars say char s[100] While (we have not read the entire string) { read the next symbol (symb) of the string; if (symb == ‘(‘ || symb == ‘[‘ || symb == ‘{‘) push (s, symb); if (symb == ‘)‘ || symb == ‘]‘ || symb == ‘}‘) if (empty(s)) valid = false; else { I = pop (s); if ( I is not the matching opener of symb) valid = false; } // end of else } //end while If (valid) cout << “Valid String” << endl; Else cout << “not a valid string”