Data Structures Algorithms Sorting Sorting Recall Selection Sort

Data Structures & Algorithms Sorting

Sorting Recall • Selection Sort • Insertion Sort • Merge Sort Now consider • Bubble Sort • Shell Sort • Quick Sort

Bubble Sort Keep passing through the array Exchange adjacent elements that are out of order Until array is sorted void bubble. Sort(Item a[], int l, int r) { for (int i = l; i < r; ++i) for (int j = r; j > i; --j) comp. Exch(a[j-1], a[j]); }

Bubble Sort A L G O R I T H M * A G L H O I A L G O R I H T A L G O R H I A L A M A G L H I T M A G H L I O R M T G O H R I T M A G H L I O M R T L G H O R I T M A G H L I M O R T A L G H O R I T M A G H I L M O R T A G L H O R I M T * R M T O R M T * *

Bubble Sort Property 6. 3: Bubble. Sort uses about N 2/2 comparisons and N 2/2 exchanges on the average and in the worst case. void bubble. Sort(Item a[], int l, int r) { for (int i = l; i < r; ++i) for (int j = r; j > i; --j) comp. Exch(a[j-1], a[j]); } http: //www. sorting-algorithms. com/bubble-sort

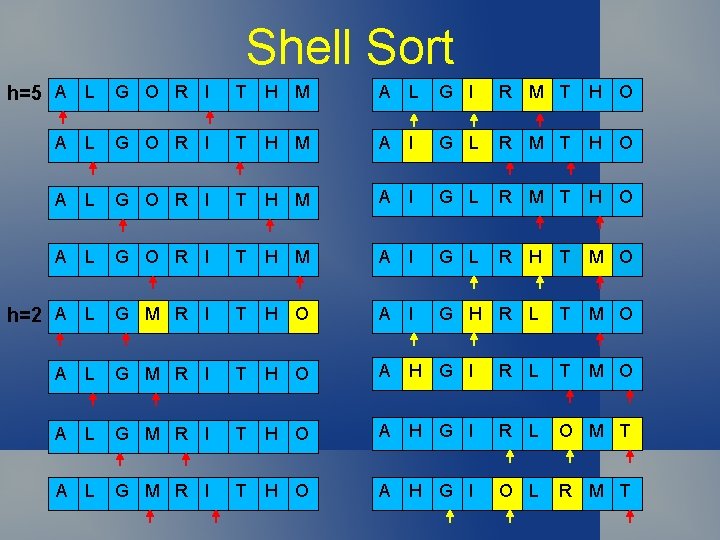
Shell Sort Make array h-sorted: h-sorted means the h sub-arrays are sorted (with sub-array i being elements in a[j] where j%h == i) Exchange distant elements that are out of order Decrease h until array is sorted (h = 1) Step sequence is not obvious, and there are many interactions – geometric best Knuth recommended s[i+1] = 3*s[i]+1

Shell Sort Make array h-sorted for decreasing h: void shell. Sort(Item a[], int l, int r) { int h; for (h = 1; h <= (r-l)/9; h = 3*h+1); for ( ; h > 0; h/= 3) for (int i = l+h; i <= r; ++i) { int j = i; Item v = a[i]; while (j >= l+h && v < a[j-h]) { a[j] = a[j-h]; j -= h; } a[j] = v; } }

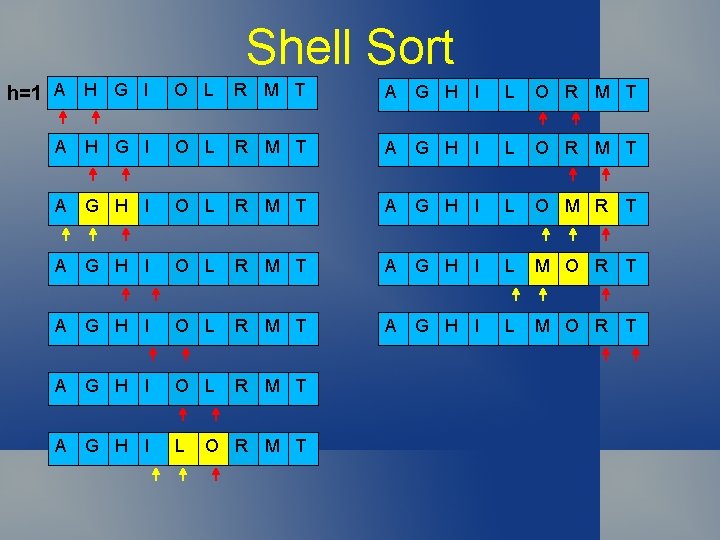
Shell Sort h=5 A L G O R I T H M A L G I R M T H O A L G O R I T H M A I G L R H T M O h=2 A L G M R I T H O A I G H R L T M O A L G M R I T H O A H G I R L T A L G M R I T H O A H G I R L O M T A L G M R I T H O A H G I O L R M T

Shell Sort h=1 A H G I O L R M T A G H I L O R M T A G H I O L R M T A G H I L O M R T A G H I O L R M T A G H I L M O R T A G H I O L R M T A G H I L O R M T

Shell. Sort Property 6. 7: The result of h-sorting a file that is k-ordered is a file that is both h- and kordered. Property 6. 8: Shell. Sort does less than N(h-1)(k -1)/g comparisons to g-sort a file that is h- and k-ordered, provided that h and k are relatively prime Property 6. 9: Shell. Sort does less than O(N 3/2) comparisons for the Knuth sequence. http: //www. sorting-algorithms. com/shell-sort

Sorting with Linked Lists Can sort with linked lists Need sorting algorithm to process sequentially – in same manner that link lists support e. g. , selection sort, insertion sort, bubble sort Insertion is fast (adjust some links – constant time) Shift is fast (just insert!) Never change key or information in nodes, ONLY change links!

Key-Indexed Counting When keys are all in some small range (relative to the number of items) Can use the keys as indices e. g. , sort N items with distinct keys in range 0 to N What if there are duplicate keys?

Key-Indexed Counting Sort N items with keys in range 0 to M-1 Let count[i] be the number of items with a key value = i (can find in one pass) Let rank[i] be the number of items with a key value < i (partial sums of counts) Put item with key k into array between rank[k] and rank[k+1] Algorithm due to Seward (1954)

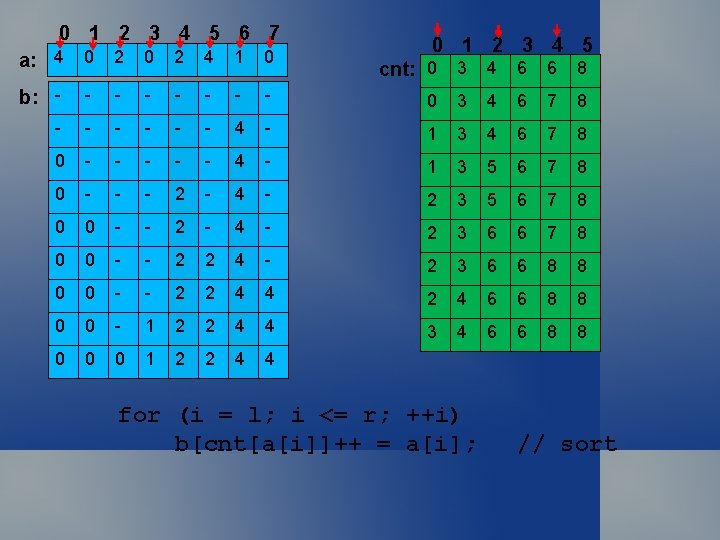
Key-Indexed Counting void distcount(int a[], int l, int r) { int I, j, cnt[M]; // M = # of keys static int b[max. N]; for (j = 0; j < M; ++j) cnt[j] = 0; for (i = l; i <= r; ++i) ++cnt[a[i]+1]; // count keys for (j = 1; j < M; ++j) cnt[j] += cnt[j-1]; // comp ranks for (i = l; i <= r; ++i) b[cnt[a[i]]++ = a[i]; // sort for (i = l; i <= r; ++i) a[i] = b[i-l]; // copy back }

Key Indexed Sort 0 1 2 3 4 5 6 7 a: 4 0 2 4 1 0 0 1 2 3 4 5 cnt: 0 0 0 1 0 0 0 1 0 1 0 2 0 1 0 2 0 2 1 2 0 3 1 2 0 2 for (j = 0; j < M; ++j) cnt[j] = 0; for (i = l; i <= r; ++i) ++cnt[a[i]+1]; // count keys

Key Indexed Sort 0 1 2 3 4 5 6 7 a: 4 0 2 4 1 0 0 1 2 3 4 5 cnt: 0 3 1 2 0 2 0 3 4 6 0 2 0 3 4 6 6 8 for (j = 1; j < M; ++j) cnt[j] += cnt[j-1]; // comp ranks

0 1 2 3 4 5 6 7 0 1 2 3 4 5 a: 4 0 2 4 1 0 b: - - - - 0 3 4 6 7 8 - - - 4 - 1 3 4 6 7 8 0 - - - 4 - 1 3 5 6 7 8 0 - - - 2 - 4 - 2 3 5 6 7 8 0 0 - - 2 - 4 - 2 3 6 6 7 8 0 0 - - 2 2 4 - 2 3 6 6 8 8 0 0 - - 2 2 4 4 2 4 6 6 8 8 0 0 - 1 2 2 4 4 3 4 6 6 8 8 0 0 0 1 2 2 4 4 cnt: 0 3 4 6 6 8 for (i = l; i <= r; ++i) b[cnt[a[i]]++ = a[i]; // sort

Key-Indexed Counting Prop. 6. 12: Key-Indexed Counting is a lineartime sort, provided the range of distinct key values is within a constant factor of the file size. Prf: Each item is moved twice (once to the temp array b, once back to a). Each key is referenced twice (once for counts, once for distribution). The other two loop that build the counts and ranks are linear in M.