Data Structures Algorithms Recursion and Trees Recursion Fundamental

Data Structures & Algorithms Recursion and Trees

Recursion Fundamental concept in math and CS Recursive definition Defined in terms of itself a. N = a*a. N-1, a 0 = 1 Recursive function Calls itself int exp(int base, int pow) { return (pow == 0 ? 1 : base*exp(base, pow 1));

Recursion Recursive definition (and function) must: 1. have a base case – termination condition 2. always call a case smaller than itself All practical computations can be couched in a recursive framework! (see theory of computation)

Recursion Recursively defined structures e. g. , binary tree Base case: Empty tree has no nodes Recursion: None-empty tree has a root node with two children, each the root of a binary tree

Recursion Widely used in CS and with trees. . . Mathematical recurrences Recursive programs Divide and Conquer Dynamic Programming Tree traversal DFS

Recursive Algorithms • • Recursive algorithm – solves problem by solving one or more smaller instances of same problem Recurrence relation – factorial – N! = N(N-1)!, for N > 0, with 0! = 1. – In C++, use recursive functions Int factorial(int N) { if (N == 0) return 1; return N*factorial(N-1); }

Recursive Algorithms • • BTW, can often also be expressed as iteration E. g. , can also write N! computation as a loop: int factorial(int N) { for (int t = 1, i = 1; i <= N; ++i) t *= i; return t; }

Euclid’s Algorithm Euclid's Algorithm is one of the oldest known algorithms Recursive method for finding the GCD of two integers int gcd(int m, int n) { // expect m >= n if (n == 0) return m; return gcd(n, m % n); } Base case Recursive call to smaller instance

Divide & Conquer Recursive scheme that divides input into two (or some fixed number) of (roughly) equal parts Then makes a recursive call on each part Widely used approach Many important algorithms Depending on expense of dividing and combining, can be very efficient

Divide & Conquer Example: find the maximum element in an array a[N] (Easy to do iteratively. . . ) Base case: Only one element – return it Divide: Split array into upper and lower halves Recursion: Find maximum of each half Combine results: Return larger of two maxima

Divide & Conquer Property 5. 1: A recursive function that divides a problem of size N into two independent (non-empty) parts that it solves, recursively calls itself less than N times. Prf: T(1) = 0 T(N) = T(k) + T(N-k) + 1 for recursive call on size N divided into one part of size k and the other of size N-k Induct!

Towers of Hanoi 3 pegs N disks, all on one peg Disks arranged from largest on bottom to smallest on top Must move all disks to target peg Can only move one disk at a time Must place disk on another peg Can never place larger disk on a smaller one Legend has it that the world will end when a certain group of monks finishes the task in a temple with 40 golden disks on 3 diamond pegs

Towers of Hanoi Which peg should top disk go on first? Target peg

Towers of Hanoi How many moves does this take?

Towers of Hanoi Property 5. 2: The recursive d&c algorithm for the Towers of Hanoi problem produces a solution that has 2 N – 1 moves. Prf: T(1) = 1 T(N) = T(N-1) + 1 + T(N-1) = 2 T(N-1) + 1 = 2 N – 1 by induction

Divide & Conquer Two other important D&C algorithms: Binary search Merge. Sort Algorithm Metric Recurrence Approx. Soln. Binary Search comparisons C(N) = C(N/2)+1 Merge. Sort recursive calls A(N) = 2 A(N/2) + 1 N Merge. Sort comparisons C(N) = 2 C(N/2) + N N lg N

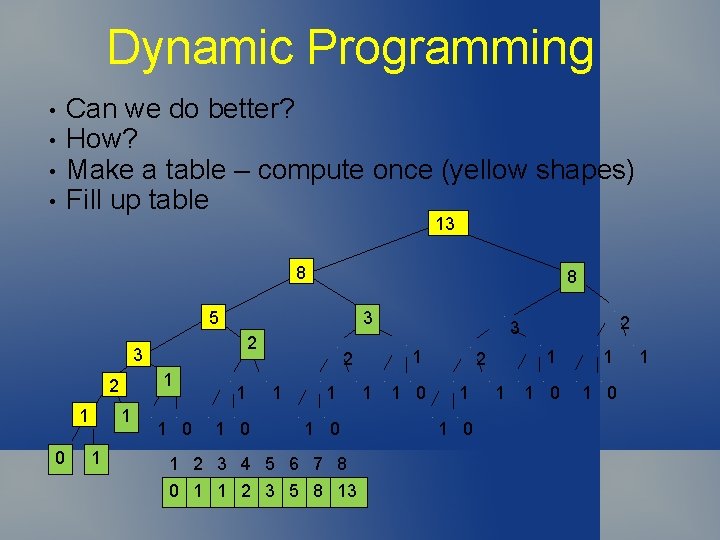
Dynamic Programming In Divide & Conquer, it is essential that the subproblems be independent (partition the input) When this is not the case, life gets complicated! Sometimes, we can essentially fill up a table with values we compute once, rather than recompute every time they are needed. This is Dynamic Programming Issue – table may be too big!

Dynamic Programming Fibonacci Numbers: F[0] = 0 l F[1] = 1 l F[N] = F[N-1] + F[N-2] l Horribly inefficient implementation: int F(int N) { if (N < 1) return 0; if (N == 1) return 1; return F(N-1) + F(N-2); }

Dynamic Programming • • How bad is this code? How many calls does it make to itself? F(N) makes F(N+1) calls! Exponential!!!! 13 8 5 5 3 2 1 1 0 1 2 1 1 1 0 1 2 3 1 0 2 1 1 0 1

Dynamic Programming • • Can we do better? How? Make a table – compute once (yellow shapes) Fill up table 13 8 8 5 3 2 3 1 2 1 0 1 2 1 1 1 0 1 2 3 4 5 6 7 8 0 1 1 2 3 5 8 13 1 2 3 1 0 2 1 1 0 1

Dynamic Programming Property 5. 3: Dynamic Programming reduces the running time of a recursive function to be at most the time it takes to evaluate the functions for all arguments less than or equal to the given argument, treating the cost of a recursive call as a constant.

Trees A mathematical abstraction Central to many algorithms Describe dynamic properties of algorithms Build and use explicit tree data structures Examples: Family tree of descendants Sports tournaments (Who's In? ) Organization Charts (Army) Parse tree of natural language sentence File systems

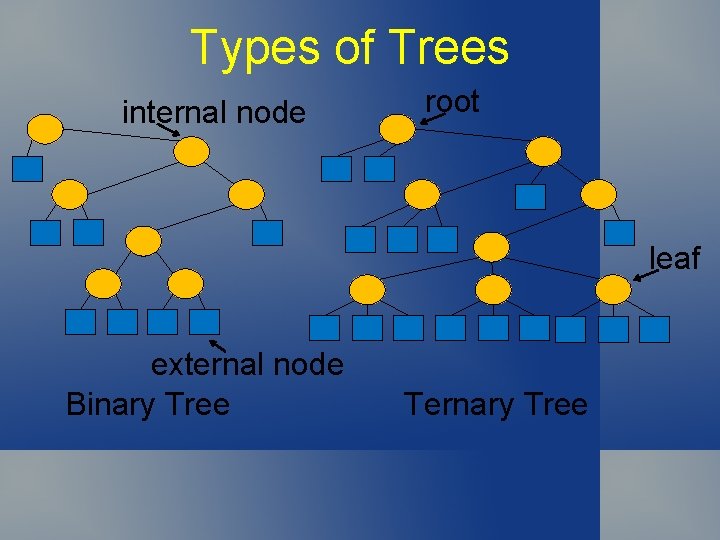
Types of Trees • • Trees Rooted trees Ordered trees M-ary trees and binary trees Defn: A tree is a nonempty collection of vertices and edges such that there is exactly one path between each pair of vertices. • Defn: A path is a list of distinct vertices such that successive vertices have an edge between them • Defn: A graph in which there is at most one path between each pair of vertices is a forest. •

Types of Trees internal node root leaf external node Binary Tree Ternary Tree

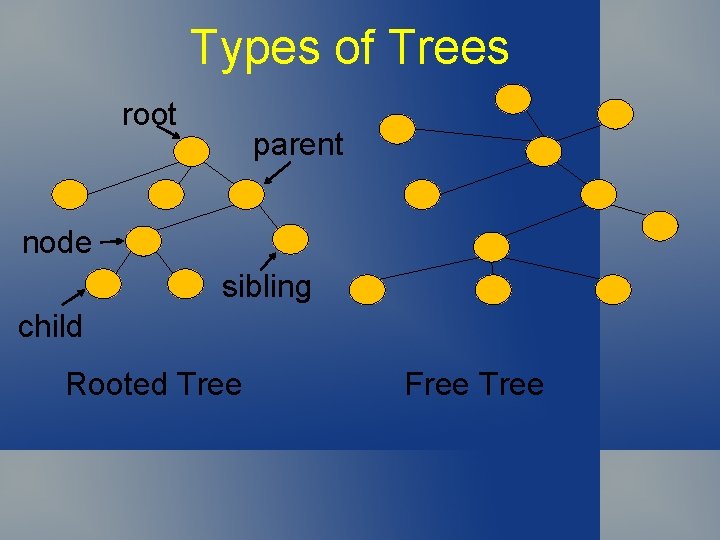
Types of Trees root parent node sibling child Rooted Tree Free Tree

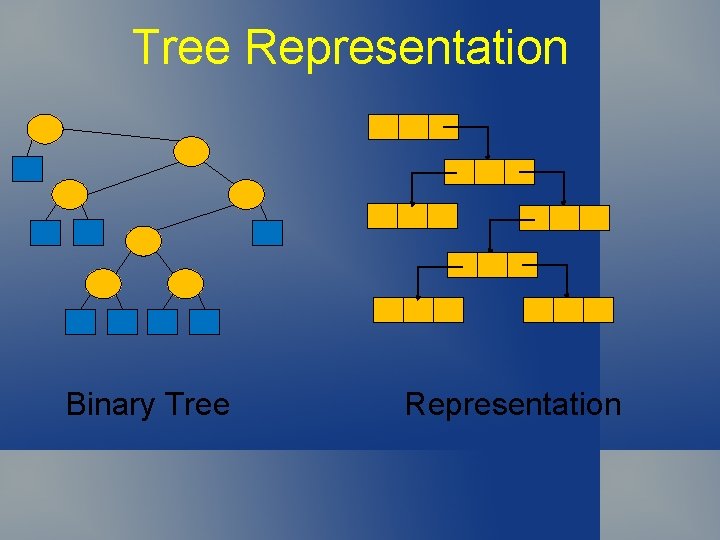
Tree Representation Binary Tree Representation

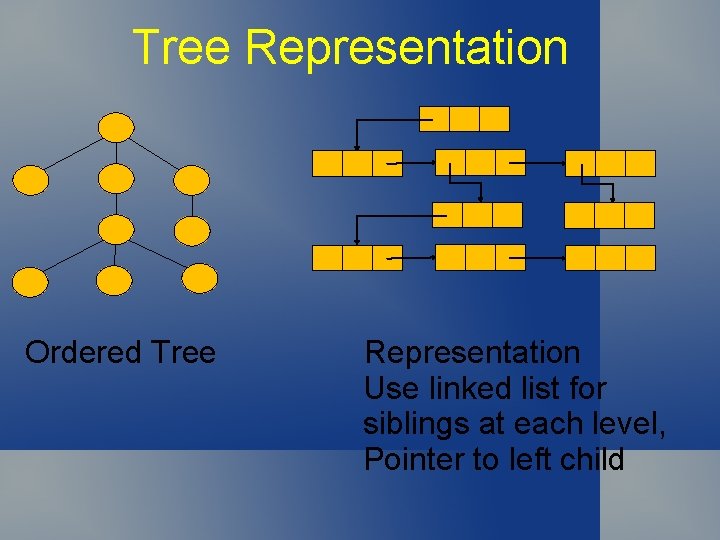
Tree Representation Ordered Tree Representation Use linked list for siblings at each level, Pointer to left child

Properties of Trees • • • A binary tree with N internal nodes has • N+1 external nodes A binary tree with N internal nodes has 2 N links: N-1 to internal nodes and N+1 to external nodes The level of a node is one higher than the level of its parent, with the root at level 0. The path length of a tree is the sum of the levels of all the tree’s nodes The internal path length is the sum of levels of internal nodes; external path length is sum of levels of external nodes.

Properties of Trees The external path length of any binary tree with N nodes is 2 N greater than the internal path length • The height of a binary tree with N internal nodes is at least lg N and at most N-1. • The internal path length of a binary tree with N internal nodes is at least N lg(N/4) and at most N(N-1)/2. •

Tree Traversal • Given pointer to a tree, visit every node in the tree systematically • Inorder: Visit the left subtree, visit the root, then visit the right subtree Preorder: Visit the root, visit the left subtree, visit the right subtree. Postorder: Visit the left subtree, visit the right subtree, visit the root. • •

Tree Traversal • • Generic recursive traversal code Preorder? Inorder? Postorder? void traverse(link h, void visit(link)) { if (h == NULL) return; visit(h); traverse(h->left, visit); traverse(h->right, visit); }

Tree Traversal • • Generic iterative traversal code Preorder? Inorder? Postorder? void traverse(link h, void visit(link)) { STACK<link> s(max); s. push(h); while (!s. empty()) { visit(h = s. pop()); if (h->right != 0) s. push(h->right); if (h->left != 0) s. push(h->left); } }

Tree Traversal • • Generic iterative traversal code Level order = top to bottom, left to right void traverse(link h, void visit(link)) { QUEUE<link> q(max); q. put(h); while (!q. empty()) { visit(h = q. get()); if (h->left != 0) q. put(h->left); if (h->right != 0) q. put(h->right); } }

Basic Tree Algorithms • • Count number of nodes Compute height Compute internal path length Display tree int count(link h) { if (h == NULL) return 0; return 1 + count(h->left) + count(h->right); }

Basic Tree Algorithms • • Count number of nodes Compute height Compute internal path length Display tree int height(link h) { if (h == NULL) return -1; int u = height(h->left); int v = height(h->right); return 1 + (u > v ? u : v); }

Basic Tree Algorithms • Display tree (order? ) void printnode(Item x, int h) { for (int i=0; i<h; ++i) cout << “ “; cout << x << endl; } void show(link t, int h) { if (t == NULL) { printnode(‘*’, h); return; } show(h->left, h+1); printnode(t->item, h); show(h->right, h+1); }

Tree Algorithms • • Tournament construction Start with array (list of competitors) Develop into tree with matches Divide and conquer: • Split in half • Make tourney with left (first) half • Make a tourney with right (last) half • Make a new node with links to the two tourneys • Single item tourney = leaf with that item • Item in interior nodes? Winner of tourney!

Graph Traversal • • • Recursive Graph Traversal DFS = Depth-First Search Generalization of tree traversal methods Basis for many algorithms for processing graphs Code: • Starting at any node v • Visit v • Recursively visit each unvisited neighbor of v If graph is connected, will visit every node Need to be able to mark nodes as visited Don’t need to do this for trees (why not? ) Set of edges on which calls are made forms a spanning tree

Graph Traversal Recursive Graph Traversal: DFS Property 5. 10: DFS requires time O(V+E) in a graph with V vertices and E edges using the adjacency lists representation Adjacency list representation: one list node corresponding to each edge in the graph, and one list head pointer corresponding to each vertex in the graph. • • void traverse(int k, void visit(int)) { visit(k); visited[k] = TRUE; for (link t=adj[k]; k!=0; t = t->next) if (!visited[t->v]) traverse(t->v, visit); }

Graph Traversal • BFS in graph void traverse(int k, void visit(int)) { QUEUE<link> q(V*V); q. put(k); while (!q. empty()) { if (!visited[k = q. get()] ) { visit(k); visited[k] = 1; for (link t=adj[k]; t!=0; t=t->next) if (!visited[t->v]) q. put(t->v); } } }