Data Structures Algorithms Lecture 6 Elementary Data Structures

Data Structures & Algorithms Lecture 6: Elementary Data Structures

Abstract Data Types

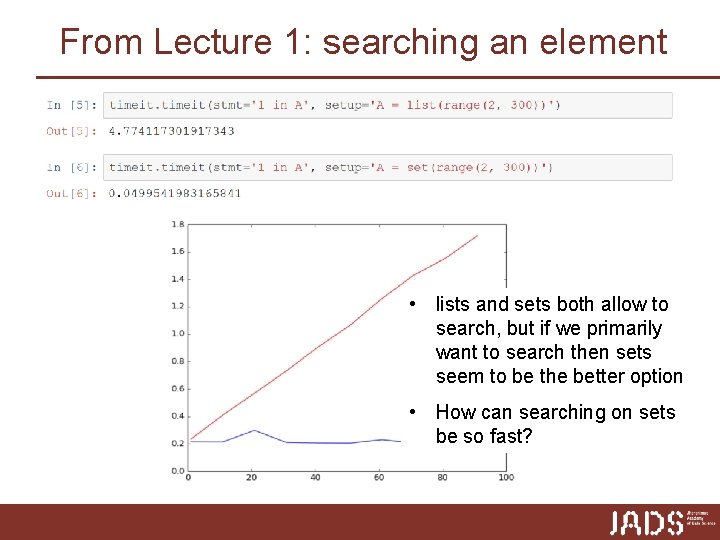
From Lecture 1: searching an element • lists and sets both allow to search, but if we primarily want to search then sets seem to be the better option • How can searching on sets be so fast?

Abstract data types and Data Structures Data Structure a way to store and organize data to facilitate access and modifications. Ex. array, linked list, later in the course: hash table, heap, … Abstract Data Type (ADT) a set of data values and associated operations that are precisely specified independent of any particular implementation. Ex. stack, queue, … later in the course: dictionary, priority queue, … p ADT describe the functionality of data structures p Data structures implement ADT n how is the data stored? n which algorithms implement the operations?

Abstract data types and Data Structures Abstract Data Types are defined independent of their implementation. p We can focus on solving the problem instead of the implementation p p details Reduce logical errors by preventing direct access to the implementation Implementation can be changed We can have multiple, different implementations for the same data type Easier to manage and divide larger programs into smaller modules

Stacks

Stacks Stack Stores a set S of elements with insertions and deletions follow a LIFO (last-in, first-out) scheme Operations push(S, x): inserts element x into S pop(S): removes and returns the element last inserted into S size(S): returns the number of elements in S is. Empty(S): indicates whether S is the empty set

Applications p Direct applications n Page-visited history in a Web browser n Undo sequence in a text editor n Chain of method calls in a language that supports recursion p Indirect applications n Auxiliary data structure for algorithms n Component of other data structures

Array-Based Stack … S 0 1 2 t p we add elements from left to right p a variable keeps track of the index of the top element Stack(): data = array of size 15 count = 0 p capacity of stack is capped to size of array

Array-Based Stack(): data = array of size 20 count = 0 p How can we implement the operations size, is. Empty, push and pop? p What is the running time of the operations?

Growable Array-based Stack p Fixed-capacity stack: fast but not very useful p How can we make an array-based stack that has unlimited capacity? n Incremental strategy: increase the size of the array by a constant c when capacity is reached n Doubling strategy: double the size of the array when capacity is reached p Problem: arrays cannot be resized. You can only copy over elements to a new array

Growable Array-based Stack(): data = array size 20 count = 0 capacity = 20 p What’s the runtime of push? n when the stack doesn’t expand? O(1) n when it does expand? Incremental: O(n) Doubling: O(n)

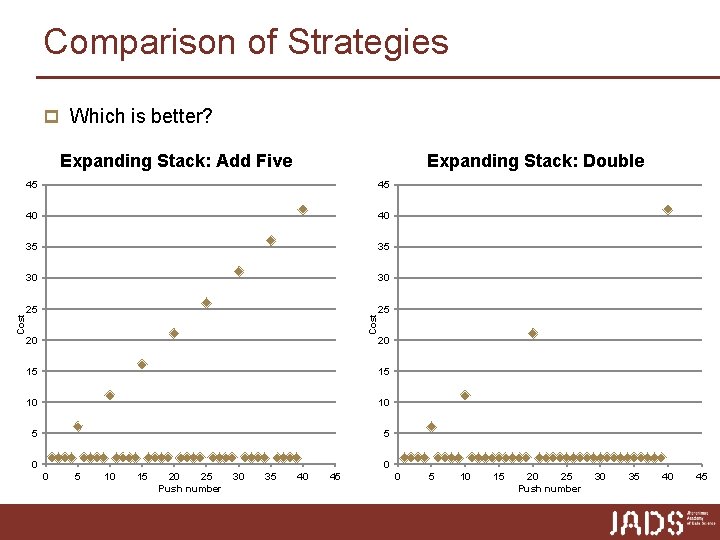
Comparison of Strategies p Which is better? Expanding Stack: Double 45 45 40 40 35 35 30 30 25 25 Cost Expanding Stack: Add Five 20 20 15 15 10 10 5 5 0 0 0 5 10 15 20 25 Push number 30 35 40 45

Comparison of Strategies p Which is better? p Compare the incremental strategy and the doubling strategy by analyzing the total time T(n) needed to perform a series of n push operations p Amortized (average) analysis: time required to perform a sequence of operations averaged over all the operations performed n amortized time of a push operation: T(n)/n

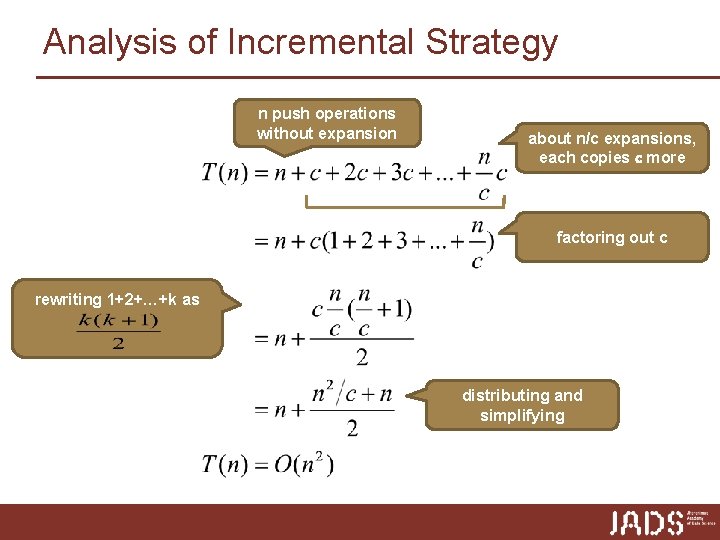
Analysis of Incremental Strategy n push operations without expansion about n/c expansions, each copies c more factoring out c rewriting 1+2+…+k as distributing and simplifying

Comparison of Strategies p Amortized (average) analysis: time required to perform a sequence of operations averaged over all the operations performed n amortized time of a push operation: T(n)/n p Incremental Strategy: n Total time T(n) of a series of n push operations is O(n 2) for incremental n Amortized time of a single push operation is therefore T(n)/n = O(n) using the incremental strategy for an expanding stack

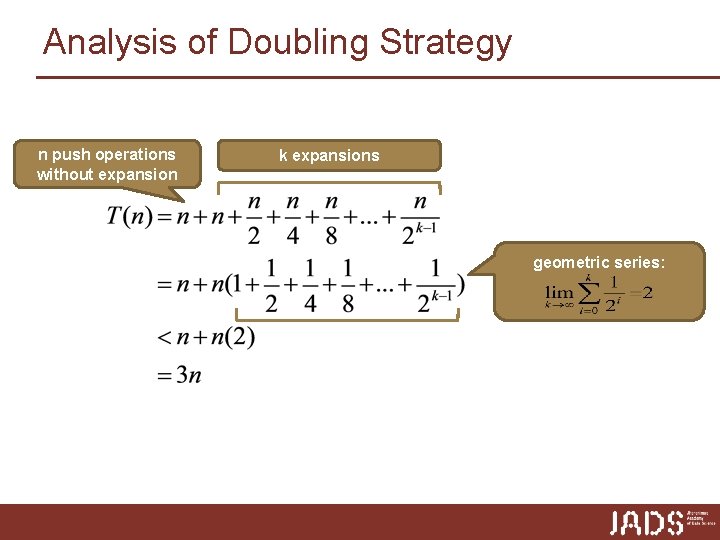
Analysis of Doubling Strategy n push operations without expansion k expansions geometric series:

Comparison of Strategies p Amortized (average) analysis: time required to perform a sequence of operations averaged over all the operations performed n amortized time of a push operation: T(n)/n p Incremental Strategy: n Total time T(n) of a series of n push operations is O(n 2) for incremental n Amortized time of a single push operation is therefore T(n)/n = O(n) using the incremental strategy for an expanding stack p Doubling Strategy: n Total time T(n) of a series of n push operations is O(n) for incremental n Amortized time of a single push operation is therefore T(n)/n = O(1) using the incremental strategy for an expanding stack

Stacks/Growable Arrays in Python p The list data type in Python is based on a growable array with doubling strategy p How long do the following operations take for Python lists? O(1) amortized O(n-i+1) amortized s. append(x) appends x to the end of the sequence (same as s[len(s): len(s)] = [x]) s. insert(i, x) inserts x into s at the index given by i (same as s[i: i] = [x]) s. pop([i]) retrieves the item at i and also removes it from s O(n-i) amortized s. remove(x) remove the first item from s where s[i] == x O(n) p Why is pop amortized? Array may shrink again. p As implementation of the Stack ADT: pop/push/size/is. Empty O(1)

Stacks/Growable Arrays in Python p A stack implemented using a Python list (I am not explaining classes, just note the operations):

Queues

Queues Queue Stores a set S of elements with insertions and deletions follow a FIFO (first-in, first-out) scheme Operations enqueue(S, x): inserts element x into S dequeue(S): removes and returns the element first inserted into S size(S): returns the number of elements in S is. Empty(S): indicates whether S is the empty set

Growable Array-based Queue p We can also implement a queue using an growing array, but with a slight complication p Unlike a stack, we need to keep track of the head and the tail of the queue p What happens if the tail reaches the end of the array, but there’s still room at the front? Is the queue full? 0 1 2 head tail

Growable Array-based Queue p Wrap the queue! tail head 0 1 2 p Expand the array when queue is completely full n When copying, “unwind” the queue so the head starts back at 0 dequeue(): enqueue(x): if size == 0: if size == capacity: double array and copy contents error(“queue empty”) element = data[head] reset head and tail pointers data[tail] = x head = (head + 1) % capacity tail = (tail + 1) % capacity size++ size-- head return element tail

Queues in Python p Do Python lists provide an efficient implementation of Queues if used “directly”? p No: n enqueue(x): s. append(x) in O(1) amortized time, but n dequeue(): s. pop(0) in O(n) time p Deques (double-ended Queues) are provided as collections. deque p deques are not implemented using arrays but doubly-linked lists

Linked Lists

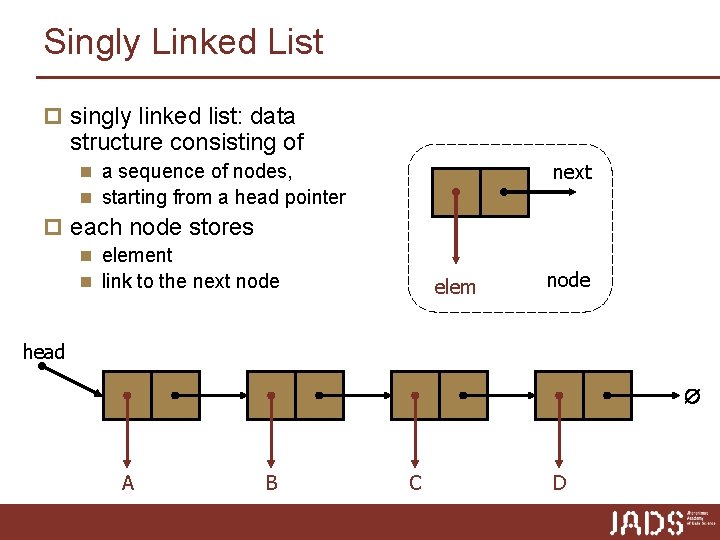
Singly Linked List p singly linked list: data structure consisting of next n a sequence of nodes, n starting from a head pointer p each node stores n element n link to the next node elem node head A B C D

Implementing a Singly Linked List How do we insert/delete efficiently in a Singly Linked List?

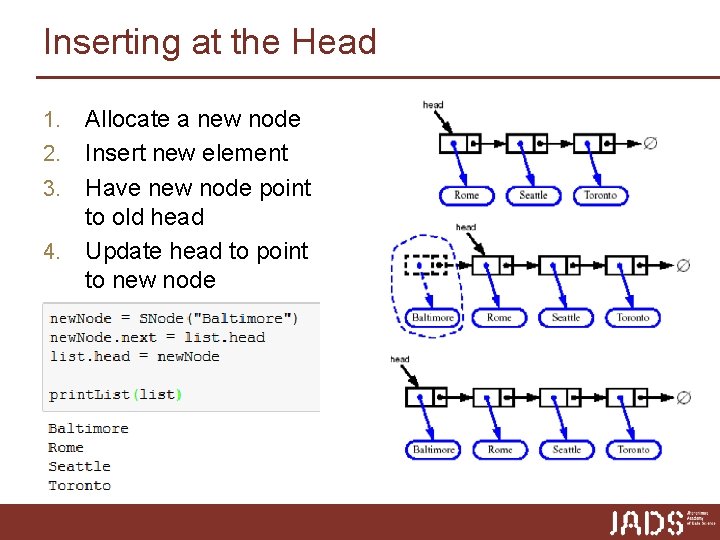
Inserting at the Head Allocate a new node 2. Insert new element 3. Have new node point to old head 4. Update head to point to new node 1.

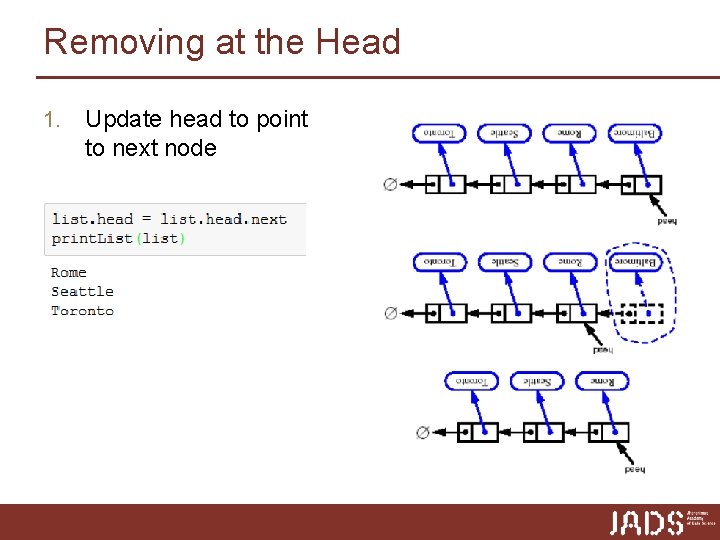
Removing at the Head 1. Update head to point to next node

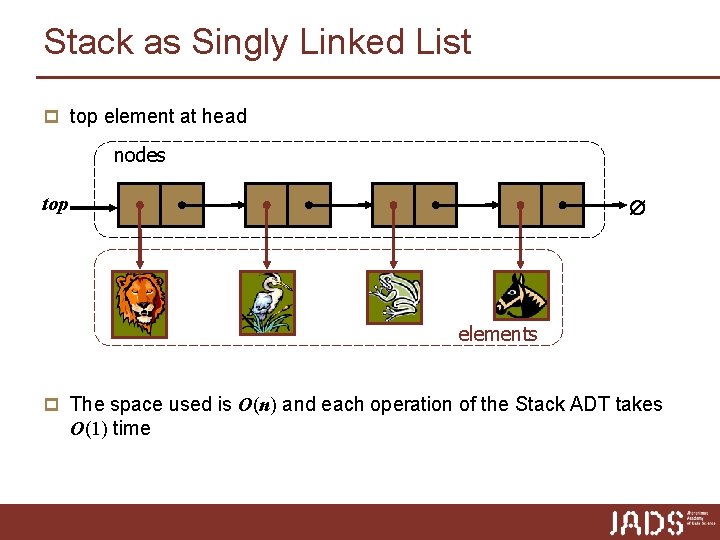
Stack as Singly Linked List p top element at head nodes top elements p The space used is O(n) and each operation of the Stack ADT takes O(1) time

Stack as Singly Linked List How do we implement a Queue?

Inserting at the Tail (at the End) 1. 2. 3. 4. 5. Allocate a new node Insert new element Have new node point to null Have old last node point to new node Update tail to point to new node p requires pointer to tail: list. tail p with pointer also O(1)

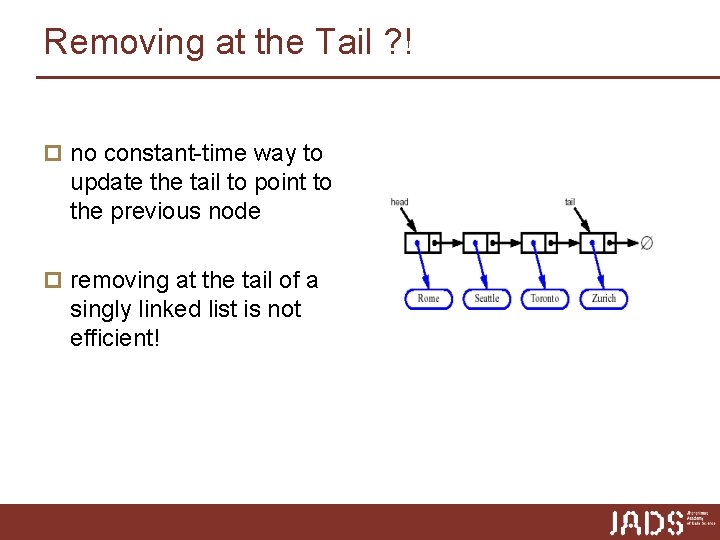
Removing at the Tail ? ! p no constant-time way to update the tail to point to the previous node p removing at the tail of a singly linked list is not efficient!

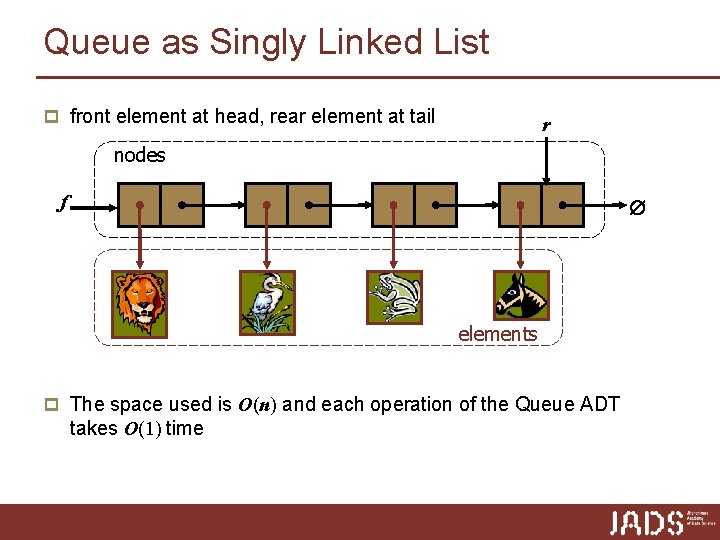
Queue as Singly Linked List p front element at head, rear element at tail r nodes f elements p The space used is O(n) and each operation of the Queue ADT takes O(1) time

Queue as Singly Linked List How do we implement a Deque (pop/push at both ends)?

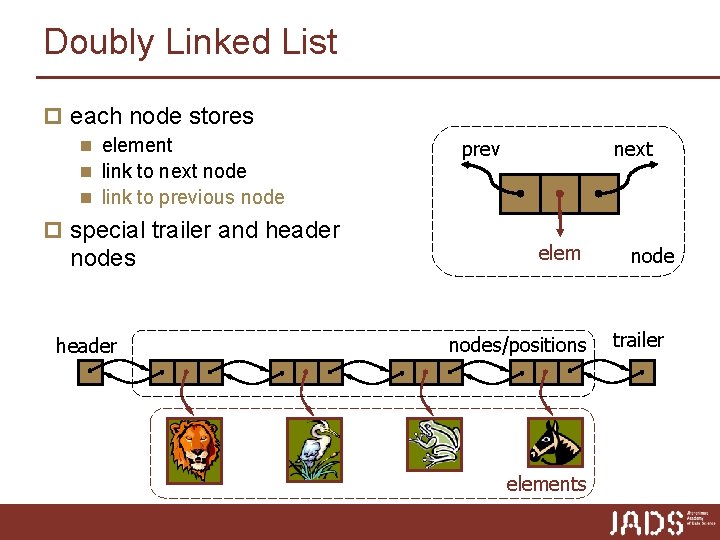
Doubly Linked List p each node stores n element n link to next node n link to previous node p special trailer and header nodes header prev next elem nodes/positions elements node trailer

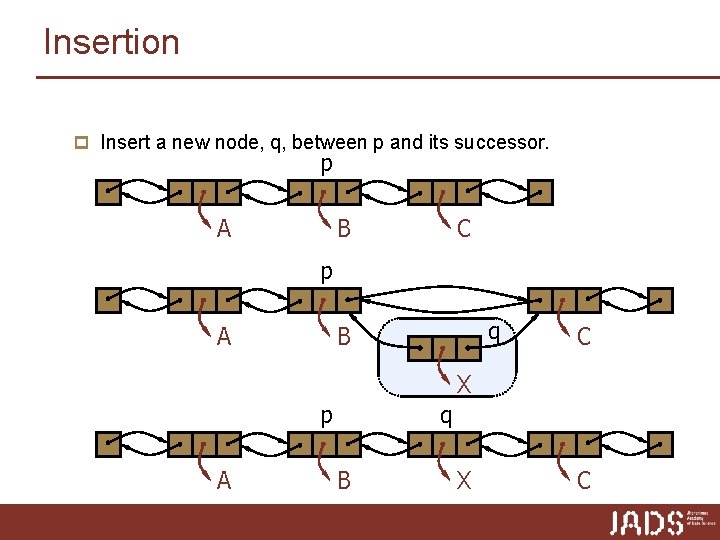
Insertion p Insert a new node, q, between p and its successor. p A B C p A q B C X p A q B X C

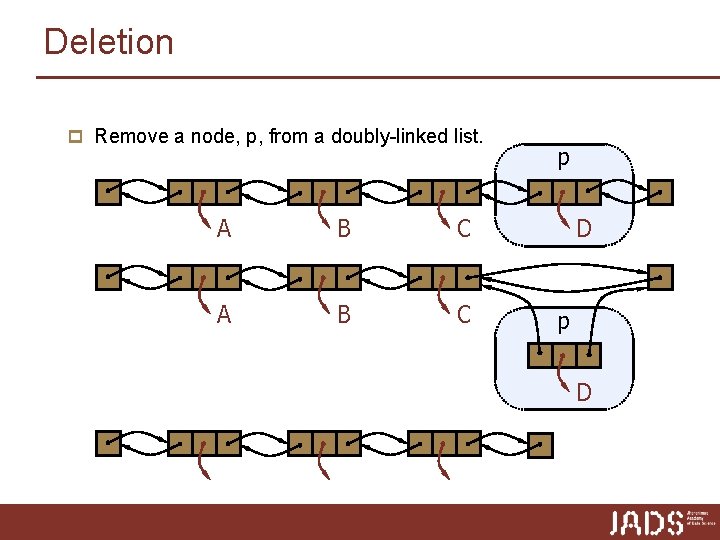
Deletion p Remove a node, p, from a doubly-linked list. A B C p D

Summary p ADTs we have seen so far n Stacks, Queues, (and Lists and Sets in Python) n next week: Dictionaries (data structure: hash table) p data structures for Stacks and Queues: n array, but fixed capacity n dynamic array n linked lists p Singly Linked Lists vs Doubly Linked Lists p amortized analysis: time required to perform a sequence of operations averaged over all the operations performed (T(n)/n)