Data Structures Algorithms Lecture 5 Data Structures Algorithms

Data Structures & Algorithms Lecture # 5

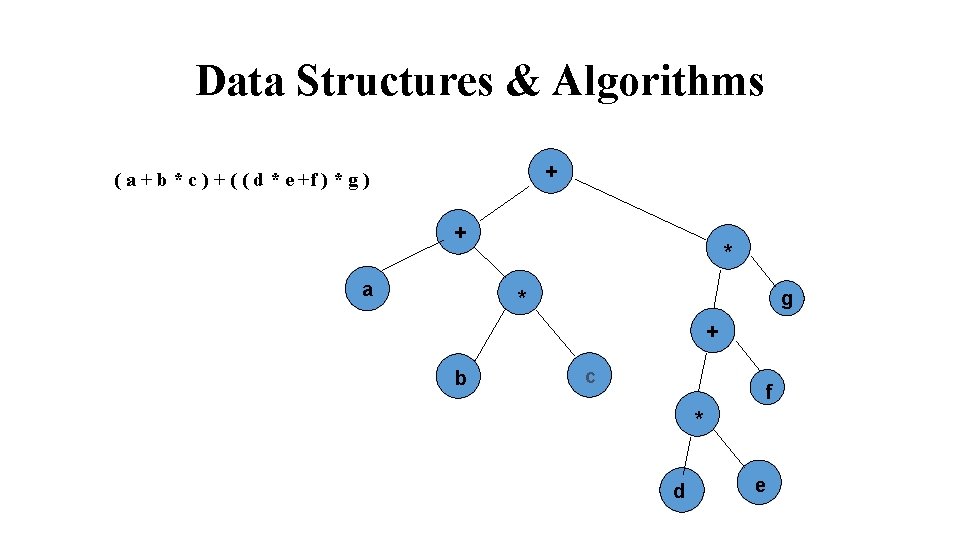
Data Structures & Algorithms Expression Tree: Expression Trees, and the more general parse tree and abstract syntax trees are significant components of compiler. Let us consider the expression tree.

Data Structures & Algorithms + ( a + b * c ) + ( ( d * e +f ) * g ) + a * g * + b c f * d e

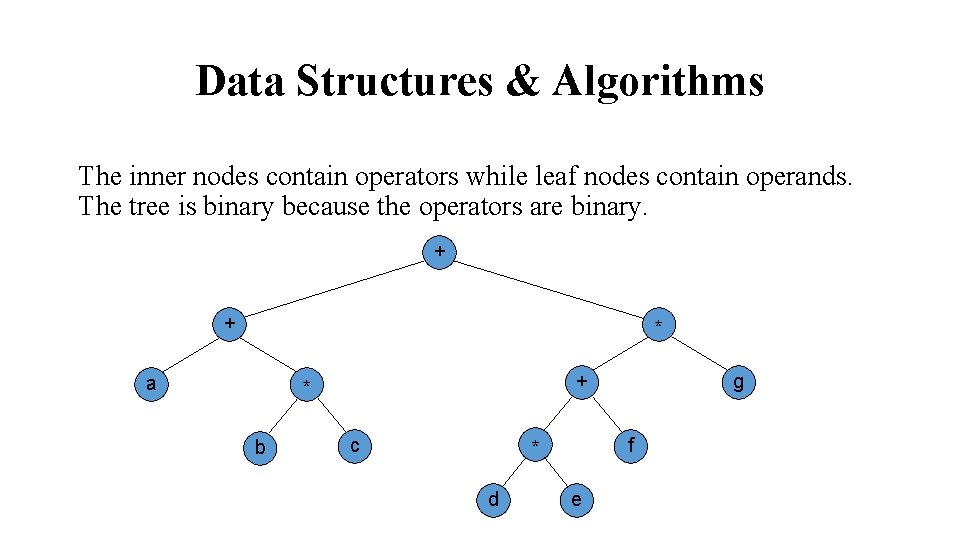
Data Structures & Algorithms The inner nodes contain operators while leaf nodes contain operands. The tree is binary because the operators are binary. + + * a + * b c f * d g e

Data Structures & Algorithms Inorder traversal yields: a+b*c+d*e+f*g + + * a + * b c f * d g e

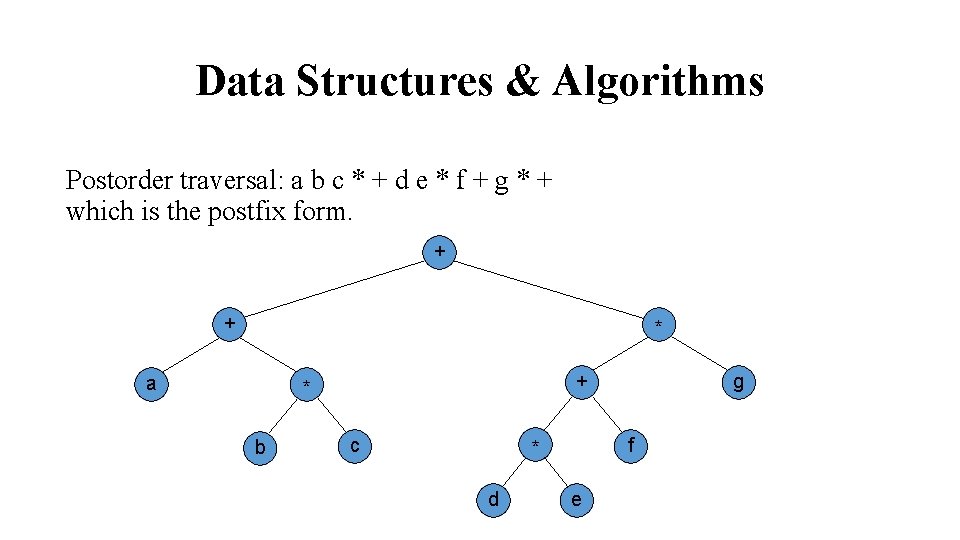
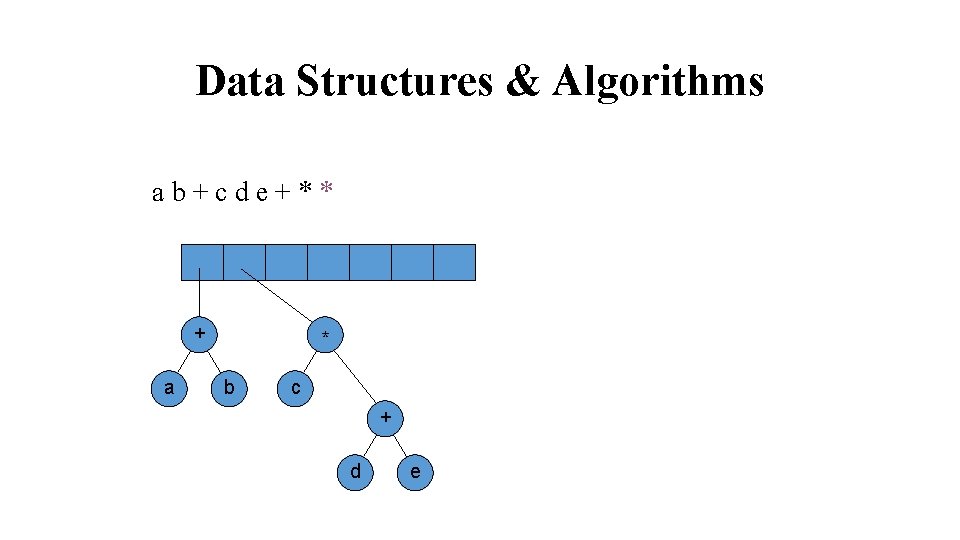
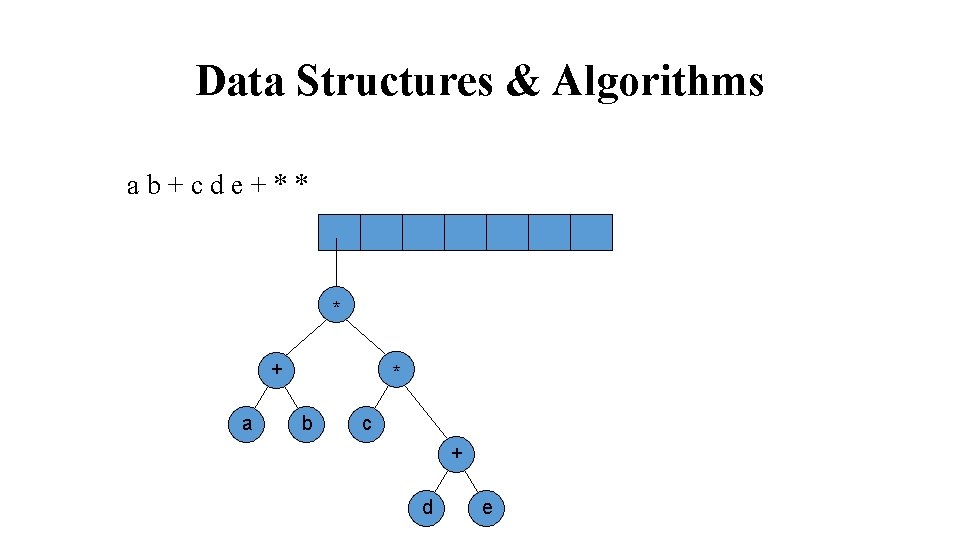
Data Structures & Algorithms Postorder traversal: a b c * + d e * f + g * + which is the postfix form. + + * a + * b c f * d g e

Data Structures & Algorithms Constructing Expression Tree ØAlgorithm to convert postfix expression into an expression tree. ØWe already have an expression to convert an infix expression to postfix. ØRead a symbol from the postfix expression. ØIf symbol is an operand, put it in a one node tree and push it on a stack. ØIf symbol is an operator, pop two trees from the stack, form a new tree with operator as the root and T 1 and T 2 as left and right subtrees and push this tree on the stack.

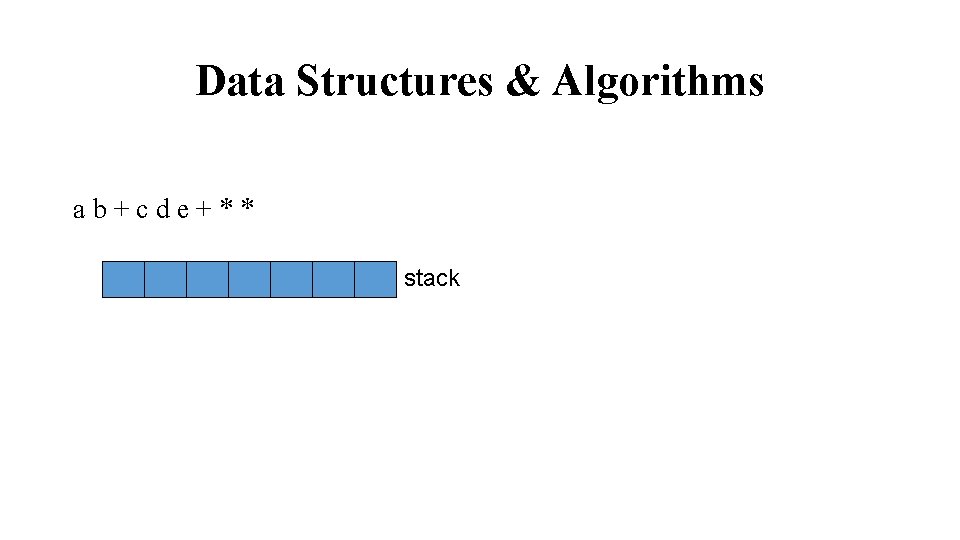
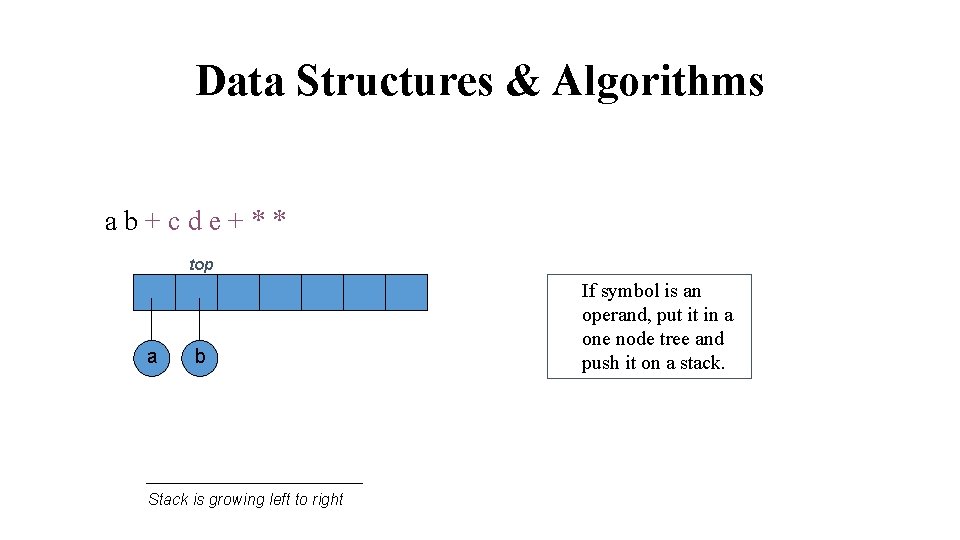
Data Structures & Algorithms ab+cde+** stack

Data Structures & Algorithms ab+cde+** top a b Stack is growing left to right If symbol is an operand, put it in a one node tree and push it on a stack.

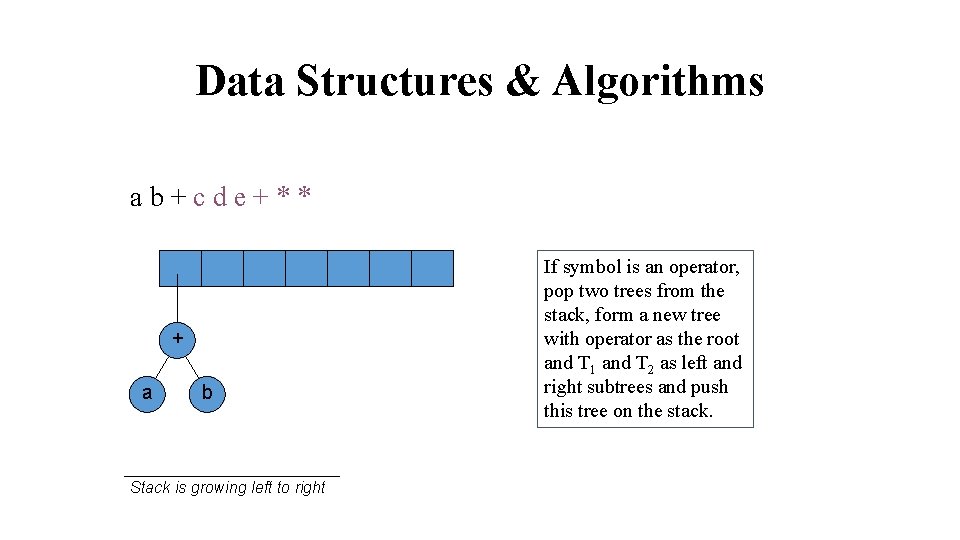
Data Structures & Algorithms ab+cde+** + a b Stack is growing left to right If symbol is an operator, pop two trees from the stack, form a new tree with operator as the root and T 1 and T 2 as left and right subtrees and push this tree on the stack.

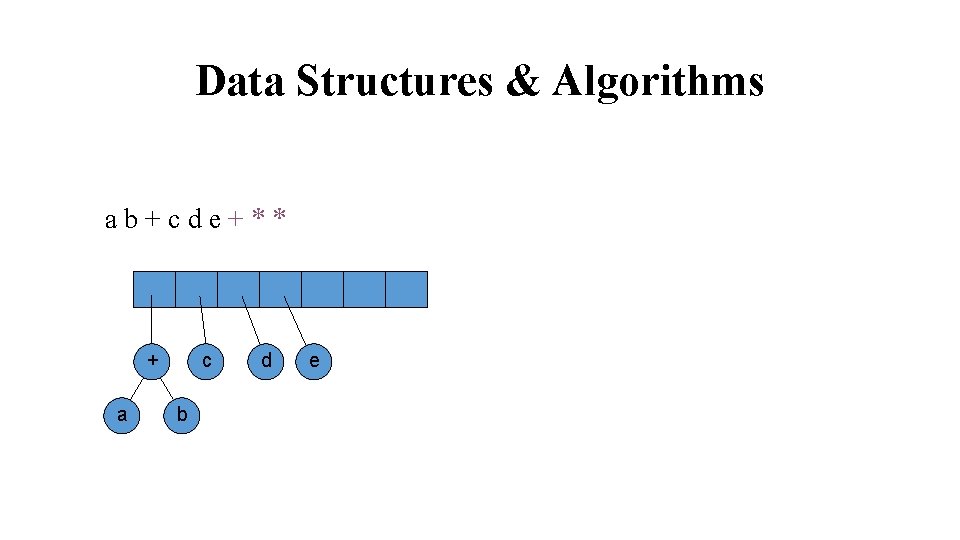
Data Structures & Algorithms ab+cde+** + a c b d e

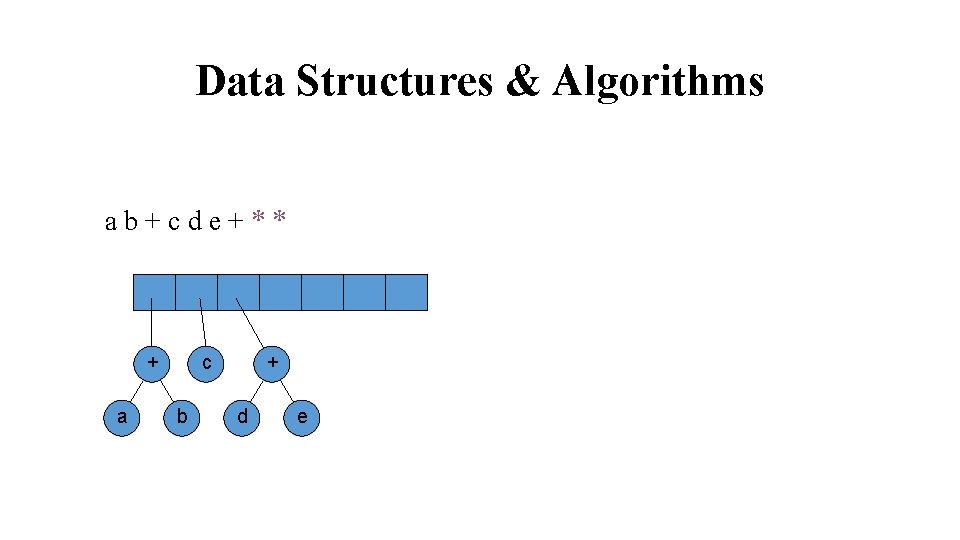
Data Structures & Algorithms ab+cde+** + a c b + d e

Data Structures & Algorithms ab+cde+** + a * b c + d e

Data Structures & Algorithms ab+cde+** * + a * b c + d e

Data Structures & Algorithms Other Uses of Binary Trees: Huffman Encoding Data compression plays a significant role in computer networks. To transmit data to its destination faster, it is necessary to either increase the data rate of the transmission media or to simply send less data. Improvements with regard to the transmission media has led to increase in the rate. The other options is to send less data by means of data compression. Compression methods are used for text, images, voice and other types of data (space probes).

Data Structures & Algorithms Huffman code is method for the compression for standard text documents. It makes use of a binary tree to develop codes of varying lengths for the letters used in the original message. Huffman code is also part of the JPEG image compression scheme. The algorithm was introduced by David Huffman in 1952 as part of a course assignment at MIT. To understand Huffman encoding, it is best to use a simple example.

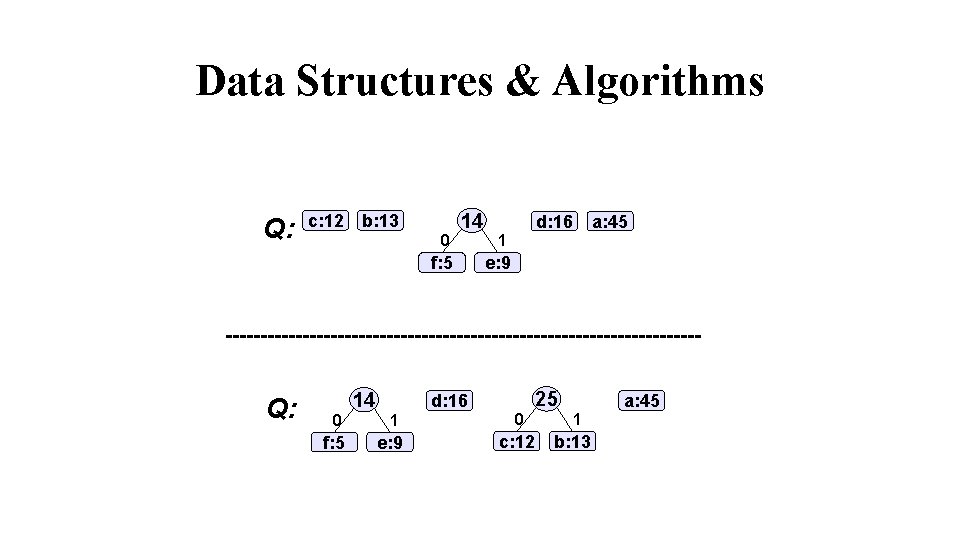
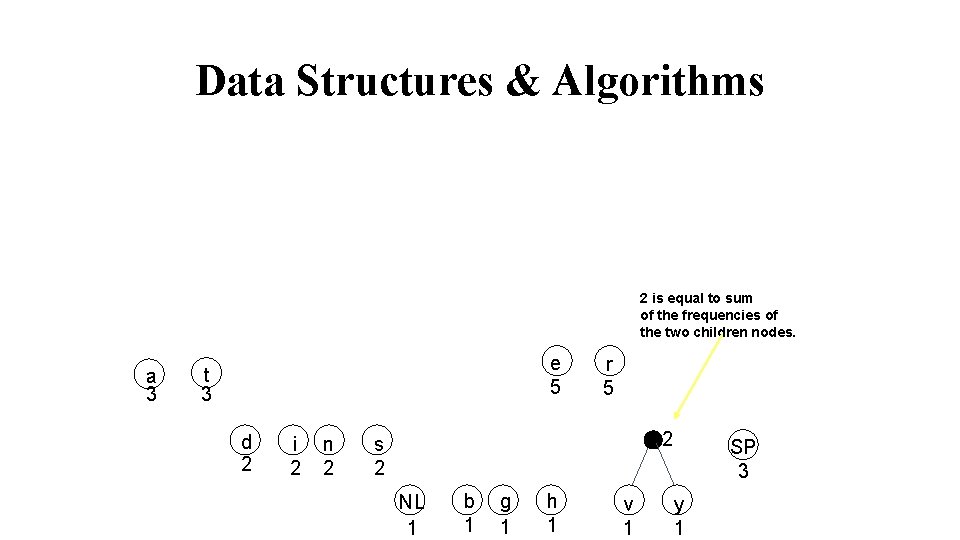
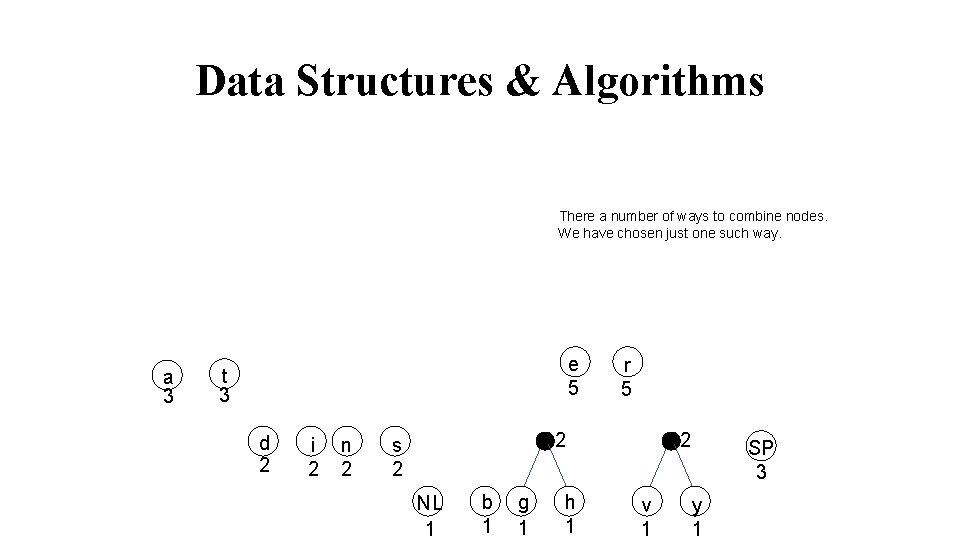
Data Structures & Algorithms List all the letters used, including the "space" character, along with the frequency with which they occur in the message. Consider each of these (character, frequency) pairs to be nodes; they are actually leaf nodes, as we will see. Pick the two nodes with the lowest frequency, and if there is a tie, pick randomly amongst those with equal frequencies. Make a new node out of these two, and make the two nodes its children. This new node is assigned the sum of the frequencies of its children. Continue the process of combining the two nodes of lowest frequency until only one node, the root, remains.

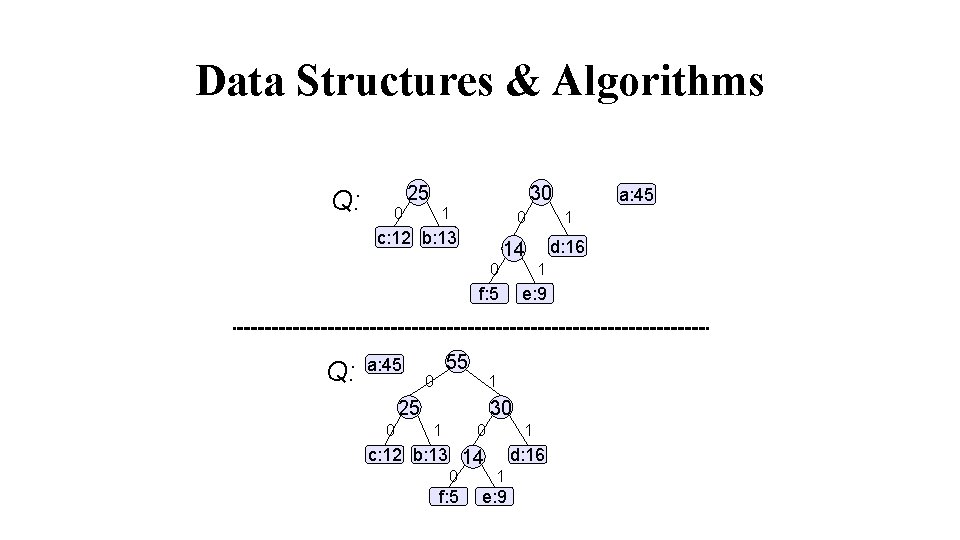
Data Structures & Algorithms Q: f: 5 e: 9 Q: c: 12 b: 13 14 0 1 f: 5 e: 9 d: 16 a: 45

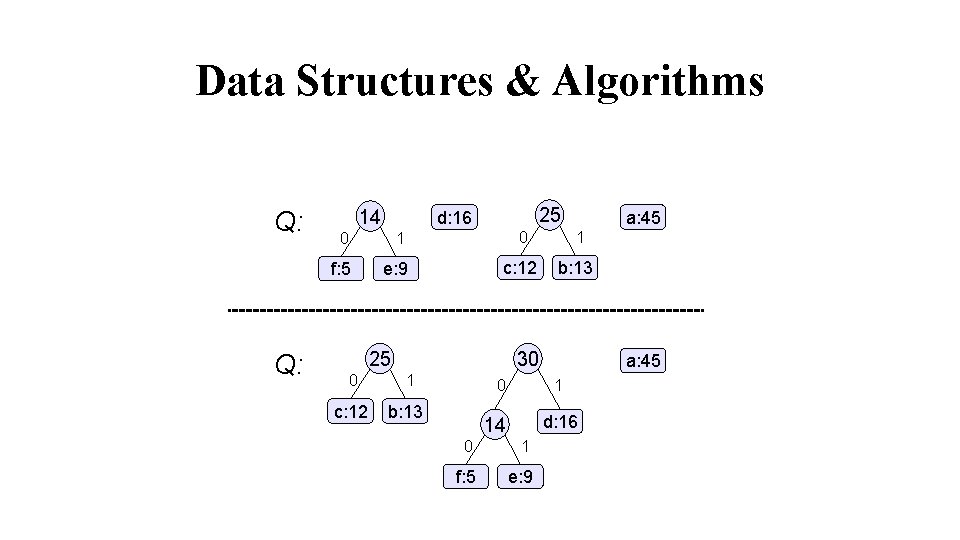
Data Structures & Algorithms Q: c: 12 b: 13 0 14 f: 5 Q: 0 f: 5 14 d: 16 1 e: 9 d: 16 a: 45 1 e: 9 0 c: 12 25 1 b: 13 a: 45

Data Structures & Algorithms Q: 14 25 d: 16 0 0 1 f: 5 e: 9 c: 12 25 0 c: 12 a: 45 1 b: 13 30 1 0 b: 13 a: 45 1 d: 16 14 0 1 f: 5 e: 9

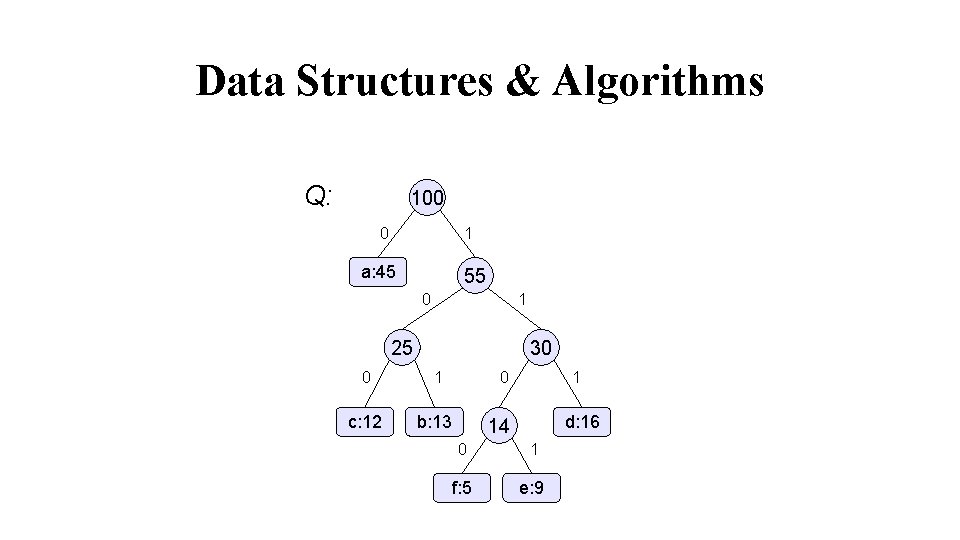
Data Structures & Algorithms Q: 25 30 0 1 0 c: 12 b: 13 Q: a: 45 0 d: 16 0 1 f: 5 e: 9 1 25 0 1 14 55 30 1 0 c: 12 b: 13 14 1 d: 16 0 1 f: 5 e: 9 a: 45

Data Structures & Algorithms Q: 100 0 1 a: 45 55 0 1 25 30 0 1 c: 12 b: 13 0 1 d: 16 14 0 1 f: 5 e: 9

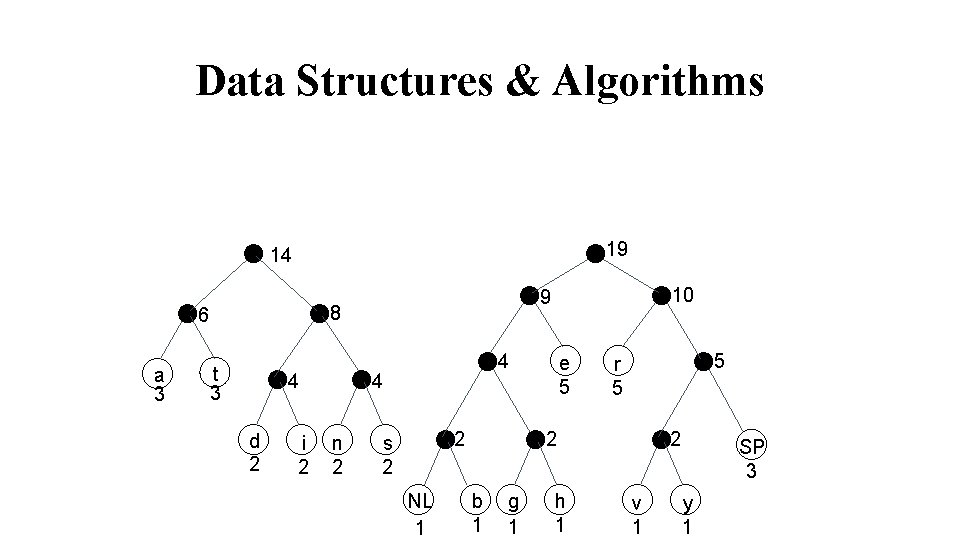
Data Structures & Algorithms Original text: traversing threaded binary trees size: 33 characters (space and newline) NL : 1 SP : 3 a: 3 b: 1 d: 2 e: 5 g: 1 h: 1 i: n: r: s: t: v: y: 2 2 5 2 3 1 1

Data Structures & Algorithms 2 is equal to sum of the frequencies of the two children nodes. a 3 e 5 t 3 d 2 i 2 n 2 r 5 2 s 2 NL 1 b 1 g 1 h 1 v 1 SP 3 y 1

Data Structures & Algorithms There a number of ways to combine nodes. We have chosen just one such way. a 3 e 5 t 3 d 2 i 2 n 2 r 5 2 s 2 NL 1 b 1 g 1 h 1 2 v 1 SP 3 y 1

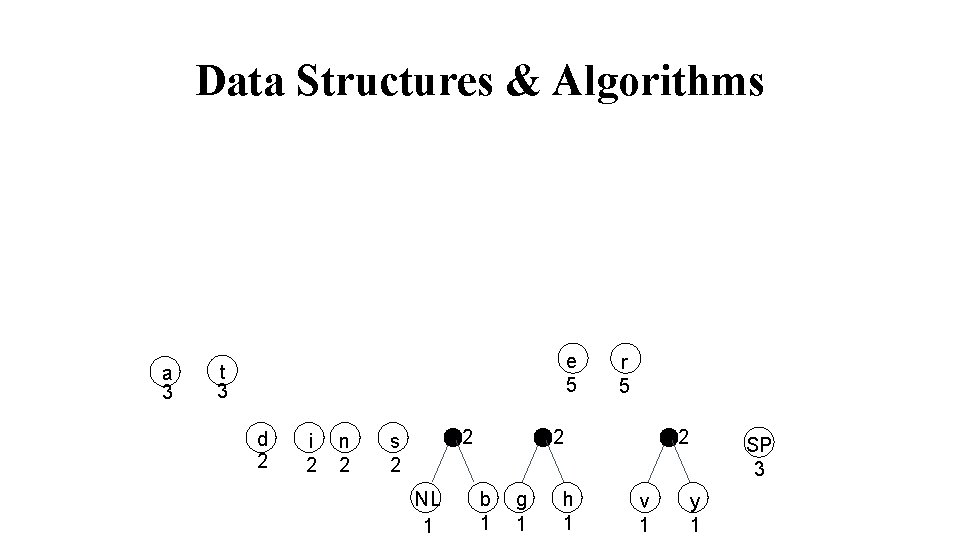
Data Structures & Algorithms a 3 e 5 t 3 d 2 i 2 n 2 2 s 2 NL 1 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

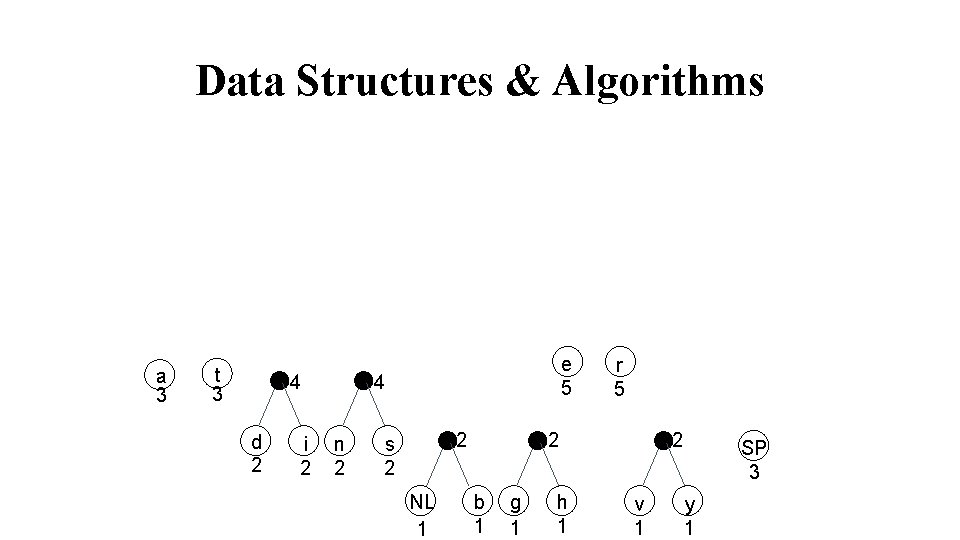
Data Structures & Algorithms a 3 t 3 4 d 2 i 2 e 5 4 n 2 2 s 2 NL 1 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

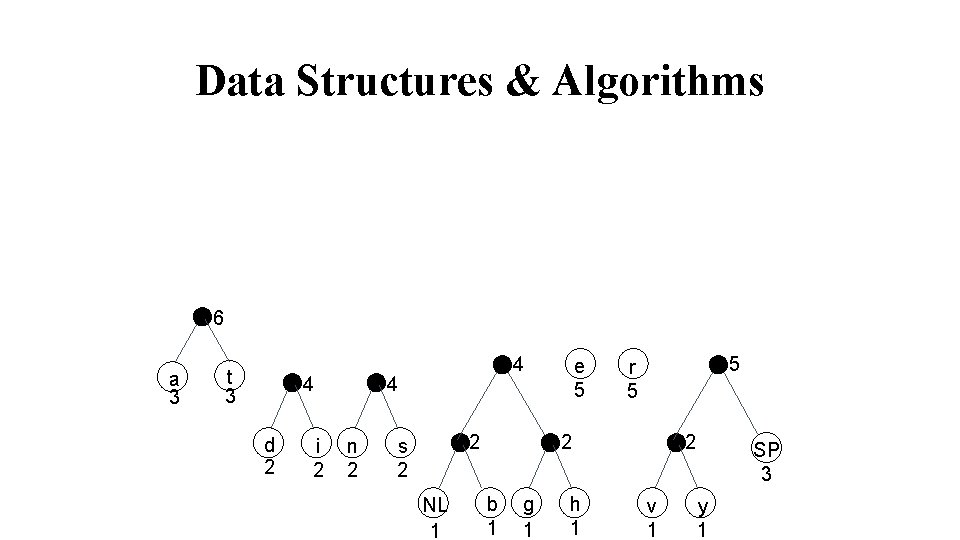
Data Structures & Algorithms 6 a 3 t 3 4 d 2 i 2 4 4 n 2 2 s 2 NL 1 e 5 5 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

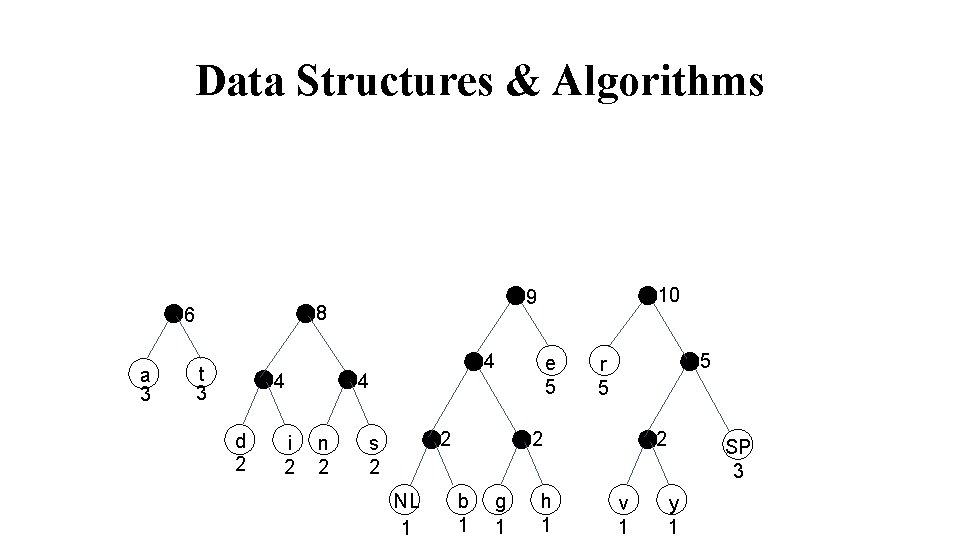
Data Structures & Algorithms 8 6 a 3 t 3 4 d 2 i 2 4 4 n 2 10 9 2 s 2 NL 1 e 5 5 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

Data Structures & Algorithms 19 14 8 6 a 3 t 3 4 d 2 i 2 4 4 n 2 10 9 2 s 2 NL 1 e 5 5 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

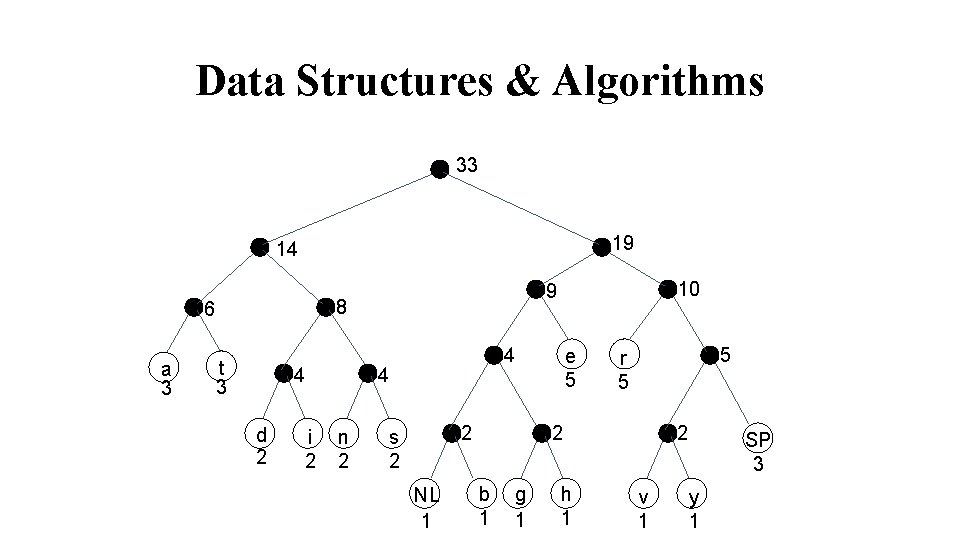
Data Structures & Algorithms 33 19 14 8 6 a 3 t 3 4 d 2 i 2 4 4 n 2 10 9 2 s 2 NL 1 e 5 5 r 5 2 b 1 g 1 h 1 2 v 1 SP 3 y 1

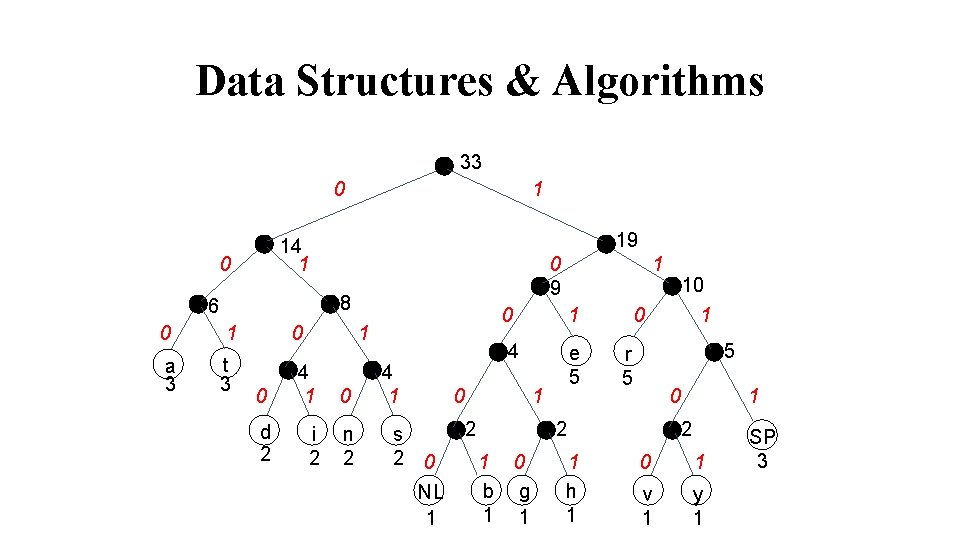
Data Structures & Algorithms Start at the root. Assign 0 to left branch and 1 to the right branch. Repeat the process down the left and right subtrees. To get the code for a character, traverse the tree from the root to the character leaf node and read off the 0 and 1 along the path.

Data Structures & Algorithms 33 0 1 19 14 1 0 0 9 8 6 0 1 a 3 t 3 0 4 1 d 2 i 2 n 2 s 2 0 1 4 e 5 0 1 2 0 NL 1 1 0 5 r 5 0 2 1 b 1 0 g 1 1 h 1 10 1 1 2 0 1 v 1 y 1 SP 3

Data Structures & Algorithms Huffman character codes NL SP a b d e g h i n r s t v y 10000 1111 000 10001 0100 101 10010 10011 0101 0110 0111 001 11100 11101 • Notice that the code is variable length. • Letters with higher frequencies have shorter codes. • The tree could have been built in a number of ways; each would yielded different codes but the code would still be minimal.

Data Structures & Algorithms Original: traversing threaded binary trees Encoded: 00111001011101010110100101111001 t r a v e 10011110101000010010101001111100001010110000 11011111001110101110000

Data Structures & Algorithms Original: traversing threaded binary trees With 8 bits per character, length is 264. Encoded: 001110010111010101101001011110011110101000010010101001111100001010110000 11011111001110101110000 Compressed into 122 bits, 54% reduction.

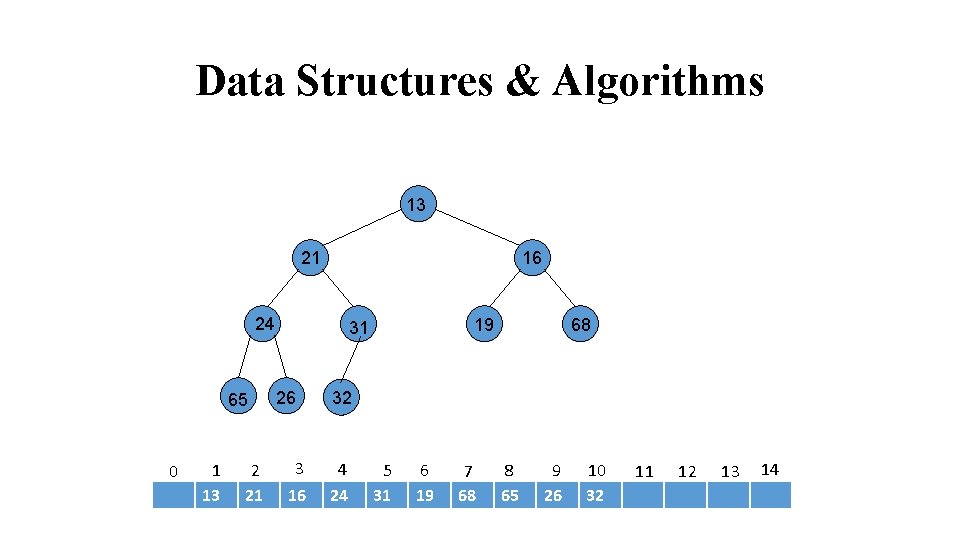
Data Structures & Algorithms Heap Tree: A Heap Tree is a left-complete binary tree that conforms to the heap order. The Heap order property: 1) In min heap, for every node X, the key in the parent is smaller or equal to X. In other word the parent node has smaller value than or equal to both of its children's. 2) Similarly, in a max heap, the parent has a value larger than or equal to both of its children's. Thus smallest key is in the root in case of min heap, and largest key is in the root in case of max heap

Data Structures & Algorithms 13 21 16 24 65 0 1 13 2 21 19 31 26 3 16 68 32 4 24 5 31 6 19 7 68 8 65 9 26 10 32 11 12 13 14

Data Structures & Algorithms Heap Sort Algorithm: ØWe build a max heap out of the given array of numbers A[1. . . n]. ØWe repeatedly extract the maximum item from the heap. ØOnce the max item is removed, we are left with a hole at the root. ØTo fix this, we will replace it with the last leaf in tree.

Data Structures & Algorithms 1. 2. 3. 4. 5. 6. Heapsort(array A, int n) Build_Heap(A, n) O(nlogn) m=n While(m≥ 2) do swap A[1] and A[m] O(n) m=m-1 Heapify(A, 1, m) O(logn) Heapify(array A, int i, int n) I = left(i) R= right(i) Max=i If (I≤m) and (A[I]>A[max]) Then max= I If (R ≤m) and (A[R]>A[max]) Then max= R If (max!=i) { Then swap (A[i] and A[max]) Heapify (A, max, m) }

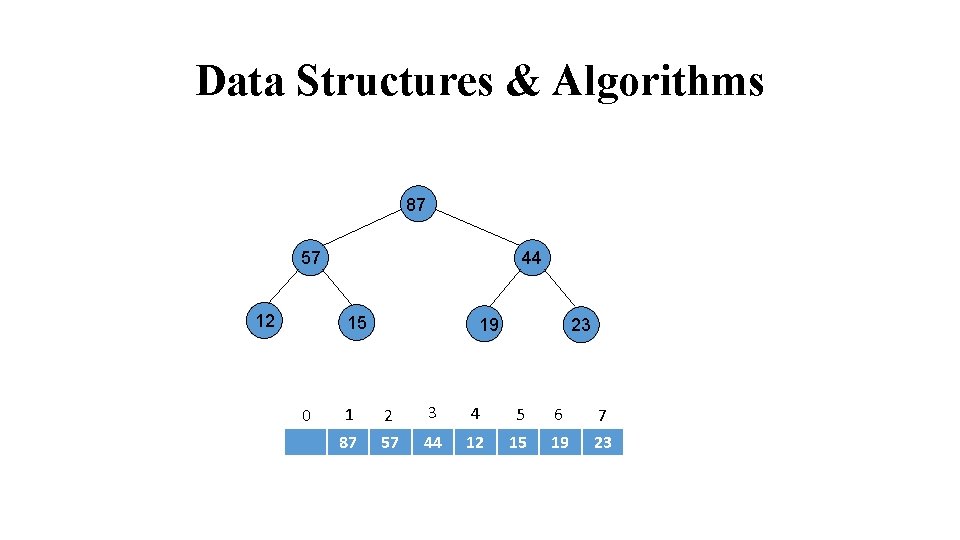
Data Structures & Algorithms 87 57 12 24 44 15 31 0 19 23 68 1 2 3 4 5 6 7 87 57 44 12 15 19 23

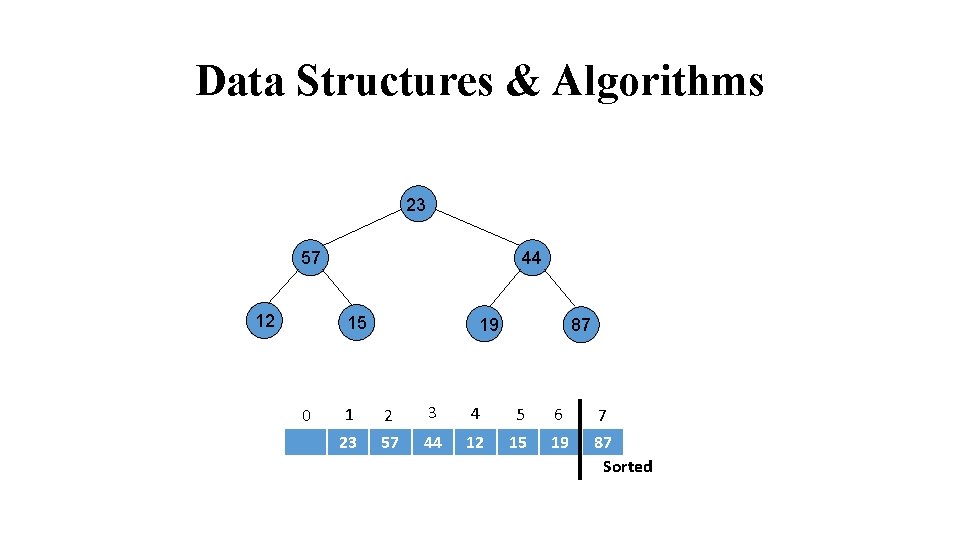
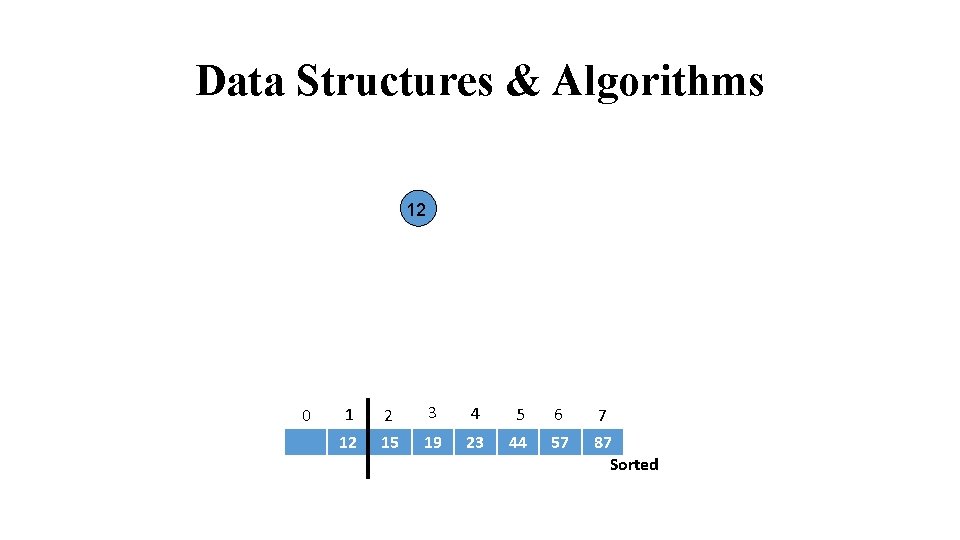
Data Structures & Algorithms 23 57 12 24 44 15 31 0 19 87 68 1 2 3 4 5 6 7 23 57 44 12 15 19 87 Sorted

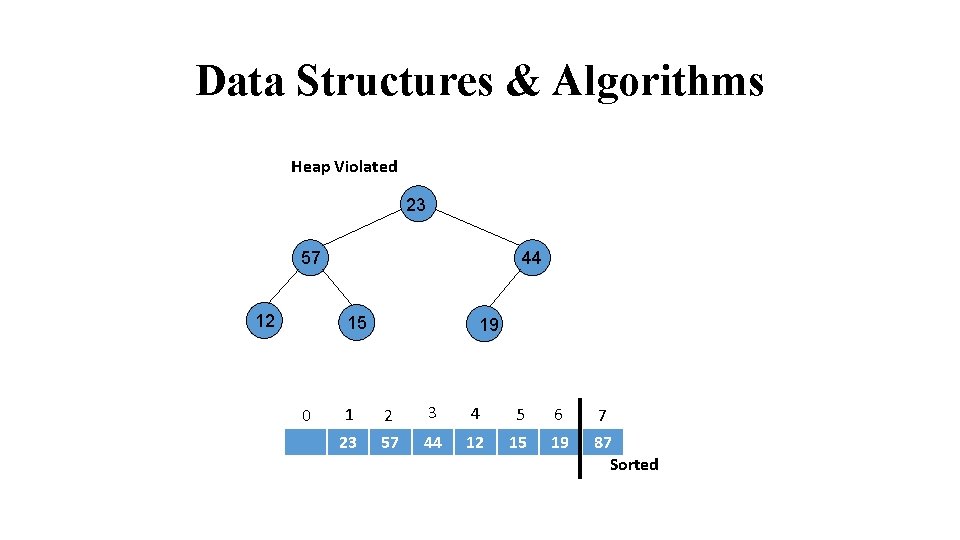
Data Structures & Algorithms Heap Violated 23 57 12 24 44 15 31 0 19 1 2 3 4 5 6 7 23 57 44 12 15 19 87 Sorted

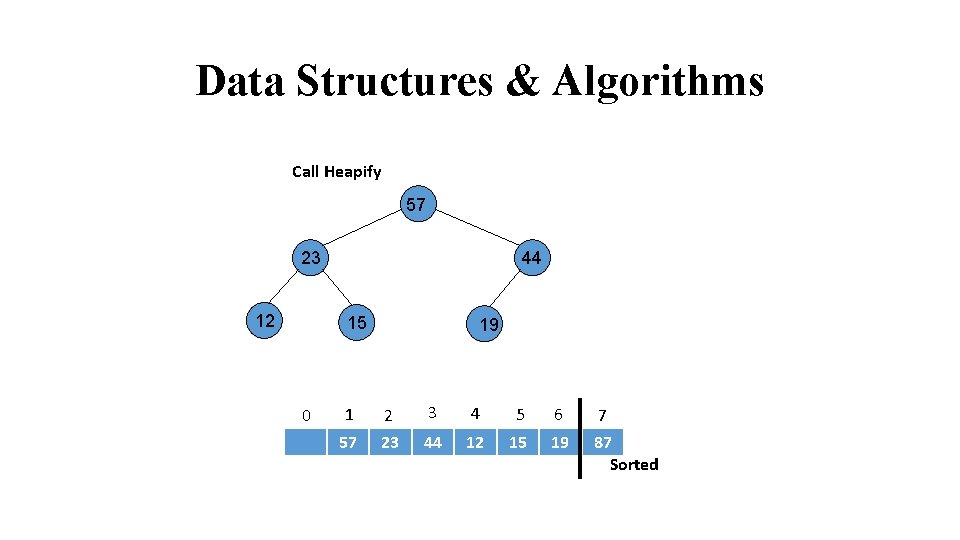
Data Structures & Algorithms Call Heapify 57 23 12 24 44 15 31 0 19 1 2 3 4 5 6 7 57 23 44 12 15 19 87 Sorted

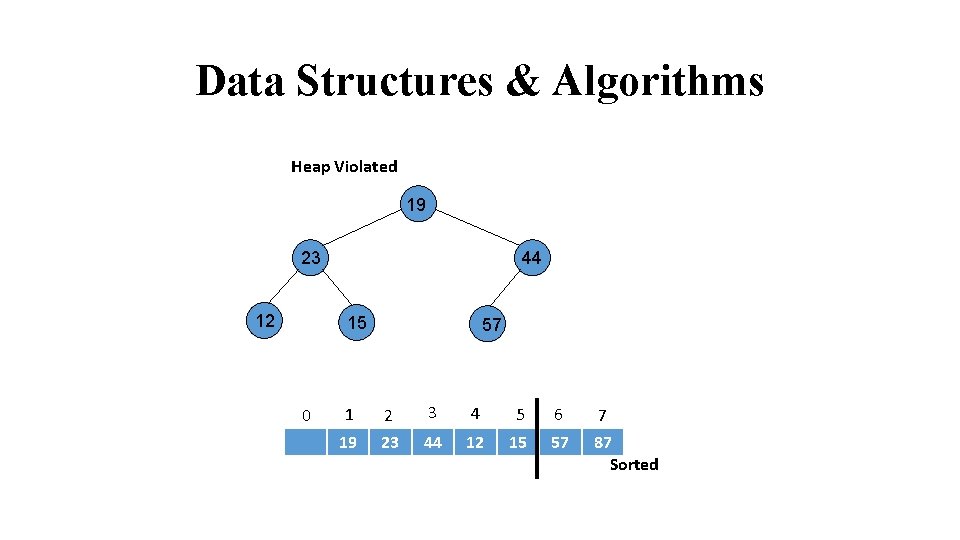
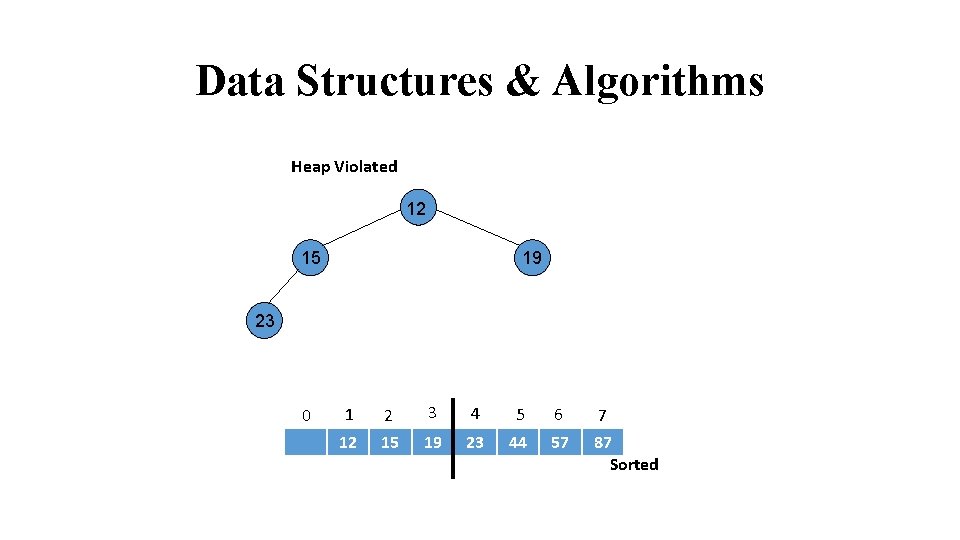
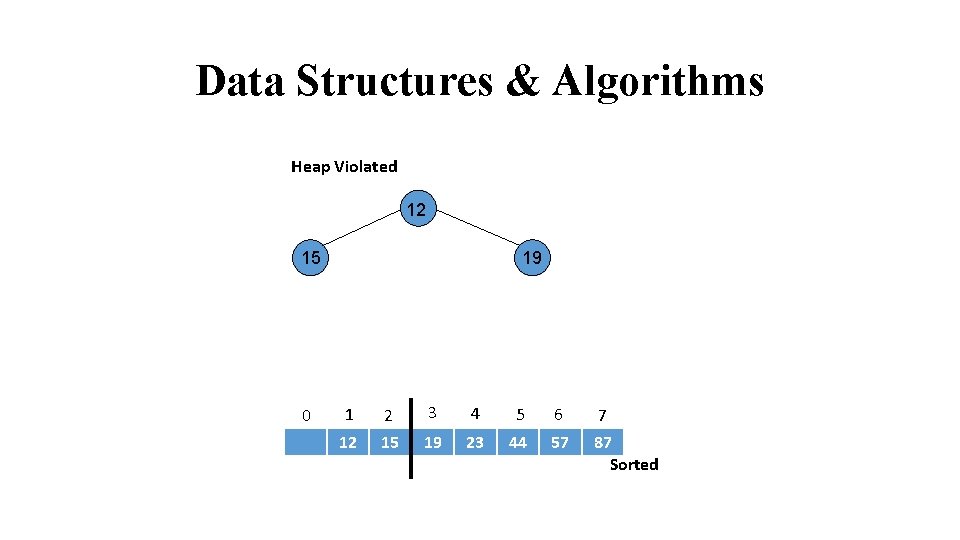
Data Structures & Algorithms Heap Violated 19 23 12 24 44 15 31 0 57 1 2 3 4 5 6 7 19 23 44 12 15 57 87 Sorted

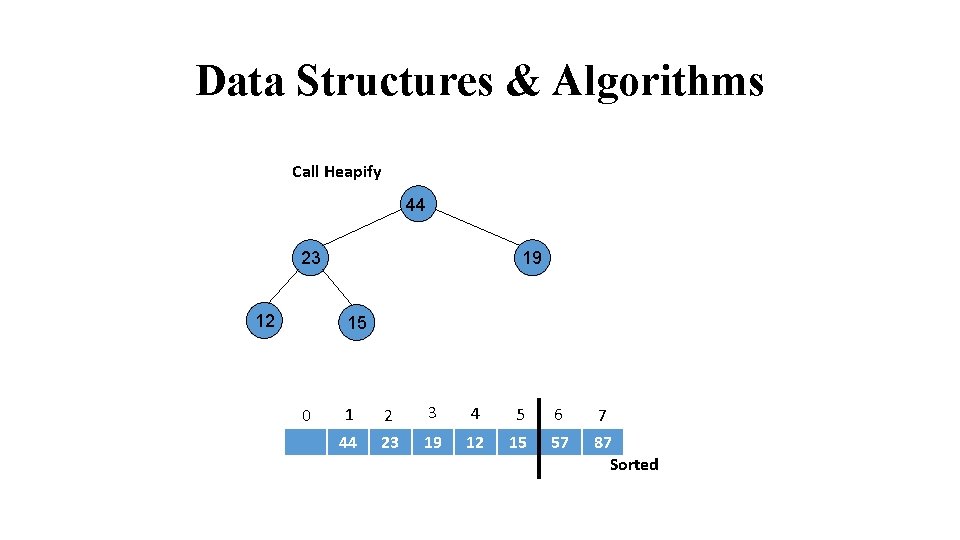
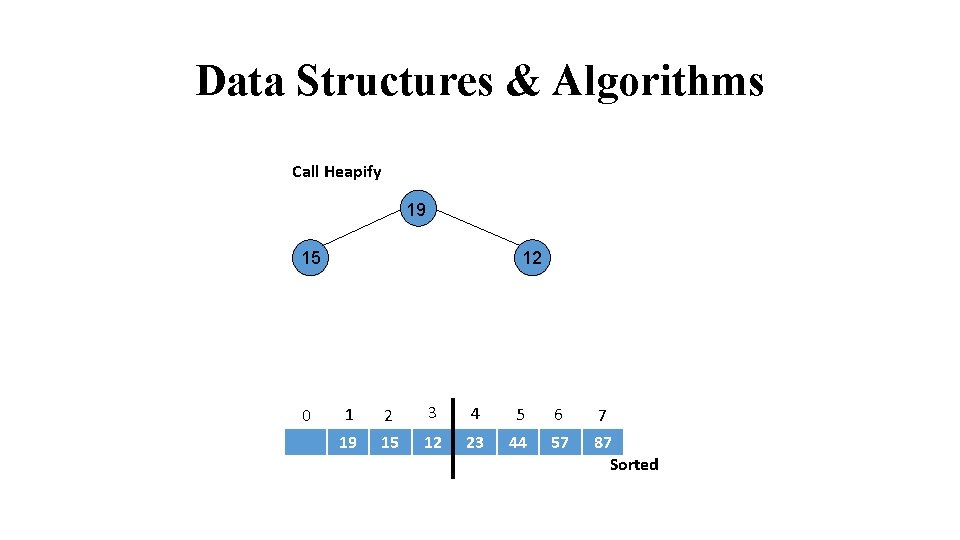
Data Structures & Algorithms Call Heapify 44 23 12 24 19 15 31 0 1 2 3 4 5 6 7 44 23 19 12 15 57 87 Sorted

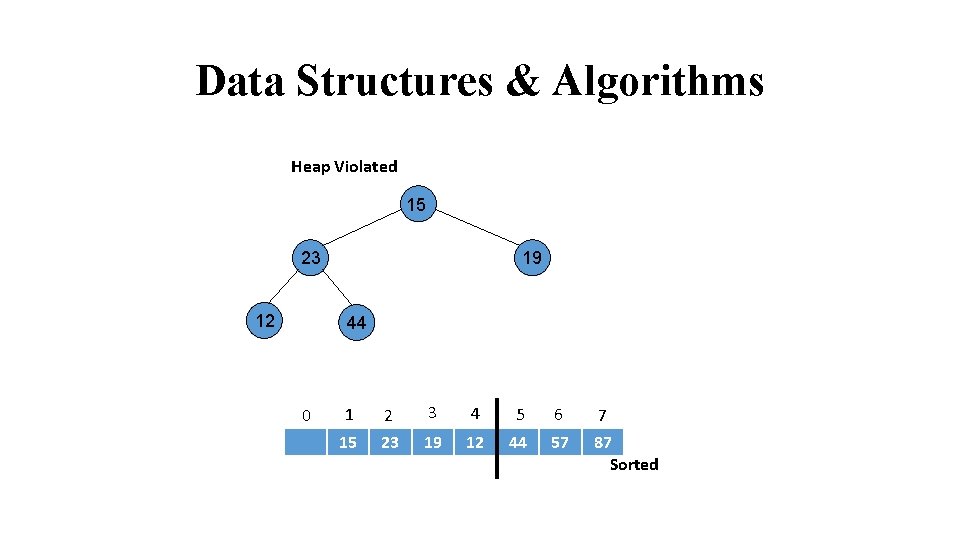
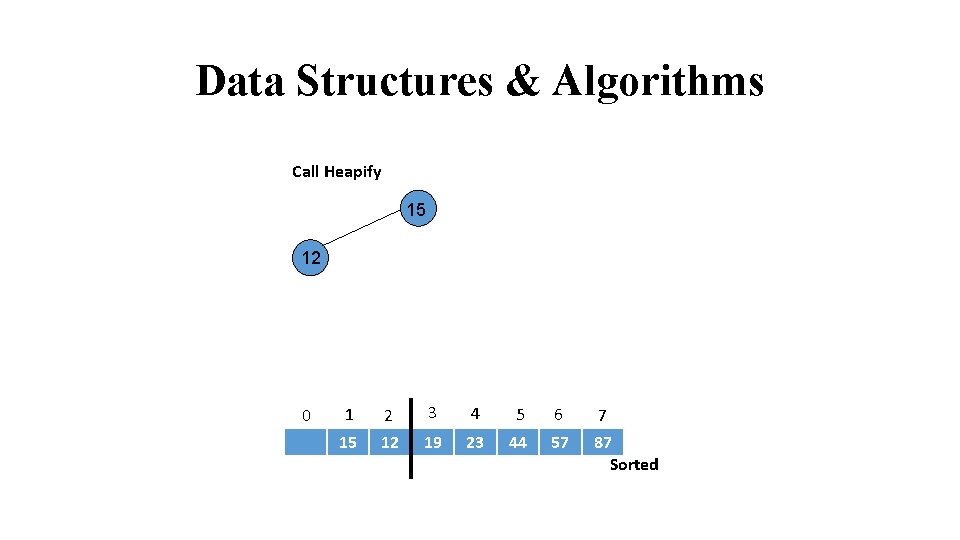
Data Structures & Algorithms Heap Violated 15 23 12 24 19 44 31 0 1 2 3 4 5 6 7 15 23 19 12 44 57 87 Sorted

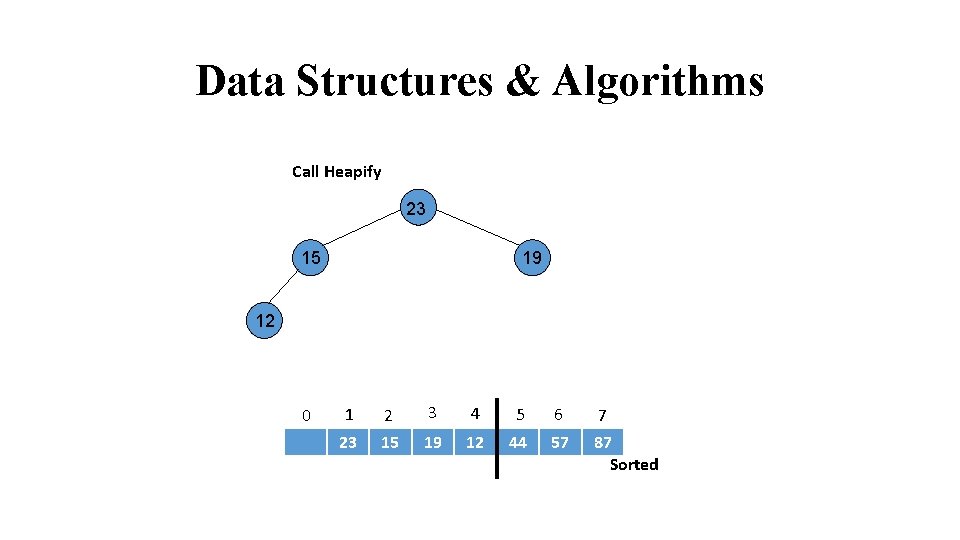
Data Structures & Algorithms Call Heapify 23 15 19 12 24 0 1 2 3 4 5 6 7 23 15 19 12 44 57 87 Sorted

Data Structures & Algorithms Heap Violated 12 15 19 23 24 0 1 2 3 4 5 6 7 12 15 19 23 44 57 87 Sorted

Data Structures & Algorithms Call Heapify 19 15 0 12 1 2 3 4 5 6 7 19 15 12 23 44 57 87 Sorted

Data Structures & Algorithms Heap Violated 12 15 0 19 1 2 3 4 5 6 7 12 15 19 23 44 57 87 Sorted

Data Structures & Algorithms Call Heapify 15 12 0 1 2 3 4 5 6 7 15 12 19 23 44 57 87 Sorted

Data Structures & Algorithms 12 0 1 2 3 4 5 6 7 12 15 19 23 44 57 87 Sorted

Data Structures & Algorithms Analysis of Heapify: ØWe call heapify on the root of the tree. ØThe maximum levels the element could move is logn levels. ØAt each level we do simple comparison, which takes O(1). ØThus the total time for heapify is O(logn) ØNotice that it is not (logn)

Data Structures & Algorithms ØIt traces a path from the root to a leaf (longest path : d) ØAt each level, it make exactly 2 comparisons. Ø Total number of comparisons is 2 d. Running time is O(d) or O(Logn). ØRunning time of MAX-HEAPIFY is O(lgn) ØCan be written in terms of the height of the heap, as being O(h) ØSince the height of the heap is lgn

Data Structures & Algorithms BUILDHEAP(Array a, int n) For i=n/2 down to 1 do HEAPIFY(A, i, n) O(lgn) Running Time= O(nlogn) O(n) Heapify(array A, int i, int n) I = left(i) R= right(i) Max=i If (I≤m) and (A[I]>A[max]) Then max= I If (R ≤m) and (A[R]>A[max]) Then max= R If (max!=i) { Then swap (A[i] and A[max]) Heapify (A, max, m) }

Data Structures & Algorithms ØHeap call Build heap once this take O(nlogn). ØHeapsort then extract “n” maximum elements from the heap. ØEach extract require a constant amount of work (swap), and logn heapify. ØHeapsort is thus O(nlogn + nlogn) => O(2 nlogn) => O(nlogn) ØIs Heapsort is (nlogn). ØThe answer is yes. ØIn fact, later we will show that comparisons based sorting algorithms can not run faster than Ω(nlogn).