Data Structures Algorithm 2 nd Week Chapter 1

Data Structures & Algorithm 2 nd Week Chapter 1. Basic Concepts 1. 1 Overview: System Life Cycle 1. 2 Algorithm Specification 1. 3 Data Abstraction 1. 4 Performance Analysis – space and time complexity

Chapter 1 Basic Concepts

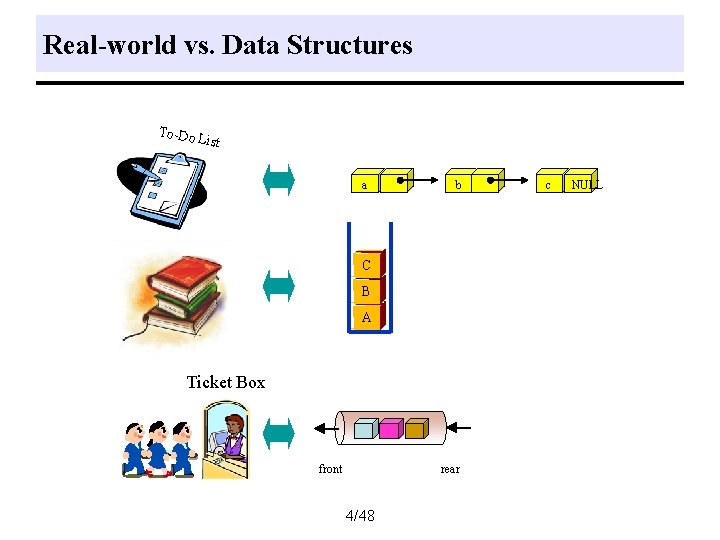
Data Structures To-Do Organization chart List In the Real-world Dictionary Ticket Box 3/48

Real-world vs. Data Structures To-Do List a b C B A Ticket Box front rear 4/48 c NULL

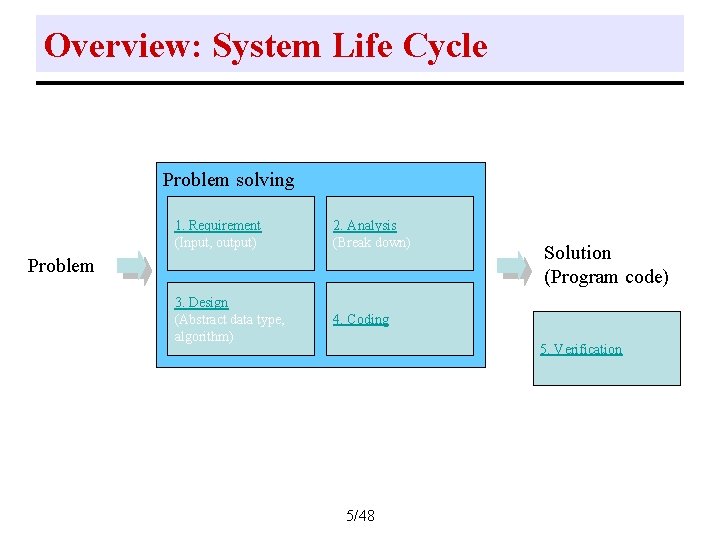
Overview: System Life Cycle Problem solving 1. Requirement (Input, output) 2. Analysis (Break down) 3. Design (Abstract data type, algorithm) 4. Coding Problem Solution (Program code) 5. Verification 5/48

Requirements q Define purpose/goal of system – Define input, output of system • Covers all cases • Definite/detailed description q Input – The information that we are given q Output – The results that we must produce input System 6/48 output

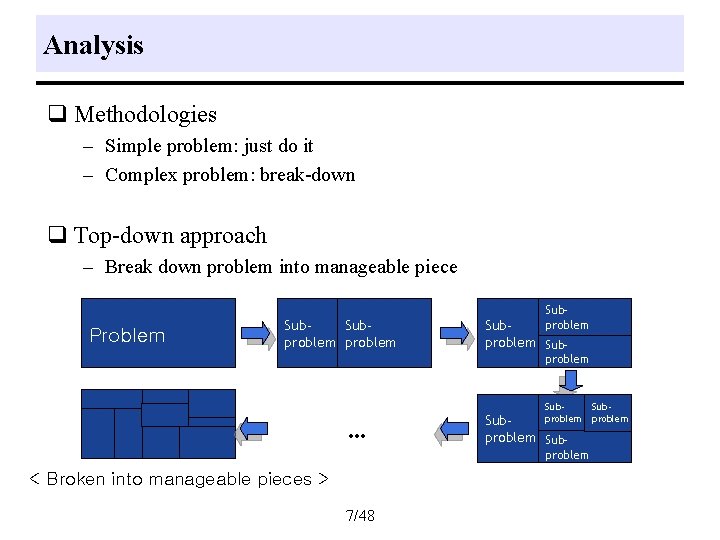
Analysis q Methodologies – Simple problem: just do it – Complex problem: break-down q Top-down approach – Break down problem into manageable piece Problem Subproblem Sub- problem … Subproblem Sub- problem < Broken into manageable pieces > 7/48

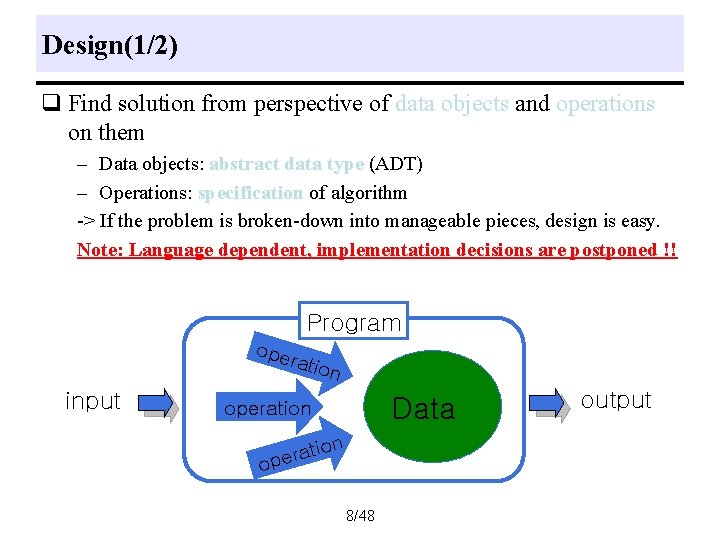
Design(1/2) q Find solution from perspective of data objects and operations on them – Data objects: abstract data type (ADT) – Operations: specification of algorithm -> If the problem is broken-down into manageable pieces, design is easy. Note: Language dependent, implementation decisions are postponed !! Program ope ratio n input Data operation n tio a r e op 8/48 output

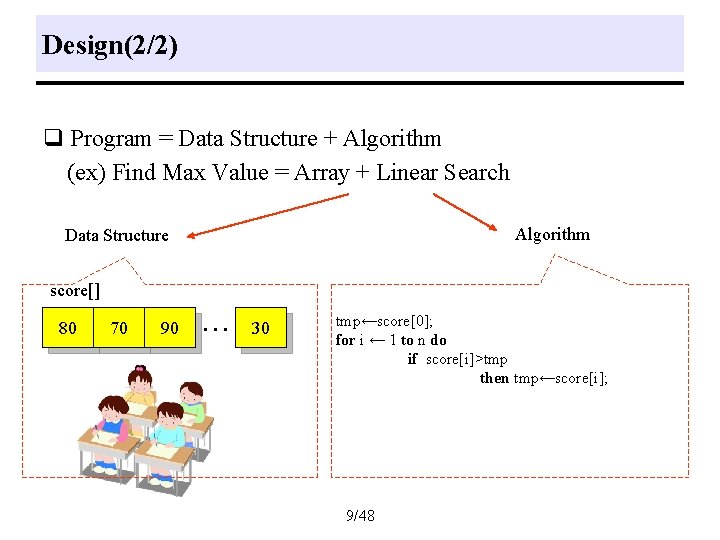
Design(2/2) q Program = Data Structure + Algorithm (ex) Find Max Value = Array + Linear Search Algorithm Data Structure score[] 80 70 90 … 30 tmp←score[0]; for i ← 1 to n do if score[i]>tmp then tmp←score[i]; 9/48

Refinement and coding q Choose representations for the data objects and write algorithms for each operation q The order is crucial – A data object’s representation can determine the efficiency of the algorithms related to it 10/48

Verification q Correctness proofs – Selecting algorithms that have been proven correct can reduce the number of errors q Testing – Error-free program – Requires working code and sets of test data q Error removal – The ease of error removal depends on the design and coding decisions – Well-documented and modularized programming 11/48

Algorithm specification q Definition: a finite set of instruction that accomplishes a particular task – – Input: zero or more quantities Output: at least one quantity Definiteness: clear and unambiguous instructions Finiteness: for all cases, algorithm terminates after finite step • Difference from program – Effectiveness: basic and feasible instructions q Description of an algorithm – Natural language, flowchart, Pseudo-code, C-style code 12/48

Algorithm description by natural language q Natural language – Easy to read – However, if the words in the natural language are not defined correctly, there is a concern that the meaning transmission becomes ambiguous (ex) Algorithm to find max value in arrays Array. Max(A, n) 1. Copy first element of array A to variable tmp 2. Compare next elements sequentially with tmp. If element larger than tmp, copy element to tmp 3. If all comparison is done, return tmp 13/48

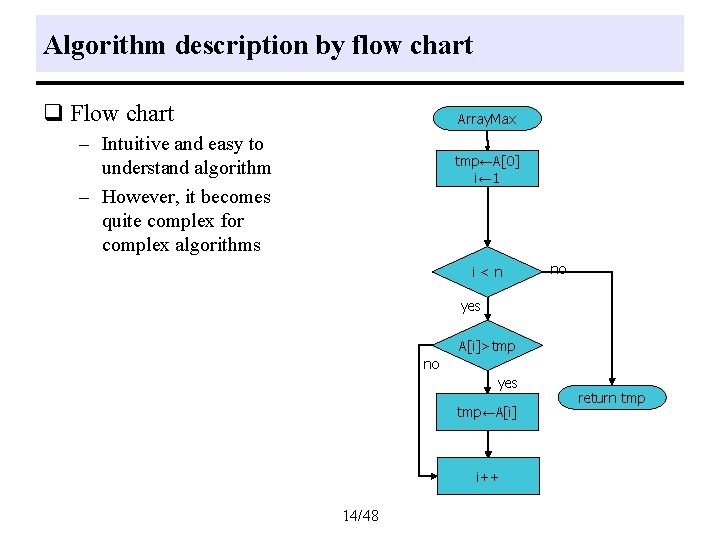
Algorithm description by flow chart q Flow chart Array. Max – Intuitive and easy to understand algorithm – However, it becomes quite complex for complex algorithms tmp←A[0] i← 1 i<n no yes A[i]>tmp no yes tmp←A[i] i++ 14/48 return tmp

Algorithm description by pseudo code q Pseudo Code – High-level description method of algorithm – More structured representation than natural language – A less specific representation than a programming language – Most used in algorithm description – It is possible to hide various problems when implementing a program. – In other words, we can concentrate on the core contents of the algorithm 15/48 Array. Max(A, n) tmp ← A[0]; for i← 1 to n-1 do if tmp < A[i] then tmp ← A[i]; return tmp; Assignment operator

Algorithm description by programming language q Programming Language – The most accurate description of the algorithm is possible – On the other hand, in actual implementation, many specifics may interfere with understanding the core contents of the algorithm. #define MAX_ELEMENTS 100 int score[MAX_ELEMENTS]; int find_max_score(int n) { int i, tmp; tmp=score[0]; for(i=1; i<n; i++){ if( score[i] > tmp ){ tmp = score[i]; } } return tmp; } 16/48

(ex) Selection sort q Sorts a set of n≥ 1 integers – From those integers that are currently unsorted, find the smallest and place it next the sorted list • Not tell us where and how the integers are initially sorted, or where we should place the result for(i=0; i<n-1; i++) { Examine list[i] to list[n-1] and suppose that the smallest integer is at list[min]; Interchange list[i] and list[min]; } 17/48

(ex) Selection sort q Problem definition: sort n integers list[0] list[1] list[2] list[3] list[4] 6 5 3 4 2 step 0 2 5 3 4 6 step 1 2 3 5 4 6 step 2 18/48 2 3 4 5 6 step 3 2 3 4 5 6 step 4 sorted unsorted

Selection sort source #include <stdio. h> #include <math. h> #define MAX_SIZE 101 #define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t)) void sort(int[], int); /* selection sort */ void main(void) { int i, n; int list[MAX_SIZE]; printf(“Enter the number of numbers to generate: ”); scanf(“%d”, &n); if(n < 1 || n > MAX_SIZE) { fprintf(stderr, “Improper value of nn”); exit(1); } for(i = 0; i < n; i++) { /* randomly generate numbers */ list[i] = rand() % 1000; printf(“%d”, list[i]); } 19/48

Selection sort source (cont’d) sort(list, n); printf(“n Sorted array: n”); for(i = 0; i < n; i++) printf(“%d”, list[i]); printf(“n”); /* print out sorted numbers */ } void sort(int list[], int n) { int i, j, min, temp; for(i = 0; i < n-1; i++) { min = i; for(j = i+1; j < n; j++) if(list[j] < list[min]) min = j; SWAP(list[i], list[min], temp); } } 20/48

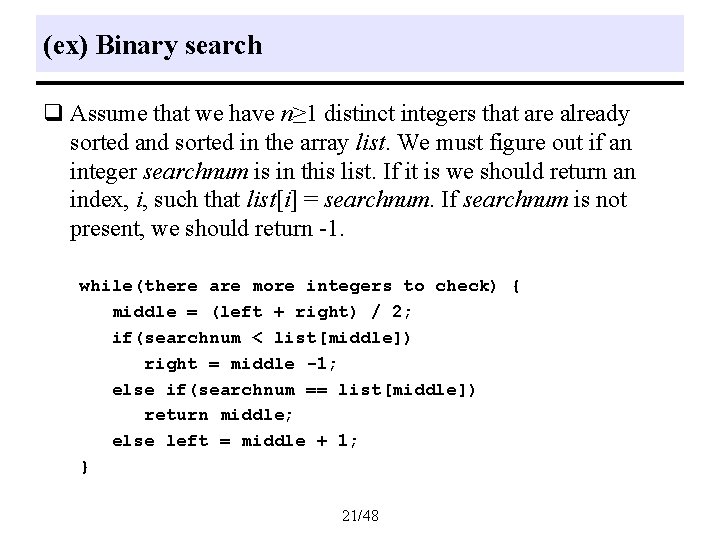
(ex) Binary search q Assume that we have n≥ 1 distinct integers that are already sorted and sorted in the array list. We must figure out if an integer searchnum is in this list. If it is we should return an index, i, such that list[i] = searchnum. If searchnum is not present, we should return -1. while(there are more integers to check) { middle = (left + right) / 2; if(searchnum < list[middle]) right = middle -1; else if(searchnum == list[middle]) return middle; else left = middle + 1; } 21/48

(ex) Searching an ordered list int binsearch(int list[], int searchnum, int left, int right) { /* search list[0] <= list[1] <= • • • <= list[n-1] for searchnum. Return its position if found. Otherwise return -1 */ int middle; if (left <= right) { middle = (left + right) / 2; switch(COMPARE(list[middle], searchnum)) { case -1: left = middle + 1; break; case 0: return middle; case 1: right = middle – 1; } } return -1; } 22/48

Binary search source #include <stdio. h> #define COMPARE(x, y) (((x) < (y))? -1 : ((x) == (y))? 0 : 1) #define NUM_EL 10 int binsearch(int list[], int searchnum, int left, int right); void main(void) { int nums[NUM_EL] = {5, 10, 22, 32, 45, 67, 73, 98, 99, 101}; int i, item, location; int left = 0; int right = NUM_EL – 1; for(i = 0; i < 10; ++i) printf(“%d”, nums[i]); printf(“n. Enter the item you are searching for: ”); scanf(“%d”, &item); location = binsearch(nums, item, left, right); if(location > -1) printf(“The item was found at index location %dthn”, location + 1); else printf(“The item was not found in the arrayn”); } 23/48

Binary search source (cont’d) int binsearch(int list[], int searchnum, int left, int right) { int middle; while(left <= right) { middle = (left + right) / 2; switch(COMPARE(list[middle], searchnum)) { case -1: left = middle + 1; break; case 0: return middle; case 1: right = middle - 1; } } return -1; } 24/48

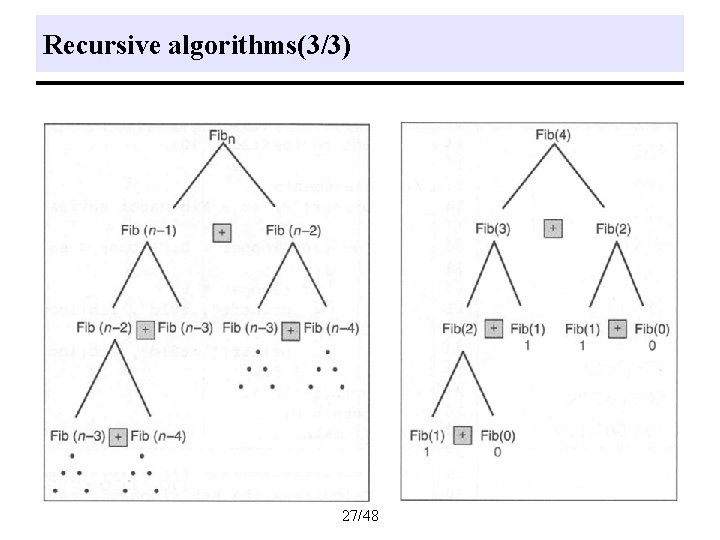
Recursive algorithms(1/3) q Recursion: Functions call themselves q Express a complex process in very clear terms – Any function can be written recursively – Good when the problem is defined recursively q (ex) Fibonacci numbers: each number is the sum of previous two numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … q Recursive design – Fibonacci(n) =0 if n = 0 =1 if n = 1 = Fibonacci(n-1) + Fibonacci(n-2) 25/48

Recursive algorithms(2/3) q Recursive algorithm long fib (long num) { // Base Case if (num == 0 || num == 1) return num; // General Case return (fib (num - 1) + fib (num - 2)); } // fib 26/48

Recursive algorithms(3/3) 27/48

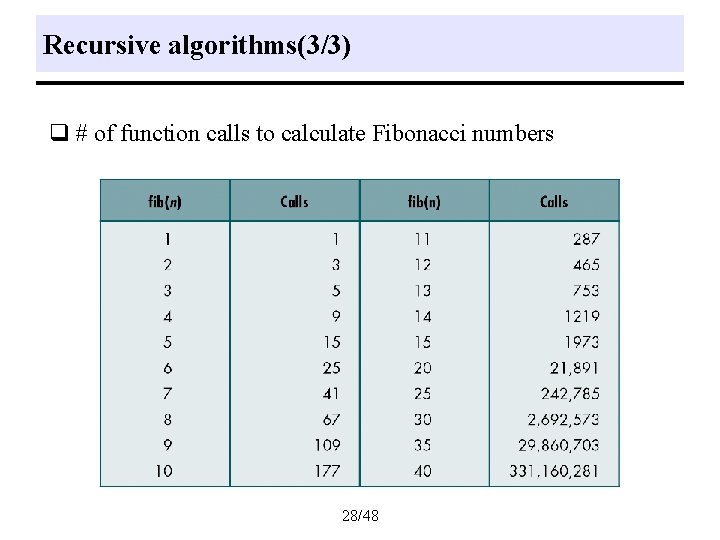
Recursive algorithms(3/3) q # of function calls to calculate Fibonacci numbers 28/48

(ex) Transformation of iterative program into recursive version q Establish boundary conditions that terminate the recursive calls q Implement the recursive calls so that each call brings us one step closer to a solution q (ex) Recursive implementation of binary search 29/48

(ex) Recursive implementation of binary search int binsearch(int list[], int searchnum, int left, int right) { /* search list[0] <= list[1] <= • • • <= list[n-1] for searchnum. Return its position if found. Otherwise return -1 */ int middle; if(left <= right) { middle = (left + right) / 2; switch(COMPARE(list[middle], searchnum)) { case -1: return binsearch(list, searchnum, middle + 1, right); case 0: return middle; case 1: return binsearch(list, searchnum, left, middle – 1); } } return -1; } 30/48

Recursion Properties q Recursion is effective for – Problems that are naturally recursive • Binary search – Algorithms that use a data structure naturally recursive • Tree q Problems of recursion – Function call overhead • Time • Stack memory – Stability 31/48

Data abstraction q The real world abstractions must be represented in terms of data types – Basic data types • integer, real, character, etc. – Array • collections of elements of the same basic data type • e. g. , int list[5] – Structure • collections of elements whose data types need not be the same • e. g. , struct student { char last_name; int student_id; char grade; } 32/48

Data abstraction (cont’d) q Data type – A collection of objects and a set of operations that act on those objects q Abstract data type : data type organized by – Specifications of objects • Requirements/properties of objects – Specifications of operations on the objects • Description of what the function does. • Names, arguments, result of each functions “What a data type can do. ” q Abstract data type does not include – Representation of objects – Implementation of operations “How it is done is hidden. ” q Data Structure is to implement an abstract data type in PL 33/48

Abstract data type Natural_Number q Objects – An ordered subrange of the integers (0. . . INT_MAX) q Functions – Nat_No – Boolean – Nat_No Zero() : : = return 0; Is_zero() : : = if (x) return FALSE; else return TRUE; Add(x, y) : : = if( (x+y) <= INT_MAX ) return x+y; else return INT_MAX Equal(x, y) : : = if( x=y ) return TRUE; else return FALSE; Successor(x) : : = if( (x+y) <= INT_MAX ) return x+1; Subtract(x, y) : : = if ( x<y ) return 0; else return x-y; 34/48

Performance Analysis q Criteria which we can judge a program – Does the program meet the original specifications of the task? – Does it work correctly? – Does the program contain documentation that shows how to use it and how it work? – Does the program effectively use functions to create logical units? – Is the program’s code readable? – Does the program efficiently use primary and secondary storage? – Is the program’s running time acceptable for the task? q Performance evaluation – Performance analysis: machine independent, complexity theory – Performance measurement: machine dependent running times 35/48

Space complexity q Space complexity – The amount of memory that it needs to run to completion q The space needed by a program is the sum of – Fixed space requirements – Variable space requirements • • S(P) = c + Sp(I) c: A constant representing the fixed space requirements I: An instance of the problem Sp(I): A function of the number, size, and values of the inputs and outputs associated with I 36/48

(ex) Space complexity q Simple arithmetic function float abc(float a, float b, float c) { return a + b * c + (a + b – c) / (a + b) + 4. 00; } q Iterative function for summing a list of numbers float sum(float list[], int n) { float tempsum = 0; int i; for(i = 0; i < n; i++) tempsum += list[i]; return tempsum; } q Recursive function for summing a list of numbers float rsum(float list[], int n) { if(n) return rsum(list, n - 1) + list[n-1]; return 0; } 37/48

Time complexity q Time complexity – The amount of computer time that it needs to run to completion q Program step – A syntactically meaningful program segment whose execution time is independent of the instance characteristics – e. g. , a = 2 * b + 3 * c / d – e + f / g / a / b / c 38/48

(ex) Iterative summing of a list of numbers float sum(float list[], int n) { float tempsum = 0; count++; int i; /* for assignment */ for(i = 0; i < n; i++) { count++; tempsum += list[i]; count++; } count++; return tempsum; /* for the for loop */ /* for assignment */ /* last execution of for */ /* for return */ } 39/48

(ex) Iterative summing of a list of numbers Statement s/e Frequency Total steps float sum(float list[], int n) { float tempsum = 0; int i; for(i = 0; i < n; i++) tempsum += list[i]; return tempsum; } Total 0 0 1 1 1 0 0 0 1 0 n+1 n 1 0 2 n+3 40/48

(ex) Matrix addition void add(int a[][MAX_SIZE], int b[][MAX_SIZE], int c[][MAX_SIZE], int rows, int cols) { int i, j; for(i = 0; i < rows; i++) { for(j = 0; j < cols; j++) count += 2; } count++; } 41/48

(ex) Matrix addition Statement s/e Frequency void add(int a[][MAX_SIZE]. . . ) { int i, j; for(i = 0; i < rows, i++) for(j = 0; j < cols; j++) c[i][j] = a[i][j] + b[i][j]; } 0 0 0 1 1 1 0 Total 0 0 0 rows+1 rows*(cols+1) rows*cols 0 Total steps 0 0 0 rows+1 rows*cols+rows*cols 0 2 rows*cols + 2 rows +1 42/48

Asymptotic notation (O, Ω, Θ) q Definition: a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity – Approximate notation : ex) 1000 n 2+4 n+2 – It is important that worst-case and best-case in algorithm performance q O : The worst-case of algorithm q Ω : The best-case of algorithm qΘ: O+Ω 43/48

Asymptotic notation (O, Ω, Θ) q Definition: [Big “oh”] – f(n) = O(g(n)) (read as “f of n is big oh of g of n”) iff (if and only if) there exist positive constants c and n 0 such that f(n)≤cg(n) for all n, n≥n 0 – e. g. , 3 n+2=O(n) as 3 n+2≤ 4 n for all n≥ 2 10 n 2+4 n+2=O(n 2) as 10 n 2+4 n+2≤ 11 n 2 for all n≥ 5 O(1), O(logn), O(nlogn), O(n 2), O(n 3), O(2 n), and O(n!) – g(n) is an upperbound on the value of f(n) for all n, n≥n 0 q Theorem 1. 2 – If f(n)=amnm+. . . + a 1 n+a 0, then f(n)=O(nm) 44/48

Asymptotic notation (O, Ω, Θ) q Definition: [Omega] – f(n) = Ω(g(n)) (read as “f of n is omega of g of n”) iff there exist positive constants c and n 0 such that f(n)≥cg(n) for all n, n≥n 0 – e. g. , 3 n+2=Ω(n) as 3 n+2≥ 3 n for all n≥ 1 10 n 2+4 n+2=Ω(n 2) as 10 n 2+4 n+2≥n 2 for all n≥ 1 – g(n) is only a lower bound on f(n) q Theorem 1. 3 – If f(n)=amnm+. . . + a 1 n+a 0, and am>0, then f(n)=Ω(nm) 45/48 n

Asymptotic notation (O, Ω, Θ) q Definition: [Theta] – f(n) = Θ(g(n)) (read as “f of n is theta of g of n”) iff there exist positive constants c 1, c 2, and n 0 such that c 1 g(n)≤f(n)≤c 2 g(n) for all n, n≥n 0 – e. g. , 3 n+2=Θ(n) as 3 n+2≥ 3 n for all n≥ 2 and 3 n+2≤ 4 n for all n≥ 2, so c 1=3, c 2=4, and n 0=2 10 n 2+4 n+2= Θ(n 2) – g(n) is both an upper and lower bound on f(n) q Theorem 1. 4 – If f(n)=amnm+. . . + a 1 n+a 0, and am>0, then f(n)= Θ(nm) 46/48 n

(ex) Complexity of matrix addition q Determine the asymptotic complexity of each statement q Take the maximum Statement Asymptotic complexity void add(int a[][MAX_SIZE]. . . ) { int i, j; for(i = 0; i < rows; i++) for(j = 0; j < cols; j++) c[i][j] = a[i][j] + b[i][j]; } 0 0 0 Θ(rows) Θ(rows*cols) 0 Total Θ(rows*cols) 47/48

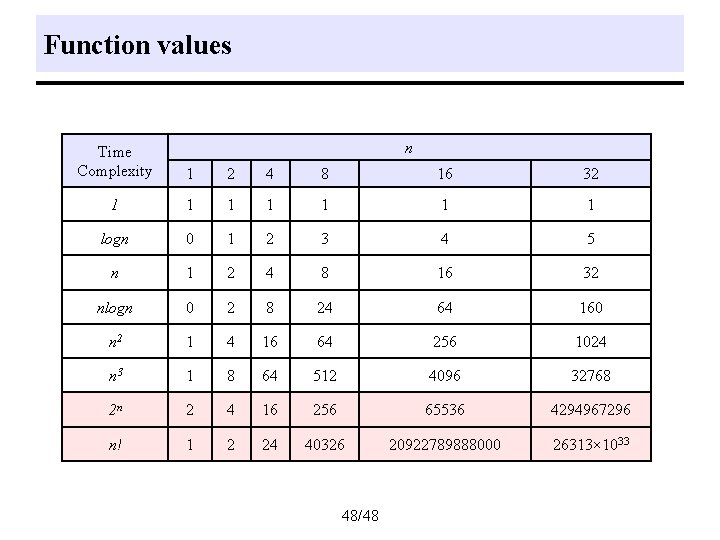
Function values n Time Complexity 1 2 4 8 16 32 1 1 1 1 logn 0 1 2 3 4 5 n 1 2 4 8 16 32 nlogn 0 2 8 24 64 160 n 2 1 4 16 64 256 1024 n 3 1 8 64 512 4096 32768 2 n 2 4 16 256 65536 4294967296 n! 1 2 24 40326 20922789888000 26313× 1033 48/48