Data Structures 4 th Week Chapter 2 Arrays

Data Structures 4 th Week Chapter 2 Arrays And Structures 2. 5 Representation Of Multidimensional Arrays 2. 6 The String Abstract Data Type Chapter 3 Stacks And Queues 3. 1 The Stack Abstract Data Type 3. 2 The Queue Abstract Data Type 3. 3 A Mazing Problem

Representation of multidimensional arrays q Two common ways to represent multidimensional arrays – Row major order – Column major order q Two-dimensional array A[upper 0][upper 1] – If α is the address of A[0][0] • The address of A[i][0] is α + i · upper 1 • The address of A[i][j] is α + i · upper 1 + j – If α is the address of A[0][0]. . . [0] • The address for A[i 0][i 1]. . . [in-1] is 2/

The String Abstract Data Type q String – Has the form S=s 0, . . . , sn-1, where si are characters taken form the character set of the programming language #define MAX_SIZE 100 /* maximum size of string */ char s[MAX_SIZE] = {“dog”}; char t[MAX_SIZE] = {“house”}; s[0] s[1] s[2] s[3] t[0] t[1] t[2] t[3] t[4] t[5] d o g n h o u s e n 3/

Abstract data type String q Object – A finite set of zero or more characters q Functions – – – String Null(m) Integer Compare(s, t) Boolean Is. Null(s) Integer Length(s) String Concat(s, t) String Substr(s, i, j) 4/

(ex) String insertion #include <string. h> #define MAX_SIZE 100 /* size of largest string */ char string 1[MAX_SIZE], *s = string 1; char string 2[MAX_SIZE], *t = string 2; s → a m o b t → u t o temp → i l e o b i initially temp → a (a) after strncpy(temp, s, i) temp → a u t o o m (a) after strcat(temp, t) temp → a u t (a) after strcat(temp, (s + i)) 5/ l e

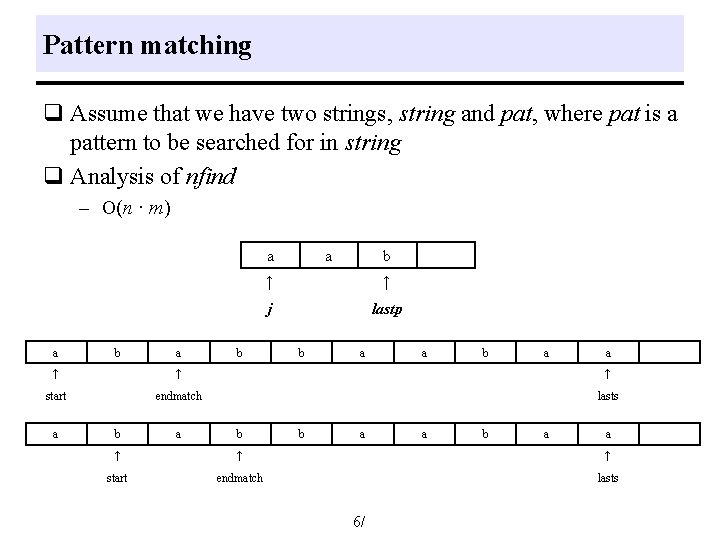
Pattern matching q Assume that we have two strings, string and pat, where pat is a pattern to be searched for in string q Analysis of nfind – O(n · m) a a b a b ↑ ↑ j lastp b a a ↑ ↑ ↑ start endmatch lasts a b b a a ↑ ↑ ↑ start endmatch lasts 6/

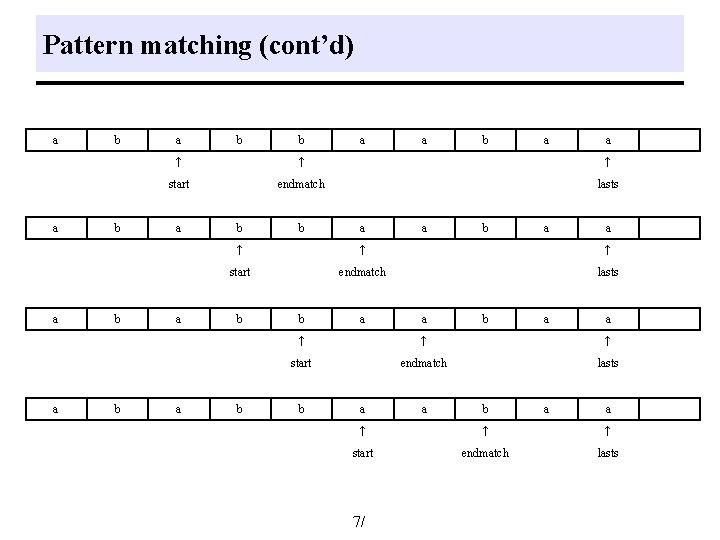
Pattern matching (cont’d) a a b b a a ↑ ↑ ↑ start endmatch lasts a a a b b a a b a a ↑ ↑ ↑ start endmatch lasts 7/

Chapter 3 Stacks And Queues

The stack abstract data type q Stack – An ordered list in which insertions and deletions are made at one end called the top – Given a stack S = (a 0, . . . , an-1), we say that a 0 is the bottom element, an-1 is the top element, and ai is on top of element ai-1, 0 < i < n q Last-In-First-Out (LIFO) list D C B A ← top C C B B B A A A 9/ top ← ← top

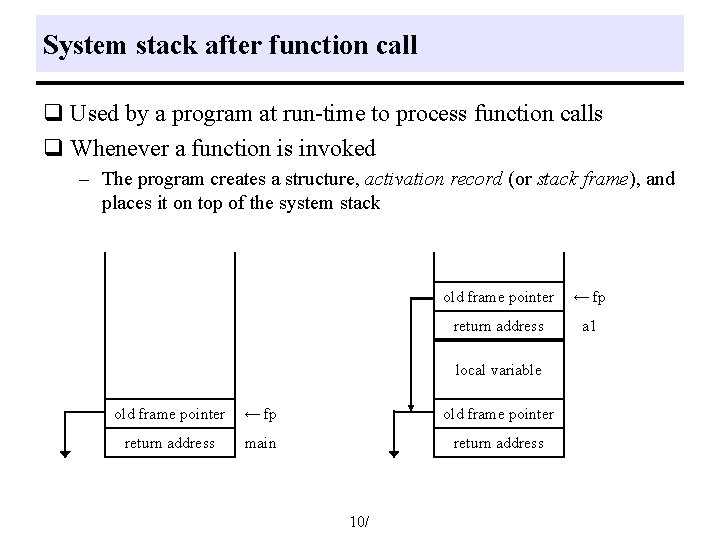
System stack after function call q Used by a program at run-time to process function calls q Whenever a function is invoked – The program creates a structure, activation record (or stack frame), and places it on top of the system stack old frame pointer ← fp return address a 1 local variable old frame pointer ← fp old frame pointer return address main return address 10/

Abstract data type Stack q Objects – A finite ordered list with zero or more elements q Functions – – – Stack Create. S(max_stack_size) Boolean Is. Full(stack, max_stack_size) Stack Add(stack, item) Boolean Is. Empty(stack) Element Delete(stack) 11/

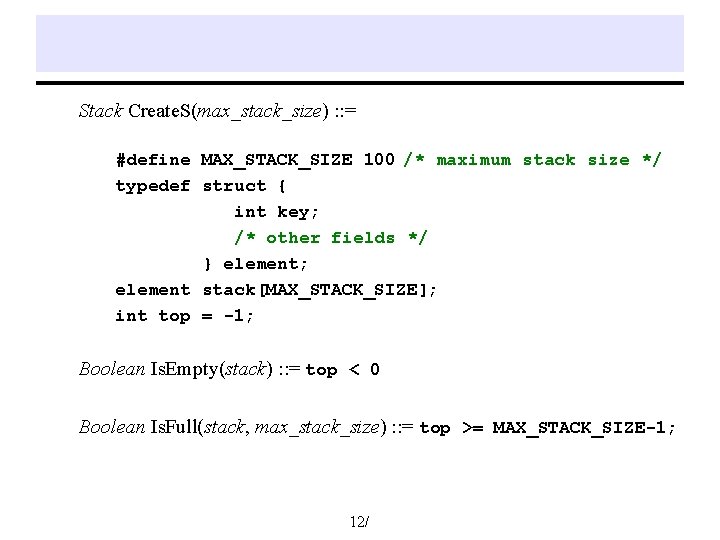
Stack Create. S(max_stack_size) : : = #define MAX_STACK_SIZE 100 /* maximum stack size */ typedef struct { int key; /* other fields */ } element; element stack[MAX_STACK_SIZE]; int top = -1; Boolean Is. Empty(stack) : : = top < 0 Boolean Is. Full(stack, max_stack_size) : : = top >= MAX_STACK_SIZE-1; 12/

(ex) Add to a stack & delete from a stack void add(int *top, element item) { /* add an item to the global stack */ if(*top >= MAX_STACK_SIZE-1) { stack_full(); return; } stack[++*top] = item; } element delete(int *top) { /* return the top element from the stack */ if(*top == -1) return stack_empty(); /* returns an error key */ return stack[(*top)--]; } 13/

The queue abstract data type q Queue – An ordered list in which all insertions take place at one end, called rear, and all deletions take place at the opposite end, called front – Given a queue Q = (a 0, a 1, . . . , an-1), a 0 is the front element, an-1 is the rear element, and ai+1 is behind ai, 0≤i≤n-1 q First-In-First-Out (FIFO) D C A ← rear ← front B ← rear B A ← front A ← ← 14/ rear front ← rear C D B C A ← front B ← rear ← front

(ex) Abstract data type Queue q Objects – A finite ordered list with zero or more elements q Functions – – – Queue Create. Q(max_queue_size) Boolean Is. Full. Q(queue, max_queue_size) Queue Add. Q(queue, item) Boolean Is. Empty. Q(queue) Element Delete. Q(queue) 15/

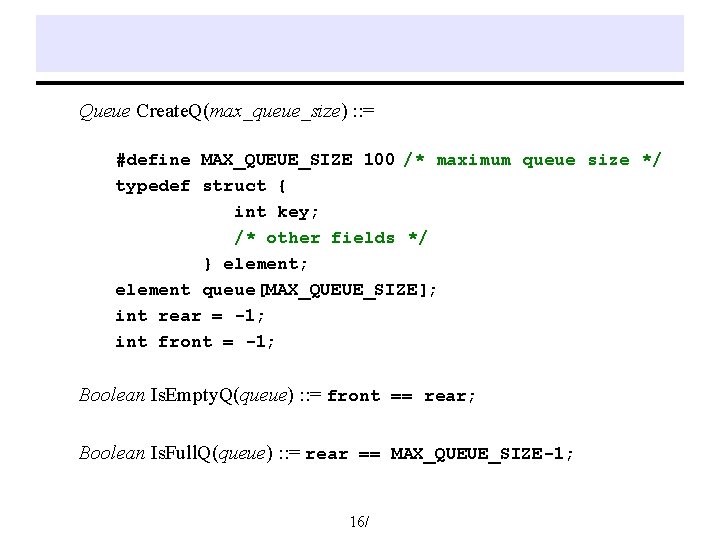
Queue Create. Q(max_queue_size) : : = #define MAX_QUEUE_SIZE 100 /* maximum queue size */ typedef struct { int key; /* other fields */ } element; element queue[MAX_QUEUE_SIZE]; int rear = -1; int front = -1; Boolean Is. Empty. Q(queue) : : = front == rear; Boolean Is. Full. Q(queue) : : = rear == MAX_QUEUE_SIZE-1; 16/

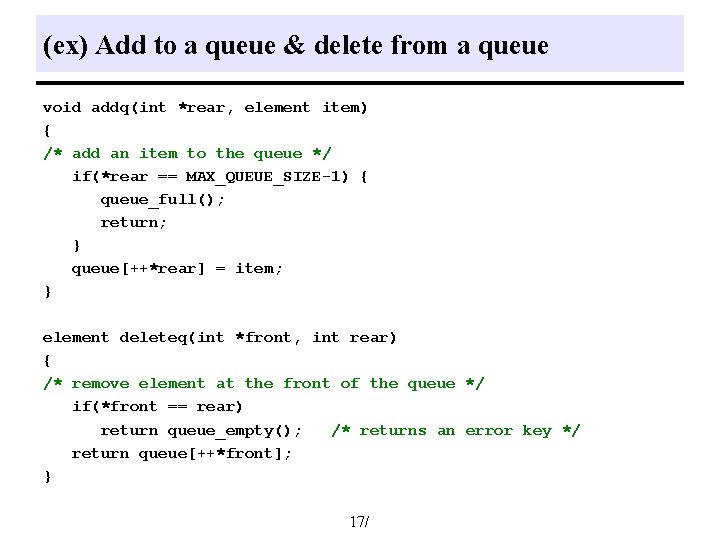
(ex) Add to a queue & delete from a queue void addq(int *rear, element item) { /* add an item to the queue */ if(*rear == MAX_QUEUE_SIZE-1) { queue_full(); return; } queue[++*rear] = item; } element deleteq(int *front, int rear) { /* remove element at the front of the queue */ if(*front == rear) return queue_empty(); /* returns an error key */ return queue[++*front]; } 17/

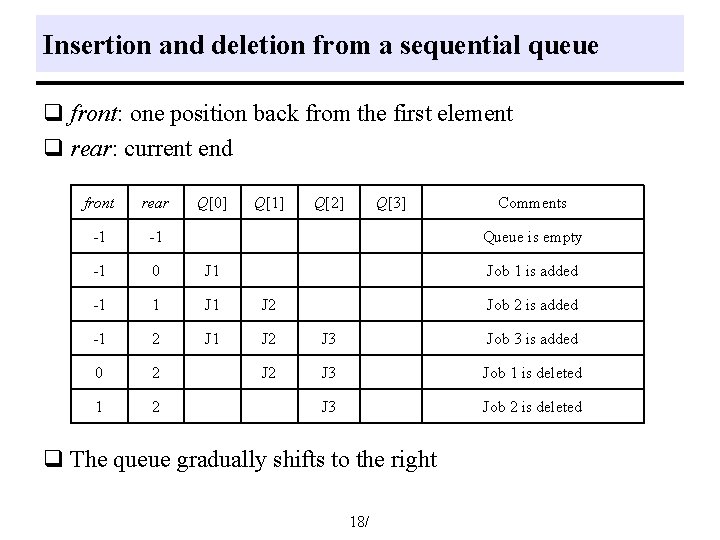
Insertion and deletion from a sequential queue q front: one position back from the first element q rear: current end front rear Q[0] Q[1] Q[2] Q[3] Comments -1 -1 -1 0 J 1 -1 1 J 2 -1 2 J 1 J 2 J 3 Job 3 is added 0 2 J 3 Job 1 is deleted 1 2 J 3 Job 2 is deleted Queue is empty Job 1 is added Job 2 is added q The queue gradually shifts to the right 18/

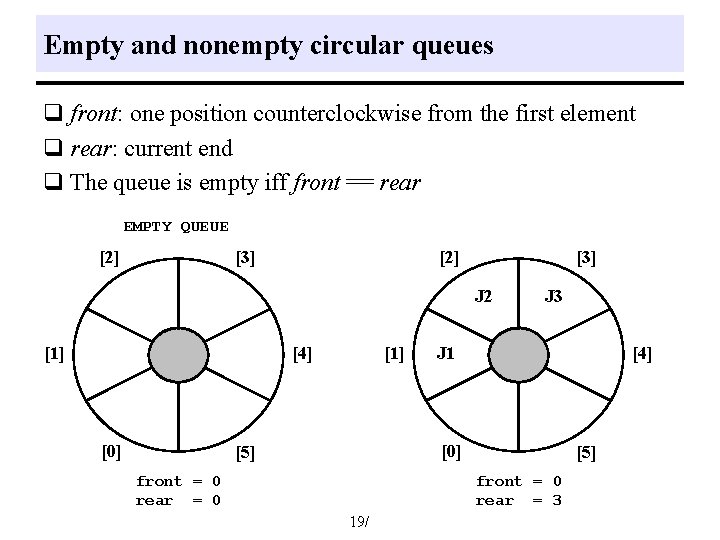
Empty and nonempty circular queues q front: one position counterclockwise from the first element q rear: current end q The queue is empty iff front == rear EMPTY QUEUE [2] [3] J 2 [1] [4] [0] [1] J 3 J 1 [4] [0] [5] front = 0 rear = 0 [5] front = 0 rear = 3 19/

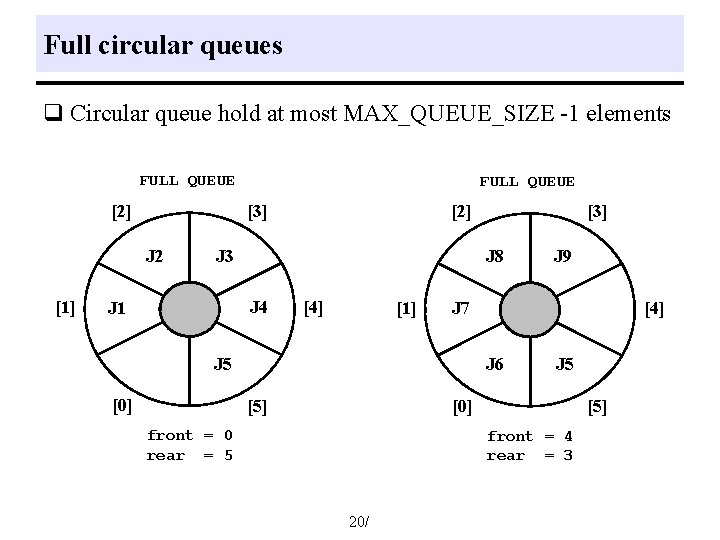
Full circular queues q Circular queue hold at most MAX_QUEUE_SIZE -1 elements FULL QUEUE [2] [3] J 2 [1] FULL QUEUE [2] J 3 J 8 J 4 J 1 [4] [1] [4] J 6 [5] J 9 J 7 J 5 [0] [3] J 5 [0] front = 0 rear = 5 [5] front = 4 rear = 3 20/

(ex) Add to a circular queue & delete from a circular queue void addq(int front, int *rear, element item) { /* add an item to the queue */ *rear = (*rear + 1) / MAX_QUEUE_SIZE; if(front == *rear) { queue_full(rear); /* reset rear and print error */ return; } queue[*rear] = item; } element deleteq(int *front, int rear) { element item; /* remove front element from the queue and put it in item */ if(*front == rear) return queue_empty(); /* queue_empty returns an error key */ *front = (*front + 1) % MAX_QUEUE_SIZE; return queue[*front]; } 21/

A mazing problem q An example maze entrance → 0 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 0 → 22/ exit

typedef struct { short int vert; short int horiz; } offsets; offsets move[8]; /* array of moves for each direction */ next_row = row + move[dir]. vert; next_col = col + move[dir]. horiz; #define MAX_STACK_SIZE 100 /* maximum stack size */ typedef struct { short int row; short int col; short int dir; } element; element stack[MAX_STACK_SIZE]; 23/

Table of moves Name Dir move[dir]. vert move[dir]. horiz N 0 -1 0 NE 1 -1 1 E 2 0 1 SE 3 1 1 S 4 1 0 SW 5 1 -1 W 6 0 -1 NW 7 -1 -1 24/

q Analysis of path – Stack size • Since each position is visited no more than once, the stack needs to have only as many positions as there are zeros – The worst case complexity of the algorithm is O(mp), where m and p are the number of rows and columns of the maze 25/