Data Structures 2 nd Week Chapter 1 Basic

Data Structures 2 nd Week Chapter 1 Basic Concepts 1. 3 abstract data type 1. 4 Performance Analysis – space and time complexity

Chapter 1 Basic Concepts

Data abstraction q The real world abstractions must be represented in terms of data types – Basic data types • integer, real, character, etc. – Array • collections of elements of the same basic data type • e. g. , int list[5] – Structure • collections of elements whose data types need not be the same • e. g. , struct student { char last_name; int student_id; char grade; } 3/23

Data abstraction (cont’d) q Data type – A collection of objects and a set of operations that act on those objects q Abstract data type: data type organized by – Specifications of objects • Requirements/properties of objects – Specifications of operations on the objects • Description of what the function does. • Names, arguments, result of each functions “What a data type can do. ” q Abstract data type does not include – Representation of objects – Implementation of operations “How it is done is hidden. ” q Data Structure is to implement an abstract data type in PL 4/23

Abstract data type Natural_Number q Objects – An ordered subrange of the integers (0. . . INT_MAX) q Functions – – – Nat_No Boolean Nat_No Zero( ) Is_Zero(x) Add(x, y) Equal(x, y) Successor(x) Subtract(x, y) 5/23

Performance Analysis q Criteria which we can judge a program – Does the program meet the original specifications of the task? – Does it work correctly? – Does the program contain documentation that shows how to use it and how it work? – Does the program effectively use functions to create logical units? – Is the program’s code readable? – Does the program efficiently use primary and secondary storage? – Is the program’s running time acceptable for the task? q Performance evaluation – Performance analysis: machine independent, complexity theory – Performance measurement: machine dependant running times 6/25

Space complexity q Space complexity – The amount of memory that it needs to run to completion q The space needed by a program is the sum of – Fixed space requirements – Variable space requirements • • S(P) = c + Sp(I) c: A constant representing the fixed space requirements I: An instance of the problem Sp(I): A function of the number, size, and values of the inputs and outputs associated with I 7/25

(ex) Space complexity q Simple arithmetic function float abc(float a, float b, float c) { return a + b * c + (a + b – c) / (a + b) + 4. 00; } q Iterative function for summing a list of numbers float sum(float list[], int n) { float tempsum = 0; int i; for(i = 0; i < n; i++) tempsum += list[i]; return tempsum; } q Recursive function for summing a list of numbers float rsum(float list[], int n) { if(n) return rsum(list, n - 1) + list[n-1]; return 0; } 8/25

Time complexity q Time complexity – The amount of computer time that it needs to run to completion q Program step – A syntactically meaningful program segment whose execution time is independent of the instance characteristics – e. g. , a = 2 * b + 3 * c / d – e + f / g / a / b / c 9/25

(ex) Iterative summing of a list of numbers float sum(float list[], int n) { float tempsum = 0; count++; int i; /* for assignment */ for(i = 0; i < n; i++) { count++; tempsum += list[i]; count++; } count++; return tempsum; /* for the for loop */ /* for assignment */ /* last execution of for */ /* for return */ } 10/25

Statement s/e Frequency Total steps float sum(float list[], int n) { float tempsum = 0; int i; for(i = 0; i < n; i++) tempsum += list[i]; return tempsum; } Total 0 0 1 1 1 0 0 0 1 0 n+1 n 1 0 2 n+3 11/25

(ex) Matrix addition void add(int a[][MAX_SIZE], int b[][MAX_SIZE], int c[][MAX_SIZE], int rows, int cols) { int i, j; for(i = 0; i < rows; i++) { for(j = 0; j < cols; j++) count += 2; } count++; } 12/25

Statement s/e Frequency void add(int a[][MAX_SIZE]. . . ) { int i, j; for(i = 0; i < rows, i++) for(j = 0; j < cols; j++) c[i][j] = a[i][j] + b[i][j]; } 0 0 0 1 1 1 0 Total 0 0 0 rows+1 rows*(cols+1) rows*cols 0 Total steps 0 0 0 rows+1 rows*cols+rows*cols 0 2 rows*cols + 2 rows +1 13/25

Asymptotic notation (O, Ω, Θ) q Definition: [Big “oh”] – f(n) = O(g(n)) (read as “f of n is big oh of g of n”) iff (if and only if) there exist positive constants c and n 0 such that f(n)≤cg(n) for all n, n≥n 0 – e. g. , 3 n+2=O(n) as 3 n+2≤ 4 n for all n≥ 2 10 n 2+4 n+2=O(n 2) as 10 n 2+4 n+2≤ 11 n 2 for all n≥ 5 O(1), O(logn), O(nlogn), O(n 2), O(n 3), O(2 n), and O(n!) – g(n) is an upperbound on the value of f(n) for all n, n≥n 0 q Theorem 1. 2 – If f(n)=amnm+. . . + a 1 n+a 0, then f(n)=O(nm) 14/25

Asymptotic notation (O, Ω, Θ) q Definition: [Omega] – f(n) = Ω(g(n)) (read as “f of n is omega of g of n”) iff there exist positive constants c and n 0 such that f(n)≥cg(n) for all n, n≥n 0 – e. g. , 3 n+2=Ω(n) as 3 n+2≥ 3 n for all n≥ 1 10 n 2+4 n+2=Ω(n 2) as 10 n 2+4 n+2≥n 2 for all n≥ 1 – g(n) is only a lower bound on f(n) q Theorem 1. 3 – If f(n)=amnm+. . . + a 1 n+a 0, and am>0, then f(n)=Ω(nm) 15/25

Asymptotic notation (O, Ω, Θ) q Definition: [Theta] – f(n) = Θ(g(n)) (read as “f of n is theta of g of n”) iff there exist positive constants c 1, c 2, and n 0 such that c 1 g(n)≤f(n)≤c 2 g(n) for all n, n≥n 0 – e. g. , 3 n+2=Θ(n) as 3 n+2≥ 3 n for all n≥ 2 and 3 n+2≤ 4 n for all n≥ 2, so c 1=3, c 2=4, and n 0=2 10 n 2+4 n+2= Θ(n 2) – g(n) is both an upper and lower bound on f(n) q Theorem 1. 4 – If f(n)=amnm+. . . + a 1 n+a 0, and am>0, then f(n)= Θ(nm) 16/25

(ex) Complexity of matrix addition q Determine the asymptotic complexity of each statement q Take the maximum Statement Asymptotic complexity void add(int a[][MAX_SIZE]. . . ) { int i, j; for(i = 0; i < rows; i++) for(j = 0; j < cols; j++) c[i][j] = a[i][j] + b[i][j]; } 0 0 0 Θ(rows) Θ(rows*cols) 0 Total Θ(rows*cols) 17/25

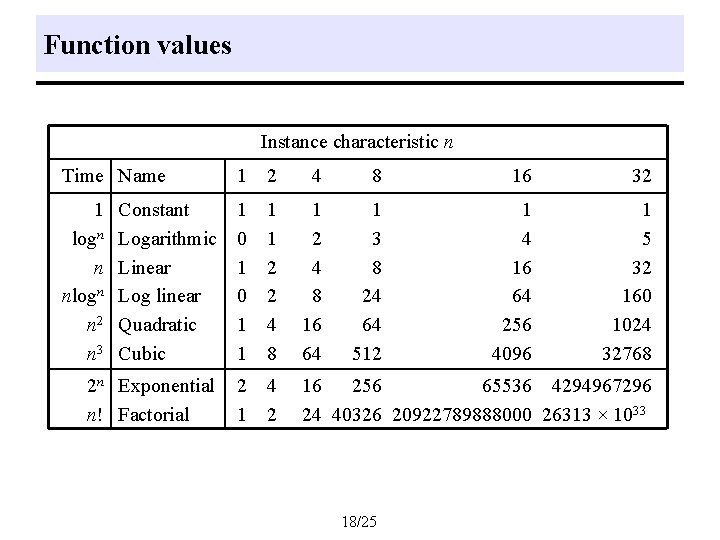
Function values Instance characteristic n Time Name 1 2 4 8 16 32 1 logn n nlogn n 2 n 3 Constant Logarithmic Linear Log linear Quadratic Cubic 1 0 1 1 2 2 4 8 16 64 1 3 8 24 64 512 1 4 16 64 256 4096 1 5 32 160 1024 32768 2 n Exponential n! Factorial 2 1 4 2 16 256 65536 4294967296 24 40326 20922789888000 26313 × 1033 18/25