Data Structure Data and data type Abstract data

Data Structure § § § Data and data type Abstract data type Lists List ADT Stack ADT Queue ADT 1

Data and Data Type q A type is a collection of values. For example, the Boolean type consists of the values true and false. q. A data type is a type together with a collection of operations to manipulate the type. For example, an integer variable is a member of the integer data type. Addition is an example of an operation on the integer data type. 2

Abstract Data Types (ADT) q. Language independent ØAbstract Data Type ØAn ADT is the specification of a data type within some language, independent of an implementation. ØThe interface for the ADT is defined in terms of a type and a set of operations on that type. 3

ADT q A data structure is the implementation for an ADT. In an object-oriented language, an ADT and its implementation together make up a class. Each operation associated with the ADT is implemented by a member function or method. q ADT is a type (or class) for objects whose behaviour is defined by a set of value and a set of operations. 4
ADT 5

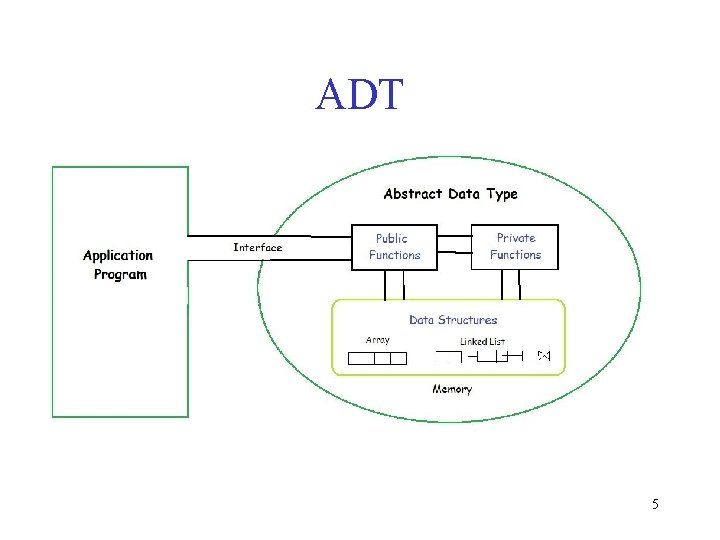
ADT q The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented. q It does not specify how data will be organized in memory and what algorithms will be used for implementing the operations. q It is called “abstract” because it gives an implementation-independent view. The process of providing only the essentials and hiding the details is known as abstraction. 6

ADT q. The user of data type does not need to know how that data type is implemented. q For example, we have been using Primitive values like int, float, char data types only with the knowledge that these data type can operate and be performed on without any idea of how they are implemented. 7

ADT q. So a user only needs to know what a data type can do, but not how it will be implemented. Think of ADT as a black box which hides the inner structure and design of the data type. 8

ADT q. So a user only needs to know what a data type can do, but not how it will be implemented. Think of ADT as a black box which hides the inner structure and design of the data type. 9

Relationship between logical and physical forms for data types q Data types have both a logical form and a physical form. The definition of the data type in terms of an ADT is its logical form. The implementation of the data type as a data structure is its physical form. q When you implement an ADT, you are dealing with the physical form of the associated data type. When you use an ADT elsewhere in your program, you are concerned with the associated data type's logical form. 10

Relationship between logical and physical forms for data types q The ADT defines the logical form of the data type. The data structure implements the physical form of the data type. Users of an ADT are typically programmers working in the same language as the implementer of the ADT. q Typically, these programmers want to use the ADT as a component in another application. The interface to an ADT is also commonly referred to as the Application Programmer Interface, or API, for the ADT. The interface becomes a form of communication between the two programmers. 11

Abstract Data Types Data object Set or collection of instances integer = {0, +1, -1, +2, -2, +3, -3, …} days. Of. Week = {S, M, T, W, Th, F, Sa} 12

Data Object instances may or may not be related my. Data. Object = {apple, chair, 2, 5. 2, red, green, Jack} 13

Data Structure Data object + relationships that exist among instances and elements that comprise an instance Among instances of integer 369 < 370 280 + 4 = 284 14

Data Structure Among elements that comprise an instance 369 3 is more significant than 6 3 is immediately to the left of 6 9 is immediately to the right of 6 15

Data Structure The relationships are usually specified by specifying operations on one or more instances. add, subtract, predecessor, multiply 16

Linear (or Ordered) Lists instances are of the form (e 0, e 1, e 2, …, en-1) where ei denotes a list element n >= 0 is finite list size is n 17

Linear Lists L = (e 0, e 1, e 2, e 3, …, en-1) relationships e 0 is the zero’th (or front) element en-1 is the last element ei immediately precedes ei+1 18

Linear List Examples/Instances Students in My. Class = (Jack, Jill, Abe, Henry, Mary, …, Judy) Exams in My. Class = (exam 1, exam 2, exam 3) Days of Week = (S, M, T, W, Th, F, Sa) Months = (Jan, Feb, Mar, Apr, …, Nov, Dec) 19

Linear List Operations—Length() determine number of elements in list L = (a, b, c, d, e) length = 5 20

Linear List Operations— Retrieve(the. Index) retrieve element with given index L = (a, b, c, d, e) Retrieve(0) = a Retrieve(2) = c Retrieve(4) = e Retrieve(-1) = error Retrieve(9) = error 21

Linear List Operations— Index. Of(the. Element) determine the index of an element L = (a, b, d, b, a) Index. Of(d) = 2 Index. Of(a) = 0 Index. Of(z) = -1 22

Linear List Operations— Delete(the. Index) delete and return element with given index L = (a, b, c, d, e, f, g) Delete(2) returns c and L becomes (a, b, d, e, f, g) index of d, e, f, and g decrease by 1 23

Linear List Operations— Delete(the. Index) delete and return element with given index L = (a, b, c, d, e, f, g) Delete(-1) => error Delete(20) => error 24

Linear List Operations— Insert(the. Index, the. Element) insert an element so that the new element has a specified index L = (a, b, c, d, e, f, g) Insert(0, h) => L = (h, a, b, c, d, e, f, g) index of a, b, c, d, e, f, and g increase by 1 25

Linear List Operations— Insert(the. Index, the. Element) L = (a, b, c, d, e, f, g) Insert(2, h) => L = (a, b, h, c, d, e, f, g) index of c, d, e, f, and g increase by 1 Insert(10, h) => error Insert(-6, h) => error 26

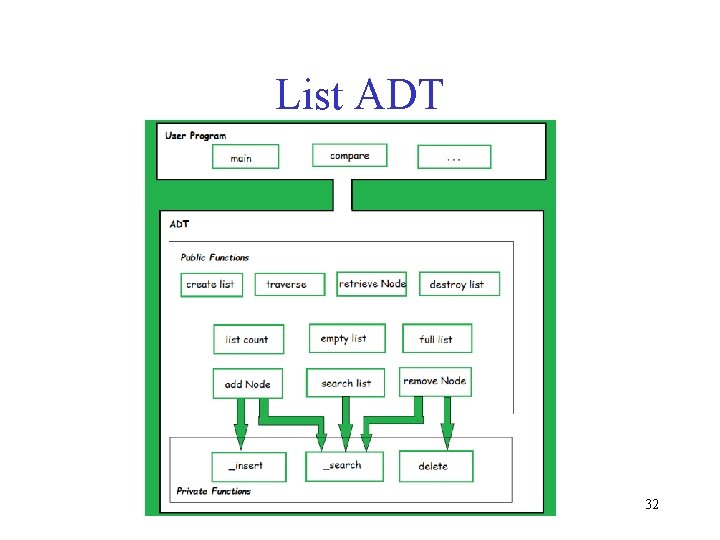
Linear List Abstract Data Type Abstract. Data. Type Linear. List { instances ordered finite collections of zero or more elements operations Is. Empty(): return true iff the list is empty, false otherwise Length(): return the list size (i. e. , number of elements in the list) Retrieve(index): return the indexth element of the list Index. O f(x): return the index of the first occurrence of x in the list, return -1 if x is not in the list Delete(index): remove and return the indexth element, elements with higher index have their index reduced by 1 Insert(the. Index, x): insert x as the indexth element, elements with the. Index >= index have their index increased by 1 } 27

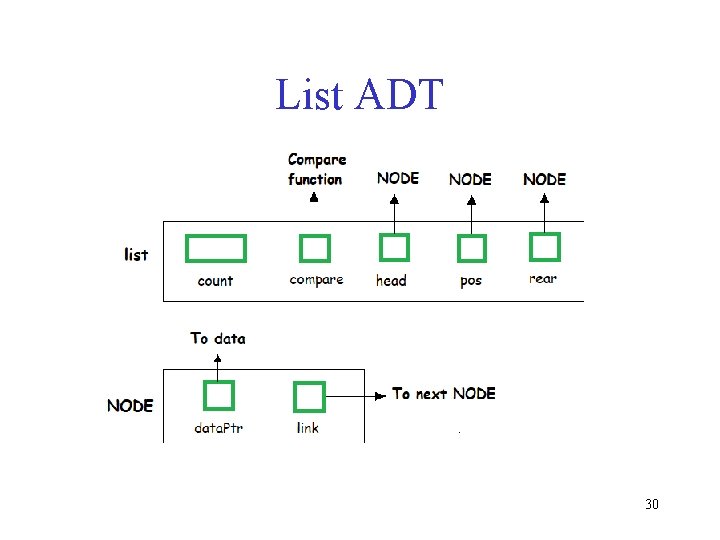
List ADT q. The data is generally stored in key sequence in a list which has a head structure consisting of count, pointers and address of compare function needed to compare the data in the list. § The data node contains the pointer to a data structure and a self-referential pointer which points to the next node in the list. 28 §

List ADT q. The data is generally stored in key sequence in a list which has a head structure consisting of count, pointers and address of compare function needed to compare the data in the list. § The data node contains the pointer to a data structure and a self-referential pointer which points to the next node in the list. 29
List ADT 30

List ADT The data node contains the pointer to a data structure and a self-referential pointer which points to the next node in the list. //List ADT Type Definitions typedef struct node { void *Data. Ptr; struct node *link; } Node; typedef struct { int count; Node *pos; Node *head; Node *rear; int (*compare) (void *argument 1, void *argument 2) } LIST; 31
List ADT 32

List ADT Functions • get() – Return an element from the list at any given position. • insert() – Insert an element at any position of the list. • remove() – Remove the first occurrence of any element from a non-empty list. • remove. At() – Remove the element at a specified location from a non-empty list. • replace() – Replace an element at any position by another element. • size() – Return the number of elements in the list. • is. Empty() – Return true if the list is empty, otherwise return false. • is. Full() – Return true if the list is full, otherwise return false. 33

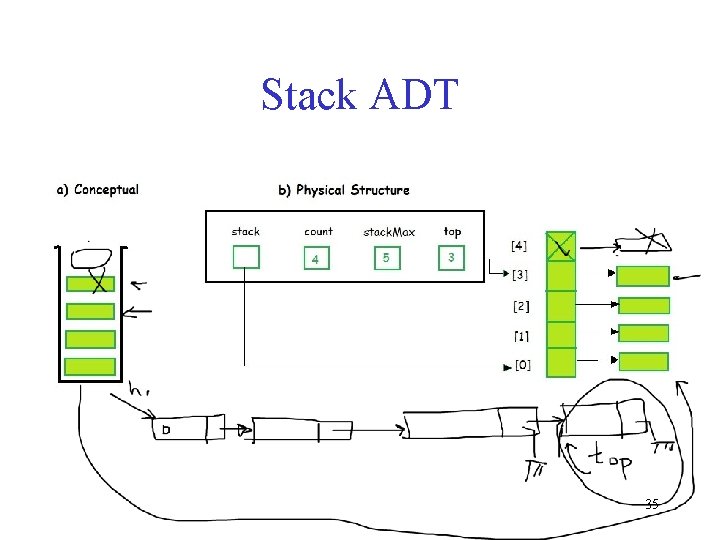
Stack ADT § In Stack ADT Implementation instead of data being stored in each node, the pointer to data is stored. § The program allocates memory for the data and address is passed to the stack ADT. § The head node and the data nodes are encapsulated in the ADT. The calling function can only see the pointer to the stack. § The stack head structure also contains a pointer to top and count of number of entries currently in stack. 34
Stack ADT 35

Stack ADT //Stack ADT Type Definitions typedef struct node { void *Data. Ptr; struct node *link; } Stack. Node; typedef struct { int count; Stack. Node *top; } STACK; 36

Stack ADT Functions • push() – Insert an element at one end of the stack called top. • pop() – Remove and return the element at the top of the stack, if it is not empty. • peek() – Return the element at the top of the stack without removing it, if the stack is not empty. • size() – Return the number of elements in the stack. • is. Empty() – Return true if the stack is empty, otherwise return false. • is. Full() – Return true if the stack is full, otherwise return false. 37

Stack ADT § In Stack ADT Implementation instead of data being stored in each node, the pointer to data is stored. § The program allocates memory for the data and address is passed to the stack ADT. § The head node and the data nodes are encapsulated in the ADT. The calling function can only see the pointer to the stack. § The stack head structure also contains a pointer to top and count of number of entries currently in stack. 38

Queue ADT § The queue abstract data type (ADT) follows the basic design of the stack abstract data type. § Each node contains a void pointer to the data and the link pointer to the next element in the queue. The program’s responsibility is to allocate memory for storing the data. 39
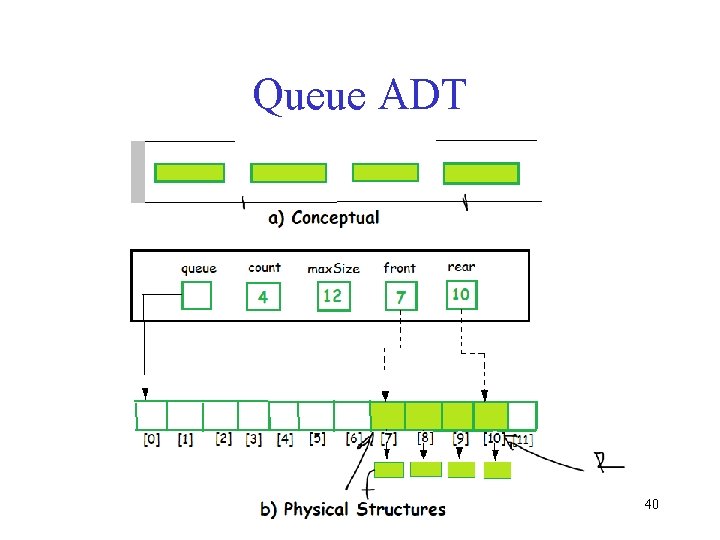
Queue ADT 40
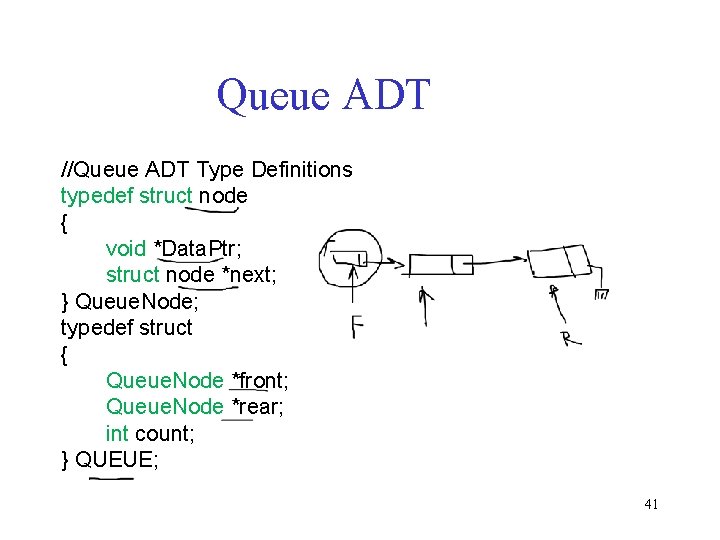
Queue ADT //Queue ADT Type Definitions typedef struct node { void *Data. Ptr; struct node *next; } Queue. Node; typedef struct { Queue. Node *front; Queue. Node *rear; int count; } QUEUE; 41

Queue ADT Functions • push() – Insert an element at one end of the stack called top. • pop() – Remove and return the element at the top of the stack, if it is not empty. • peek() – Return the element at the top of the stack without removing it, if the stack is not empty. • size() – Return the number of elements in the stack. • is. Empty() – Return true if the stack is empty, otherwise return false. • is. Full() – Return true if the stack is full, otherwise return false. 42

Stack ADT Functions • enqueue() – Insert an element at the end of the queue. • dequeue() – Remove and return the first element of the queue, if the queue is not empty. • peek() – Return the element of the queue without removing it, if the queue is not empty. • size() – Return the number of elements in the queue. • is. Empty() – Return true if the queue is empty, otherwise return false. • is. Full() – Return true if the queue is full, otherwise return false. 43

ADT § There can be different ways to implement an ADT. § For example, the List ADT can be implemented using arrays, or singly linked list or doubly linked list. Similarly, stack ADT and Queue ADT can be implemented using arrays or linked lists. 44
- Slides: 44