Data Structure Algorithm 10 Graph BFS DFS JJCAO

Data Structure & Algorithm 10 – Graph & BFS & DFS JJCAO

Graph Are Not 2

Can be very complex. Excellent Tool! 4

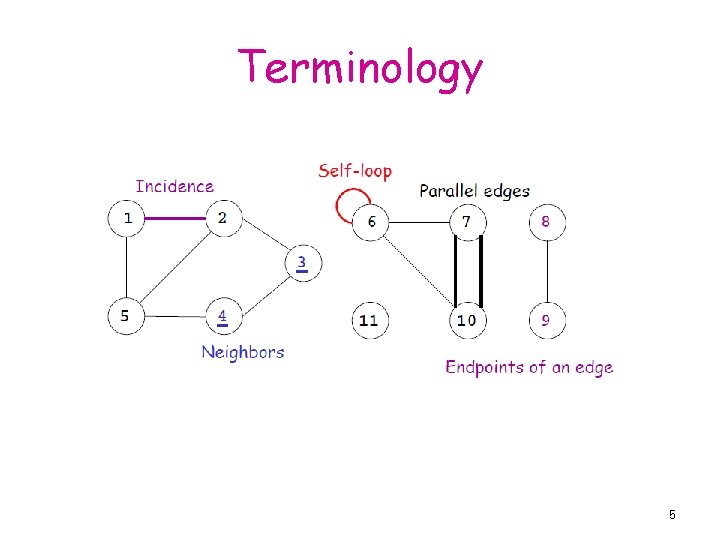
Terminology 5

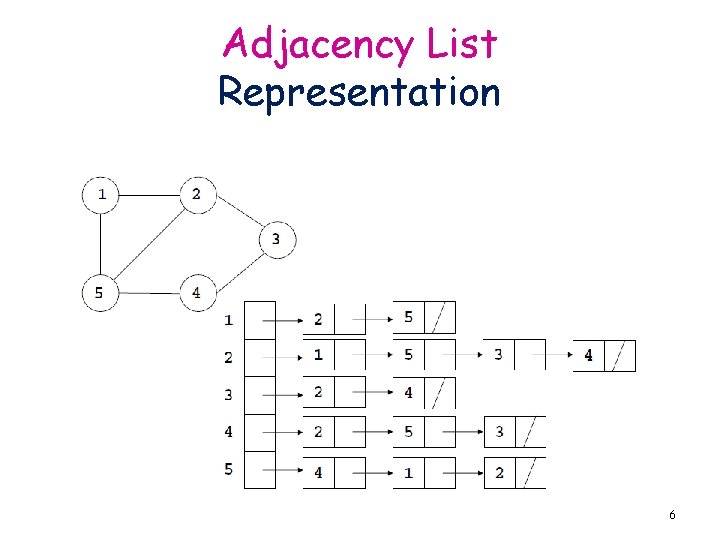
Adjacency List Representation 6

Adjacency Matrix Representation 7

Object-Oriented Representation • Node: some structure, with all relevant information • Edge: name & pointers to two endpoints 8

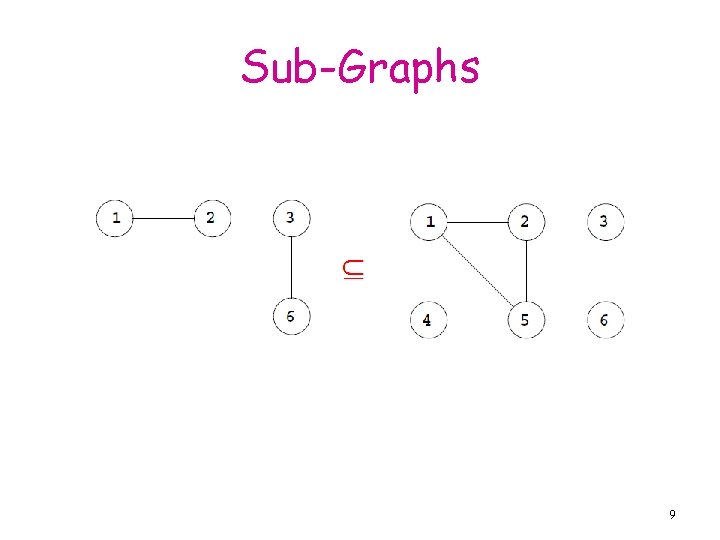
Sub-Graphs 9

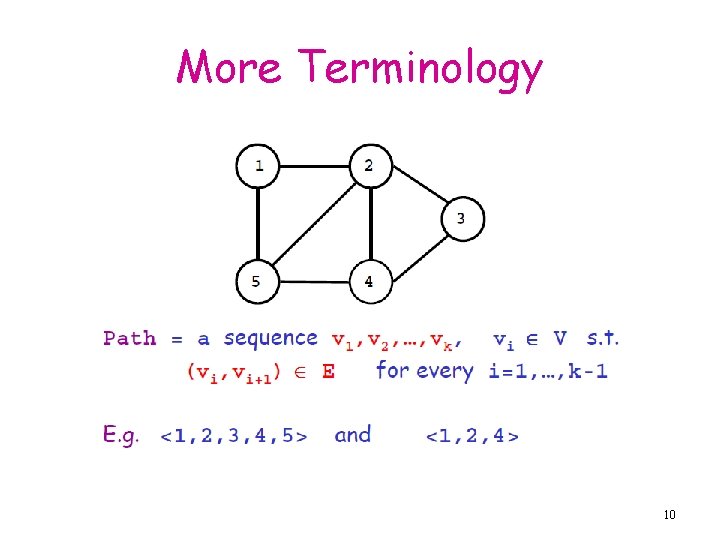
More Terminology 10

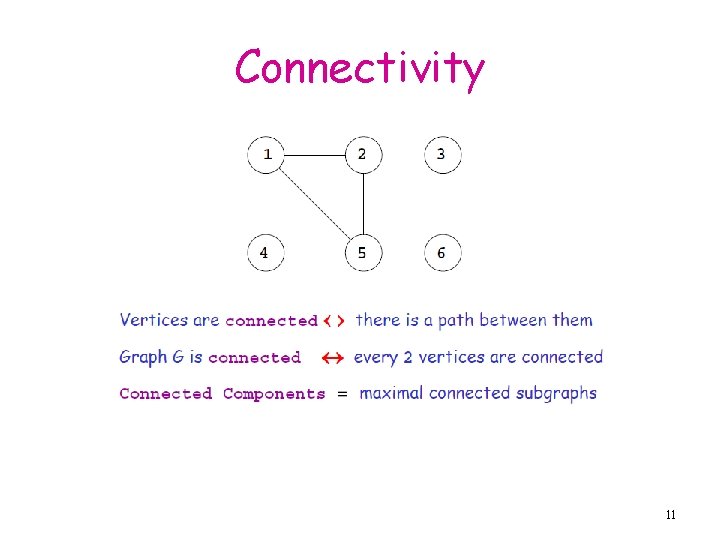
Connectivity 11

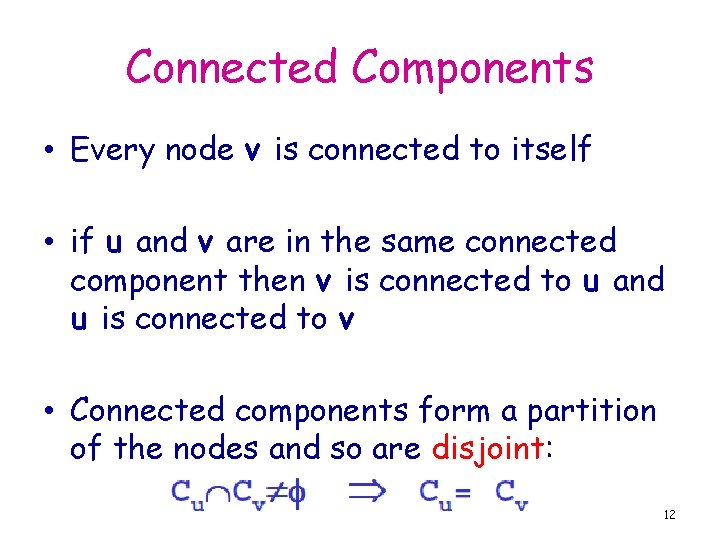
Connected Components • Every node v is connected to itself • if u and v are in the same connected component then v is connected to u and u is connected to v • Connected components form a partition of the nodes and so are disjoint: 12

Forests & Trees 13

Properties 14

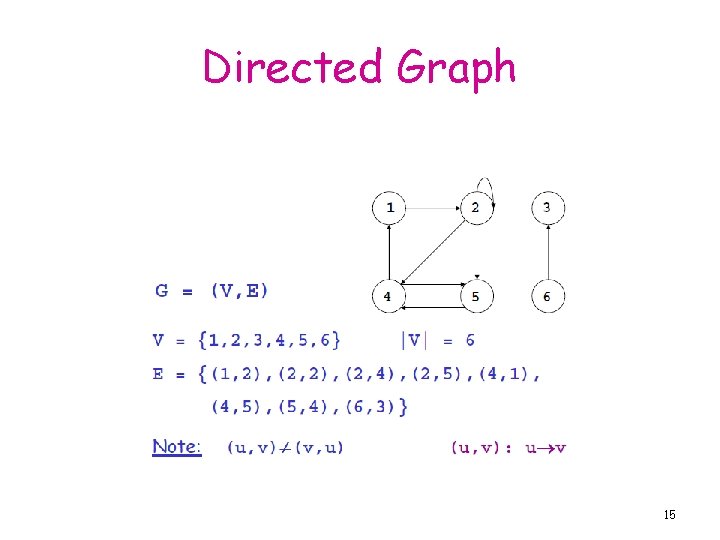
Directed Graph 15

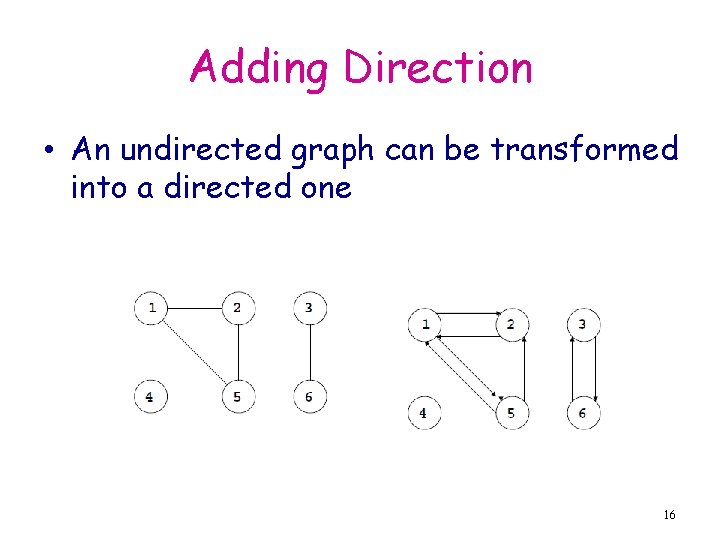
Adding Direction • An undirected graph can be transformed into a directed one 16

Terminology • endpoints of an edge = the vertices it connects • e = (u, v) is incident from u = leaves u incident to v = enters v – u is the tail – v is the head • degree of v = indegree + outdegree – indegree = # incoming edges – outdegree = # outgoing edges • Paths and cycles are now directed 17

Simple Graphs Are graphs with no parallel edges, no self loops Properties: 18

More Properties 19

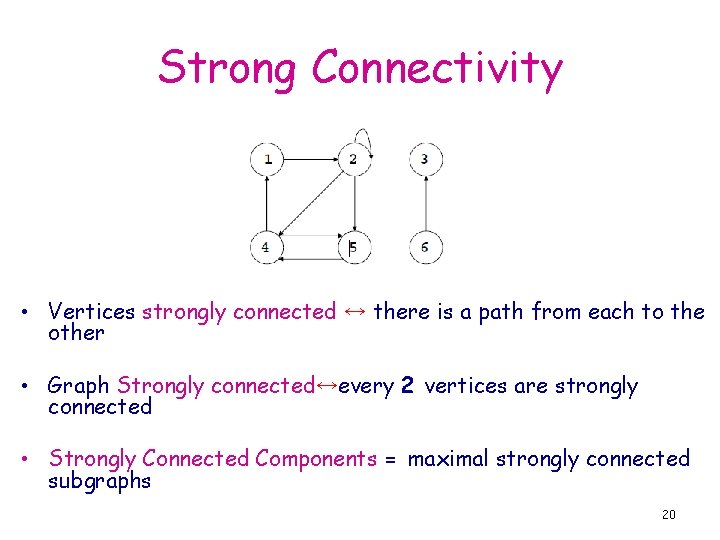
Strong Connectivity • Vertices strongly connected ↔ there is a path from each to the other • Graph Strongly connected↔every 2 vertices are strongly connected • Strongly Connected Components = maximal strongly connected subgraphs 20

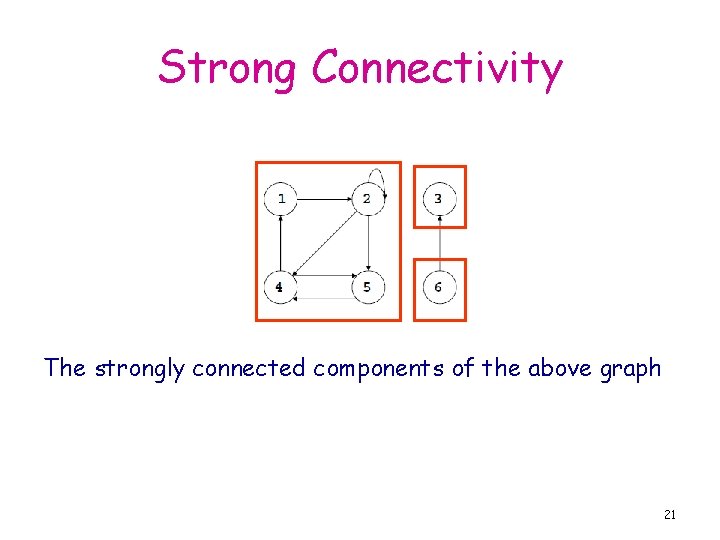
Strong Connectivity The strongly connected components of the above graph 21

Graph Traversals Given: a graph G a source vertex s in V[G] Goal: “visit” all the vertices of G to determine some property: – Is G connected? – Does G contain a cycle? – is there a v u path in G? – What is the shortest path connecting v and u? – Will G disconnect if we remove a single edge? A vertex? – G is the WWW - follow links to retrieve information…. 22

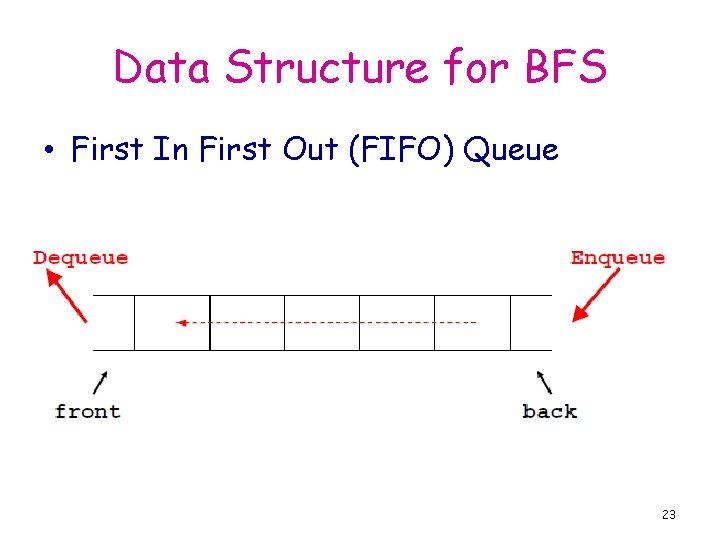
Data Structure for BFS • First In First Out (FIFO) Queue 23

Breadth First Search 24

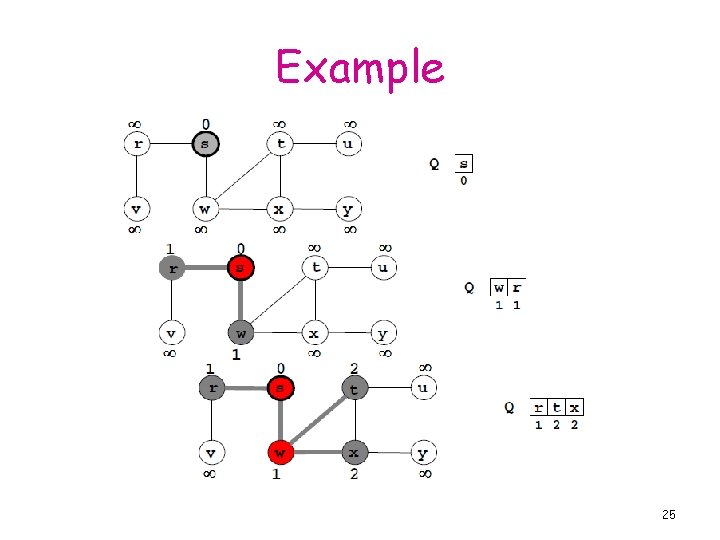
Example 25

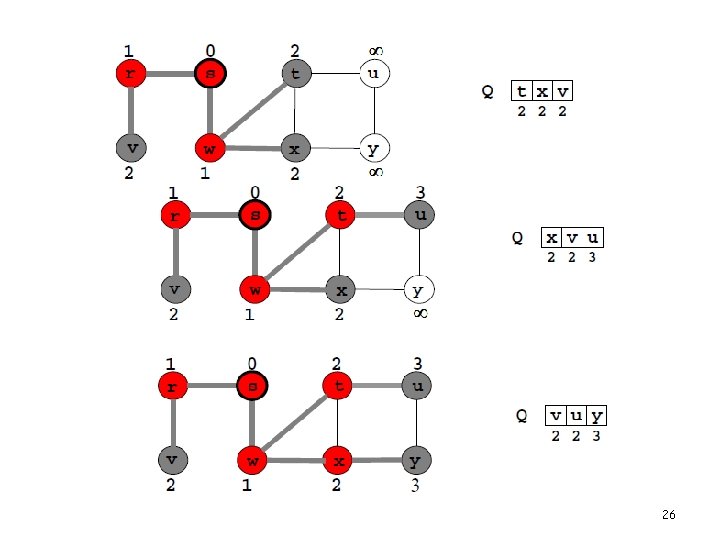
26

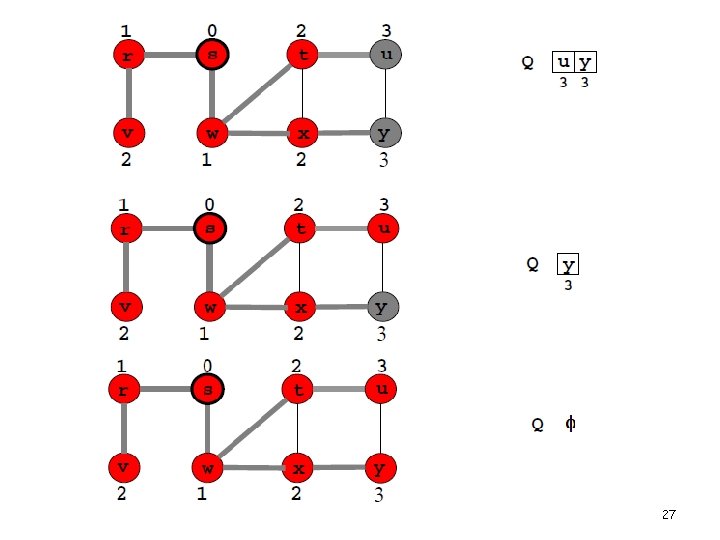
27

BFS - Running Time Adjacency list representation: 28

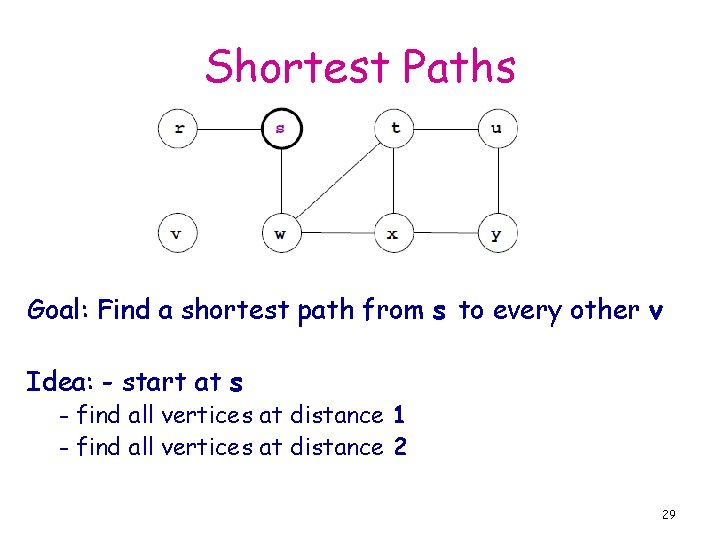
Shortest Paths Goal: Find a shortest path from s to every other v Idea: - start at s - find all vertices at distance 1 - find all vertices at distance 2 29

BFS for Shortest Paths 30

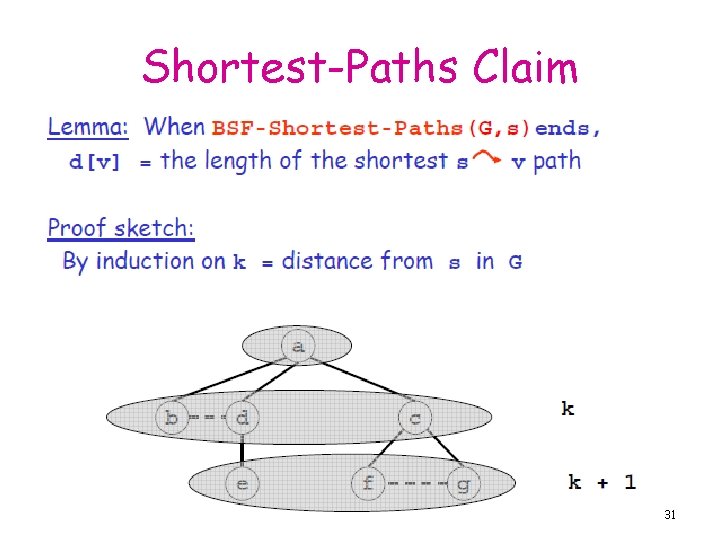
Shortest-Paths Claim 31

BFS for Connectivity 32

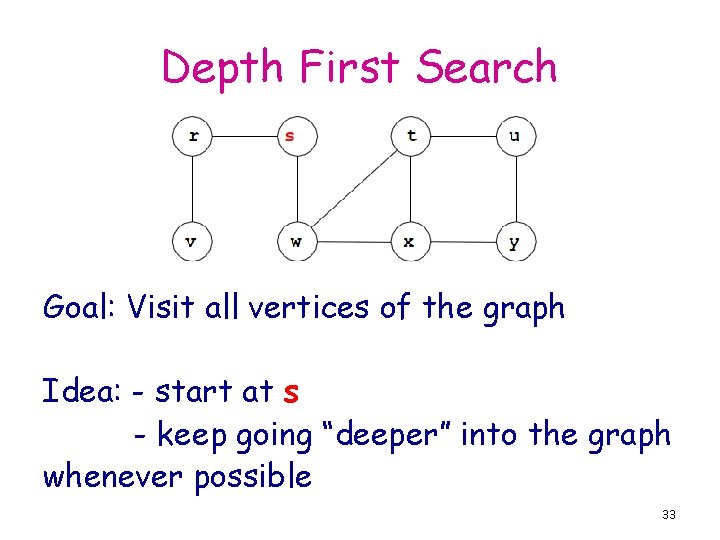
Depth First Search Goal: Visit all vertices of the graph Idea: - start at s - keep going “deeper” into the graph whenever possible 33

Depth First Search 34

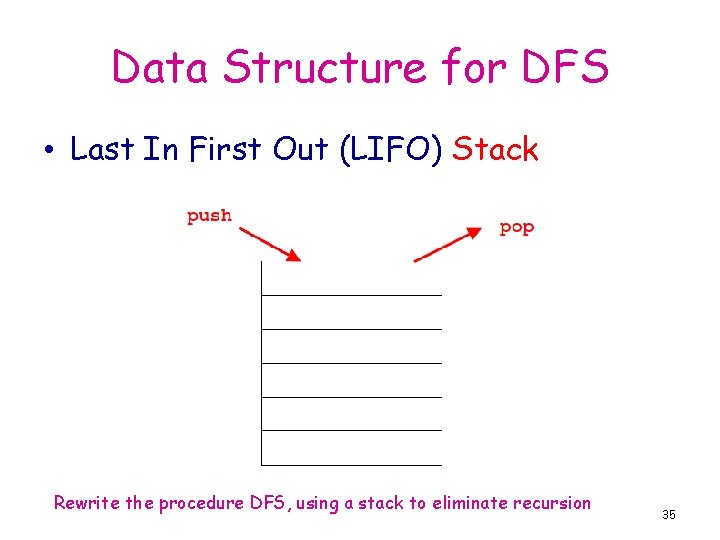
Data Structure for DFS • Last In First Out (LIFO) Stack Rewrite the procedure DFS, using a stack to eliminate recursion 35

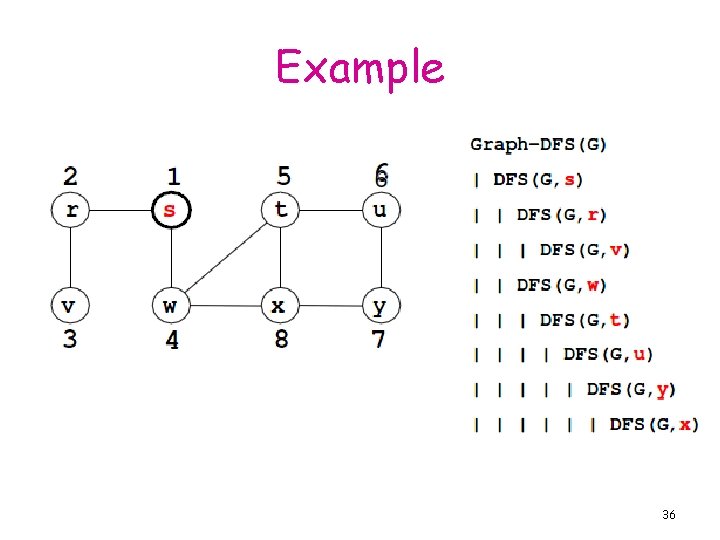
Example 36

Time Stamping 37

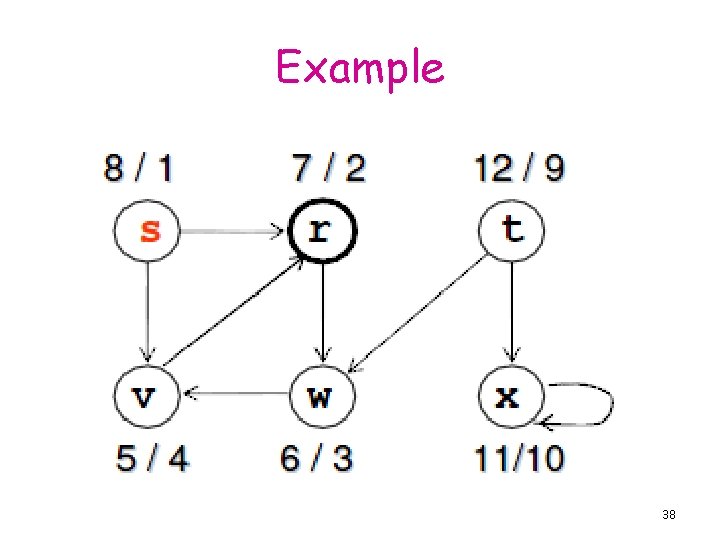
Example 38

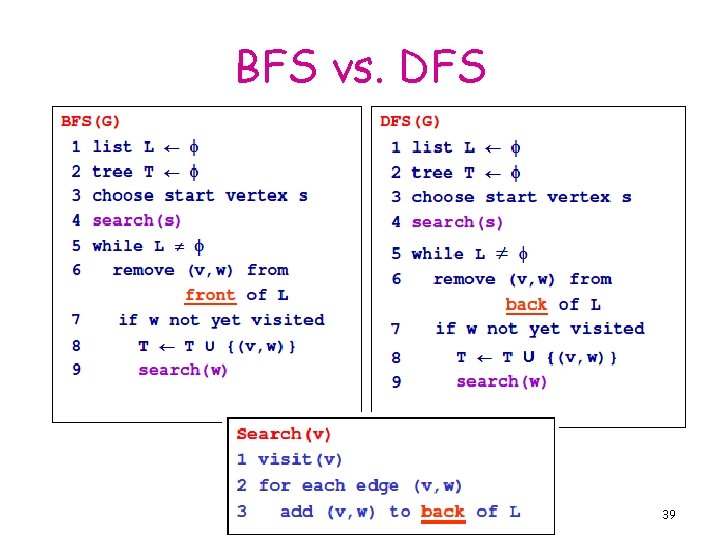
BFS vs. DFS 39

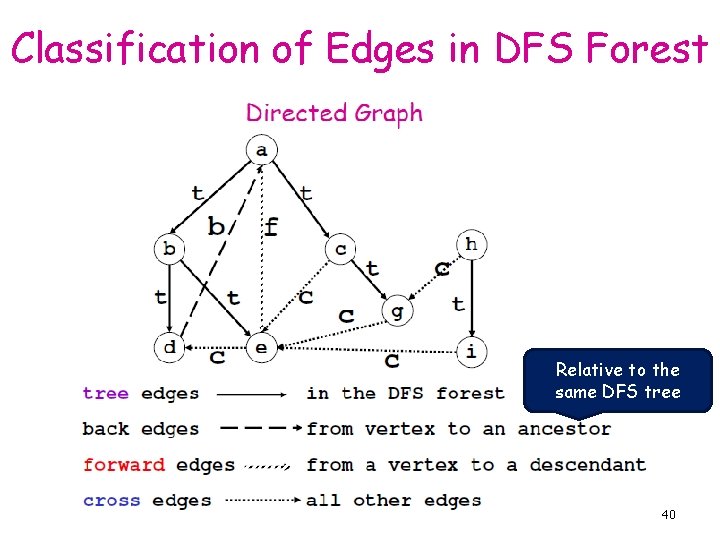
Classification of Edges in DFS Forest Relative to the same DFS tree 40

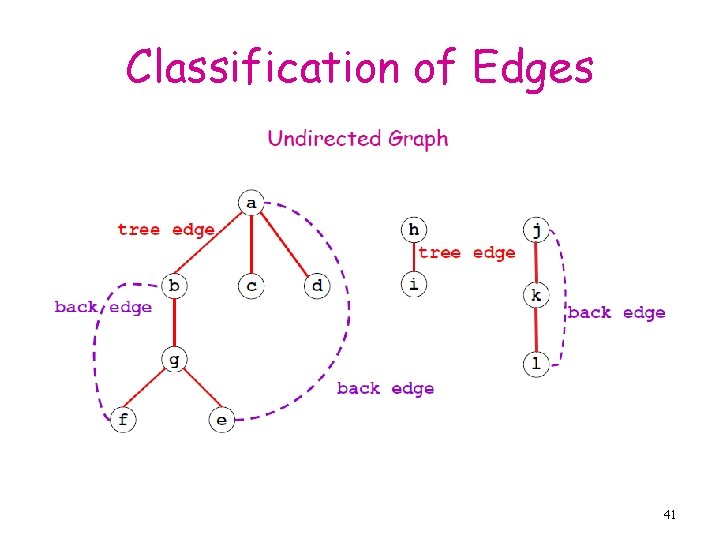
Classification of Edges 41

DFS - Running Time Adjacency list representation 42

Applications of DFS • 43

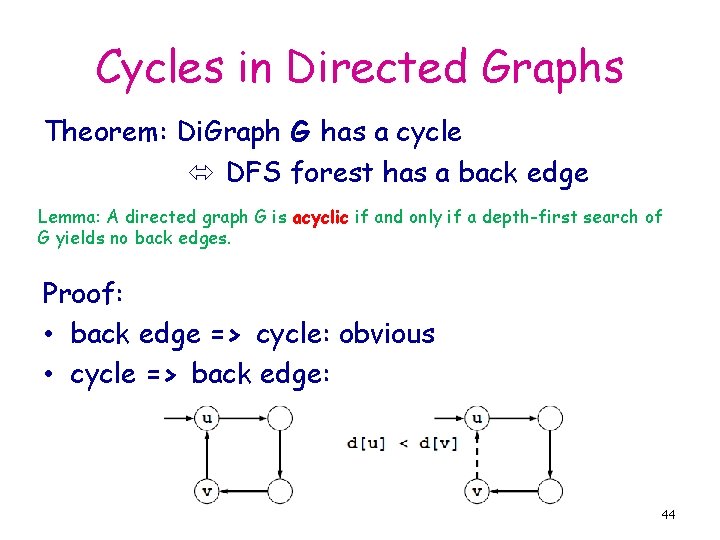
Cycles in Directed Graphs Theorem: Di. Graph G has a cycle DFS forest has a back edge Lemma: A directed graph G is acyclic if and only if a depth-first search of G yields no back edges. Proof: • back edge => cycle: obvious • cycle => back edge: 44

Topological Sort an ordering "<" of V[G] such that if (u, v) E[G] => u < v 45

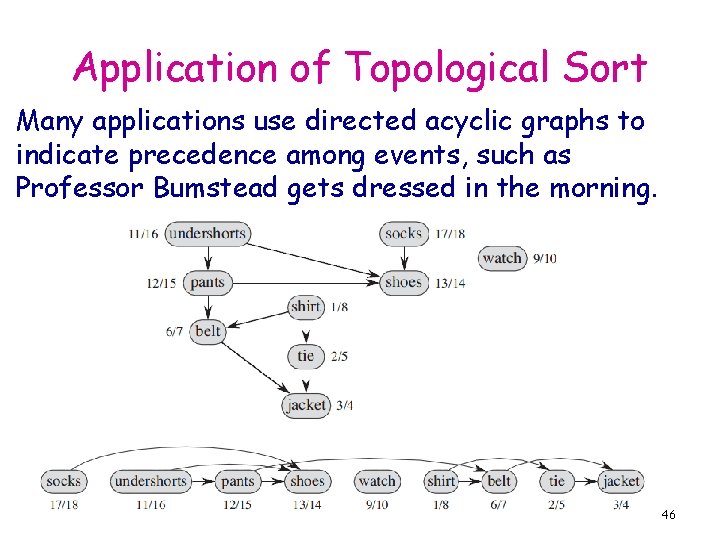
Application of Topological Sort Many applications use directed acyclic graphs to indicate precedence among events, such as Professor Bumstead gets dressed in the morning. 46

Topological Sort Lemma: G can be topologically sorted <=> G is a DAG (directed acyclic graph) Proof: cycle => G can't be sorted - obvious: no cycle => G can be sorted: we will show an algorithm 47

A Simple Top. Sort Algorithm Source = a vertex with indegree = 0 48

A Simple Top. Sort Algorithm Source = a vertex with indegree = 0 49

Adjacency Matrix Implementation 50

Adjacency List Implementation 51

Topological-Sort 1 call DFS. G/ to compute finishing times v. f for each vertex 2 as each vertex is finished, insert it onto the front of a linked list 3 return the linked list of vertices • 52

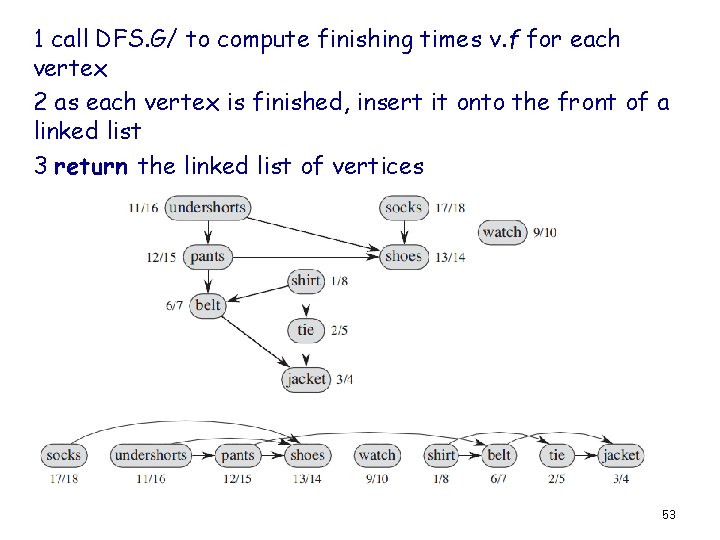
1 call DFS. G/ to compute finishing times v. f for each vertex 2 as each vertex is finished, insert it onto the front of a linked list 3 return the linked list of vertices 53

Graph in C++ • Boost/graph 54

Over 55

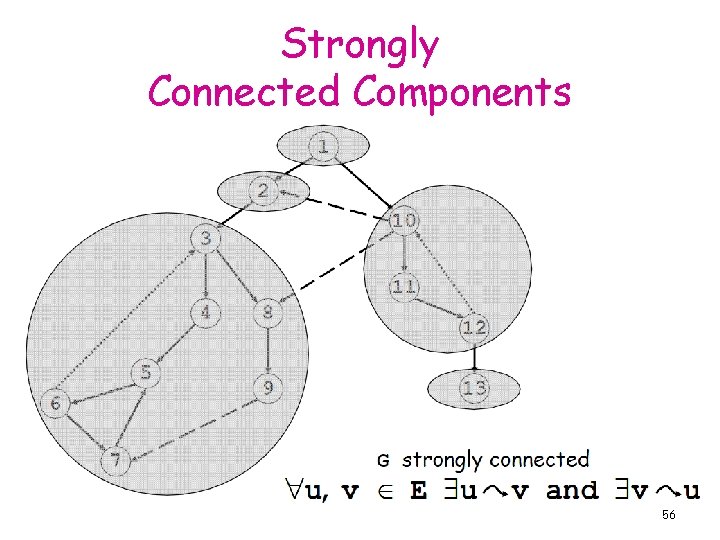
Strongly Connected Components 56

Simple SCC Algorithms 57