Data Representation Winter 2013 COMP 2130 Intro Computer

Data Representation Winter 2013 COMP 2130 Intro Computer Systems Computing Science Thompson Rivers University

Course Objectives n The better knowledge of computer systems, the better programing. Computer System C Programming Language Computer architecture CPU (Central Processing Unit) IA 32 assembly language Introduction to C language Physical main memory MMU (Memory Management Unit) Virtual memory space Memory hierarchy Cache Dynamic memory management Compiling, linking, loading, executing Better coding – locality Reliable and efficient programming for power programmers (to avoid strange errors, to optimize codes, to avoid security holes, …) TRU-COMP 2130 Data Representation 2

Course Contents n n n n n Introduction to computer systems: B&O 1 Introduction to C programming: K&R 1 – 4 Data representations: B&O 2. 1 – 2. 4 C: advanced topics: K&R 5. 1 – 5. 10, 6 – 7 Introduction to IA 32 (Intel Architecture 32): B&O 3. 1 – 3. 8, 3. 13 Compiling, linking, loading, and executing: B&O 7 (except 7. 12) Dynamic memory management – Heap: B&O 9. 9. 1 – 9. 9. 2, 9. 9. 4 – 9. 9. 5, 9. 11 Code optimization: B&O 5. 1 – 5. 6, 5. 13 Memory hierarchy, locality, caching: B&O 5. 12, 6. 1 – 6. 3, 6. 4. 1 – 6. 4. 2, 6. 5, 6. 6. 2 – 6. 6. 3, 6. 7 Virtual memory (if time permits): B&O 9. 4 – 9. 5 TRU-COMP 2130 Data Representation 3

Unit Learning Objectives n n n Convert a decimal number to binary number. Convert a decimal number to hexadecimal number. Convert a binary number to hexadecimal number. Convert a hexadecimal number to binary number. Distinguish little endian byte order and big endian byte order. Compute binary addition. Compute binary subtraction using 2’s complement. Determine the 2’s complement representation of a signed integer. Understand the overflow of unsigned integers and signed integers. Trace and fix faulty code. TRU-COMP 2130 Data Representation 4

n n n n Add two binary numbers. Compute the 1’s complement of a binary number. Compute the 2’s complement of a binary number. Understand the 2’s complement representation for negative integers. Subtract a binary number by using the 2’s complement addition. Multiply two binary numbers. Use of left shift and right shift. Binary division TRU-COMP 2130 Data Representation 5

Unit Contents n n Information Storage Integer Representations Integer Arithmetic Floating Point TRU-COMP 2130 Data Representation 6

1. Information Storage n Virtual memory, address, and virtual address space n n Virtual address space is a conceptual image presented to the machine-level program. Partitioned into more manageable units to store the different program objects, i. e. , instructions, program data, and control information. The actual machine level program simply treats each program object as a block of bytes, and the program itself as a sequence of bytes. Example n n n int number = 28; 4 bytes, i. e. , 32 bits, will be allocated to the variable number. The decimal number 28 will be stored in the 32 bits? How? Binary number, not the decimal, 00000000 00011100 will be stored in the 32 bits. Do programmers have to convert 28 to it’s binary number? TRU-COMP 2130 Data Representation 7

The Decimal System n Uses 10 digits 0, 1, 2, . . . , 9. n Decimal expansion: n n n 83 = 8× 10 + 3 4728 = 4× 103 + 7× 102 + 2× 101 + 8× 100 84037 = ? ? ? 43. 087 = ? ? ? Do you know addition, subtraction, multiplication and division? n n 1234 + 435. 78 1234 – 435. 78 1234 × 435. 78 1234 / 435. 78 TRU-COMP 1380 Number Systems 8

The Binary System n n n In computer systems, the most basic memory unit is a bit that contains 0 and 1. The data unit of 8 bits is referred as a byte that is the basic memory unit used in main memories and hard disks. All data are represented by using binary numbers. Data types such as text, voice, image and video have no meaning in the data representation. 8 bits are usually used to express English alphabets. A collection of n bits has 2 n possible states. Is it true? E. g. , n n How many different numbers can you express using 2 bits? How many different numbers can you express using 4 bits? How many different numbers can you express using 8 bits? How many different numbers can you express using 32 bits? TRU-COMP 1380 Number Systems 9

n n How can we store integers (i. e. , positive numbers only) in a computer? E. g. , n n A decimal number 329? Is it okay to store 3 characters ‘ 3’, ‘ 2’, and ‘ 9’ for 329? How are characters stored? 32910 = ? ? ? 2 TRU-COMP 1380 Number Systems 10

n n n Uses two digits 0 and 1. 02 12 102 112 1002 1012 1102 1112 10002 10012 = = = = = 0× 20 1× 21 1× 22 1× 23 = = + + + + 0× 20 1× 20 0× 21 1× 21 0× 22 How to expand binary numbers? = = + + + 0× 20 1× 20 0× 21 = = + 0× 20 = + 1× 20 = 010 110 210 310 410 510 610 710 810 910 . . . TRU-COMP 1380 Number Systems 11

n n n n Powers of 2 12 1002 10002 1 00002 100 00002 TRU-COMP 1380 = = = = 1× 20 1× 21 1× 22 1× 23 = + 0× 20 = + 0× 21 + 0× 20 = + 0× 22 + 0× 21 + 0× 20 = Number Systems 110 210 410 810 1610 3210 6410 12

n 1000 0000 00002 00002 = = = n 1 10 1000 1 0000 n Can you memorize the above powers of 2? n n n n ? ? ? 10 ? ? ? 10 Converting to decimals 11012 = ? ? ? 10 1011 00102 = ? ? ? 10 1011. 00102 = ? ? ? 10 TRU-COMP 1380 Number Systems 13

Converting Decimal to Binary n n n Quotient 10 5 2 1 0 21 / 2 10 / 2 5/2 2/2 1/2 => 2110 = 1 01012 Remainder 1 0 1 27110 = ? ? ? 2 607110 = ? ? ? 2 TRU-COMP 1380 Number Systems 14

n n Another similar idea 27110 = ? ? ? 2 256 < 271 < 512 8< 15 < 16 => 271 n -> 271 = 256 + 15 = 1 00002 + 15 -> 15 = 8 + 7 = 10002 + 7 = 1 00002 + 15 = 1 00002 + 10002 + 7 = 1 00002 + 10002 + 1112 = 1 0000 11112 127110 = ? ? ? 2 TRU-COMP 1380 Number Systems 15

Hexadecimal Number System n n n n n 010 = 00002 = 016 = 0 x 0 110 = 00012 = 116 = 0 x 1 210 = 00102 = 216 = 0 x 2 310 = 00112 = 316 = 0 x 3 410 = 01002 = 416 = 0 x 4 510 = 01012 = 516 = 0 x 5 610 = 01102 = 616 = 0 x 6 710 = 01112 = 716 = 0 x 7 810 = 10002 = 816 = 0 x 8 910 = 10012 = 916 = 0 x 9 1010 = 10102 = A 16 = 0 x. A 1110 = 10112 = B 16 = 0 x. B 1210 = 11002 = C 16 = 0 x. C 1310 = 11012 = D 16 = 0 x. D 1410 = 11102 = E 16 = 0 x. E 1510 = 11112 = F 16 = 0 x. F 14816 = ? ? ? 10 23 c 9 d 6 ef = ? ? ? 10 TRU-COMP 1380 4 bits can be used for a hexadecimal number, 0, . . . , F. Please memorize it! 14816 = ? ? ? 2 23 c 9 d 6 ef = ? ? ? 2 Number Systems 16

Converting Decimal to Hexadecimal n Quotient 20 × 16 + 1 × 16 + 0 × 16 + 328 / 16 = 20 / 16 = 1 / 16 = => 32810 = 14816 = ? ? ? 2 Remainder 8 4 1 n 14816 = (1 × 162 + 4 × 161 + 8 × 160)10 n 19210 = ? ? ? 16 TRU-COMP 1380 Number Systems 17

Converting Binary to Hexadecimal n n 4 DA 916 = ? ? ? 2 1001101101010012 = ? ? ? 16 = 100 1101 1010 1001 = 4 DA 9 10 11102 = 0 x? ? ? = ? ? ? 10 0100 1110 1011 1001 01002 = 0 x? ? ? = ? ? ? 10 TRU-COMP 1380 Number Systems 18

n Format specifiers in printf() for hexadecimal and decimal numbers? for (i = 0; i < num; i++) printf(“%d = 0 x%xn”, data[i]); n n But there is no printf format specifier to print an integer in the binary form. Write a function to make a string of 0’s and 1’s for a given integer. TRU-COMP 2130 Data Representation 19

Words n n A word size – the nominal size of integer and pointer data. A pointer variable contains an address in the virtual address space. We will discuss pointer variable in the next unit. The word size determines the maximum size of the virtual address space. n n 32 bit operating systems? 64 bit operating systems? TRU-COMP 2130 Data Representation 20

Data Sizes n printf(“%lun”, sizeof(long)); C data type 32 -bit 64 -bit char 1 1 short 2 2 int 4 4 long 4 8 long 8 8 char* 4 8 float 4 4 double 8 8 TRU-COMP 2130 //lu: long unsigned // integer Data Representation 21

Addressing and Byte Ordering n A variable x of type int n n n Address of x: 0 x 100 This means the 4 bytes of x would be stored in memory locations 0 x 100, 0 x 101, 0 x 102, and 0 x 103. How to interpret the bytes in memory locations 0 x 100, 0 x 101, 0 x 102, and 0 x 103? Let’s assume x has 0 x 1234567. There are two conventions to store the values in the 4 consecutive byte memory locations. 0 x 01, 0 x 23, 0 x 45, and 0 x 67, or 0 x 67, 0 x 45, 0 x 23, and 0 x 01, depending on CPU architecture. Little endian byte order – Intel-compatible machines 0 x 103 0 x 102 0 x 101 0 x 100 0 x 01 0 x 23 0 x 45 0 x 67 address value Big endian byte order – machines from IBM and Sun Microsystems 0 x 103 0 x 67 TRU-COMP 2130 0 x 102 0 x 45 0 x 101 0 x 23 0 x 100 0 x 01 Data Representation 22

n n The byte orderings are totally invisible for most application programmers. Why are the byte orderings important? 1. 2. 3. Think of data exchange between two machines through a network. Assembly programming When type casting is used TRU-COMP 2130 Data Representation 23

Representing Strings n n n A string is encoded by an array of characters terminated by the null (having 0) character ‘’; The ASCII character set Unicode – Some libraries are available for C. TRU-COMP 2130 Data Representation 24

Representing Code n n Different machine types use different and incompatible instructions and encodings. Even identical processors running different OSes have differences in their coding conventions and hence are no binary compatible. TRU-COMP 2130 Data Representation 25

Comparison and Logical Operations n n Comparison operators ? ? ? Logical operators ? ? ? TRU-COMP 2130 Data Representation 26

Bit-Level Operations n ? ? ? n &, |, ~, ^, >>, << n >>: Logical right shift and arithmetic right shift. n n n Logical right shit for unsigned integers: filled with 0 Arithmetic right shit for signed integers: filled with the MSB Examples char x = -128; unsigned char y = 128; x = x >> 1; y = y >> 1; printf (“%d, %dn”, x, y); n n We will discuss about this example later again. Some examples a x y ^ = = TRU-COMP 2130 a = 10; x ^ x ^ ? ? ? a ^ 0 = ? ? ? y = 20; y; y; y; Data Representation 27

n Some more examples 11110000 & 1100 = ? ? ? 11110000 | 1100 = ? ? ? 11110000 ^ 1100 = ? ? ? 0 x 3 B 0 x 33 n & 0 x 33 | 0 x 33 ^ 0 x 33 >> 2 = << 2 = = ? ? ? ? ? Consult with programming assignments TRU-COMP 2130 Data Representation 28

2. Integer Representations C Java char, unsigned char short, unsigned short byte 1 B short 2 Bs char in Java uses 2 Bs. int 4 Bs long 8 Bs // there is no unsigned in Java int, unsigned int long, unsigned long float double TRU-COMP 2130 float double Data Representation Size 4 Bs 8 Bs 29

Unsigned Encodings n unsigned char n n n n 32 bits The smallest number is ? ? ? The maximum number is ? ? ? unsigned long n 16 bits The smallest number is ? ? ? The maximum number is ? ? ? unsigned int n n The smallest number is 0 The maximum number is 0 xff. unsigned short n All 8 bits are used. No sign bit. 64 bits The smallest number is ? ? ? The maximum number is ? ? ? TRU-COMP 1380 Data Representations 30

Representation of Unsigned Integers n 8 -bit representation of unsigned char 255 254. . . 128 127 126. . . 2 1 0 n n 11111110. . . 10000000 01111111 01111110. . . 00000010 00000001 0000 +1 +1 +1 overflow The maximum number is ? The minimum number is ? What if we add the maximum number by 1 ? ? ? What if we subtract the minimum number by 1 ? ? ? TRU-COMP 1380 Data Representations 31

unsigned char x, y; x = 128; y = 128; printf(“x = %d, y = %dn”, x, y); printf(“x + y = %dn”, x + y); // int (not char) addition x = x + y; // 256 -> 10000 -> truncation printf(“x = %d, y = %dn”, x, y); X = 128; x = x >> 1; // logical right shift for unsigned printf(“x = %dn”, x); n The output is ? ? ? n 128, 128 256 0, 128 64 n 16 -bit, 32 -bit, 64 -bit representations have the same overflow problem. n How to represent signed integers? TRU-COMP 2130 Data Representation 32

Binary Addition n n We will discuss binary addition and binary subtraction, before we discuss the representation of signed integers. How to add two binary numbers? Let’s consider only unsigned integers (i. e. , positive numbers only) for a while. Just like the addition of two decimal numbers. carry E. g. , 10010 1111 + 1001 + 1011 + 1 11011 11101 ? ? ? + TRU-COMP 1380 10111 ? ? ? Data Representations 33

Binary Subtraction n How to subtract a binary number? Just like the subtraction of decimal numbers. E. g. , 0112 02 02 1000 10 10 10010 -1 -1 -11 1 ? 11 Try: 101010 -101 TRU-COMP 1380 How to do? Data Representations 10010 -11 1111 1 -10 34

n n n In the previous slide, 10010 – 11 = 1111 What if we add 00010010 + 11111100 1 00001110 + 1 00001111 Is there any relationship between 112 and 111002? The 1’s complement of 112 is ? ? ? Switching 0 1 This type of addition is called 1’s complement addition. Find the 8 -bit one’s complements of the followings. n n n 11011 -> 00011011 -> 10 -> 00000010 -> 101 -> 00000101 -> TRU-COMP 1380 Data Representations 35

n n In the previous slide, 10010 – 11 = 1111 What if we add 00010010 + 11111101 1 00001111 Is there any relationship between 11 and 11101? The 2’s complement of 11 is ? ? ? n n n 2’s complement ≡ 1’s complement + 1 -> 11100 + 1 = 11101 This type of addition is called 2’s complement addition. Find the 16 -bit two’s complements of the followings. n n n 11011 -> 00000011011 -> 10 101 TRU-COMP 1380 Data Representations 36

n Another example - 101010 101 ? ? ? n What if we use 1’s complement addition or 2’s complement addition instead as follow? Let’s use 8 -bit representation. + 1 + n 00101010 11111010 00100100 1 00100101 + 1 00101010 11111011 00100101 What does this mean? n n A – B = A + (–B), where A and B are positive Is the 1’s complement or the 2’s complement of B sort of equal to –B? TRU-COMP 1380 Data Representations 37

n Can we use 8 -bit 1’s complement addition for 12 – 102 = – 12 ? - 1 10 + 00000001 11111110 <- 8 -bit 1’s complement of 10 <- Is this correct? (1’s complement of 1? ) n Let’s use 8 -bit 2’s complement addition for 12 – 102. 00000001 + 11111110 1111 <- 2’s complement of 10 <- Correct? (2’s complement of 1? ) n 12 – 102 = 12 + (– 102) = – 12 n How to represent negative binary numbers, i. e. , signed integers? TRU-COMP 1380 Data Representations 38

Representation of Negative Binaries n n n Representation of signed integers 8 or 16 or 32 bits are usually used for integers. Let’s use 8 bits for examples. n n n How to represent positive integer 9? n n The left most bit (called most significant bit) is used as sign. When the MSB is 0, non-negative integers. When the MSB is 1, negative integers. The other 7 bits are used for integers. 00001001 How about -9? n n n 10001001 is really okay? 00001001 (9) + 10001001 (-9) = 10010010 (-18) It is wrong! We need a different representation for negative integers. TRU-COMP 1380 Data Representations 39

n How about -9? n n What is the 8 -bit 1’s complement of 9? n n n 11110110 00001001 + 11110110 = 1111 <- 8 -bit 1’s complement of 9 <- 9 + 8 -bit 1’s complement of 9 <- Is it zero? (1’s complement of 0? ) What is the 2’s complement of 9? n n n 10001001 is really okay? 00001001 (9) + 10001001 (-9) = 10010010 (-18) It is wrong! We need a different representation for negative integers. 11110111 00001001 + 11110111 = 1 0000 <- 8 -bit 2’s complement of 9 <- 9 + 8 -bit 2’s complement of 9 <- It looks like zero. 2’s complement representation is used for negative integers. TRU-COMP 1380 Data Representations 40

n n n n 12 – 102 = 12 + (– 102) ? ? ? What is the result in decimal? 00000001 + 11111110 <- 2’s complement of 10, i. e. , -102 1111 <- 2’s complement of 1, i. e. , -1 (= 1 – 2) 1010102 – 1012 = 1010102 + (– 1012) ? ? ? 100102 – 112 ? ? ? 102 – 12 ? ? ? -102 – 12 ? ? ? Is the two’s complement of an integer the same integer? What is x when the 8 -bit 2’s complement of x is n 1111 TRU-COMP 1380 11110011 Data Representations 10000001 41

n n n 8 -bit representation of signed char with 2’s complement 127 01111111 126 01111110 overflow. . . 2 00000010 1 00000001 0 0000 -1 1111 -2 11111110 -3 11111101. . . +1 -127 10000001 -1 +1 -128 10000000 -1 -1 The maximum number is ? The minimum number is ? What if we add the maximum number by 1 ? ? ? What if we subtract the minimum number by 1 ? ? ? TRU-COMP 1380 Data Representations +1 overflow 42

n 16 -bit representation signed short with 2’s complement overflow. . 3 2 1 0 -1 -2 -3. . n n 01111111 11111110. . . 00000011 00000010 00000001 00000000 11111111 11111110 11111101. . . 100000001 10000000 +1 +1 +1 overflow -1 -1 -1 The maximum number is ? What if we add the maximum number by 1 ? ? ? The minimum number is ? What if we subtract the minimum number by 1 ? ? ? TRU-COMP 1380 Data Representations 43

n n Note that computers use the 8 -bit representation, the 16 -bit representation, the 32 -bit representation and the 64 -bit representation with 2’complement for negative integers. In programming languages n n n char, short, int, long, unsigned char unsigned short unsigned int unsigned long 8 -bits 16 -bits 32 -bits 64 -bits When we use the 32 -bit representation with 2’s complement, n n The maximum number is ? What if we add the maximum number by 1 ? ? ? The minimum number is ? What if we subtract the minimum number by 1 ? ? ? TRU-COMP 1380 Data Representations 44

n n n Now we know how to represent negative integers. 2’ complement addtion A + (–B) is computed for subtraction A – B. Let’s suppose B is negative. Then –B is really a positive integer? For example, let’s consider 1 byte signed integer. 127 126. . . 2 1 0 -1 -2 -3. . . -127 -128 n 01111111 01111110. . . 00000010 00000001 0000 11111110 11111101. . . 10000001 10000000 2’s complement of -3 is 00000011, i. e. , 3. 2’s complement of -128 is 10000000 again. For any -127 < x < 127, x – x = 0. But (-128) – (-128) = ? ? ? TRU-COMP 2130 Data Representation 45

char x, y; x = 128; // 128 -> 10000000 This is -128. y = 128; printf(“x = %d, y = %dn”, x, y); printf(“x – y = %dn”, x - y); x = x – y; printf(“x = %d, y = %dn”, x, y); x = 128; x = x >> 1; // arithmetic shift for signed printf(“x = %dn”, x); n The output is ? ? ? n n -128, -128 0 0, -128 -64 -128 – (-128) = -128 + (-(-128)) = -128 + (-128) = 10000000 + 10000000 = 0 TRU-COMP 2130 Data Representation 46

char a = 127, b = 127, c; unsigned char d; c = a + b; d = a + b; printf(“a=%d, b=%d, c=%d, d=%dn”, a, b, c, d); n The output is ? ? ? n a=127, b=127, c=-2, d=254 01111111 + 01111111 = 11111110 ? ? ? n We have to be very careful with overflow for integer values. TRU-COMP 2130 Data Representation 47

Advice on Signed vs. Unsigned n Practice Problem 2. 25 float sum_elements (float a[], unsigned int length) { int i; float result = 0; for (i = 0; i <= length-1; i++) result += a[i]; return result; } n When run with length equal to 0, this code should return 0. 0. Instead it encounters a memory error. Why? ? ? n n unsigned int length-1 How to fix this code? TRU-COMP 2130 Data Representations 48

short unsigned short x = -5; y = 128; printf(“%x, %xn”, x, y); printf(“%x, %x, %xn”, x<<3, x>>3, y<<3, y>>3); The output is ? ? ? fffffffb, 80 n Singed integers: n n ffffffd 8, ffff, 400, 10 Arithmetic right shift: Left part is filled with the most significant bit of the original value. Unsigned integers: n Logical right shift: Left part is filled with 0. TRU-COMP 2130 Data Representations 49

n Practice Problem 2. 26 size_t strlen(const char* s); // defined in string. h int strlonger(char s[], char t[]) { return strlen(s) – strlen(t) > 0; } Note that size_t is defined in stdio. h to be unsigned int. n For what cases will this function produce an incorrect result? n n -> 1 (true value) Explain how this incorrect result comes about. n n 0– 1>0 Unsigned int of 0 – 1 is 0 xffff that is greater than 0. Show to fix the code so that it will work reliably. TRU-COMP 2130 Data Representations 50

Conversions Between Signed and Unsigned short v = -12345; unsigned short uv = (unsigned short)v; printf(“v=%x, v=%d, uv=%x, uv=%un”, v, v, uv); n The output is v=ffffcfc 7, v=-12345, uv=cfc 7, uv=53191 (12*163+15*162+12*16+7) n What if we convert an unsigned integer to signed integer? short v = -12345, w; unsigned short uv = v; // implicit type casting w = uv; printf(“v = %d, uv = %u, w = %dn”, v, uv, w); n The output is v = -12345, uv = 53191, w = -12345 TRU-COMP 2130 Data Representation 51

Truncating Numbers int x = 53191; // 0 xcfc 7: 0. . . 0 11001111 11000111 short sx = (short)x; // -12345 int y = sx; // ? ? ? printf(“x = %d, sx = %d, y = %dn”, x, sx, y); char a = 128, b = 128; x = a + b; // int (not short) addition y = a – b; // int (not short) subtraction printf(“%d, %d, %dn”, a, b, x, y); n The output is ? ? ? n 53191, -12345 TRU-COMP 2130 -128, -256, 0 Data Representation 52

3. Integer Arithmetic n What we have discussed n n Unsigned addition Two’s complement negation Overflow problems TRU-COMP 2130 Data Representation 53

Unsigned Multiplication n E. g. , n n n Unsigned multiplication n n 1001101 × 1 = ? ? ? 1001101 × 100 = ? ? ? 1001101 × 101 = 1001101 × 10 + 1001101 × 1 = 100110100 + 1001101 = 110000001 x y mod 2 w -> truncation of the bits above w bits Two’s complement multiplication for signed integers n U 2 Tw(x y mod 2 w), where U 2 T means unsigned to two’s complement TRU-COMP 2130 Data Representation 54

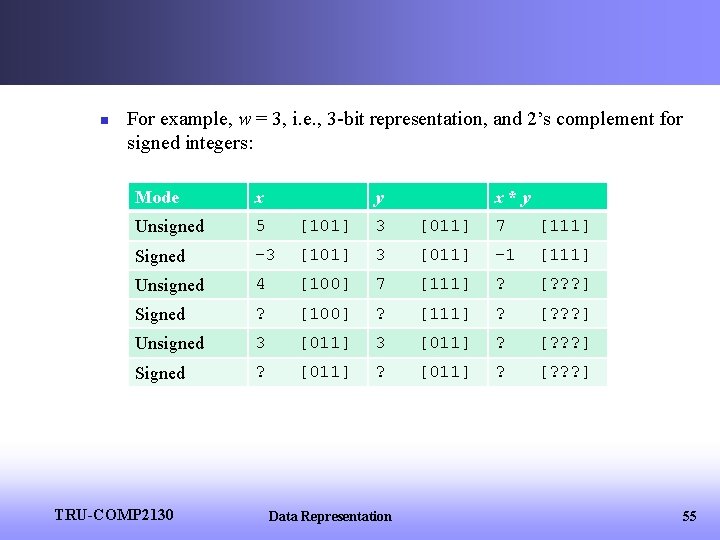
n For example, w = 3, i. e. , 3 -bit representation, and 2’s complement for signed integers: Mode x Unsigned 5 [101] 3 [011] 7 [111] Signed -3 [101] 3 [011] -1 [111] Unsigned 4 [100] 7 [111] ? [? ? ? ] Signed ? [100] ? [111] ? [? ? ? ] Unsigned 3 [011] ? [? ? ? ] Signed ? [011] ? [? ? ? ] TRU-COMP 2130 y Data Representation x*y 55

Multiplying by Constants n n n What if we shift 1001 left by one bit? 1001 -> 10010 9 -> ? ? What if we shift 1001 left by two bits? 1001 -> 100100 9 -> ? ? Multiplication by a power of 2. TRU-COMP 2130 Data Representation 56

Dividing by Powers of Two n n What if we shift 100100 right by one bit? 00100100 -> 00010010 ? ? -> ? What if we shift 100100 right by two bits? 00100100 -> 00001001 ? ? -> ? Division by a power of 2. Need to think logical right shift for unsigned integers as shown in the above example, and arithmetic right shift for signed integers. TRU-COMP 2130 Data Representation 57

n Binary division? 101 n n 1111 1001101 -101 1000 -101 111 -101 10 <- quotient This is why division is an expensive operation. <- remainder Try 1101011 / 110 Dividing negative binary numbers: division without sign, and then put the sign. TRU-COMP 1380 Number Systems 58

n Binary division by a power of 2? 1001101 / 10 = 1001101 / 1000 = 1001 n What if we shift 1001101 right by 1 bit? What if we shift 1001101 right by 2 bits? What if we shift 1001101 right by 3 bits? n 1001101 / 101 ? ? ? n n TRU-COMP 1380 Number Systems Complicated implementation required 59

2. 4 Floating Point n n Fractional binary numbers IEEE floating-point representation TRU-COMP 2130 Data Representation 60

Fractions: Fixed-Point n How can we represent fractions? n n Use “binary point” to separate positive from negative powers of two -- like “decimal point. ” 2’s comp addition and subtraction still work. (Assuming binary points are aligned) 2 -1 = 0. 5 2 -2 = 0. 25 2 -3 = 0. 125 00101000. 101 (40. 625) + 11111110. 110 (-1. 25) (2’s complement) 00100111. 011 (39. 375) No new operations -- same as integer arithmetic. TRU-COMP 1380 Number Systems 61

n Just for your curiosity: How to convert decimal fractions to binary? n 0. 62510 = ? ? ? 2 n n n 0. 625 * 2 = 1. 25 -> 1 0. 25 * 2 = 0. 5 -> 0 0. 5 * 2 = 1. 0 -> 1 Therefore 0. 101 (0. 625 = x 2 -1 + y 2 -2 + z 2 -3 +. . . ) (1. 25 = x + y 2 -1 + z 2 -2 +. . . => x = 1) (0. 25 = y 2 -1 + z 2 -2 +. . . ) 0. 710 = ? ? ? 2 n n n n n TRU-COMP 1380 0. 7 * 2 = 1. 4 -> 1 0. 4 * 2 = 0. 8 -> 0 0. 8 * 2 = 1. 6 -> 1 0. 6 * 2 = 1. 2 -> 1 0. 2 * 2 = 0. 4 -> 0 0. 4 * 2 = 0. 8 -> 0 0. 8 * 2 = 1. 6 -> 1. . . Therefore 0. 1011001. . . Number Systems How to deal with big numbers and small numbers? 62

Very Large and Very Small: Floating-Point n n Large values: 6. 023 × 1023 -- requires 79 bits Small values: 6. 626 × 10 -34 -- requires > 110 bits Use equivalent of “scientific notation”: F × 2 E Need to represent F (fraction), E (exponent), and sign. n n 6. 023 × 1023 = 0. 6023 × 1024 6. 626 × 10 -34 = 0. 6626 × 10 -33 00101000. 101 (40. 62510) = 0. 101000101 × 26. Store 6 in the exponent and 101000101 in mantissa. (Try the multiplication) IEEE 754 Floating-Point Standard (32 -bits): 1 b 8 bits 23 bits S TRU-COMP 1380 Exponent Fraction (mantissa) Number Systems 63

Floating Point in C n Two different floating-point data types n n n float double Type casting n n int -> float -> double -> float, double -> int TRU-COMP 1380 Number Systems The value may be rounded. The exact value can be preserved. The value may be rounded. The value will be rounded toward zero. E. g. , 1. 999 -> 1; -1. 999 -> -1 64