Data Representation numbers Binary conversion Hexadecimal Negative numbers

Data Representation – numbers Binary conversion Hexadecimal Negative numbers Binary addition Binary shifts

Basic Binary 1 = switch closed / electricity on 0 = switch open / electricity off If you send 1 bit, how many different combinations can you send? 1 or 0 If you send 2 bits, how many different combinations can you sent? 00 01 10 11 3 bits? 4 bits? 5 bits?

Terminology Bit 1 or 0 Nibble 4 bits Byte 2 nibbles / 8 bits KB Kilobyte 1000/1024 bytes MB Megabyte 1000/1024 KB GB Gigabyte 1000/1024 MB TB Terabyte 1000/1024 GB
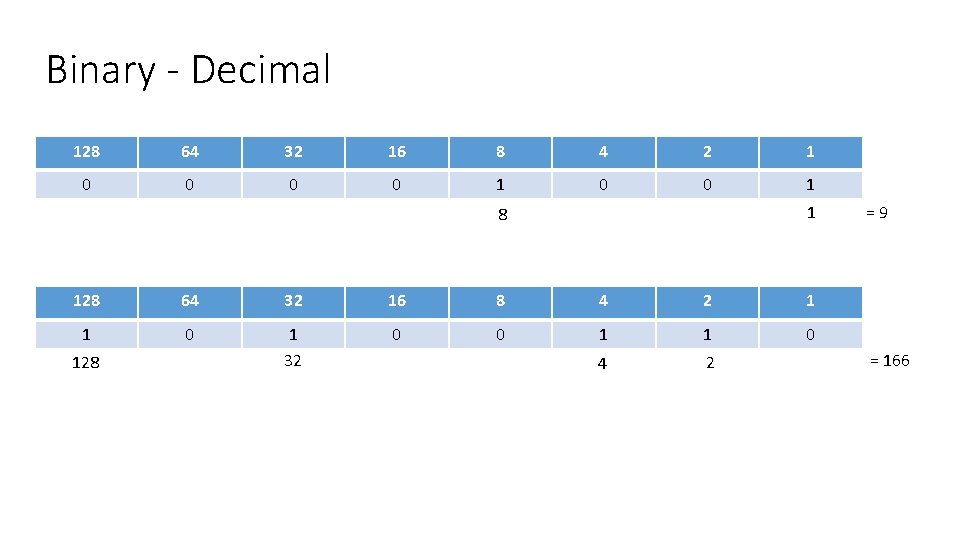
Binary - Decimal 128 64 32 16 8 4 2 1 0 0 1 1 8 128 64 32 16 8 4 2 1 1 0 1 32 0 0 1 1 0 4 2 128 =9 = 166
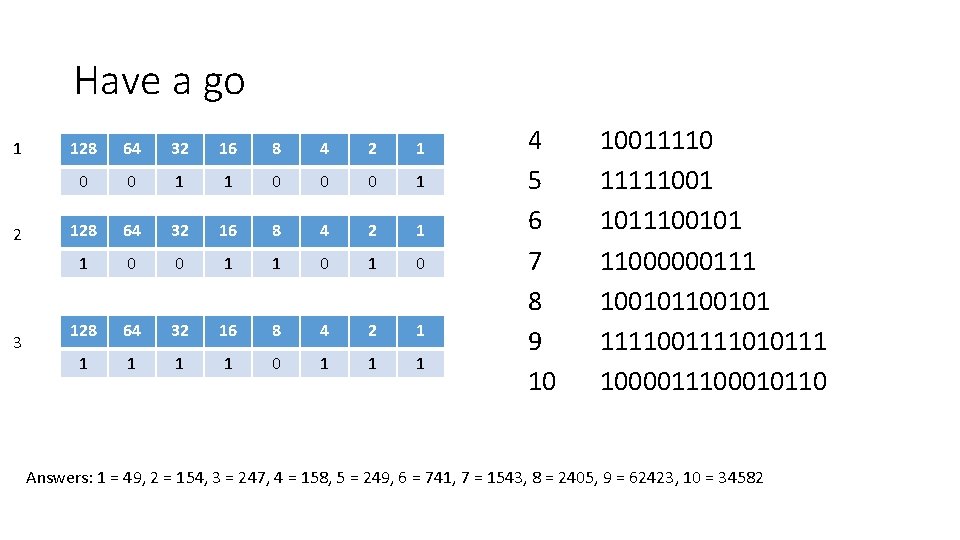
Have a go 1 2 3 128 64 32 16 8 4 2 1 0 0 1 1 0 0 0 1 128 64 32 16 8 4 2 1 1 0 0 1 1 0 128 64 32 16 8 4 2 1 1 1 0 1 1 1 4 5 6 7 8 9 10 10011110 11111001 1011100101 11000000111 100101 1111001111010111 1000011100010110 Answers: 1 = 49, 2 = 154, 3 = 247, 4 = 158, 5 = 249, 6 = 741, 7 = 1543, 8 = 2405, 9 = 62423, 10 = 34582

Patterns • If the least significant bit (right most) is a 1, the number is odd • All 1 s = the next number -1 e. g. 128 64 32 16 8 4 2 1 0 1 1 1 1 = 127 • The smallest number in positive binary is always 0 • The number of combinations is equal to the next number e. g. 128 64 32 16 8 4 2 1 0 1 1 1 1 = 128 different combinations 0 to 127
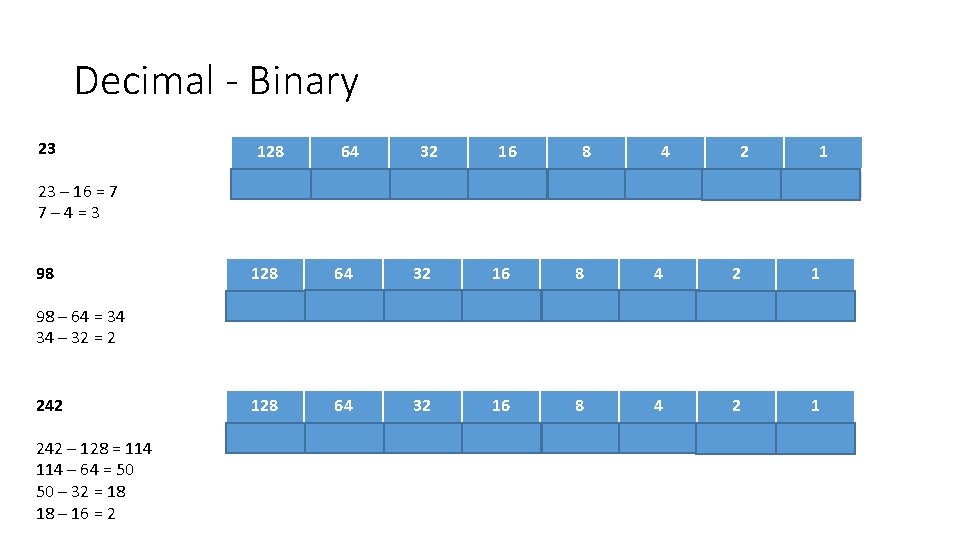
Decimal - Binary 23 23 – 16 = 7 7– 4=3 98 98 – 64 = 34 34 – 32 = 2 242 – 128 = 114 – 64 = 50 50 – 32 = 18 18 – 16 = 2 128 64 32 16 8 4 2 1 0 0 0 1 1 1 128 64 32 16 8 4 2 1 0 1 1 0 0 0 128 64 32 16 8 4 2 1 1 1 0 0 1 0

Have a go 1 2 3 4 5 28 43 78 101 200 6 7 8 9 10 220 269 612 2974 32651 Answers: 1 = 11100, 2 = 101011, 3 = 1001110, 4 = 1100101, 5 = 11001000, 6 = 11011100, 7 = 100001101, 8 = 100100, 9 = 101110011110, 10 = 11110001011

Hexadecimal • Easier to remember than binary • Quicker/easier to write than binary • Can be converted quickly to binary (and back) • Each nibble is converted into a single hexadecimal number 1 nibble can be: Decimal Hexadecimal 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 A 11 B 12 C 13 D 14 E 15 F
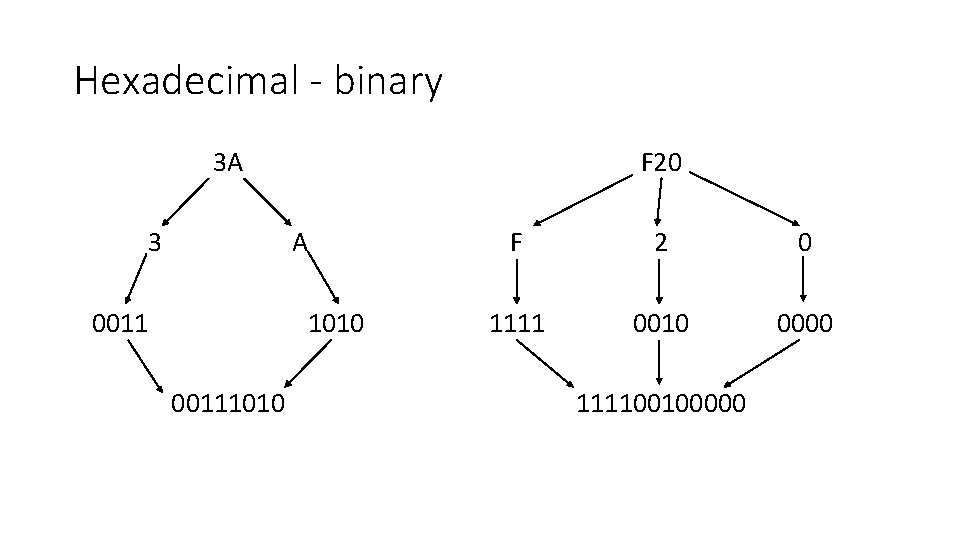
Hexadecimal - binary 3 A 3 F 20 A 0011 1010 00111010 F 2 0 1111 0010 0000 111100100000

Have a go, hex-bin 1 2 3 4 5 11 2 A BB 6 C A 0 6 7 8 9 10 50 F 9 BD D 5 AA 1974 26 ABEB Answers: 1 = 0001, 2 = 00101010, 3 = 1011, 4 = 01101100, 5 = 10100000, 6 = 010100001111, 7 = 100110111101, 8 = 110101010, 9 = 0001100101110100, 10 = 00100110101111101011
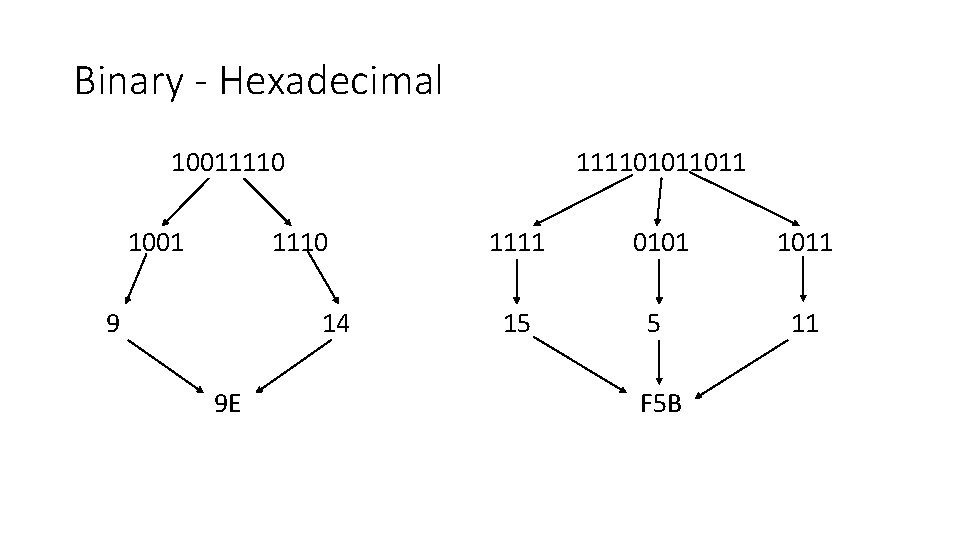
Binary - Hexadecimal 10011110 1001 111101011011 1110 9 14 9 E 1111 0101 1011 15 5 11 F 5 B

Have a go, binary-hex 1 2 3 4 5 01100001 10111111 10000000 01011111 111001101011 6 7 8 9 10 00101100 11110000111111 0101111000101011 111100010110 Answers: 1 = 6 A, 2 = BF, 3 = 80, 4 = 5 F, 5 = E 6 B, 6 = 2 AC, 7 = F 0 F, 8 = 33 F, 9 = 5 E 2 B, 10 = FF 16

Hexadecimal - Decimal 3 A = • Convert to binary and then to decimal… • Or… 162 161 16 160 3 A (3 * 16) + (10 * 1) = 58 160 1 D 3 = 256 161 1 162 161 160 1 D 3 (1 * 16 ) + (13 * 16) + (3 * 1) = 467

Have a go, hex-dec 1 2 3 4 5 11 2 A BB 6 C A 0 6 7 8 9 10 50 F 9 BD D 5 AA 1974 26 ABEB Answers: 1 = 17, 2 = 42, 3 = 187, 4 = 108, 5 = 160, 6 = 1295, 7 = 2493, 8 = 54698, 9 = 6516, 10 = 2534379

Decimal – Hexadecimal 78 • Convert the binary and then hexa • Or 199 256 16 1 0 12 7 299 256 16 1 1 11 162 161 160 256 16 1 0 4 14 2 = 4 E = C 7 = 12 B

Have a go – dec-hex 1 2 3 4 5 22 59 100 189 231 6 7 8 9 10 257 1056 2000 3578 32444 Answers: 1 = 16, 2 = 3 B, 3 = 64, 4 = BD, 5 = E 7, 6 = 101, 7 = 420, 8 = 7 D 0, 9 = DFA, 10 = 7 EBC
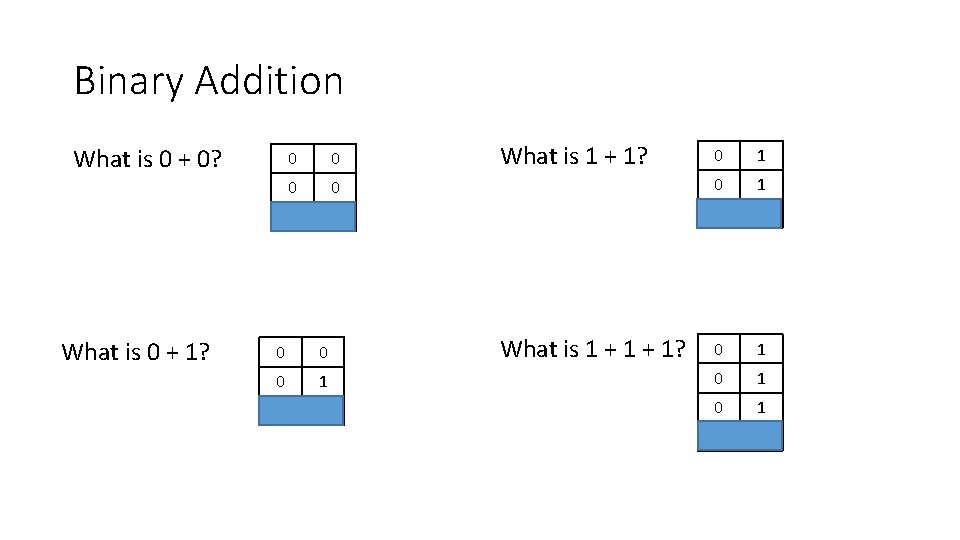
Binary Addition What is 0 + 0? What is 0 + 1? What is 1 + 1? 0 1 0 0 What is 1 + 1? 0 0 0 1 0 1 1 1
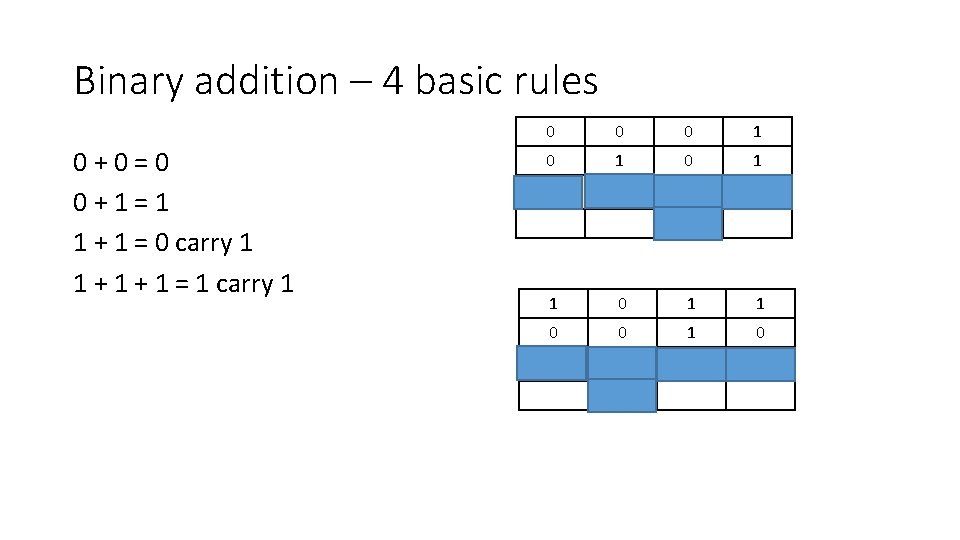
Binary addition – 4 basic rules 0+0=0 0+1=1 1 + 1 = 0 carry 1 1 + 1 = 1 carry 1 0 0 0 1 0 1 1 0 0 1 1
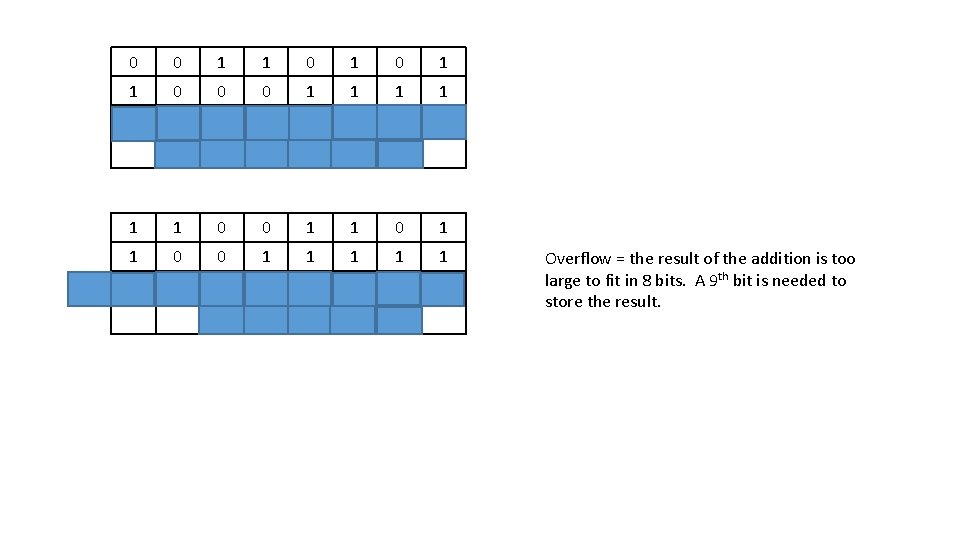
(1) 0 0 1 1 0 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 1 1 Overflow = the result of the addition is too large to fit in 8 bits. A 9 th bit is needed to store the result.

Have a go, binary addition 0 0 1 1 0 1 1 0 0 1 1 1 (1) (1) 1 1 0 0 1 1 1 0 0 0 1 1 0 1 0 1 0 1 0 0 1 1 (1) 1 0 0 1 0 1 0 1 1 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1 0 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1 1

Negative numbers – Sign and Magnitude The MSB bit (left most) gives the sign (it does not have a numeric value). 1 = negative, 0 = positive 0011 = 3 1011 = -3 01010 = 10 11010 = -10 Work out the binary – add a 0 or a 1 at the front

Have a go, dec – sign and mag 1 2 3 4 5 22 -33 59 -100 105 6 7 8 9 10 -106 -221 398 -512 -1069 Answers: 1 = 010110, 2 = 1100001, 3 = 0111011, 4 = 11100100, 5 = 01101001, 6 = 11101010, 7 = 11101, 8 = 0110001110, 9 = 1100000, 10 = 110000101101

Negative numbers – Two’s complement Dec – two’s Convert the number to binary as normal. Make sure there is a 0 in the MSB. If the decimal number is positive, you already have the answer. If it is negative, you need to flip it: Method 1: 1. Flip all the bits 2. Add 1 01011010 Flip: 10100101 Add 1: 10100110 Method 2: 1. Right to left write down all the bits up to and including the first 1. 2. Flip the rest 01011010 Keep same: 10 Flip the rest: 10100110

Dec-two’s examples 59 Convert to binary (with a 0 at the front): 0111011 59 is positive, so the answer is 0111011 -59 Convert to binary (with a 0 at the front): 0111011 Flip all the bits: 1000100 Add 1: 1000101

Have a go, Dec – two’s 1 2 3 4 5 22 -33 59 -100 105 6 7 8 9 10 -106 -221 398 -512 -1069 Answers: 1 = 010110, 2 = 0010, 3 = 0111011, 4 = 10011100, 5 = 01101001, 6 = 10010110, 7 = 00100011, 8 = 0110001110, 9 = 1100000, 10 = 101111010011

Two’s complement, two’s-dec Check the first bit. If it is a 0 – convert it to decimal as normal. If it is a 1, you need to flip it, then work it out as normal: Method 1: 1. Flip all the bits 2. Add 1 10011110 Flip: 01100001 Add 1: 01100010 Method 2: 1. Right to left write down all the bits up to and including the first 1. 2. Flip the rest 10011110 Keep same: 10 Flip the rest: 01100010

Two’s-dec examples 01011111 First bit = 0 so convert as normal = 95 10010100 First bit = 1 so flip and add 1 Flip: 01101011 Add 1: 01101100 Convert: -108

Have a go, Two’s – dec 1 2 3 4 5 00110101 10111010 11000000 01000110 0101 6 7 8 9 10 1010 11010 1110001110 011010101 111010101 Answers: 1 = 53, 2 = -70, 3 = -64, 4 = 70, 5 = 85, 6 = -86, 7 = -166, 8 = -114, 9 = 3413, 10 = -5419

Binary Shifts • Move binary numbers a set number of places to the left, or the right • Logical shift – spaces are filled in with 0 s • Arithmetic shift – when shifting left the spaces are filled with 0 s, when shifting right they are filled with the MSB
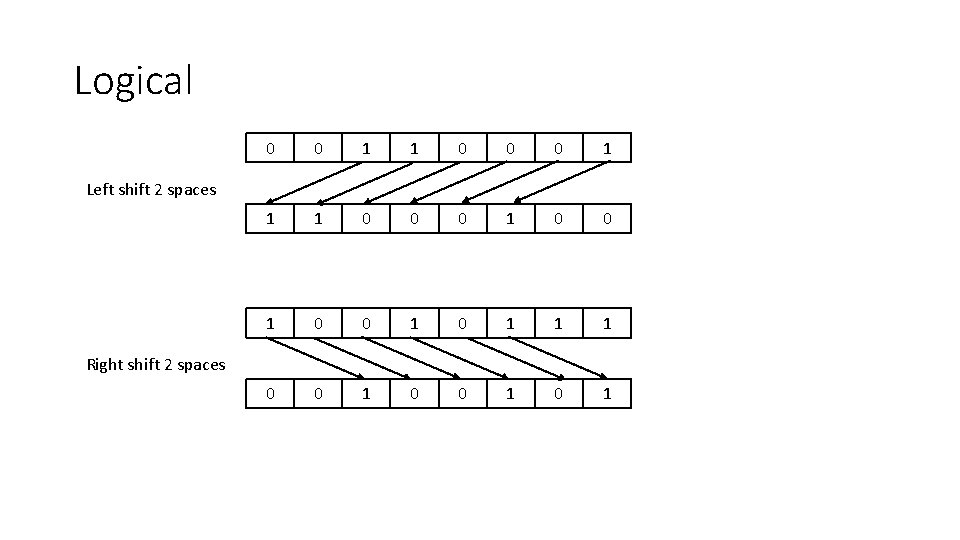
Logical 0 0 1 1 0 0 0 1 0 1 1 1 0 0 1 0 1 Left shift 2 spaces Right shift 2 spaces
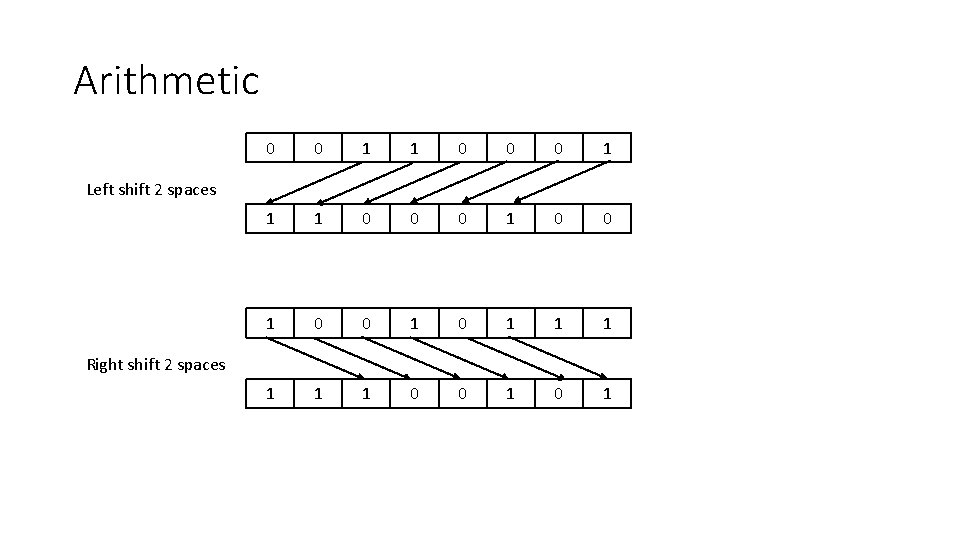
Arithmetic 0 0 1 1 0 0 0 1 0 1 1 1 0 0 1 Left shift 2 spaces Right shift 2 spaces

What do they do? • Each left shift (log/ari) multiplies the number by 2 • Each logical right shift divides the number by 2 • Each arithmetic right shift divides the number by 2 but keeps the sign (positive/negative for two’s complement) (Arithmetic left shift will keep the sign if bits are not removed)
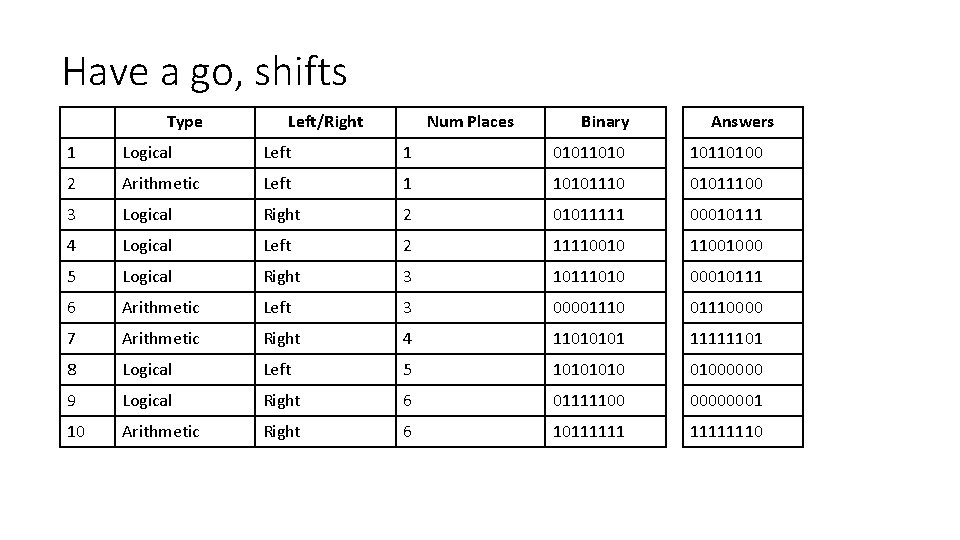
Have a go, shifts Type Left/Right Num Places Binary Answers 1 Logical Left 1 010110100 2 Arithmetic Left 1 101011100 3 Logical Right 2 01011111 00010111 4 Logical Left 2 1111001000 5 Logical Right 3 10111010 00010111 6 Arithmetic Left 3 00001110000 7 Arithmetic Right 4 11010101 11111101 8 Logical Left 5 1010 01000000 9 Logical Right 6 01111100 00000001 10 Arithmetic Right 6 1011111110
- Slides: 34