Data Representation Hexadecimal Although computers work in binary

Data Representation Hexadecimal Ø Although computers work in binary it is sometimes inconvenient for humans to read everything in Binary. For example in main memory for a 32 bit computer you can have up to 32 bits of memory addresses e. g 01010111000011110101000101111101 Ø To make it easier to read large numbers in binary, they are commonly put into group of four bits and displayed using the Hexadecimal number system. This is essentially base 16. Look at the following number conversion table

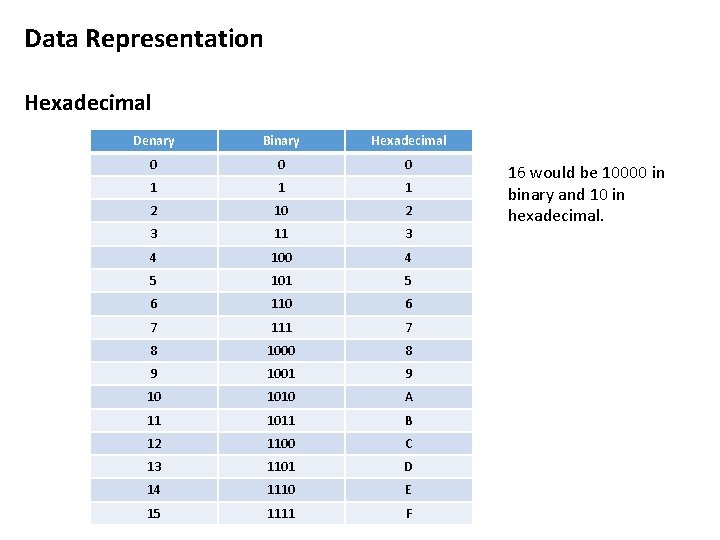
Data Representation Hexadecimal Denary Binary Hexadecimal 0 0 0 1 1 1 2 10 2 3 11 3 4 100 4 5 101 5 6 110 6 7 111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F 16 would be 10000 in binary and 10 in hexadecimal.

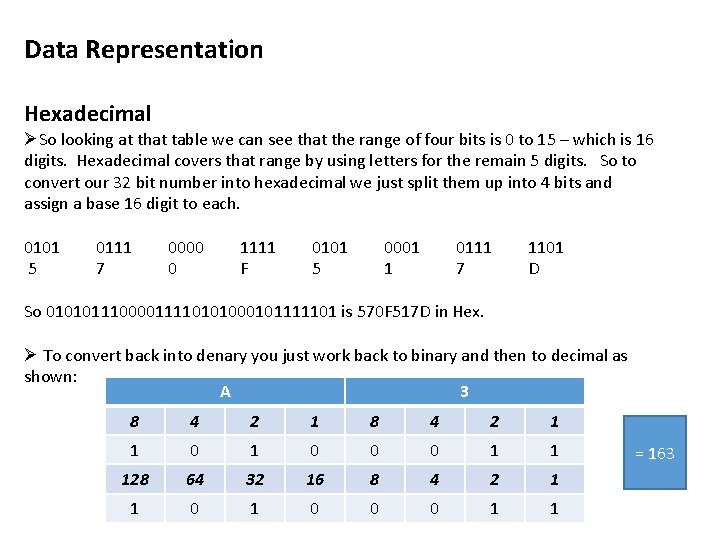
Data Representation Hexadecimal ØSo looking at that table we can see that the range of four bits is 0 to 15 – which is 16 digits. Hexadecimal covers that range by using letters for the remain 5 digits. So to convert our 32 bit number into hexadecimal we just split them up into 4 bits and assign a base 16 digit to each. 0101 5 0111 7 0000 0 1111 F 0101 5 0001 1 0111 7 1101 D So 01010111000011110101000101111101 is 570 F 517 D in Hex. Ø To convert back into denary you just work back to binary and then to decimal as shown: A 3 8 4 2 1 1 0 0 0 1 1 128 64 32 16 8 4 2 1 1 0 0 0 1 1 = 163

Data Representation Exercise 1. Convert the denary number 126 into a) Binary b) Hexadecimal 2. Convert the binary number 0110 1101 into a) Denary b) Hexadecimal 3. Convert the following binary patterns into hexadecimal numbers: 1111 1110 1101 1010 1101. What is the message? SHOW ALL YOUR WORKINGS.