DATA REPRESENTATION Digital computers store information in binary

DATA REPRESENTATION Digital computers store information in binary Binary allows two states * On yes true 1 * Off no false 0 Each digit in a binary number is called a bit 0 1 1 0 bit 0 ff 0 n 0 n 0 ff Binary number system == how numbers can be processed in binary 3/5/2021 CAP 221 1

Binary Numbers • Digits are 1 and 0 – 1 = true – 0 = false • MSB – most significant bit • LSB – least significant bit • Bit numbering: 3/5/2021 CAP 221 2

Number system • A number system of base (radix) r is a system that uses distinct symbol for r digits. • Numbers are represented by a string of digit symbols. 3/5/2021 CAP 221 3

Number system • The base of a number is usually specified as a subscript, e. g. : 1. (01000011)2, 2. (71203)8, 3. (FF 078 ABC)16, . . . etc. • Or a letter indicating the base (d for decimal, b for binary, o for octal and h for hexadecimal) is appended to the number, e. g. : 1. 01000011 b, 2. 71203 o, 3. FF 078 ABCh, . . . etc. 3/5/2021 CAP 221 4

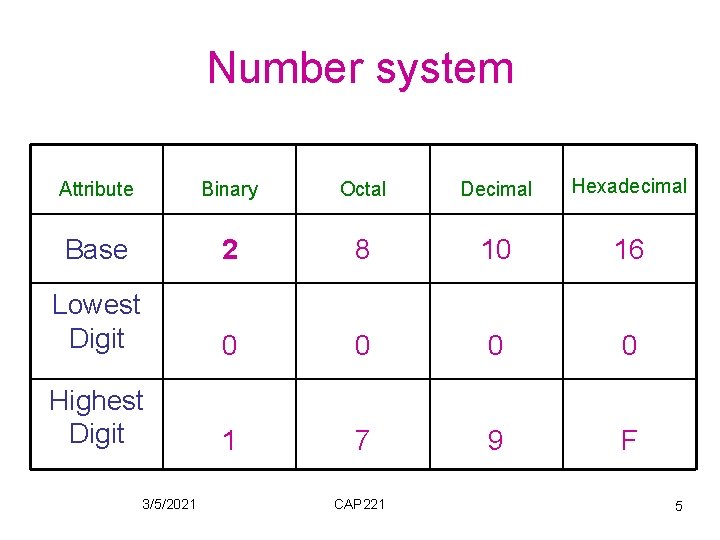
Number system Attribute Binary Octal Decimal Hexadecimal Base 2 8 10 16 Lowest Digit 0 0 Highest Digit 1 7 9 F 3/5/2021 CAP 221 5

Number system • The value of a digit depends not only on its value but also on its position within the number → gives the power of the radix by which it is multiplied. 3/5/2021 CAP 221 6

Positional values in the decimal number system Decimal Digit 9 3 7 Position Name Hundreds Tens Ones Positional Value 100 10 1 102 101 100 Positional Value as a power of the base (10) 3/5/2021 CAP 221 7

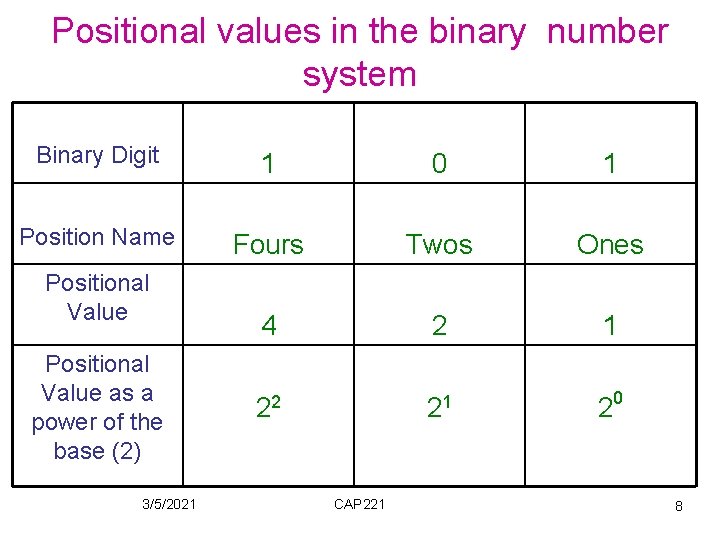
Positional values in the binary number system Binary Digit 1 0 1 Position Name Fours Twos Ones 4 2 1 22 21 0 Positional Value as a power of the base (2) 3/5/2021 CAP 221 2 8

Example 2 0 1 -1 -2 • 379. 25= 3*10 + 7*10 + 9*10+2*10+5*10 n n-1 • (dndn-1. . . d 0. f 1 f 2…fm)r = dn* ( r ) + dn-1* ( r ) +…. + 0 -1 -2 -m d 0* ( r ) + f 1* ( r ) + f 2* ( r ) +…+ fm* ( r ) Converting to decimal 3/5/2021 CAP 221 9

Examples on converting from different bases to Decimal Convert the following to Decimal: • (1001001)2 • (203)8 • (FA 07)16 Solution: • (1001001)2 = 1 + 0*22 + 1*23 + 0*24 + 0*25 + 1*26 = 73 d • (203)8 = 3 + 0*81 + 2*82 = 131 d • (FA 07)16 = 7 + 0*161 + 10*162 + 15*163 = 64007 d 3/5/2021 CAP 221 10

Conversion from decimal • The conversion of a decimal integer into a base r is done by: – Whole numbers: divisions by r – Fractions: repeated multiplication by r. 3/5/2021 CAP 221 11

Conversion from decimal To convert from decimal to any numbering system with base r : • The decimal number is divided by r, • Keeping the remainder aside, the result is further divided by r, and the new remainder is kept aside, • The new result is divided again by r, and so on till the result is less than r and this would be the last remainder, • The remainders make up the equivalent base-r number, with the last remainder being the most-significant digit and the first remainder being the least-significant digit. 3/5/2021 CAP 221 12

Conversion to binary Whole number • Ex. : (67)10 = (? )2 2 67 2 33 rem 2 16 rem 2 8 rem 2 4 rem 2 2 rem 2 1 rem 0 rem 3/5/2021 1 LSB 1 0 0 1 MSB CAP 221 67 d= 10000112 13

Fraction Repeat multiplication by 2 until the fractional product is 0 Ex. : (0. 3125)10 = (? )2 Carry 0. 3125* 2 = 0. 625 0 MSB 0. 625* 2 = 1. 25 1 (0. 3125)10= (0. 0101)2 0. 25* 2 = 0. 5 0 0. 5* 2 = 1. 00 1 LSB 3/5/2021 CAP 221 14

Conversion to base r (50) 10 = (? )8 8 50 6 2 0 6 3/5/2021 (50)10 = (62)8 CAP 221 15

Octal and Hexadecimal number systems –Binary numbers are long. –On average, it takes about 3. 3 times as many digits to represent a value in binary as it does to represent the same value in decimal. 3/5/2021 CAP 221 16

Octal and Hexadecimal number systems If a base R 1 is an integral power of d another base R 2 i. e. R 1= R 2 → Group of d digits in base R 2 maps directly into one digit in base R 1 And each digit in base R 1 maps directly into d digits in base R 2. 3/5/2021 CAP 221 17

Octal number systems 3 Base = 8 = 2 → d = 3 Digits: 0 → 7 Binary to Octal conversion: Group every 3 bits (starting from the right) Replace them by their corresponding octal digit Ex. : ( 0 1 1 0 1 )2 = ( 265 )8 ( 1 0 0 0 1 )2 = ( 21 )8 3/5/2021 CAP 221 18

Octal to binary conversion – Replace each digit by its 3 -bit binary equivalent. – Ex. : (476)8 = (100111110)2 3/5/2021 CAP 221 19

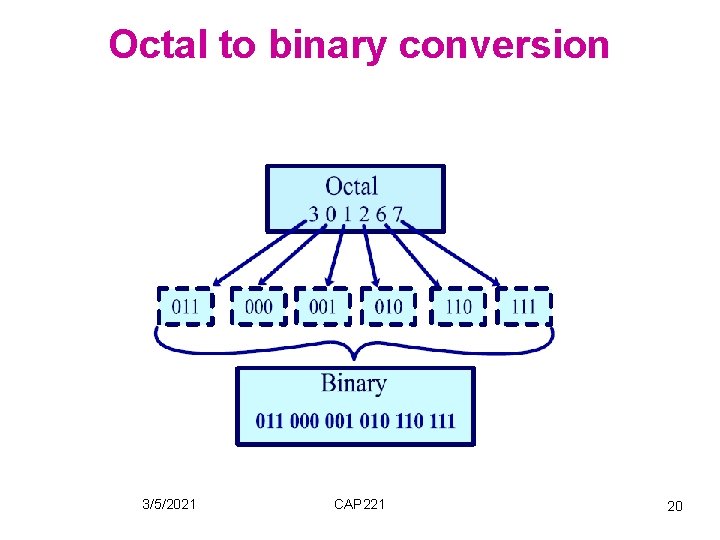
Octal to binary conversion 3/5/2021 CAP 221 20

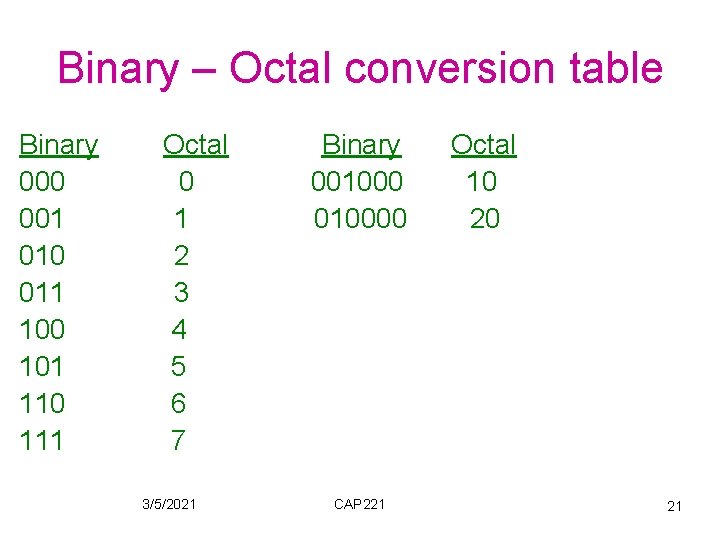
Binary – Octal conversion table Binary 000 001 010 011 100 101 110 111 Octal 0 1 2 3 4 5 6 7 3/5/2021 Binary 0010000 CAP 221 Octal 10 20 21

Hexadecimal number systems (Hex) 4 Base = 16 = 2 → d = 4 Digits: 0, 1, 2, …. . , 9, A, B, C, D, E, F Where A = 10, B = 11, C = 12, D = 13, E = 14, F = 15 3/5/2021 CAP 221 22

Binary to Hex conversion Group each 4 bits and replace them by their corresponding hex digit. Ex. : ( 1 0 1 0 1 )2 = ( B 5 )16 3/5/2021 CAP 221 23

Hex to binary conversion Replace each digit by their 4 bit binary equivalent Ex. : ( 1 D 9 C )16 = (0001110110011100 )2 3/5/2021 CAP 221 24

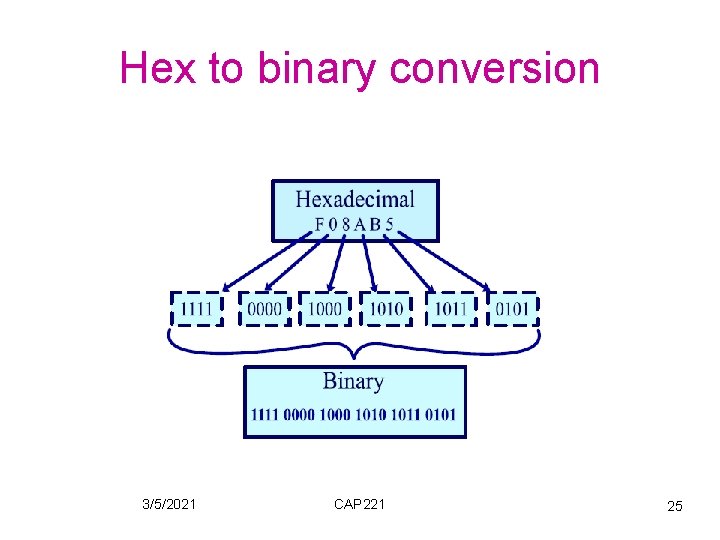
Hex to binary conversion 3/5/2021 CAP 221 25

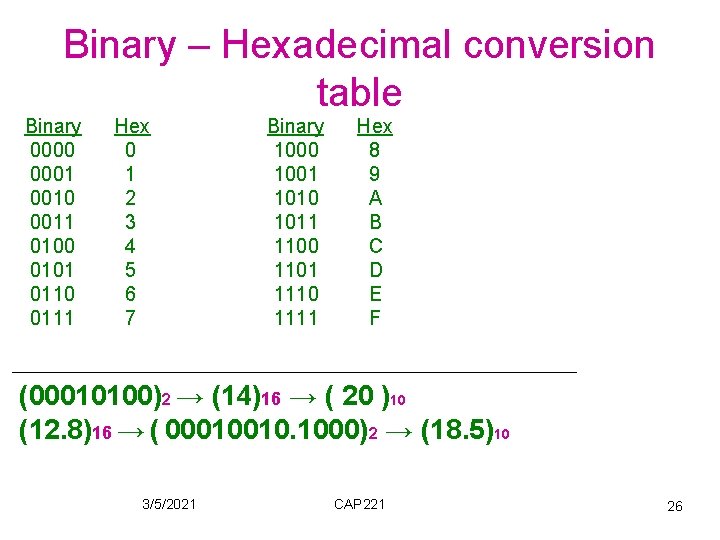
Binary – Hexadecimal conversion table Binary 0000 0001 0010 0011 0100 0101 0110 0111 Hex 0 1 2 3 4 5 6 7 Binary 1000 1001 1010 1011 1100 1101 1110 1111 Hex 8 9 A B C D E F (00010100)2 → (14)16 → ( 20 )10 (12. 8)16 → ( 00010010. 1000)2 → (18. 5)10 3/5/2021 CAP 221 26

Binary Arithmetic operations • Addition 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 10 (carry) 3/5/2021 CAP 221 27

Binary Arithmetic operations • Subtraction 0 -0=0 0 - 1 = 1 (after borrowing) 1 -0=1 1 -1=0 3/5/2021 CAP 221 28

Binary Arithmetic operations • Multiplication 0*0 = 0 0*1 = 0 1*0 = 0 1*1 = 1 3/5/2021 CAP 221 29

ADDITION • Like decimal numbers, two numbers can be added by adding each pair of digits together with carry propagation. 3/5/2021 CAP 221 30

Example Carries 3/5/2021 CAP 221 31

SUBTRACTION • Two numbers can be subtracted by subtracting each pair of digits together with borrowing, where needed. 3/5/2021 CAP 221 32

SUBTRACTION 3/5/2021 CAP 221 33

Representation of signed binary numbers • Given a fixed number of bit positions (n), we n can represent 2 patterns: From (00. . 0)2 to (11. . 1)2. • Using unsigned numbers we can represent n 0 → 2 -1 n • Using signed numbers → 2 positive & negative patterns 3/5/2021 CAP 221 34

Complementary notations • The most commonly used way of representing signed numbers. It greatly simplifies all arithmetic operations. • Positive number is represented as it is (like an unsigned positive number). • Negative numbers are represented by the complement of unsigned number. 3/5/2021 CAP 221 35

Complementary notations • The value used for complementation is a power of the base or less one than a power of the base. • For binary numbers: we have 2’s complement and 1’s complement. • For decimals, we have 10’s complement and 9’s complement. • For hex. Numbers we have 16’s complement and F’s (15’s) complement. 3/5/2021 CAP 221 36

One’s complement • Is obtained by subtracting the number from (11. . 1)2 (n 1’s) → reversing each bit: changing every 1 to 0 and every 0 to 1. • Ex. : represent +(14 d), -(14 d) in 8 -bit binary number • (+14)10 = ( 00001110)2 = (00001110)1 s • (-14)10 = -( 00001110)2 = (11110001)1 s 3/5/2021 CAP 221 37

For 8 -bits number system: • Largest positive number: 0 1111111 = +(127)10 • smallest negative number: 1 0000000 = - (127)10 • Zeroes: 0 0000000 1 1111111 • Range: m-1 - (2 -1) to + 2 -1 (m : the number of bits) • -(127)10 to +(127)10 • The most significant bit represents the sign: 0 = +ve ; 1 = -ve. 3/5/2021 CAP 221 38

2’s complement • Take the 1’s complement and add 1 → invert all the bits and add 1. • Ex. : 2’s complement of (01110100)2: 1’s complement = (10001011)2 add 1 → 2’s complement = (10001100)2 3/5/2021 CAP 221 39

2’s complement • 2’s complement of (0000)2: 1’s complement = (1111)2 add 1 → (10000)2 • 2’s complement of n-bit number include only the rightmost n bits: 2’s complement of (0000)2 = (0000)2 3/5/2021 CAP 221 40

2’s complement - For 8 -bit binary numbers 2’s complement of (5)d = (00000101)2: 1’s complement = (11111010)2 add 1→ (11111011)2 510 + (-5)10 → 000001012 + 111110112 = 100002 Carry 2’s complement of any N integer represents –N: N + (-N) = 0 3/5/2021 CAP 221 41

2’s complement • To find the 2’s complement of a binary number, proceeding from right to left, leave all bits unchanged up to and including the first `1`. Reverse all the remaining bits. • Range of signed value that can be represented in 2’s complemented notation is m-1 - 2 to 2 -1 3/5/2021 CAP 221 42

For 8 -bits number system: • Largest positive number: 0 1111111 = +(127)10 • smallest negative number: 1 0000000 = - (128)10 • Zero: 0 0000000 • Range: -(128)10 to +(127)10 • The most significant bit represents the sign: • 0 = +ve ; 1 = -ve. 3/5/2021 CAP 221 43

2’s complement in hexadecimal • Each group of four bits corresponds to a single hexadecimal digit. • Subtract each hexadecimal digit from F and then add 1 (equivalent of taking the 16’s complement). 3/5/2021 CAP 221 44

Ex. : 2’s complement of (3 A 6 E)16 1’s complement: FFFF - 3 A 6 E C 591 + 1 2’s complement: (C 592)16 3/5/2021 CAP 221 45

Comparing 2’s complement numbers Check the signs: If they differ, they determine the order If they are the same, the order of the numbers is the same as that of their representations. 3/5/2021 CAP 221 46

Ex. : (01001100)2 and (10100101)2 Different signs → the 1 st # is +ve the 2 nd # is –ve → 1 st # > 2 nd # 3/5/2021 CAP 221 47

(10110010)2 and (10111001)2 • Both numbers are negative: 1 st # < 2 nd # 3/5/2021 CAP 221 48

Signed binary arithmetic Overflow • Signed binary numbers are of a fixed range. • If the result of addition/subtraction goes beyond this range, overflow occurs. • Two conditions under which overflow can occur are: (i) positive add positive gives negative (ii) negative add negative gives positive 3/5/2021 CAP 221 49

2 s complement addition Algorithm: • Perform binary addition on the two numbers. • Ignore the carry out of the MSB. • Check for overflow: Overflow occurs if the carriers into and out of the MSB are different. 3/5/2021 CAP 221 50

2 s complement subtraction Algorithm for performing A - B: A-B = A + (-B) • Take 2 s complement of B by inverting all the bits and adding 1 • Add the 2 s complement of B to A 3/5/2021 CAP 221 51

2 s complement addition/Subtraction • Examples (4 -bits system ) : +3 + +4 ---+7 ---- 0011 + 0100 ------0111 ------- 3/5/2021 -2 + -6 ----8 ---- CAP 221 1110 + 1010 ------11000 ------- 52

2 s complement addition/Subtraction +6 + -3 ---+3 ---- 0110 + 1101 ------10011 ------- 3/5/2021 +4 + -7 ----3 ---- CAP 221 0100 +1001 ------1101 ------- 53

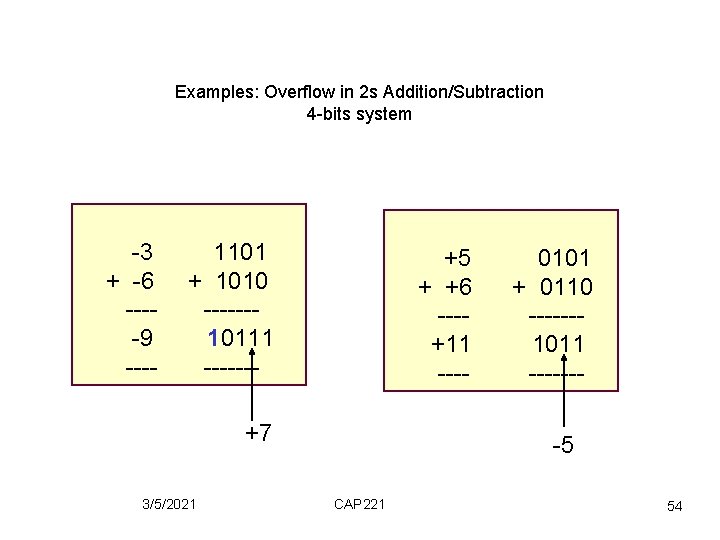
Examples: Overflow in 2 s Addition/Subtraction 4 -bits system -3 + -6 ----9 ---- 1101 + 1010 ------10111 ------- +5 + +6 ---+11 ---- +7 3/5/2021 0101 + 0110 ------1011 -------5 CAP 221 54

Examples 1)Add 45 and – 18 (use 8 -bit 2`s complement representation (45)d = B`00101101` (18)d = B`00010010` → (-18)d = B`1110` B`00101101` +B`1110` B`100011011` → +27 Discard carry 3/5/2021 CAP 221 55

Examples 2)Add 38 and – 57 38= B`00100110` 57=B`00111001` → -57= B`11000111` B` 00100110` + B `11000111` = B`11101101` → -19 3/5/2021 CAP 221 56

Examples 3)Add 110 and 75 110 + 75 = 185 010011100 carries 110= B`01101110` 75=B`01001011` + B`01001011` B`10111001 negative result → overflow: the result is too big. 8 bits → -128< I < 127 3/5/2021 CAP 221 57

Examples 4)Subtraction: B`01101011` -B`00101001` 2’s complement of B`00101001` is `11010111` B`01101011` + B`11010111` = B`101000010` 3/5/2021 CAP 221 58

Examples • Note: In addition & subtraction, if the operands have different length, the shortest must be sign extended. • Ex. 1) Add B`1011` with B`01101101` B`11111011` + B`01101101` = B`101101000` 3/5/2021 CAP 221 59

Examples 2) subtract X`A 3 BC` from X`34 A 10 BEE` X`A 3 BC` sign extended → FFFFA 3 BC 2’s complement → FFFF-FFFFA 3 BC +1 = 00005 C 44 X`34 A 10 BEE` + X`00005 C 44` = X`34 A 16832 3/5/2021 CAP 221 60

CODING • The most fundamental problem of coding is to get as much information as possible in a fixed-length representation. • In binary: How many different binary numbers we can write with n bits for a fixed n n? → 2 numbers. 3/5/2021 CAP 221 61

Binary Coded Decimal (BCD) • • Decimal numbers are more natural to humans. Binary numbers are natural to computers. Quite expensive to convert between the two. If little calculation is involved, we can use some coding schemes for decimal numbers. 3/5/2021 CAP 221 62

Binary Coded Decimal (BCD) • • One such scheme is BCD, also known as the 8421 code. Represent each decimal digit as a 4 -bit binary code. 3/5/2021 CAP 221 63

Binary Coded Decimal (BCD) • Some codes are unused, eg: (1010)BCD, (1011)BCD, …, (1111)BCD. These codes are considered as errors. • Easy to convert, but arithmetic operations are more complicated. 3/5/2021 CAP 221 64

Binary Coded Decimal (BCD) • Examples: (234)10 = (0010 0011 0100)BCD (7093)10 = (0111 0000 1001 0011)BCD (1000 0110)BCD = (86)10 (1001 0100 0111 0010)BCD = (9472)10 Note: • BCD is not equivalent to binary. • Example: (234)10 = (11101010)2 3/5/2021 CAP 221 65

Character data type • Apart from numbers, computers also handle textual data. • Internally all computers represent characters by storing them as binary data • Character set frequently used includes: alphabets: ‘A’. . ‘Z’, and ‘a’. . ‘z’ digits: ‘ 0’. . ‘ 9’ special symbols: ‘$’, ‘, ’, ‘@’, ‘*’, … non-printable: line feed, bell, … 3/5/2021 CAP 221 66

Character data type • Usually, these characters can be represented using 7 or 8 bits. • Two important issues concerning the character codes: - The size i. e. the # of bits used to represent each character. - The collating sequence. 3/5/2021 CAP 221 67

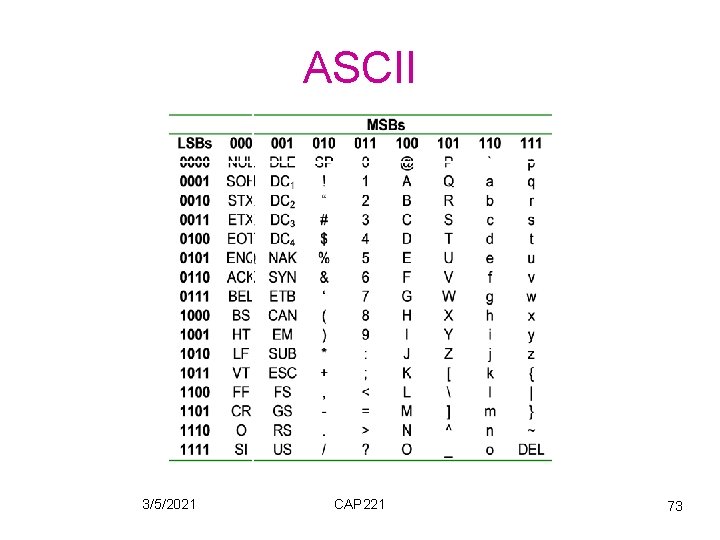
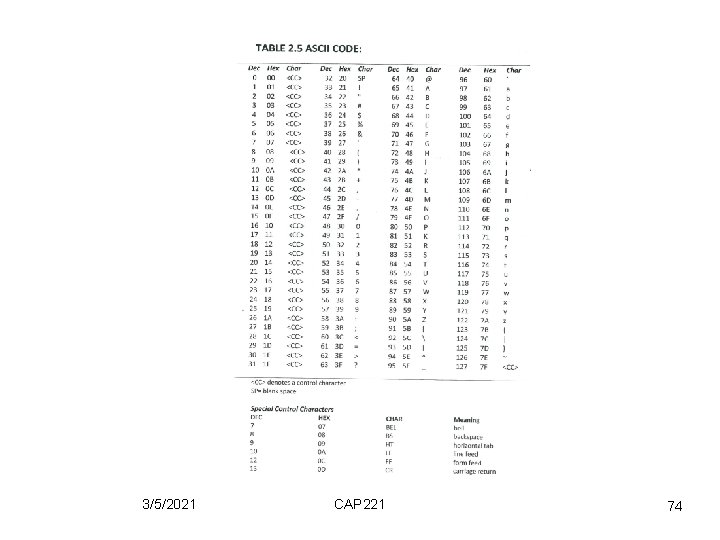
Character data type • Standard encoding of character data is 8 -bit. • Each character was to be represented as a string of 8 -binary digits and there a total 8 of 2 (256) unique characters available. • widely used standard: ASCII (American Standard Code for Information Interchange); 7 -bit the code fits into a byte, with the most significant bit set to 0 3/5/2021 CAP 221 68

ASCII • ASCII code is really 7 -bit code → 128 ASCII codes • 2 calsses of characters: - Printable characters ( code 2016 (408)→ 7 E 16 (1768) ) displayed on screen, or printed on printer. They consist of: . Special characters e. g. $, #, %, <, >, =. Numbers: 0─9. Uppercase characters: A ─ Z. Lowercase characters: a ─ z 3/5/2021 CAP 221 69

ASCII • Control characters: (0 ─ 1 F 16 (378) , 7 F 16 (1778) ). These do not cause a character to be printed but instead initiate some action, control the operation of devices (e. g. tab, LF, CR, ring bell) or convey some status information. 3/5/2021 CAP 221 70

ASCII Example • What is the internal ASCII code for the character string `123`? `1` `2` `3` 0618 0628 0638 3116 3216 3316 00110001 00110010 0011 → 0011000100100011 3/5/2021 CAP 221 71

ASCII • This example points up that the representation of the character string `123` is quit different from the representation of the signed integer +123. • Note: The character representation takes 24 bits (3*8). • The signed integer representation in 16 -bits is: (000001111011)2 3/5/2021 CAP 221 72

ASCII 3/5/2021 CAP 221 73

3/5/2021 CAP 221 74