Data Representation 2 C Programming From Problem Analysis

Data Representation 2 C# Programming: From Problem Analysis to Program Design 4 th Edition 1

Data Representation • Bits – Bit – "Binary dig. IT" – Binary digit can hold 0 or 1 – 1 and 0 correspond to on and off, respectively • Bytes – Combination of 8 bits – Represent one character, such as the letter A – To represent data, computers use the base-2 number system, or binary number system C# Programming: From Problem Analysis to Program Design 2

Binary Number System Figure 2 -1 Base-10 positional notation of 1326 C# Programming: From Problem Analysis to Program Design 3

Binary Number System (continued) Figure 2 -2 Decimal equivalent of 01101001 C# Programming: From Problem Analysis to Program Design 4

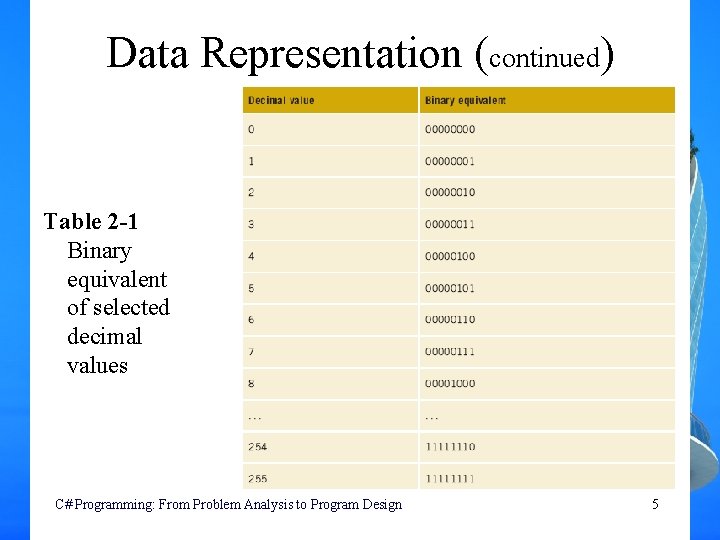
Data Representation (continued) Table 2 -1 Binary equivalent of selected decimal values C# Programming: From Problem Analysis to Program Design 5

Data Representation (continued) • Character sets – With only 8 bits, can represent 28, or 256, different decimal values ranging from 0 to 255; this is 256 different characters • Unicode – character set used by C# (pronounced C Sharp) – Uses 16 bits to represent characters – 216, or 65, 536 unique characters, can be represented • American Standard Code for Information Interchange (ASCII) – subset of Unicode – First 128 characters are the same C# Programming: From Problem Analysis to Program Design 6

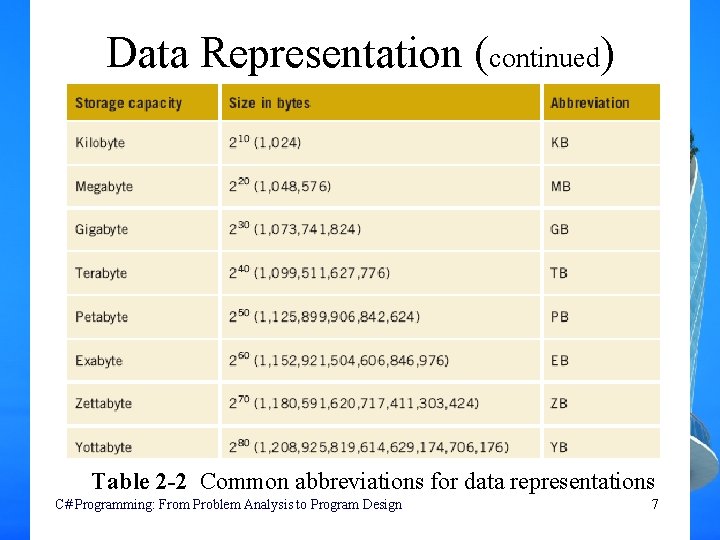
Data Representation (continued) Table 2 -2 Common abbreviations for data representations C# Programming: From Problem Analysis to Program Design 7

Counting to 15 • Binary numbers are usually written in groups of 4, 8 or 16 digits. • 0000 0000

Counting always starts with zero • • 0000 - 0 0001 - 1 0010 - 2 0011 - 3 0100 - 4 0101 - 5 0110 - 6 0111 - 7 • 1000 - 8 • 1001 - 9 • 1010 - 10 • 1011 - 11 • 1100 - 12 • 1101 - 13 • 1110 - 14 • 0111 - 15

Converting Binary to Decimal

Problem Convert the binary number 1011 to a decimal number. Write the binary number on paper 8 4 2 1 x x 1 0 1 1 8 + 0 +2 + 1 = 11

Problem Convert the binary number 101011 to a decimal number. Write the binary number on paper 32 16 8 4 2 1 x x 0 1 x x x 0 1 1 32 + 0 + 8 + 0 +2 + 1 = 43

Binary ‒to‒ Decimal Process The Process : Weighted Multiplication a) Multiply each bit of the Binary Number by it corresponding bitweighting factor (i. e. Bit-0→ 20=1; Bit-1→ 21=2; Bit-2→ 22=4; etc). b) Sum up all the products in step (a) to get the Decimal Number. Example: Convert the decimal number 01102 into its decimal equivalent. 0 1 1 0 23 22 21 20 8 4 2 1 0 + 4 + 2 + 0 Bit-Weighting Factors = 0110 2 = 6 10 610 13

Binary → Dec : Example #1 Example: Convert the binary number 100102 into its decimal equivalent. 14

Binary → Dec : Example #1 Example: Convert the binary number 100102 into its decimal equivalent. Solution: 100102 = 1810 15

Binary → Dec : Example #2 Example: Convert the binary number 01101012 into its decimal equivalent. 16

Binary → Dec : Example #2 Example: Convert the binary number 01101012 into its decimal equivalent. Solution: 01101012 = 5310 17

Binary → Dec : More Examples a) 0110 2 = ? 6 10 b) 11010 2 = ? 26 10 c) 0110101 2 = ? 53 10 d) 11010011 2 = ? 211 10 18

Octal base 8 counting 000 – 0 001 – 1 002 – 2 003 – 3 004 – 4 005 – 5 006 – 6 007 – 7 010 – 8 011 – 9 012 – 10 013 – 11 014 – 12 015 – 13 016 – 14 017 – 15 020 – 16

Octal to Decimal – Base 8

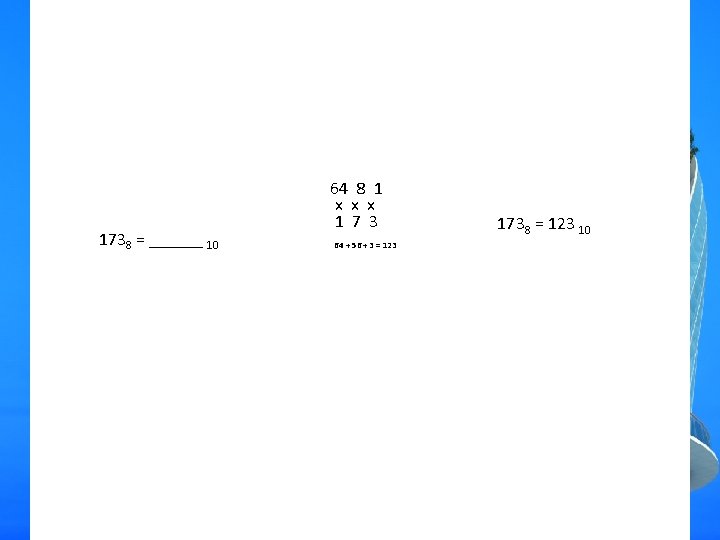
1738 = ______ 10 64 8 1 x x x 1 7 3 64 + 56 + 3 = 123 1738 = 123 10